含电动汽车智慧楼宇的多时间尺度MPC能量管理策略

2023-03-14姜晓锋王永灿贾世成杨健维

重庆理工大学学报(自然科学) 2023年2期

姜晓锋，魏巍，王永灿，徐琳，刘畅，贾世成，杨健维

(1.国网四川省电力公司电力科学研究院，成都 610041；2.西南交通大学电气工程学院，成都 611756)

0 引言

近年来，全球能源需求快速增长、城市化进程加快，楼宇能耗占比正逐步攀升。因此，有必要研究提高智慧楼宇能源利用效率的能量管理策略[1-2]。同时，随着电动汽车大规模普及，智慧楼宇建设充电桩是大势所趋。然而，电动汽车的出行及充电行为具有强随机性[3-5]，给智慧楼宇的能量管理带来了新的挑战。因此，亟需寻找一种适用于含电动汽车智慧楼宇的能量管理策略，以在满足电动汽车充电需求的同时，帮助智慧楼宇更加节能、经济、高效地运行。

目前，国内外学者针对智慧楼宇的能量管理策略开展了一定研究。文献[6-8]采用日前优化调度方案对楼宇进行能量优化管理。其中，文献[6]采用混合整数非线性规划方法求解了楼宇能量管理的最优调度问题。文献[7]基于离散二进制粒子群算法解决了智能楼宇的光伏与储能调度问题。文献[8]基于灰狼优化算法解决了商业楼宇的能量分配问题。然而，上述研究均采用的是单一时间尺度的优化调度策略，难以反映实际运行中楼宇内可再生能源与负荷的出力波动对楼宇能量管理的影响。

多时间尺度能量管理策略通过逐级细化各调度层所采用的时间尺度，提高对可再生能源与负荷出力的预测频率，可有效解决由于日前预测误差所带来的源荷不匹配等问题[9-10]。文献[11]针对商业楼宇，建立了从日前到日内的多时间尺度能量管理策略。文献[12]建立了从短时间到超短时间尺度的联络线功率平滑控制方法。文献[13]建立了从日前离线优化到实时在线决策的楼宇能量管理方法。

上述研究中，日内及实时调度层采用的调度方法均属于开环优化方法，是基于系统单一时间断面信息的优化控制方法，对于系统未来状态变化的感知效果差，难以应对系统状态突变等问题。而模型预测控制(model predictive control,MPC)是一种基于预测模型并在有限时域内进行滚动优化，结合实际数据进行修正的闭环控制方法，可有效解决预测不确定问题，并在应对外界扰动下具有较强鲁棒性。

文献[14]提出将MPC方法应用于智能楼宇的多时间尺度能量管理中，但是该文献并没有考虑将EV作为一种可调度资源参与楼宇的能量管理，也没有挖掘EV出行特性对于楼宇能量管理的影响，因此，没有充分发挥出EV作为一种可调度资源参与楼宇日前调度以及日内修正的调节能力。

基于此，本文在综合考虑EV出行特性的基础上，提出了基于MPC的多时间尺度优化调度方法，并将其应用于含电动汽车智慧楼宇的能量管理中。首先，对EV出行特性进行分析，并利用蒙特卡洛模拟抽取EV到达、离开时刻以及充电始末荷电状态；其次，根据智慧楼宇内各单元的负荷特性，建立其能量管理混合整数二次规划(mixed integer quadratic programming,MIQP)模型，并对模型进行快速求解，形成日前优化调度策略。然后，考虑日内可再生能源与负荷的出力波动，基于系统状态空间预测模型以及短期功率预测方法，建立基于MPC的日内滚动优化调度策略，至此形成从日前全局优化到日内动态修正的多时间尺度能量管理策略；最后，与多种能量管理策略对比，证明所提策略在应对日内可再生能源与负荷出力波动下的优越性。

1 智慧楼宇能量管理系统架构

典型智慧楼宇模型由楼宇主体以及停车场充电站组成，如图1所示。智慧楼宇主要描述上级电网、分布式电源、风机、光伏、储能、EV以及负荷等可调度资源间的能量交换需求，并利用楼宇能量管理系统(building energy management system,BEMS)进行能量优化管理。其中，功率流指经过BEMS决策后各可调度资源与联络线之间的交互功率大小；交通流主要描述EV在到达与离开充电站时间上的随机性；信息流指各种可调度资源的控制信号流。

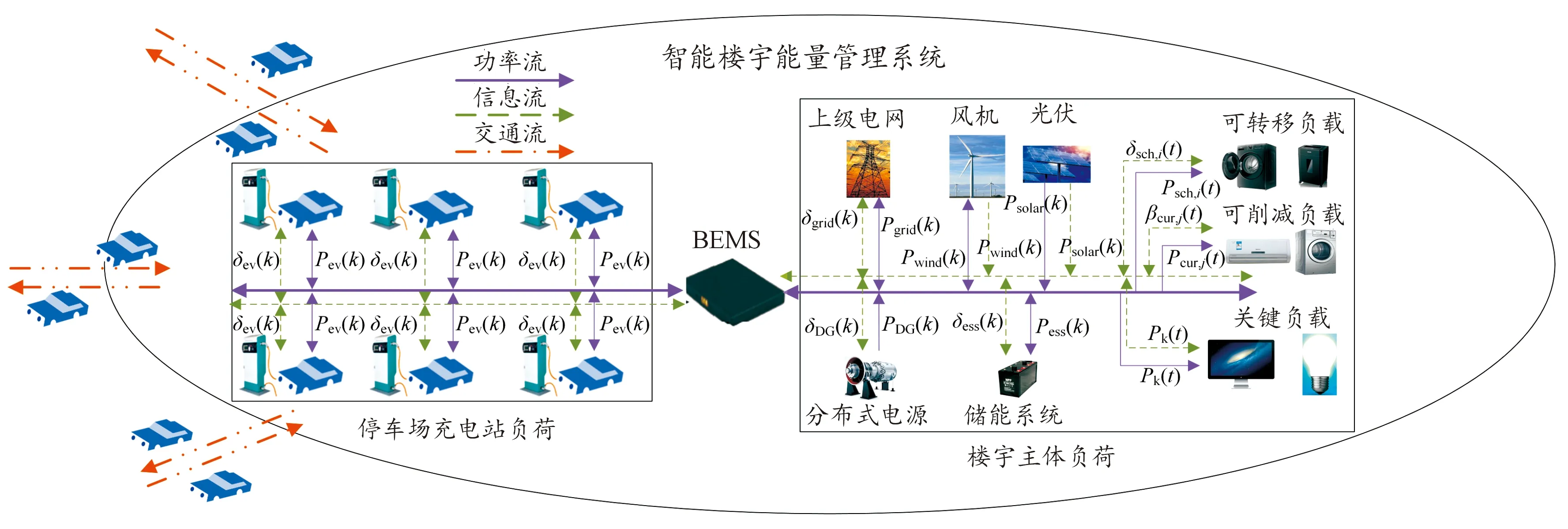
图1 BEMS结构示意图

2 智慧楼宇能量管理模型

智慧楼宇能量管理模型主要是考虑上级电网、楼宇内风机、光伏、智能负载、分布式电源、EV及储能系统等单元工作特性的不同，分别建立其能量管理的MIQP模型。同时，智慧楼宇的能量管理模型需要首先满足楼宇内各时刻的功率平衡约束：

Pgrid(k)+Psolar(k)+Pwind(k)+Pess(k)=

(1)

式中:Pgrid(k)、Psolar(k)、Pwind(k) 、Pess(k)、Pev(k)分别为楼宇向电网购售电的功率、光伏、风机、储能及EV的输出功率；Pk,q(k)、Pcur, j(k)、Psch,i(k)表示k时刻关键负载q、可削减负载j、可转移负载i的功率；Q、N、M分别为关键负荷、可削减、可转移负荷数量；R为k时刻在网的EV数量。

2.1 分布式电源模型

构建分布式电源(distributed generation,DG)模型，需要考虑DG的输出功率约束、启停时长约束、爬坡功率限制以及启停次数约束[15]，可以表示为：

(2)

2.2 储能模型

构建储能系统的能量管理模型，需要描述储能系统的实时可用容量，并满足其功率约束、容量限制，以及始末荷电状态相等约束[15]，可以表示为：

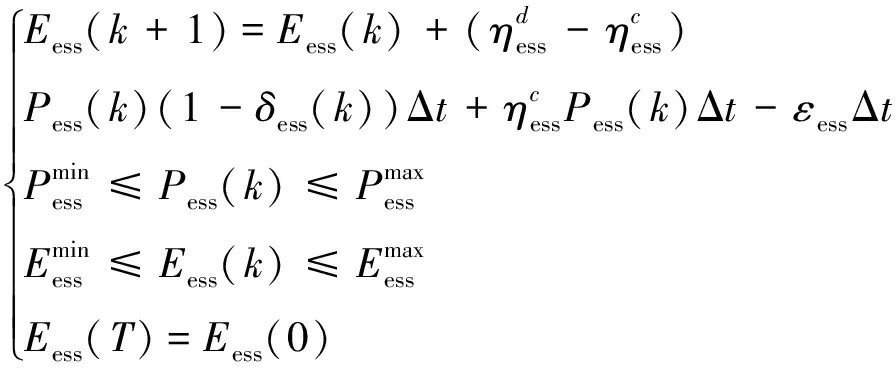
(3)

2.3 电动汽车负荷模型

假设只有停留在楼宇内的EV才能参与楼宇的能量管理，并考虑EV与楼宇间的双向能量交互(V2G)以及EV在到达/离开楼宇时间上的随机性，分别建立单体电动汽车的V2G模型以及EV到达/离开时刻的概率分布模型。

2.3.1单体电动汽车的V2G模型

考虑EV与楼宇的双向能量交互(V2G)情况下，EV的能量管理模型与储能相似，只是EV还需要满足其到达与离开时间约束，本文将在2.3.2节对EV的到达/离开时刻进行建模分析。

(4)

2.3.2EV到达/离开时刻概率分布模型

受用户行为影响，EV在到达/离开楼宇的时间上具有一定的随机性及统计规律。因此，为刻画EV的出行规律，本文基于2017年美国家庭旅行调查数据集[16]，采用概率拟合函数的方式刻画EV出行规律，并对EV出行特性进行分析。同时，考虑到EV在不同功能区内出行特性的区别，设计两类典型楼宇(居民、商业)进行对比分析。针对居民楼宇，采用广义极值分布对EV离开居民楼宇时刻进行概率拟合；针对商业楼宇，采取双混合正态分布对EV到达商业楼宇时刻进行概率拟合，两者拟合的结果如图2所示，拟合得到的概率密度函数分别如式(5)(6)所示。

图2 EV到达/离开时间概率拟合结果

(5)

(6)

同时，由文献[16]可知，EV在居民区及商业区停留时长分别服从威布尔分布以及广义极值分布：

(7)

(8)

式中：t为EV在居民楼宇、商业楼宇的停留时长。

2.4 负荷模型

2.4.1可转移负荷

可转移负荷的工作时段可以在一定时间范围内调整，但负荷一旦开始工作就不能中途停止[17]。

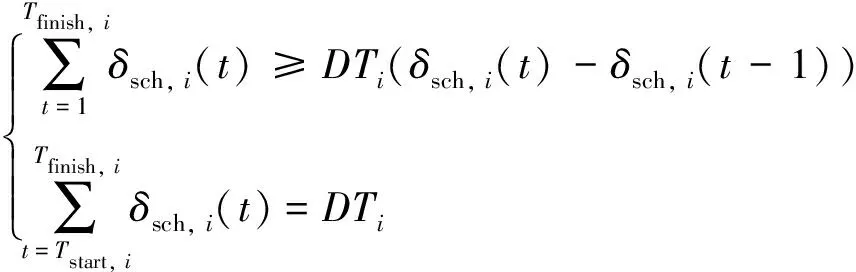
(9)

式中：δsch, i(t)表示负荷i的工作状态；Tstart, i、Tfinish, i、DTi表示负荷i最早开始、最晚结束时间、运行时长。

2.4.2可削减负荷

可削减负荷工作功率在一定范围内可以调整，但在非工作时段需要恢复切除的功率，满足负荷总运行需求[17]，表示为：

(10)

2.4.3关键负荷

关键负荷对供电可靠性要求较高，为了满足居民基本生活需求，关键负荷只能以额定功率运行[17]。

(11)

式中：Pk(t)表示为关键负荷k在t时刻的运行功率。

2.5 楼宇与电网能量交互模型

构建楼宇与电网能量交互模型，考虑楼宇在能量不足时向电网购电，并在能量盈余时向电网售电。

(12)

(13)

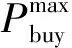
3 基于MPC多时间尺度能量管理策略

针对含电动汽车智慧楼宇的能量管理，提出一种基于MPC的多时间尺度能量管理策略。首先，日前优化调度策略考虑EV的出行特性，求解出每个时刻可参与楼宇能量管理的EV数量，并通过对楼宇能量管理的MIQP模型进行快速求解，得到设备未来一日的出力计划；随后日内优化调度策略以日前计划为参考，针对日内可再生能源及负荷的出力波动，采用基于MPC的滚动优化方法，对日前计划进行动态修正，形成多时间尺度能量管理策略，其流程如图3所示。

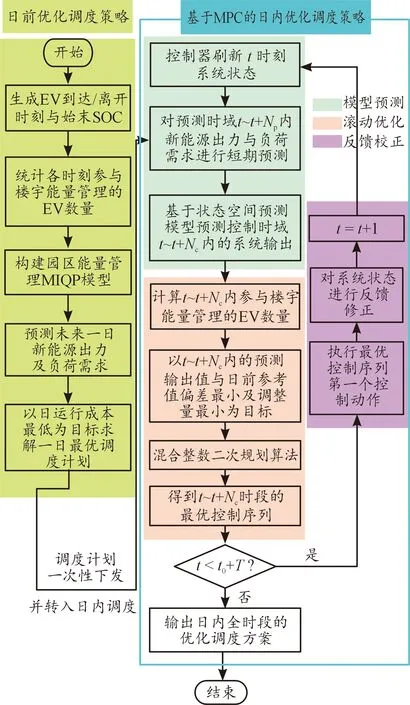
图3 多时间尺度能量管理流程框图

如图3所示，日前调度层通过预测未来一日的可再生能源出力及负荷需求，一次性求解未来24 h的最优调度方案，并全部下发给日内调度层。日内调度层在接收到日前调度计划后，以日前调度计划作为参考，循环执行模型预测、滚动优化和反馈校正3个步骤，以进行对日前计划的动态修正。在日内优化调度结束后，输出全时段优化调度方案。

3.1 日前优化调度策略

楼宇能量管理日前调度以楼宇一日运行成本最低为目标，包括DG、储能、EV的运行维护费用、购/售电成本、电网对可转移、可削减负荷的补偿以及新能源机组运行成本[15]，其表达式如下：

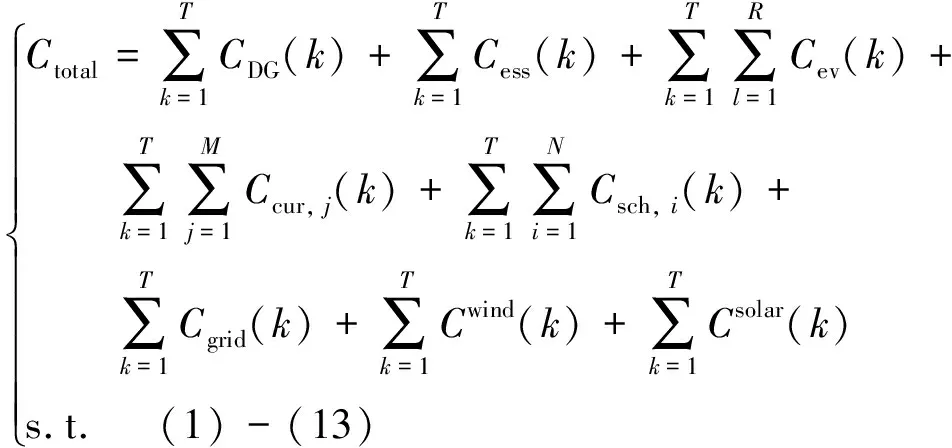
(14)

式中：CDG(k)、Cess(k)、Cev(k)表示DG、储能及EV运行维护费用；Cgrid(k)表示购/售电费用；Csch, i(k)、Ccur, j(k)表示用户对可转移负荷工作时间转移以及可削减负荷功率切除的不满意费用(即电网提供的补偿)；Csolar(k)、Cwind(k)表示光伏、风机运行成本。

利用混合逻辑动态建模方法将目标函数转换为混合整数二次规划，得到各项成本表示如下：

CDG(k)=CFuel(P(k))+CSU(k)

(15)

CFuel(P(k))=aP2(k)+bP(k)+c

(16)

CSU(k)=CDGupmax(0,δDG(k)-δDG(k-1))

(17)

(18)

(19)

(20)

Csch, i(k)=Psch, iτi(k)χsch, i(k)Δt

(21)

(22)

Cgrid(k)=(ρbuy-ρsell)Cg(k)zgrid(k)Δt+

ρsellCg(k)Pgrid(k)Δt

(23)

zgrid(k)=δgrid(k)Pgrid(k)

(24)

Csolar(k)=ρsolarCg(k)Psolar(k)Δt

(25)

Cwind(k)=ρwindCg(k)Pwind(k)Δt

(26)

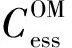
3.2 基于MPC的日内滚动优化调度策略

模型预测控制本质上是一种基于模型的有限时域闭环最优控制算法，主要包含预测模型、滚动优化、反馈校正3个步骤。本文基于MPC算法流程，设计智慧楼宇日内滚动优化调度策略如下。

3.2.1预测模型

基于状态空间预测方程，建立了如式(27)所示的楼宇能量管理预测模型。

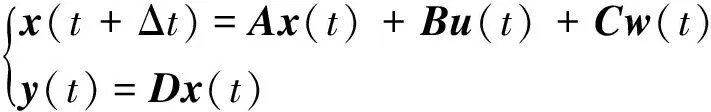
(27)

式中：x(t)表示能量管理的状态向量，其由t时刻EV充/放电功率Pev(t)、DG出力PDG(t)、储能充/放电功率Pess(t)、购/售电功率Pgrid(t)、储能荷电状态Sess(t)、EV荷电状态Sev(t)构成，见式(28)；u(t)为能量管理的控制向量，由DG、储能及EV的出力增量ΔPDG(t)、ΔPess(t)、ΔPev(t)组成，见式(29)；w(t)为扰动输入向量，由负荷、风机以及光伏出力短期预测功率增量ΔPload(t)、ΔPwind(t)和ΔPsolar(t)构成，见式(30)；y(t)为输出向量，由Pgrid(t)、Sess(t)、Sev(t)构成，见式(31)。A,B,C,D为状态空间矩阵。

x(t)=[Pev(t),PDG(t),Pess(t),Pgrid(t),Sess(t),Sev(t)]T

(28)

u(t)=[ΔPDG(t) ΔPess(t) ΔPev(t)]T

(29)

w(t)=[ΔPload(t) ΔPwind(t) ΔPsolar(t)]T

(30)

y(t)=[Pgrid(t)Sess(t)Sev(t)]T

(31)

3.2.2滚动优化模型

为减少由于日前预测误差导致的联络线功率波动，确保储能及EV在实际运行中发挥其“削峰填谷”效果，考虑日内设备出力调整成本，以每个控制时域内联络线功率、EV及储能SOC的日内输出值与日前计划值间的偏差最小为目标。建立智慧楼宇日内滚动优化调度模型如式(32)所示。

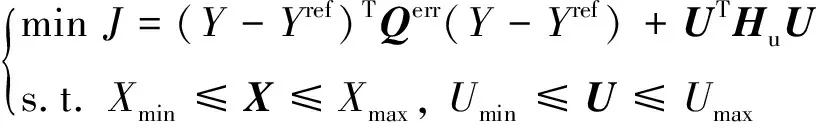
(32)

式中：Y为基于短期预测功率及状态空间预测模型，求解得到的日内输出值，见式(33)；Yref为当前控制时域内的日前计划值，见式(34)；X和U分别为状态向量与控制向量；Qerr为联络线功率、EV及储能SOC跟踪误差的惩罚系数矩阵；Hu为DG、储能及EV出力调整量的成本系数矩阵。

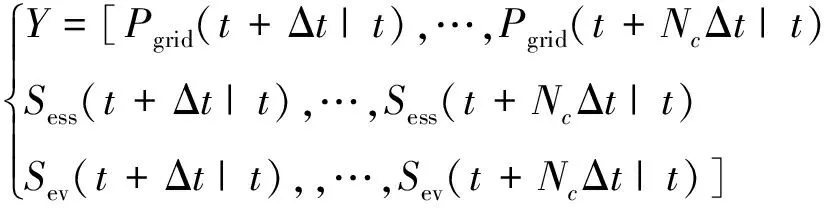
(33)

(34)

3.2.3反馈校正

随后，基于滚动优化模型求解得到当前t时刻对应控制时域内的最优控制序列，执行其中第一个控制动作，并对系统实时状态进行反馈修正，形成闭环最优调度方案，并在t+1时刻，基于新的短期预测信息，重复上述过程，以此形成智慧楼宇的日内滚动优化调度。

4 算例分析

4.1 算例设置

本文采取两类典型智慧楼宇进行对比分析，其中，居民、商业智慧楼宇的风机、光伏出力以及基础负荷日前预测值分别如图4(a)、(b)所示。同时，该地一日电价数据如表1所示，且购/售电价格系数为ρbuy=1、ρsell=0.3。每栋智慧楼宇中包含25家用户以及25辆EV，楼宇内每家用户的可转移负荷、可削减负荷的历史运行数据如表2、3所示。储能额定容量为400 kW·h，额定功率为50 kW，初始SOC为0.4，SOC的正常范围为0.2～0.9，自放电损耗常数εess=0.002 kW[18]。EV电池的额定容量为70 kW·h，额定功率为7 kW，到达充电站时刻SOC服从N(0.6,0.12)，SOC正常范围为0.2～0.9，自放电损耗常数εev=0.002 kW[18]。

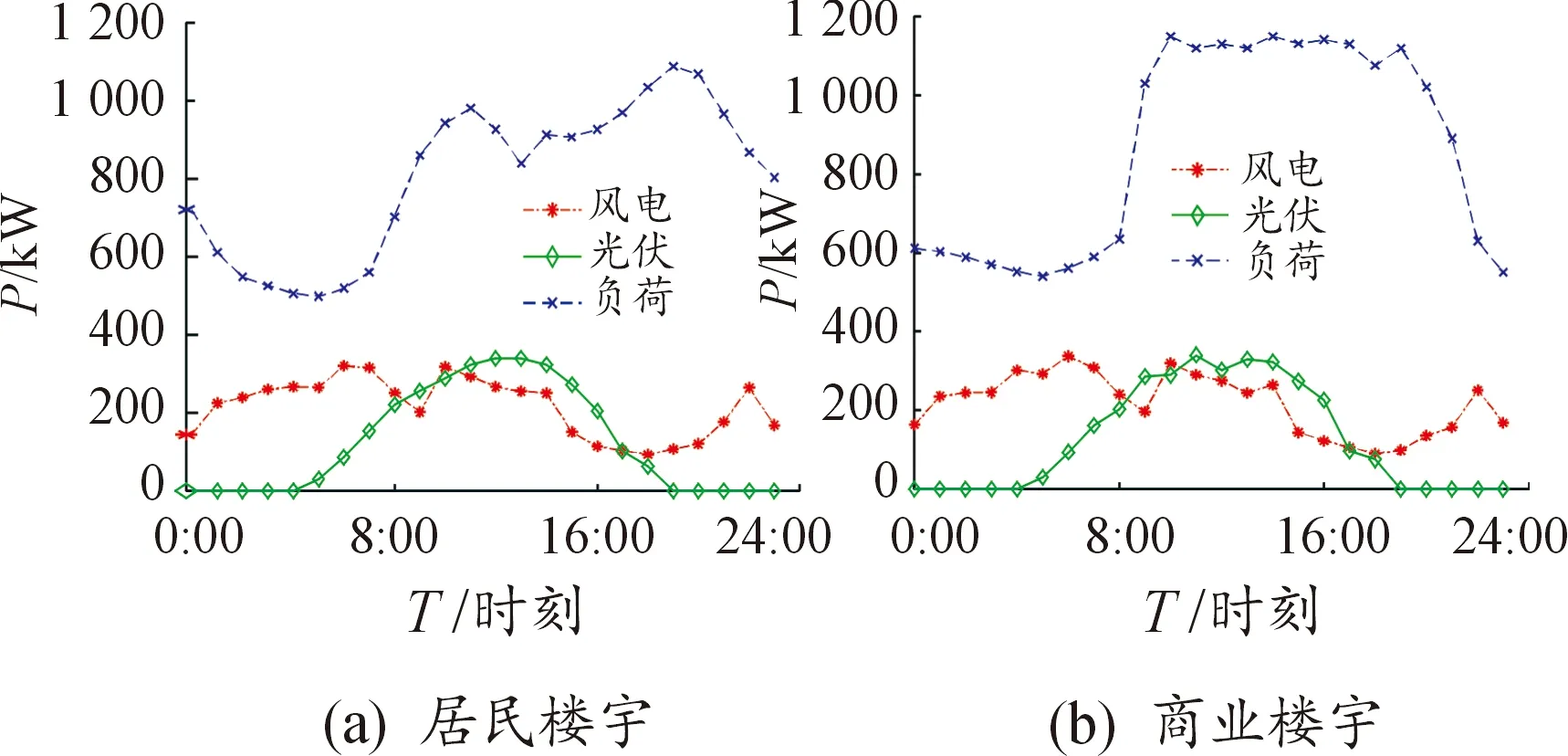
图4 风、光、负荷日前预测值曲线

表1 一日实时电价

表2 单个用户的可转移负荷运行数据

表3 单个用户的可削减负荷运行数据

4.2 日前优化调度结果分析

4.2.1日前优化调度方案

日前调度主要考虑系统经济性，并通过优化调整各设备的出力情况，实现系统一日运行成本最低。其中，居民楼宇与商业楼宇的日前优化结果分别如图5、6所示。

图5 居民楼宇日前优化结果

图6 商业楼宇日前优化结果

由图5、6可知，居民楼宇与商业楼宇的日前出力计划存在一定共通性，当处于高电价时段(19∶00—22∶00)，两者储能与DG均以最大功率向外放电，以减小购电成本，并满足负荷在高峰期需求；当处于低电价时段(0∶00—7∶00)，两者储能以最大功率充电，以满足次日用能需求；同时，在8∶00—9∶00期间，由于光伏开始出力且风电保持出力，而楼宇内负荷较低，此时两楼宇均向电网售电。然而，居民楼宇与商业楼宇对于EV充放电的调度结果存在明显区别，对于居民楼宇而言，EV在高电价时段(19∶00—22∶00)向外放电，并在低电价时段(0∶00—7∶00)充电，8∶00—11∶00间在网EV数量逐步减少，12∶00—17∶00几乎不参与V2G响应。对于商业楼宇而言，EV集中在13∶00—16∶00到达商业楼宇，且停留时长较短，因此主要集中在平电价时段(16∶00—17∶00)充电，并在高电价时段(18∶00—19∶00)放电，以减小电网负荷压力。

4.2.2日前需求响应分析

对于负荷侧，考虑用户可调度负荷的需求响应(demand response,DR)以及电动汽车的V2G响应，并通过调整可调度负荷的运行时间、功率以及EV充放电功率，优化负荷曲线。居民、商业楼宇需求响应结果如图7、8所示。

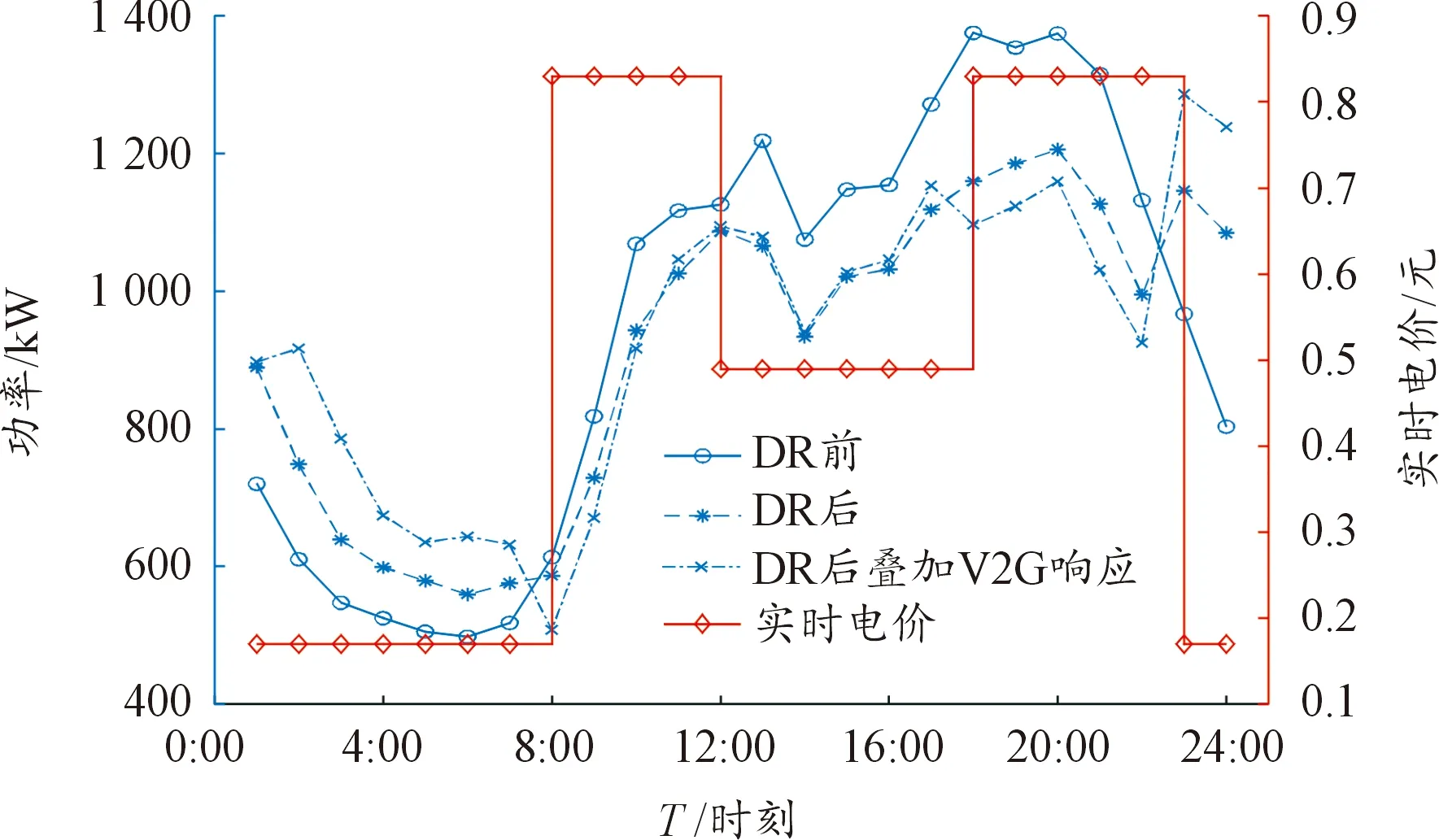
图7 居民楼宇日前需求响应结果曲线

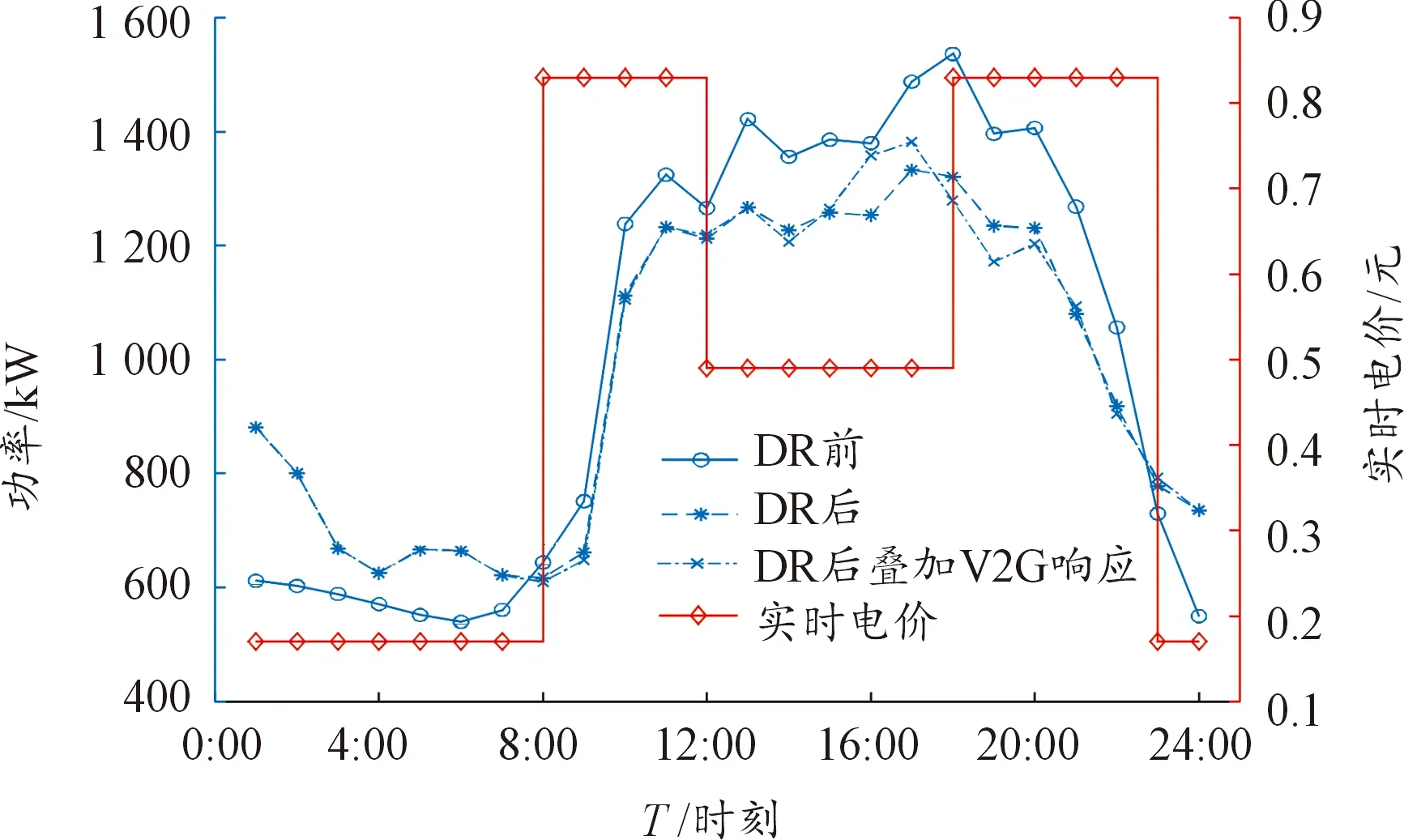
图8 商业楼宇日前需求响应结果曲线

由图7、8可知，在采取可调度负荷的需求响应后，居民楼宇与商业楼宇的负荷均呈现出明显的高峰期削减和低谷期加强的态势；而EV的V2G响应则呈现出明显的区域特性，当处于夜晚时段(20∶00—7∶00)时，EV集中停留在居民楼宇内，因此居民楼宇可以在高电价时段(18∶00—22∶00)对EV进行放电，在低电价时段(0∶00—7∶00)对EV进行充电，满足次日出行需求；当处于下午及傍晚时段(13∶00—20∶00)，EV集中停留在商业楼宇中，因此商业楼宇可以在平电价时段(12∶00—17∶00)对EV进行充电，在高电价时段(18∶00—20∶00)对EV进行放电，减小楼宇负荷压力。

为了进一步分析可调度负荷的需求响应与V2G响应对系统运行的影响，分析采取需求响应前后的系统状态变化，其结果如表4所示。同时，选取负荷峰谷差、负荷方差、总负荷以及系统运行成本4个指标进行分析。

表4 需求响应前后系统状态对比

由表4可知，在采取负荷的需求响应后，负荷峰谷差相比需求响应前得到明显降低(居民楼宇下降26.35%，商业楼宇下降28.12%)，负荷方差得到明显降低(居民楼宇下降48.26%，商业楼宇下降50.16%)，同时系统运行成本也得到降低(居民楼宇下降6.83%，商业楼宇下降6.81%)；在负荷的需求响应基础上继续采取V2G响应后，负荷峰谷差有小幅回升(居民楼宇回升16.94%，商业楼宇回升7.86%)，其主要原因在于23∶00与8∶00电价发生突变，而负荷并未突变，EV在此时集中充、放电，导致峰谷差有小幅回升(但峰谷差仍明显低于DR前负荷峰谷差)，同时系统运行成本得到了进一步降低(居民楼宇进一步降低3.26%，商业楼宇进一步降低2.04%)，系统经济性得到有效提升。

同时对比负荷的总体需求，可以发现，采取DR前后的负荷总体需求保持不变，表明负荷的需求响应虽然改变了负荷的运行时段及其在高峰期、低谷期的运行功率，但不会改变负荷在一天内的总体需求。因此，智慧楼宇的日前能量优化策略可以在满足负荷总体需求及EV充电需求的情况下，优化负荷在时间上的分布，提高系统经济性。

4.3 日内优化调度结果分析

在日内调度层，采取基于MPC的滚动优化调度方法，其滚动频率为每15 min 1次，预测时域与控制时域为4 h。同时，选取居民楼宇为例进行分析。

4.3.1风、光、负荷的日内短期预测

针对风、光、负荷的日内短期预测，本文利用日前预测功率叠加随机误差进行模拟[14]，如式(35)所示。同时，居民楼宇的可再生能源及负荷的日内短期预测结果如图9所示。

(35)

图9 日内短期预测值

4.3.2基于MPC的日内滚动优化效果

进一步地，为了体现本文所提控制方法在面对日内风、光、负荷出力波动时，对于联络线功率波动的抑制效果，对比采取MPC滚动优化和不优化下的联络线功率情况，其结果如图11所示。

图10 多时间尺度下的各单元优化结果

图11 联络线的功率控制效果

图11表明，不采取日内优化时，联络线功率会在日前计划值附近剧烈波动，系统将频繁地进行购/售电，这不仅会加大系统运行成本，也将降低系统运行稳定性。在采取MPC优化之后，联络线功率变得更加稳定，且与日前计划值基本一致。同时，MPC单次优化时间在0.08 s左右，满足在线应用需求，因此，上述仿真验证了所提控制方法的有效性。

4.3.3不同控制方法对比

为了进一步说明本文所提方法的优越性，将本文所提方法与传统单断面优化方法进行对比。其中，单断面优化方法是指基于系统实时状态，对系统控制量采取单步最优控制的开环优化方法。

由图12可知，当联络线功率的日前计划值出现大幅度波动时(如图12所示，3个时段分别在 6∶00 —8∶00，8∶30—10∶00，21∶30—23∶00)，在日内尺度上采取MPC优化与单断面优化后的联络线功率具有明显的优化差异。这是由于单断面优化作为一种基于系统实时状态的最优控制，其仅依赖系统的单步控制量对系统进行状态调整，面对较大的系统状态变化量，其单步控制能力有限，难以立即应对联络线的功率突变，而导致单断面优化出现了滞后响应的现象；而MPC优化则是基于系统未来一段时间内的状态预测信息做出的最优控制决策，可以提前对系统的控制量做出调整计划，以解决由于系统的单步控制量不足而难以及时调整系统状态的问题，进而减小日内尺度的联络线功率与日前计划值之间的跟踪偏差，很好地应对日内实际运行中可再生能源以及负荷的功率波动。

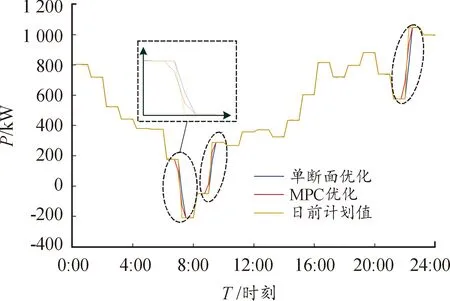
图12 不同控制方法的控制效果曲线

为了进一步比较2种控制方法下的联络线功率跟踪效果，利用均方误差(mean squared error,MSE)来刻画采取不同控制方法后的联络线功率值与日前计划值的贴近程度，其结果如表5所示。

表5 不同控制方法的控制效果对比

由表5可知，采用MPC优化后的联络线功率值与日前计划值的均方误差明显低于单断面优化策略，跟踪效果更好。

4.4 多时间尺度优化后系统性能评估

为了评估采用多时间尺度能量管理策略后的系统性能，本文从系统经济性及鲁棒性2个方面分析。针对系统经济性，考虑从日前计划到日内调整的全过程运行成本；针对系统鲁棒性，考虑日内联络线功率与日前计划值的偏差，定义其跟踪误差为采取优化策略后MSE与直接叠加扰动下MSE的比值，其表达式如式(36)所示。

(36)

式中:q为联络线功率跟踪误差；Popt(t)为采取不同优化策略后的联络线功率；P0(t)为联络线功率的日前参考值；Pdis(t)为直接叠加风、光、负荷日内波动下的功率值(不对设备出力进行日内调整)。

同时，为验证本文所提基于MPC的多时间尺度能量管理策略具有较好的经济性与鲁棒性，设计3组能量管理方案进行对比，分别为单断面优化策略(在日前优化的基础上，日内采取单断面优化)、DAP策略(仅采用日前优化，日内不调整设备出力)、Benchmark策略(日前阶段不采取负荷需求响应，负荷按照用户需求执行，并且日内不调整设备出力)。

由图13可知，针对日内风、光、负荷波动，MPC和单断面优化策略，可以通过调整各设备的日内出力情况，降低联络线功率波动，提高系统鲁棒性，而DAP与Benchmark策略则完全依赖于日内购/售电行为去平抑联络线功率波动，因此其联络线功率跟踪误差为100%，且其购/售电行为产生的成本以及与日前计划的偏差惩罚成本也会提高，降低了系统经济性。因此，MPC与单断面优化下的系统经济性与鲁棒性明显优于DAP与Benchmark。