考虑动态曲线特征的退役锂离子电池分选方法
2023-03-14聂金泉黄燕琴高洋洋李银银王聃轲
聂金泉,黄燕琴,高洋洋,李银银,王聃轲
(1.湖北文理学院 汽车与交通工程学院, 湖北 襄阳 441053;2.纯电动汽车动力系统设计与测试湖北省重点实验室, 湖北 襄阳 441053;3.襄阳市公共检验检测中心, 湖北 襄阳 441000)
0 引言
锂离子电池(lithium-ion battery,LIB)具有能量密度高、循环寿命长、无记忆效应等优点,已广泛应用于电动汽车和储能等领域[1]。自2021年,我国开始迎来第一批动力电池退役高峰期。退役电池如何处理成为新能源汽车产业迫在眉睫的发展难题。将其规模化应用于储能系统是解决该问题的有效途径[2-3]。考虑到电池组的最大可用容量主要由可用容量最小的电池决定[4],且越来越多的安全事故开始引起人们对于锂离子电池安全问题的思考[5]。因此,需要通过合理的分选方法延长电池的循环使用寿命,减少安全问题[6-7]。
国内外学者针对退役电池分选技术已经展开了大量研究[8-10],主要从提高分选效率和分选精度两大方向入手。Lai等[11]和郑岳久等[12]提出了采用电压快速预估容量的方法;Lai等[13]提出了基于融合算法进行容量内阻快速分选的方法。殷娟娟等[14]利用层次聚类分析和最小二乘原理建立了一套关于锂电池快速评价分选的流程,该方法最多只需要进行一次放电。张瑛[15]基于GA-BP神经网络算法训练健康状态估计模型,该方法在不同工况及不同电池种类的最大误差均小于2%,平均绝对误差及均方根误差小于1.5%。 骆凡等[16]提出了一种基于短时脉冲放电与电化学阻抗谱(EIS)相结合的退役电池快速分选方法,能有效降低能耗,有较大的实用价值。上述方法实现了对退役电池的快速分选,但一致性有待进一步提高。薛金花等[17]提出了基于老化机理分析的分选方法,分选出的电池组成的电池组在电池组容量利用率和温度一致性方面都具有较好的效果。杨超等[18]通过固定电压窗口的方法得到放电平台高度及长度数据,该方法能显著降低电池模组的不一致性。Liao等[19]通过容量测试、脉冲测试和电化学阻抗谱测试完成了一致性分选。王帅等[20]提出了多参数与动态电压分选相结合的方法,提高了退役电池模组的一致性。
为了提高退役电池的一致性,运用充电能量与放电能量之差表述一般测试过程中的化学极化和浓差极化等。通过多参数预分选,结合电压曲线和能量曲线动态分选的方法提高电池能量利用率,延长锂电池的循环使用寿命。同时,提出通过频率分布直方图和频率分布曲线分析确定K-means算法的K值,以解决K-means算法K值不确定的问题。
1 锂离子电池性能测试过程
1.1 测试设备
考虑温度对电池充放电过程中参数的影响,采用新威BTS 7.6.X电池综合测试系统,KCS-8900B可程式恒温恒湿试验箱,装载试验所需软件的上位机和单体锂离子电池搭建试验平台进行电池充放电测试。采用日置HIOKI BT3562内阻测试仪进行电池内阻和电压的测试。BTS 7.6.X电池综合测试系统拥有16通道。KCS-8900B可程式恒温恒湿试验箱温度波动度为±0.5 ℃。HIOKI BT3562内阻测试仪内阻测量精度为±0.5%,电压测量精度为±0.01%。实验平台实物见图1。

图1 实验平台实物
1.2 测试指标
1.2.1容量
文献[6]的研究表明电池组的容量比单体电池中的最小容量更低。电池组容量由所有单体电池中当前可放电最小电量和可充电最小电量的电池决定。
1.2.2内阻
电池的内阻直接影响电池外在参数差异。在循环充放电过程中,各单体内阻大小可反映单体间的一致性。所有单体内阻分布越集中,其一致性越好;反之,越分散则一致性越差。
1.2.3能量
考虑到充放电过程中,电池内阻和连接件内阻会消耗部分电能,Li+嵌脱的电化学极化和浓差极化也会导致部分能量损失,因此,可采用充电能量与放电能量之差表述电池的这种差异来描述一般测试过程中的化学极化和浓差极化等。
1.2.4电压
为了防止电池过充过放,最高的单体电池电压达到充电截止电压时整个电池组停止充电;放电时,当最低的单体电池电压达到放电截止电压时停止放电。
根据电池不一致性的表现形式,确定放电容量、充电电压、放电电压、能量差、充电内阻、放电内阻6个参数作为多参数的分选指标。其中,放电容量为电池在标准充放电条件下的充放电容量,用Q表示,单位为Ah;充放电电压为电池在标准充放电条件下充满和放完电时的电压值,分别用U1和U2表示,单位为V;能量差为电池在25 ℃标准充放电条件下充电能量与放电能量之差,用E表示,单位为Wh;充放电内阻为电池在标准充放电条件下充满和放完电时的内阻值,分别用R1和R2表示,单位为mΩ。
1.3 测试方法及数据
充放电流程参考GB/T31486—2015《电动汽车用动力蓄电池电性能要求及试验方法》、GB/T31467.2—2015《电动汽车用锂离子动力蓄电池包和系统第2分:高能量应用测试规程》,具体步骤:① 以2 A恒流放电至3 V;② 搁置1 h;③ 以2 A恒流恒压充电至4.2 V;④ 搁置1 h;⑤ 重复上述步骤1次,监测并记录电池的能量和容量等数据。
采用市购同批次的退役18650锰酸锂电池,使用时间为4 a。选取100节电池进行实验,电池参数如表1所示,电压、内阻、容量、能量等电池测试数据如表2所示。

表1 电池参数

表2 电池测试数据
2 电池分选
2.1 多参数分选
2.1.1分选变量的优化
考虑到各分选变量之间存在相关性,为了减少分选变量,简化计算,对退役电池的分选变量进行因子分析,式(1)为因子分析模型。
(1)
式中:f1,f2,…,fl(l≤m)为X各分量的公共因子,fi的均值为0,方差为1,相互独立;εi为xi的特定因子,只对xi起作用。εi均值为0,且各εi相互独立。f与ε独立,X均值为0,协方差阵∑=(σij)m×m,矩阵A=(aij)称为因子载荷矩阵。A中的元素aji称为xi的方差在fj上的载荷。
对于电池的多分选变量,可以利用KMO检验和Bartlett球度检验判断是否适合做因子分析[21]。KMO检验通过分选变量之间的相关系数来判断是否适合做因子分析,KMO值越大,则各分选变量间的相关系数越大,越适合做因子分析。Bartlett球度检验通过判断相关矩阵来检验分选变量是否适合做因子分析。Bartlett球度检验的原假设为相关矩阵是单位阵,只有拒绝该假设,因子分析才有意义,而要拒绝该假设就需要Bartlett球度统计量相应的概率值Sig小于给定的显著性水平。
1) 相关系数矩阵求解
记有p个原始电池样本,x1、x2、…xm为原始分选变量,z1、z2、…zl为新分选变量(主成分),此时m>l,由于分选参数量纲不同,故对原始数据进行标准化计算(均值为0,方差为1),然后根据式(2)(3)计算原分选变量间的相关系数矩阵。
(2)
(3)

2) 因子载荷矩阵求解
设λ1、λ2、…、λm为相关系数矩阵的特征值,η1、η2、…、ηm为相应的标准正交化特征向量,以特征值大于1为依据确定公因子数。求出公因子对应的标准正交化特征向量,则样本相关系数矩阵主成分分析的因子载荷矩阵为:

(4)
ηj为在迹的意义下fj对X的方差贡献:
(5)
gj为A的第j列各元素的平方和:
(6)
对因子载荷矩阵做正交旋转,使得到的矩阵C1=CD方差最大,其中D为正交矩阵。
3) 计算因子变量得分
采用回归法求各个原始数据在不同公因子上的详细数据值,即因子变量得分。以100节电池6个分选变量的数据作为输入,得到相关矩阵元素,如表3所示,6个变量有较大的相关性。

表3 分选变量的相关矩阵元素
根据KMO度量标准,检验值大于0.7时,适合做因子分析[21]。如表4所示,其检测值KMO=0.711>0.700,表明样本数据适合进行因子分析。此外,Bartlett球度统计量相应的概率值Sig=0.000<0.050,小于给定的显著性水平,拒绝原假设,可以进行因子分析[22]。通过KMO和Bartlett检验,表明各分选变量满足因子分析条件。

表4 Bartlett和KMO检验结果
采用主成份分析法进行因子分析,表5为主成份贡献率,其中F1、F2的特征值大于1,故选取F1、F2这2个公因子作为代表原分选变量的新变量。

表5 主成分贡献率
表6中每列数据表示公因子被原始变量表示的系数。
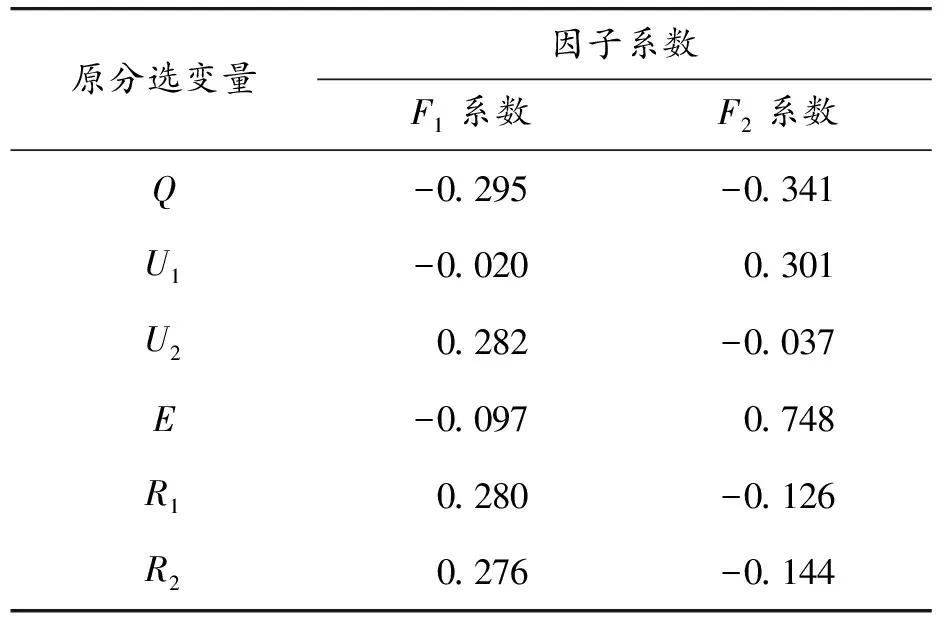
表6 成分得分系数矩阵
因子分析后6个参数转换成2个参数就可表达原来分选变量的大部分信息,所以选取这2个公因子作为新的分选变量。
F1=-0.295Q-0.020U1+0.282U2-
0.097E+0.280R1+0.276R2
F2=-0.341Q+0.301U1-0.037U2+
0.748E-0.126R1-0.144R2
2.1.2多参数分选结果
运用组间连接聚类方法,以平方欧式距离为度量标准对电池进行分类。

(7)
式中:xi和yi分别代表2个退役电池样本的某个变量,i和k代表变量个数。
分选结果如表7所示,采用式(8)(9)计算分选后各类电池电压的离散情况。

(8)

(9)
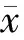
分选前100节退役锂离子电池的电压标准差为0.043 1,分选后第Ⅰ类电池的电压标准差为0.203 7,第Ⅱ类电池的电压标准差为0.011 1。可以看出,第Ⅰ类电池的电压一致性较差,表明电池组性能衰减是由极少数电池性能衰减引起的。

表7 多参数分选结果
2.2 动态分选
多参数分选只能体现电池的静态一致性,无法反映充放电过程中电池动态特性。动态特性分选法考虑了电池在充放电过程中的参数动态变化,结合多参数分选能够获得更高的一致性。多参数分选结果显示第Ⅰ类电池一致性相对较差,因此在第Ⅱ类(96节)电池的基础上再进行动态分选。
现有的动态分选方法普遍使用电压曲线进行分选,但该方法不能反映电流、容量等性能参数。任意一节电池充放电曲线如图2。恒压充电时电压曲线不能表示电池能量和容量的变化趋势;搁置时的能量曲线不能表示电池电压变化情况。电池组合时需同时考虑电压和容量的一致性以避免能量浪费,故同时使用电压曲线和能量曲线对第Ⅱ类96节电池进行动态分选,其数据如图3、4所示。
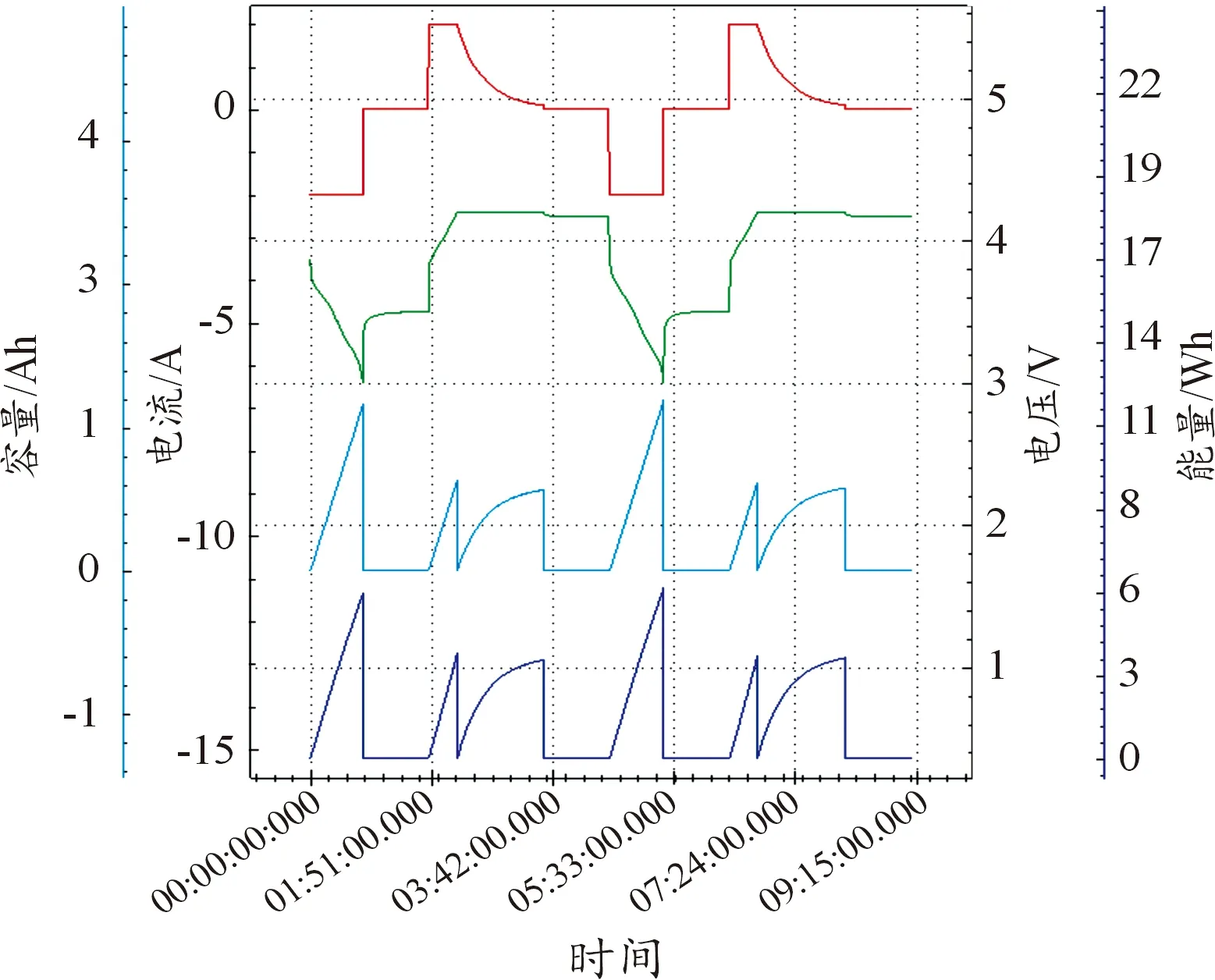
图2 电池充放电曲线
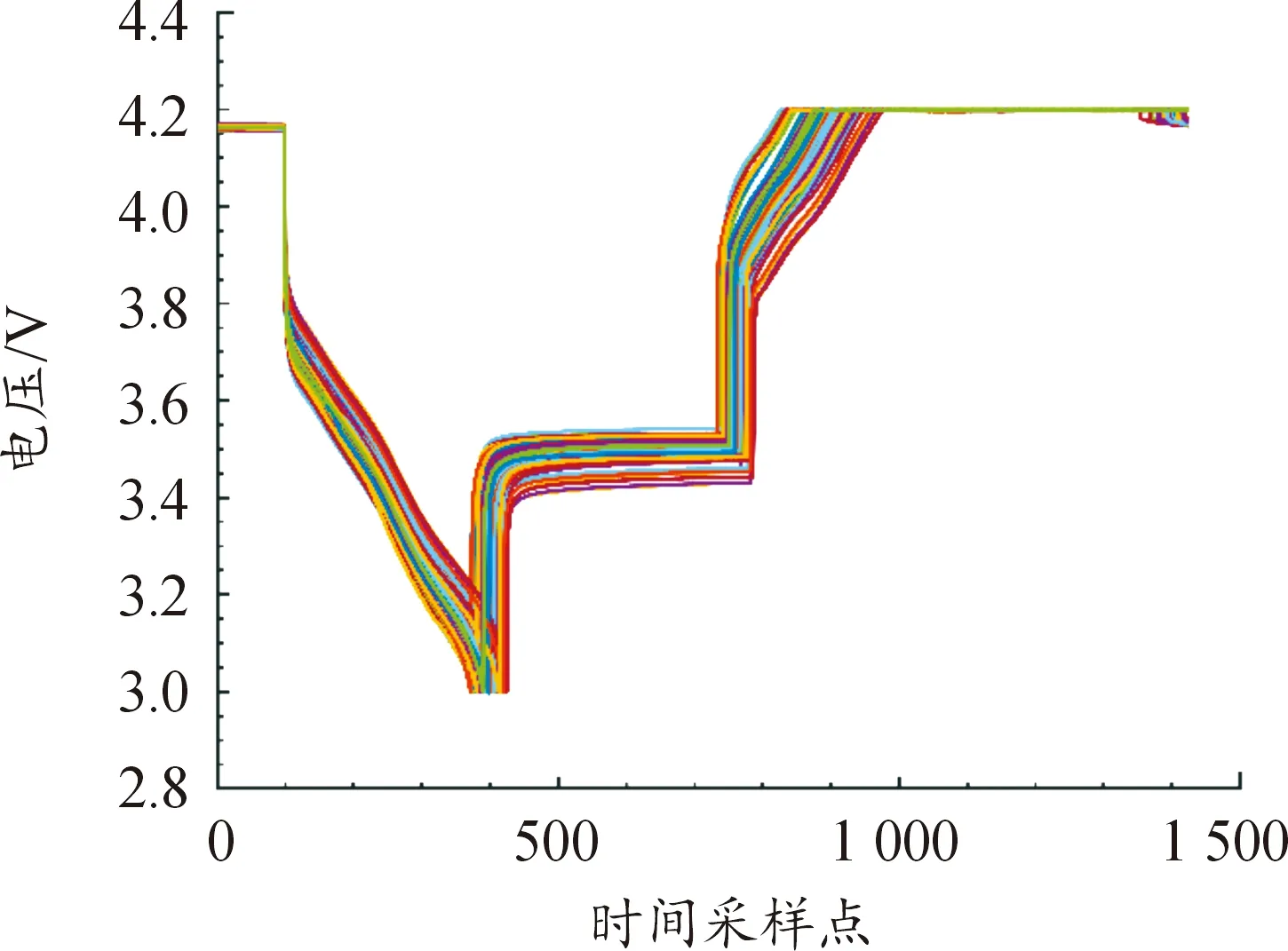
图3 电压曲线
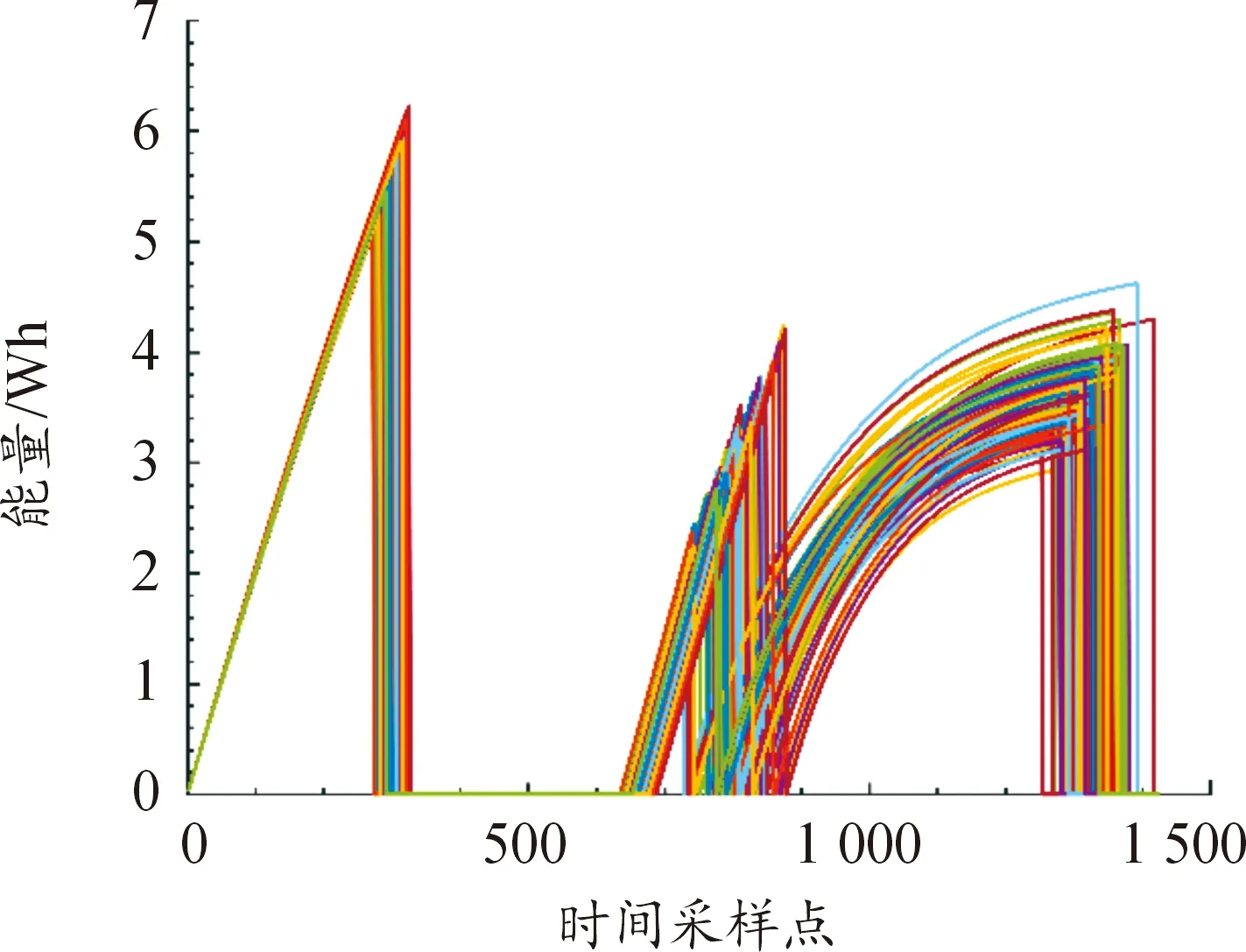
图4 能量曲线
算法设计:
步骤1采集96个电池电压和能量曲线上的数据并根据式(10)(11)分别归一化至[0,1]区间:
(10)
(11)
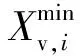
步骤2针对K-means算法存在K值不确定的问题,根据式(12)计算步骤1所得电压曲线和能量的距离均值,得到频率分布直方图和频率分布曲线,并根据直方图和分布曲线分析确定K值:
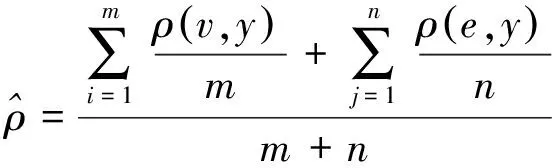
(12)
式中:m代表电压曲线上点的个数;n代表能量曲线上点的个数;ρ(v,y)代表电压曲线上点的纵坐标值;ρ(e,y)代表能量曲线上点的纵坐标值。
步骤3由步骤2确定K-means算法的K值,随机选取K个聚类中心曲线,并设置最大迭代次数;
步骤4根据式(13)计算剩余曲线到聚类中心曲线的平均距离,并将它们归类到距离3条聚类中心曲线平均距离最近的一类中;
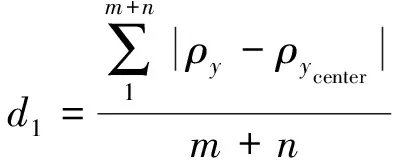
(13)
式中:ρy代表电压和能量曲线上点的纵坐标值;ρycenter代表聚类中心曲线上点的纵坐标值。
步骤5迭代步骤3—4并根据式(14)计算平均欧式偏差至所有曲线的平均欧式偏差最小,算法结束。
(14)
式中:p代表所有退役锂离子电池个数。
步骤6输出频率分布直方图和频率分布曲线、平均欧式偏差和聚类结果。
频率分布直方图与频率分布曲线如图5所示,数据近似围绕3个峰值紧密聚集,故可以设置3个聚类中心进行处理。经分析可知,第Ⅱ类96个电池可分为3类。
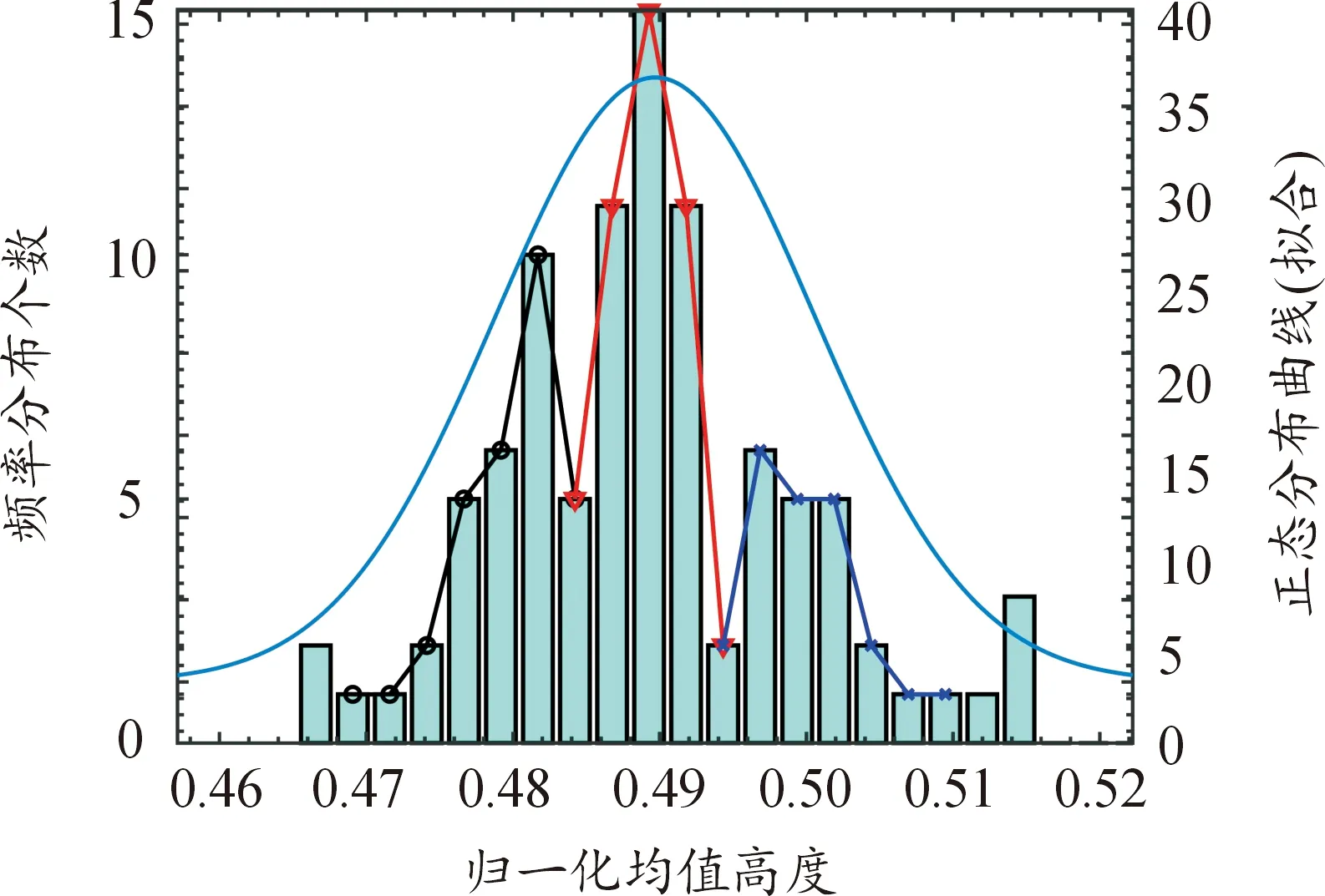
图5 频率分布直方图与频率分布曲线
图6显示了迭代100次后使得平均欧式偏差值最小时的3条聚类中心曲线。

图6 聚类中心曲线
平均欧式偏差可以反映迭代过程中所有曲线平均欧式偏差的变化。如图7所示,经过4次迭代后,平均欧式偏差趋于定值0.068 8,表明迭代后聚类趋于平稳,证明了算法聚类结果的优越性和稳定性。

图7 平均欧式偏差曲线
最终获得电池的分选结果如表8所示。
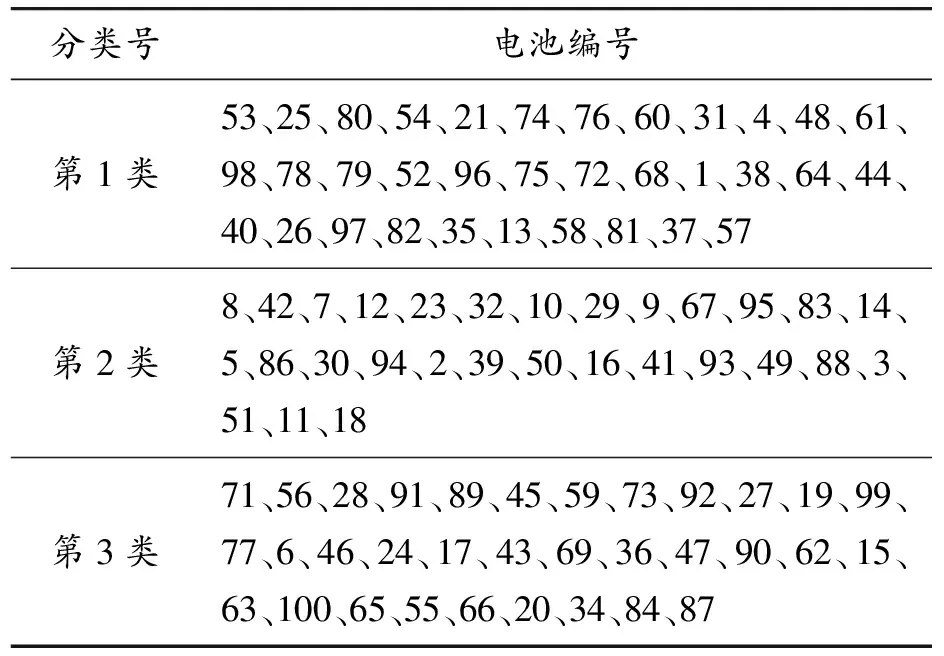
表8 电池最终分选结果
为了评价动态分选的效果,采用式(8)(9)计算各类电池充电电压、放电电压、容量的离散情况。
分选结果如表9所示。同时采用电压和能量曲线分选后(第1、2、3类)的电池充电电压一致性分别提高了约94%、82%、60%,放电电压一致性分别提高了约23%、41%、10%,容量一致性分别提高了约67%、54%、54%。

表9 分选结果
如图8所示,为了使分选结果更加直观,使用雷达图对分选结果进行分析。雷达图中离原点越近代表一致性越好。

图8 分选结果
3 结论
1) 第Ⅰ类电池的一致性较差,表明电池组性能衰减是由极少数电池性能衰减引起的。
2) 同时考虑电压和能量曲线分选后的退役锂离子电池充电电压一致性最大提高约94%,放电电压一致性最大提高约41%,容量一致性最大提高约67%。表明该分选策略得到的分选结果更好,对电池组性能提升有很大帮助。
3) 提出的通过频率分布直方图和频率分布曲线分析确定K-means算法K值的方法具有参考价值。
4) 分选前电池容量和电压存在较大的差异,从不同类别看,电压一致性和容量一致性并不是正相关,且不同应用场景对于各参数要求并不相同,表明同时考虑电压和能量曲线分选的必要性。接下来将对不同应用场景下电压和能量曲线的权重展开研究。
