基于模态参数的软基退洪闸有限元分析
2023-03-14刘建超
刘建超
(辽宁润中供水有限责任公司,辽宁 沈阳 110000)
在水闸运行期间,其性能评估和结构监测是十分关键的。结构监测和性能评估的有效手段就是建立有限元模型[1- 2],而参数的不确定性又会严重影响模型的建立,使模型不能真实准确地将动力学特性反映出来,会使水闸性能评估和损伤识别出现较大的误差。这几年,由于系统识别理论和监测手段的不断突破,以模态参数为基础的参数修正方法得到了快速发展,并引起了大量学者的关注,也给出了不同的修正方法[3- 5]。在之前研究人员提出的修正方法中,都存在一定的缺陷,比如个体算法很难达到全局收敛,而群体算法的效率低下等,仍需要深入研究和优化。
基于此,本文先提出了BAS-PSO优化算法,并和模态参数相结合,给出了一种新的方法来对模型参数进行修正。给出的BAS-PSO优化算法,不仅具备收敛精度高和收敛速度快的优点,同时解决了BAS算法中变量相互影响的问题。通过对实际工程模型的计算,发现本文的修正方法是科学合理的,有较大的可行性和良好的效果,能够给软基水闸有限元模型优化提供指导。
1 软基退洪闸概况
某软基退洪闸项目级别为Ⅱ级,800、200、100m3/s分别是其退洪流量、排涝流量和引水流量。此退洪闸结构具体包括消力池、闸室、进出水渠、上下游防护段、岸墙等。闸室结构为平底板整体式,7.0m为其闸底板顶高程,17.35m为挡洪水设计水位。退洪闸所在区域属于冲湖积平原,地处长江中下游,地势较为平坦。区内有较多的居民区、农田、水塘,其中水塘多处于临黄湖侧;农田多处于河堤外平坦区域;居民区多处于同马大堤里侧,属于软基闸。
2 修正退洪闸有限元模型参数
2.1 识别振动模态参数
为了更加准确地得到软基退洪闸振动响应信号里的振动模态参数,在识别振动模态参数时采用了IVMD-SSI法。第一步,以IVMD方法为基础,来进行退洪闸振动响应信号的降噪处理,从退洪闸振动信号里剥离出噪声信号,仅留存信号里的关键信息;接着,通过SSI法来识别经过处理后的信号,最后得出退洪闸振动模态参数。
2.2 GA-SVR代理模型
此次研究选取了密度和弹性模量这两个会对退洪闸结构模态参数产生较大影响的因素来作为待修正参数[6- 8],建立了一种数学模型表示软基退洪闸模态参数和待修正参数间的关系,即GA-SVR代理模型。此模型的基本原理是:借助拉丁超立方抽样法来得到样本较少的待修正参数样本集,在有限元模型里输入这些样本集来得出对应的模态参数集,参数通过非线性反映原理而被输入空间再映射到高维空间之中,通过超平面拟合和遗传算法对参数进行优化求解,以此构建出GA-SVR代理模型。
2.3 目标函数
目标函数的建立是根据两参数间相对偏差最低值来进行的,两参数分别是代理模型计算模态参数和退洪闸振动模态参数,目标函数如下所示:
(1)
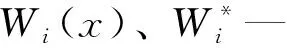
2.4 优化算法
Jiang等[8]给出的BAS算法是一种个体寻优算法,有着效率高、收敛速度比较快的优点,不过寻优求解的对象是多个目标函数时,因为个体局限性的影响,要将各个变量间的联系考虑在内是比较困难的。PSO算法是一种群体寻优算法,有着具全局收敛能力较好的优点,可以很好地解决BAS算法的缺点,不过寻常群体寻优算法在计算时效率不高,不能达到使用要求。所以,本文将两种算法进行结合,给出了一种新的优化算法,即BAS-PSO算法,此算法可以将个因素间的关系考虑在内,还有着较高的效率。它的基本原理是把粒子群里各个单体看成天牛单体,通过BAS算法来对单体适应度最优值进行确定,在根据PSO算法来对群体进行更新,以此来找出最优解[9- 10]。
3 小型模型分析
3.1 试验模型建立
以上述软基退洪闸为背景来建立模型,实际尺寸和模型尺寸比例为10∶1,如图1所示。退洪闸由钢筋混凝土制作而成,软基的填充材料选取了黏土、砾石和细,在软基周围布设了混凝土边墙进行约束。模型尺寸为:闸长、宽、高分别为1.43、1.37、1.62m,底板和闸墩厚都是为0.16m,0.32m为前工作桥宽,0.4m为后工作桥宽,软基长、宽、高分别是3.03、2.95、0.55m。此次研究中对模型进行了人工脉冲激励作用下的振动响应试验,在水闸左右对称安装了径向加速度传感器。将4个测点(B1-B4)从左到右安装闸墩右边的;并以测点B4为起点,从上往下安装了6个测点(B5-B10)。速度档为振动测试时选取的方式,1~100Hz为设置的测试频响范围,测试时选择不同的人工激励条件,进行了2次振动测试来对工况进行计算和验证。
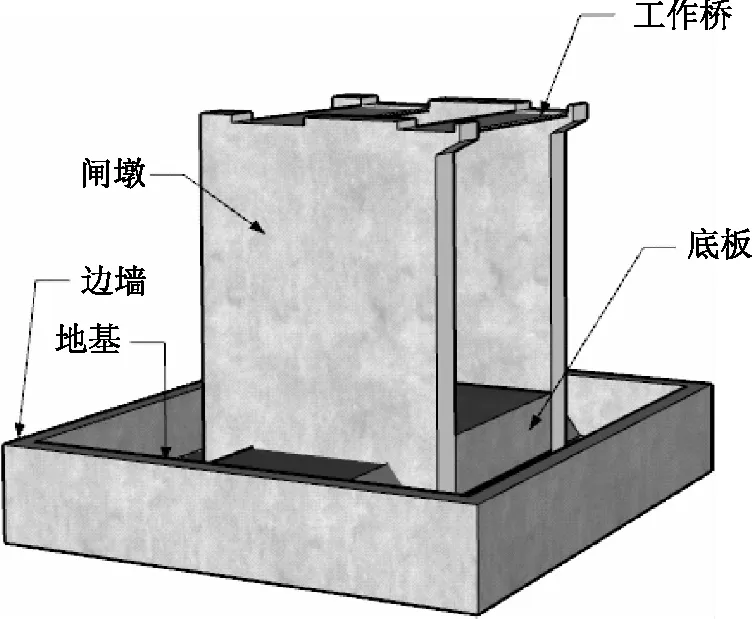
图1 软基退洪闸模型示意图
3.2 识别退洪闸振动模态参数
对比较典型的B7测点,选取IVMD法来分解其信号,通过互信息法能够得出4为模态数,图2为得到的信号分量(4个)时程线,表1是它的NMIC值,从表1中能够看出,所有信号分量的NMIC值都要比阈值0.02大,达到了分解标准。

表1 测点B7信号分量NMIC数值
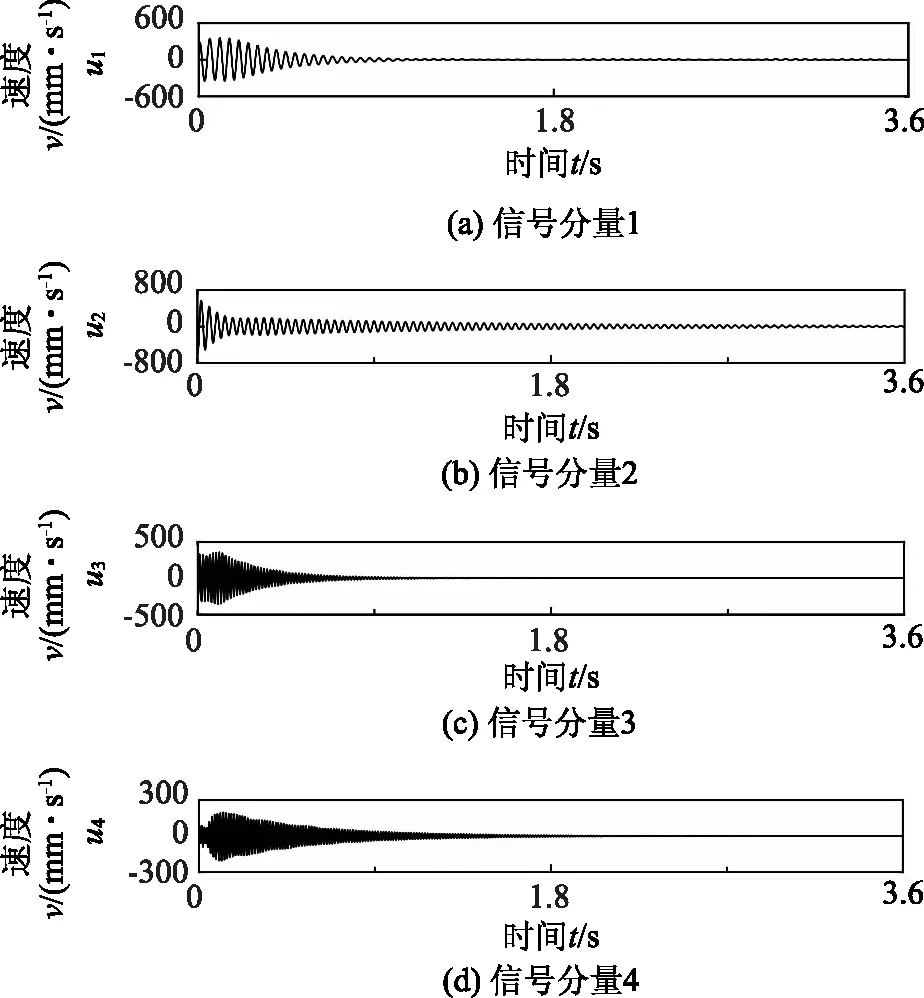
图2 B7测点信号分量(4个)时程线
在重构了典型测点信号分量后,可以绘制出测点B7降噪处理前后的功率谱密度曲线如图3所示、时程线如图4所示,从图3中能够看出,降噪处理可以很的将低频噪声从原始信号里除去。对降噪处理过的信号通过SSI法开展模态识别工作,可以得出振动模态参数。20.44、24.88、60.75、70.42Hz分别是退洪闸一、二、三、四阶的固有频率。第一、二阶振型分别是同向、反向振动,第三、四阶振型分别是同向、反向扭动,同时所有阶数的阻尼比都小于3.11%。

图3 B7测点降噪前和后功率谱密度曲线

图4 B7测点降噪前和后时程线
3.3 有限元模型建立
因为退洪闸混凝土养护和布置钢筋的方式有所不同,同时对于不同部位的地基,其压实度和所填充的材料也有所差异,这造成地基各部位的密度和弹性模量有所不同。所以,把退洪闸分隔成4个部位,分别是工作桥D、左(右)闸墩B(C)、底板A;把地基分隔成3个部位,分别是下层G、上层E和中层F。通过有限元软件来对退洪闸的有限元模型进行建立,如图5所示,借助法向约束来模拟地基底部和周围边墙的作用,通过搭接的方式连接闸墩和工作桥。
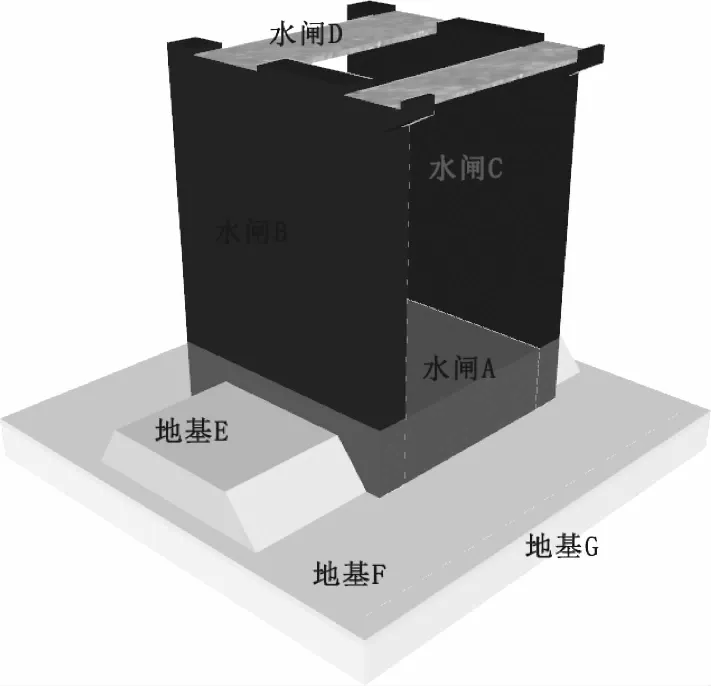
图5 软基退洪闸有限元模型
3.4 建立代理模型
检测了工作桥D的密度和弹性模量,分别是2511kg/m3和19.03GPa,同时以此为基准来对其余部位密度和弹性模量的范围进行确定;以此作为参考,并结合土力学标准来确定退洪闸其他区域弹性模量和密度的取值范围,结果见表2。在密度和弹性模量的取值区间里,用LHS法随机得出样本数据750组,同时用有限元模型对这些数据进行计算,可以得出同样组数的归一化振型系数和频率,将里面的50组数据当作测试集,其余数据组当作样本集。模型的初始参数设置为:200为初始种群大小,0.1和0.9分别为变异率和交叉率,26为最大代数,[0.1,100]为C的取值区间,[0.1,1000]为g的取值区间。通过GA算法来对模型里最优核函数参数g和正则化参数C进行搜索,之后就可以构建相关的GASVR代理模型。将典型测点和频率作为例子,加入三个指标来评价代理模型的精度,三指标分别是相关系数(R2)、平均绝对百分误差(MAPE)和方误差(MSE),表3—4为其评价结果。
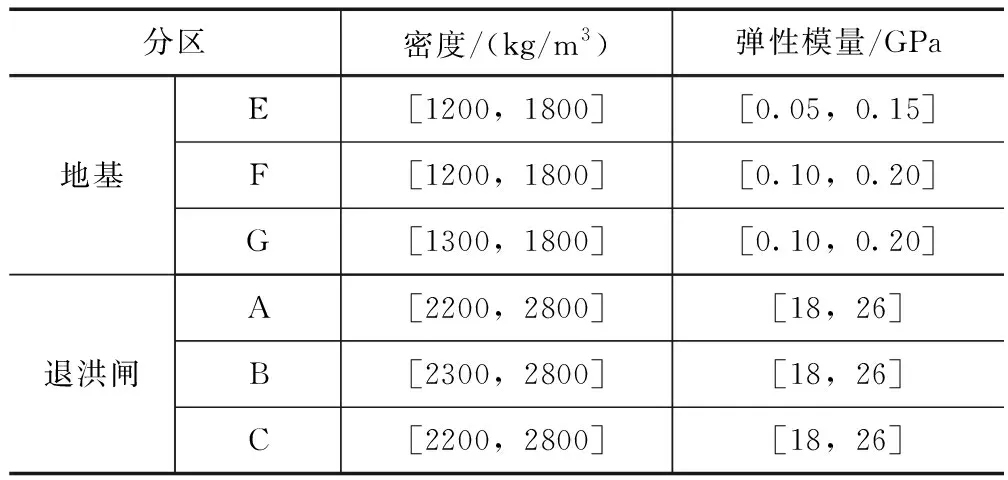
表2 各部位密度和弹性模量取值区间
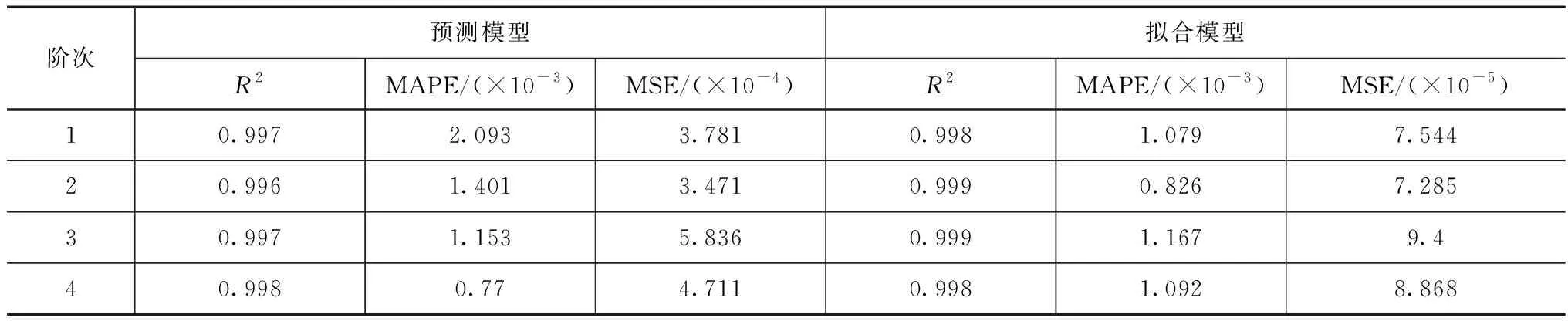
表3 频率评价指标
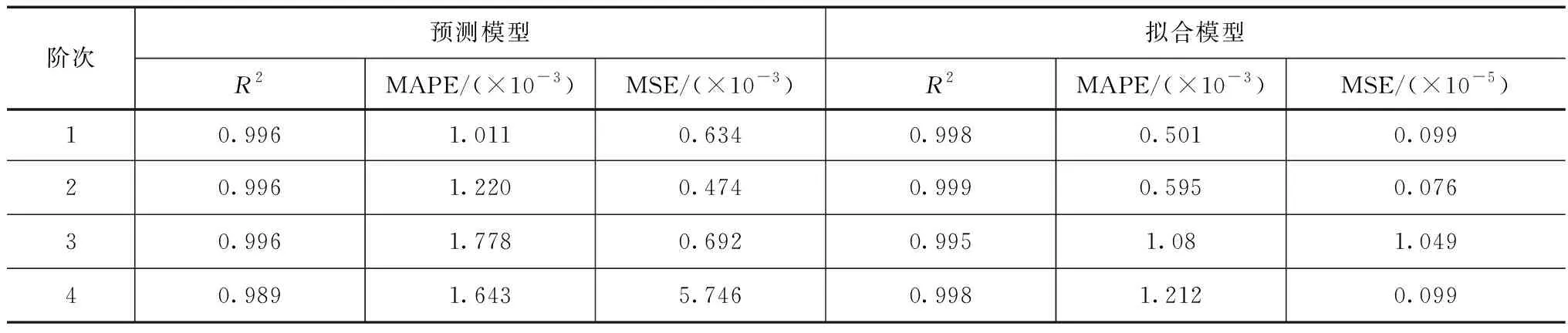
表4 振型系数评价指标
3.5 优化算法BAS-PSO
以式(1)为基础构建最优数学模型,通过BAS-PSO优化算法来对模型开展优化求解工作,能够得出密度和弹性模量在软基退洪闸各部位的值。并将此算法和BAS算法、AWPSO算法作比较,对比结果见图6。从图中能够看出,在12代时本文所用的优化算法就以收敛,而另外两种算法分别在14代(BAS算法)和16代(AEPSO算法)时收敛,同时BAS-PSO优化算法有着更低的计算适应度值,这表示此算法具备更好的精度、收敛效率更快的优点。
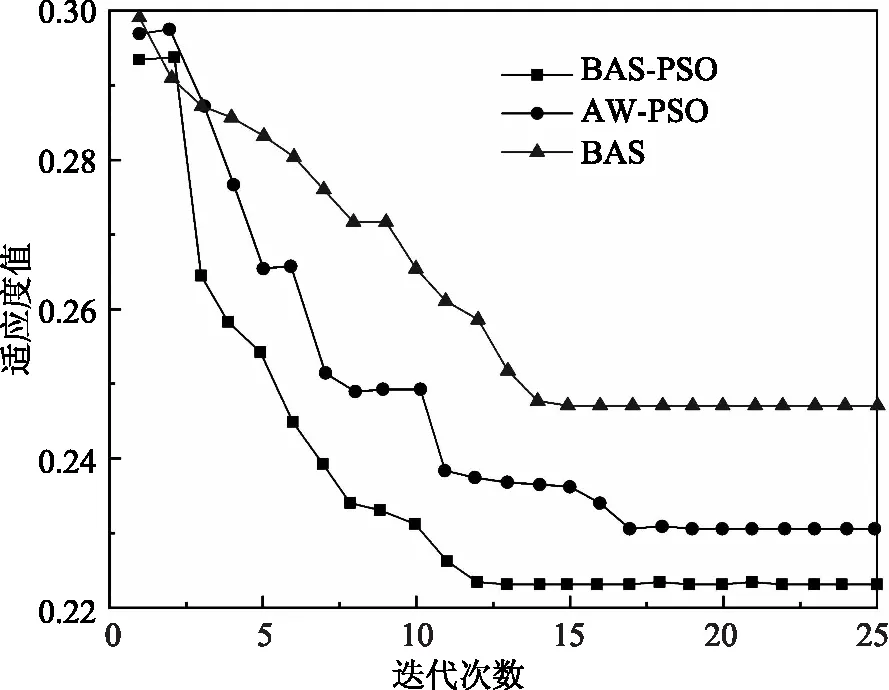
图6 3种算法对比结果
3.6 验证结果
为了对此方法是否准确进行验证,在有限元模型里输入修正后的密度和弹性模量,可以得出振型对比结果(如图7所示)和频率的对比结果(见表5)。对比结果反映出,-4.75%为频率的相对误差最大值,表示由参数修正后进行计算得到的频率和模态识别出的频率大致相同;12.72%振型系数计算值和识别值的相对误差大部分都小于12.72%,有较好的吻合度,不过B10、B20和B19测点的相对误差略大,分别是-16.94%、22.92%和-14.39%,这是因为闸墩底部位置处的测点振动幅值不大,噪声对这些测点的影响程度比较大,会造成振型识别出现一些误差。不过从整体来看,参数修正后计算得出的模态参数能够和与振动模态参数保持一致,说明此方法是科学合理的。
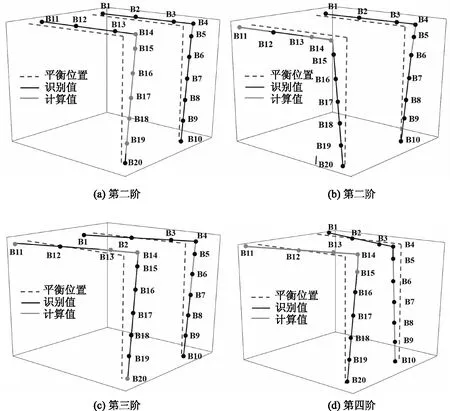
图7 综合压力指数在不同发展模式下的变化情况
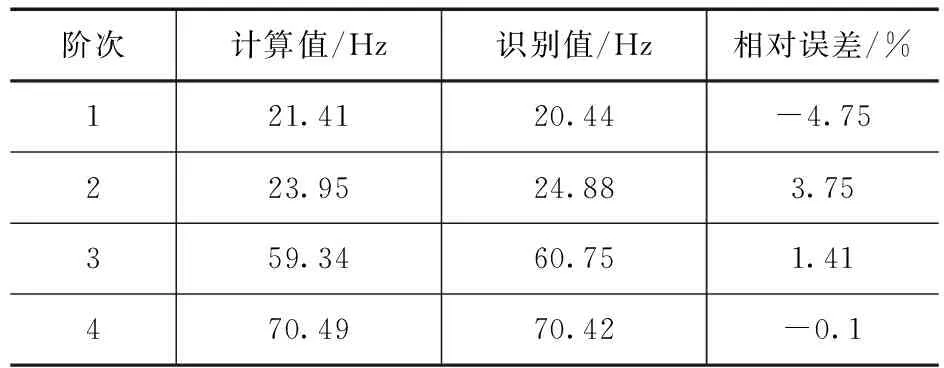
表5 频率识别值和计算值比对结果
4 结语
本文给出了一种新的修正软基水闸有限元模型参数方法,并以某软基退洪闸为例,进行建模计算,得出如下结论:
(1)给出一种新的软基水闸振动模态参数识别方法,即IVMD-SSI法,解决了VMD算法里的误差问题,能够很好的将噪声从信号里除去,增加模态参数识别的准确性。
(2)待修正参数选取了密度和弹性模量,构建了GA-SVR代理模型来表示模态参数和待修正系数之间的关系,可减少模型计算量,增加参数修正的准确度。
(3)制定了BAS-PSO优化算法,此算法收敛精度高、速度快,解决了BAS算法中变量相互影响的问题。通过对实际工程的计算表示,此方法有较大的可行性,可为软基水闸有限元模型优化提供指导。
