从结构化理解，探究数学概念教学——以“正切”为例

江苏省宜兴外国语学校

裴 姣

“获得的知识，如果没有完满的结构把它联在一起，那是一种多半会被遗忘的知识.”[1]布鲁纳的这句话告诉我们，知识要互相联系，架构成知识体系，才能更好地被我们理解和运用.在数学概念教学中，不仅要让学生经历完整的概念生成过程，也要重视知识之间的相互联系，挖掘知识点之间的相通之处，把知识串起来思考与认知.由点到面理解概念，更有助于学生抽象出数学概念，认识概念的本质，进而培养数学抽象思维，提升数学核心素养.下面，笔者以苏科版九年级下册第七章第1节“正切”(第1课时)的教学为例，谈谈基于结构化理解数学概念教学的实践与思考.

1 教学准备

1.1 教材分析

“正切”是在学生已有相似三角形相关知识的基础上，从感受台阶的倾斜程度这一实际生活问题中，提炼出角度与三角函数值之间一一对应的数学模型，建立了直角三角形中锐角和边的关系，是对勾股定理边和边关系的补充.本章内容分为锐角三角函数的概念、用锐角三角函数知识解直角三角形及其应用两个部分.正确理解“正切”的概念，既是学习“正弦、余弦”概念的基础，也是理解、利用直角三角形中边、角之间的关系解直角三角形，进而最终解决生活中测量、工程、物理等问题的关键.

1.2 教学目标

(1)从生活问题中探究正切的概念，认识直角三角形中锐角的正切.

(2)会求特殊角度的正切值.

(3)初步感悟模型思想、数形结合思想，培养抽象思维能力.

1.3 教学重点、难点

重点：掌握锐角的正切概念，会求锐角的正切值.

难点：理解角度与正切函数值之间的一一对应关系.

1.4 学情分析

学生已经学习了相似三角形的知识，具备运用相似的性质来解释只要锐角确定，这个锐角在不同直角三角形中对边与邻边的比值也是确定的.学生已经具备了借助图形找出直角三角形中边、角之间关系的能力.

2 教学过程

2.1 情境化感知概念

情境引入：图1中哪个台阶更陡？

图1

通过观察，学生能发现右图更陡，因为它的倾斜角度更大.

设计意图：从熟悉的生活情境入手，根据生活经验，学生能感知到，倾斜角度越大斜坡越陡.教师引导，除了角度外还能根据直角边来考虑倾斜程度，把实际问题数学化，抽象出直角三角形模型，从而把焦点转移到直角三角形中两条直角边的关系上.

2.2 探究中触及概念

探究一：图2-1，2-2，2-3中哪个台阶更陡？你是如何判断的？

图2-1 图2-2 图2-3

学生比较图2-1,2-2，发现水平距离都是8时，垂直高度大的台阶陡些；比较图2-2，2-3，当垂直高度都是6时，水平距离短的台阶陡些；从而可以得出图2-2中的台阶最陡.教师追问,图2-1，2-3中没有一条直角边相同该怎么比较呢？学生联想到可以构造有一边相同的相似三角形，且不改变台阶的倾斜角度.如图3，在图2-3中作出水平长度为8的相似三角形，运用相似比算出水平高度是4.8，得出图2-3中的台阶比第图2-1中的台阶略陡些.同样，把图2-1中的水平距离放大为10，运用相似比计算出水平高度是5，也能得到相同的结果.

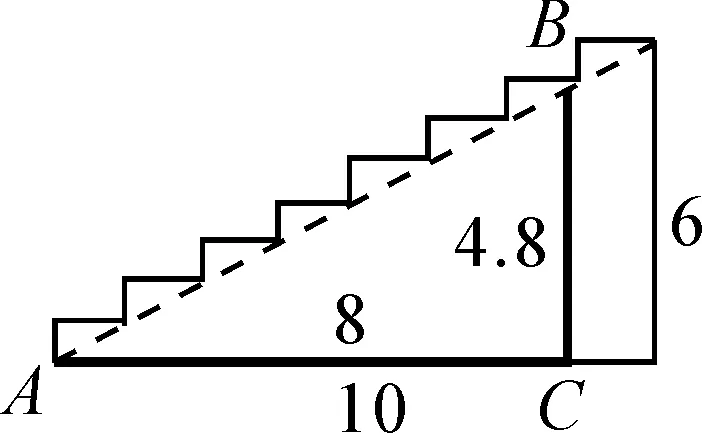
图3

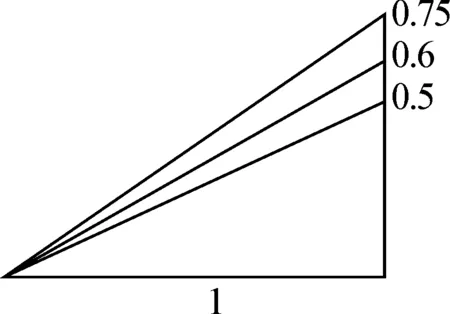
图4

追问：已知两条直角边，你有比较的方法吗？

通过上面的思考，学生知道需在一条直角边相等的情况下，再比较另一条直角边，相似是转化的知识支撑.引导学生把图2-1，2-2，2-3都转化为水平长度为1的直角三角形，运用相似比算出各自的垂直高度.当水平长度都是1时，图2-1，2-2，2-3中三个台阶的垂直高度分别为0.5,0.75,0.6，如图4.在同一幅图中，哪个台阶更陡，结果更为直观.进一步发现，计算出的垂直高度就是直角三角形两直角边的比值，通过比值的大小就能比较“陡”的程度高低.

设计意图：提供三个边长不同的直角三角形，意在让学生感受直角边长度能影响台阶“陡”的程度，在逐步探究中明晰思路，除了倾斜角外，两条直角边的比值也能确定台阶“陡”的程度.

探究二：比较图5的两个台阶，你有什么发现？

根据图中标识的数据，学生能判定两个三角形相似，推导出两个台阶的倾斜角相等.

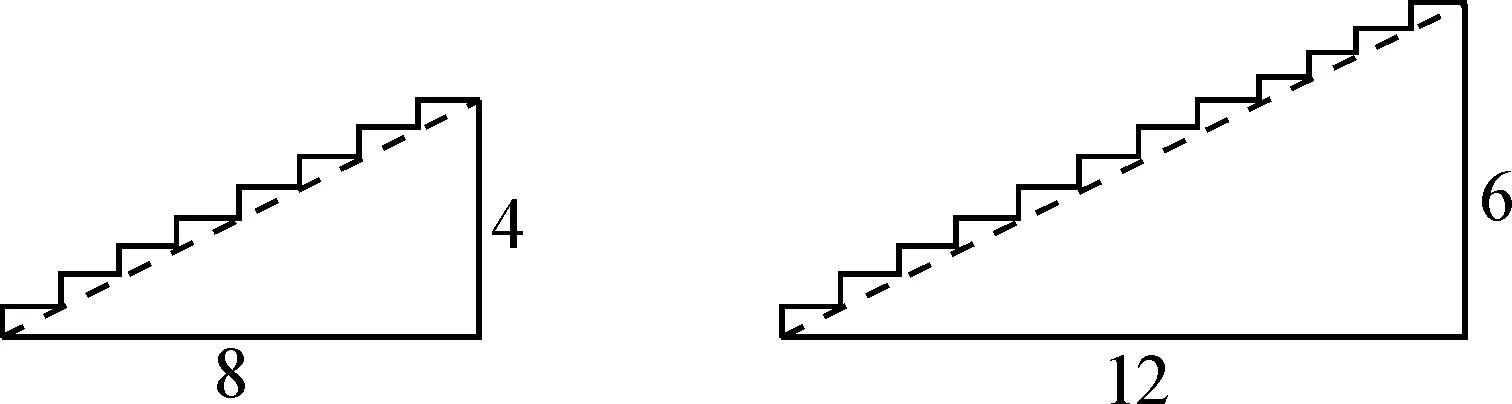
图5

设计意图：探究二提供的相似三角形是两个直角三角形关系的特殊化，在从一般到特殊的过程中，学生锁定的思考路径是利用直角三角形两条直角边的比值来确定台阶陡的程度，为下文给出正切的概念做好了充分的铺垫，让学生在丰富的素材中增强感受和体验.通过探究让学生经历概念形成的全过程，增强学生的体验，符合学生的认知规律和抽象思维特点.

2.3 提炼中表征概念

探究三：如果锐角A的大小确定，我们可以做出无数个以锐角A为内角的直角三角形.

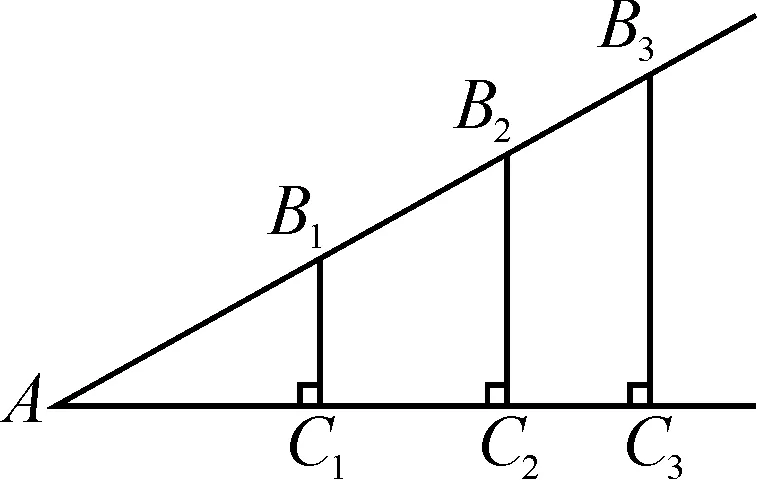
图6

(2)改变∠A的大小，(1)中的等式成立吗？

(3)(1)中等式的比值随着∠A的变化而变化吗？

根据相似三角形对应边成比例，(1)中的等式成立；当∠A变化时，(2)中等式仍然成立；(3)中等式的比值随着∠A的变化而变化.归纳：如果直角三角形的一个锐角的大小确定，那么这个锐角的对边与邻边的比值也确定.

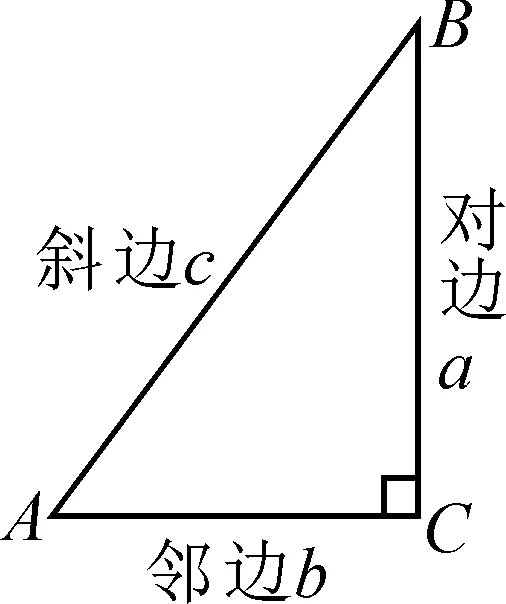
图7

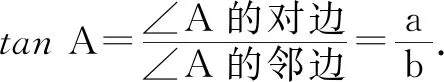
设计意图：学生在原有知识基础上，经过观察与分析，操作与思考，感悟出相似直角三角形的边与边的比值随着锐角的变化而改变，当锐角的大小确定时，比值也确定.初步建立起函数的一一对应关系，渗透模型思想，这样利用直角三角形来定义“正切”就水到渠成.

2.4 运用中深化概念

例1如图8，在Rt△ABC中，∠C=90°，AC=4，AB=5，求tanA.

分析：首先运用勾股定理求出直角边BC，再根据正切概念求锐角A的正切值.

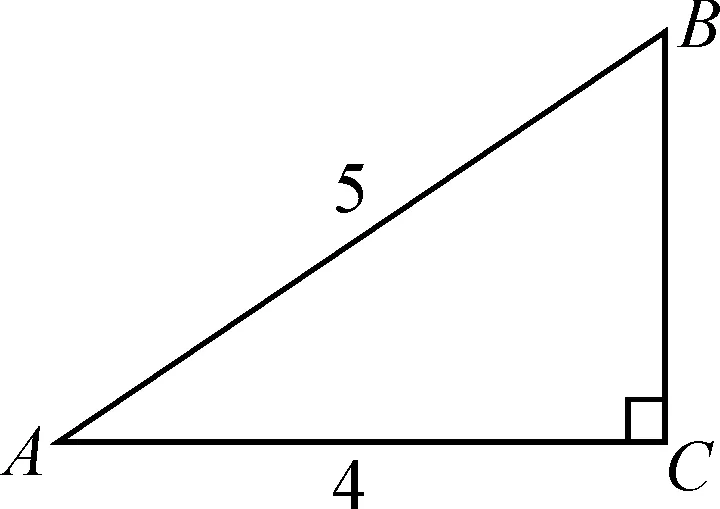
图8

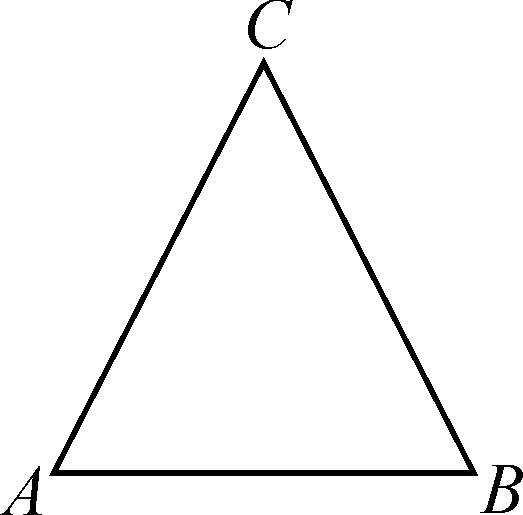
图9

例2如图9,已知等边三角形ABC，求tanA.

分析：添加辅助线构造直角三角形，运用等边三角形“三线合一”、勾股定理求出锐角A的对边与邻边之比.

设计意图：正切概念起源于直角三角形，运用正切函数解决问题就要放到直角三角形这一几何背景中.从例1到例2体现了从现成的直角三角形发展为构造直角三角形，让学生明确运用概念的条件.在例题求解中，学生认识到正切值是一个比值，没有单位，tanA是一个整体，不能拆开，通过初步运用概念，深化对概念的理解.

2.5 结构化理解概念

正切函数是锐角三角函数的一种，理解正切概念需有相似三角形的知识储备，正切函数在测量等实际问题中运用广泛.正切概念生成过程如图10所示.

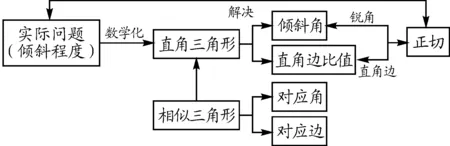
图10

3 教学思考

3.1 丰富学生体验，促进概念生成

数学概念课，若把只介绍概念、讲清楚例题、让学生会用作为课堂达成度的标准，那么，这样的概念教学课只完成了知识点的教学，学生只能学到知识点和解题方法，但思维和能力并没有得到提升.数学概念教学要引导学生从身边熟悉的素材入手，用数学的眼光去观察、思考问题，用数学语言表征概念和自我建构，这样概念的产生才会顺理成章，学生也能欣然接受.

3.2 渗透数学思想，深化概念认知

本课中，正切概念生成后，还需要表达和运用概念，达成对概念的深层认知.在运用正切表达和解决实际问题的过程中，教师要引导学生不断感悟模型思想，锐角的正切值随着锐角的变化而变化，相等的锐角正切值相等，跟所在直角三角形的大小无关，从模型思想中进一步体会正切概念的本质.本课中，也处处蕴含数形结合思想，分析题意，画出图形，结合图形从直观处体会边和角之间的关系，理解概念的实质，体现数与形巧妙结合，更有助于概念的形成与运用.

3.3 结构化理解概念，培养学生抽象素养

数学具有整体性，数学知识前后贯通，上下关联.概念教学要充分挖掘知识的生长点和延伸点，寻求新旧知识的关联，实现新旧知识的转化，构建成知识体系.让学生对概念的理解从表象化发展为本质化，从形式化发展为结构化，在建构知识体系的同时，培养理性思考的习惯与创新意识，发展数学抽象素养.