生长中发现 发现中生长
——以折叠问题为例
2023-03-14内蒙古包头市昆都仑区教育教学研究中心
内蒙古包头市昆都仑区教育教学研究中心
吴宝岩
传统“教学中对问题的解决只是展现解法、展现思路,但对思路的寻找过程以及为什么要这样解决、怎样想到这样方法的动态思维重视不够,对解决问题中思维与策略的自然性与合理性揭示不够.”[1]下面笔者以折叠问题为例,谈谈运用生长数学教学理念,让学生在解决问题中生成动态思维的一些思考.
1 “找准生长点”和“选好生长路径”
1.1 常见“点对点式”问题呈现

图1
原题1(2014安顺)如图1,矩形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E,AD=8,AB=4,则DE的长为.
这是一道典型的折叠问题,学生只要发现BE=DE(或由教师启发得到),运用勾股定理计算就可以得到答案.
解:设DE=x,则AE=8-x.
根据折叠的性质,得∠EBD=∠CBD.
因为AD∥BC,所以∠CBD=∠ADB.
因此∠EBD=∠EDB.于是BE=DE=x.
在Rt△ABE中,根据勾股定理,得
x2=(8-x)2+16.
解得x=5.
故DE=5.
通常在接下来的教学过程中就会进行类似问题的变式训练,以求通过刷题获得解题技能.
本题的解题关键在于发现“BE=DE”这一特殊关系,或者说这一类问题的解题模式是“先发现结论,后计算答案”,即“先定性分析、后定量分析”.“发现结论”进行定性分析就是学生动态思维生成的过程.既然“发现结论”比“计算答案”更重要,不妨把问题设置为开放式问题,让学生去“发现”,在“发现”中学会思考,在“发现”中摸索解决问题的方法,在“发现”中生长自己的数学.
1.2 “定性把握与定量刻画”[2]
改变问题情境,设置“生长点”,“选好生长路径”,以“发现”为课堂主旋律.重新设计教学如下:
原题1改编:如图1,矩形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)根据已知条件,你能发现哪些等量关系?(先定性把握)
(2)若AD=8,AB=4,则可以计算出哪些量?(后定量刻画)
先只出示并研究第(1)问:根据已知条件,你能发现哪些等量关系?

图2
学生在独立思考后,得到△ABE≌△C′DE,进而得到BE=DE(△EBD等腰三角形),AE=EC′(△AEC′等腰三角形),更有学生提出如果连接AC′,如图2,能得到AC′∥BD,∠AC′E=∠EBD,∠C′AE=∠EDB,△AC′E∽△DBE等结论.
在学生发现了诸多结论后,再给出第(2)问:若AD=8,AB=4,则可以计算出哪些量?
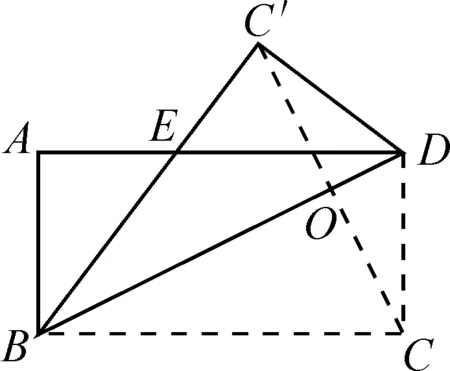
图3
“先定性分析、后定量分析”既是生长点,也生长路径.
2 解决折叠问题的几种策略
2.1 将原来的单一问题设计成开放性问题
学生在思考问题时,如果不受问题约束,思维会更发散、更开阔.学生连接AC′,CC′后,能发现、验证AC′∥BD, 并且能计算出AC′,CC′的长等“新结论”,足以说明问题,且在求解CC′长的过程中一题多解,方法灵活多样.学生对两个定点所连线段的位置与数量的确定性有了认知,使得以往“点对点式”思维变为“点对面式”发散思维,这对今后解题将带来巨大的影响.
2.2 设置阶梯,让无意注意向有意注意转化
针对原题1改编题的第(1)问,大部分学生都可以发现“新结论”,最容易被发现的是边和角的条件,其次是三角形以及三角形全等、相似等.教师引导学生根据获得条件的先后和难易梳理分析问题的思维链条:

学生在教师引导下,思考问题从无意注意向有意注意聚焦思维.
2.3 改变问题结构,探究新的结论
运用发现法引导学生“发现”解决问题的一般规律:先定性分析,后定量计算.这个顺序也是我们解题中经常用到的,即先根据题目的已知条件分析可能得到的潜在结论,然后在诸多“新结论”下重新组合条件来深入分析问题.在图3中,如果能够分析出两个三角形相似或者可用勾股定理时,就可以结合给定的数值进行计算.同样,我们针对原题2做相应改编.
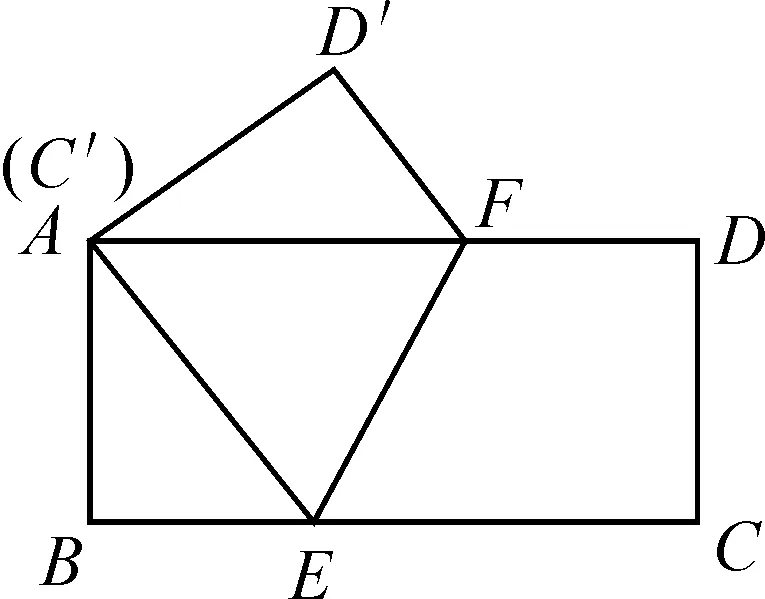
图4
原题2(2019大连)如图4,将矩形纸片ABCD折叠,使点C与点A重合,折痕为EF,若AB=4,BC=8.则D′F的长为.
原题2改编:如图4,将矩形纸片ABCD折叠,使点C与点A重合,折痕为EF.
(1)根据已知条件,你能发现哪些等量关系?(先定性分析)
(2)若AB=4,BC=8,则可以计算出哪些量?(后定量分析)
如图4,学生发现△AEF是等腰三角形.
如图5,若连接AC,交EF于点O,则△AFO和△CEO全等,且AC和EF互相平分.连结FC,如图6,于是有四边形AECF是平行四边形.

图5

图6

图7


图8
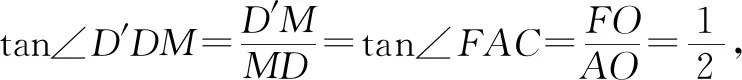
也有学生指出,求DD′的长可以借助△DD′F和△ACF相似来实现,△DD′F和△ACF都是等腰三角形且对顶角∠D′FD=∠AFC.但马上有学生指出,点C,F,D′三点不一定共线,即∠D′FD=∠AFC不能成立.有学生补充:△AD′F和△CDF全等,∠AFD′=∠CFD,而点A,F,D三点共线,可知点C,F,D′三点共线,所以∠D′FD=∠AFC.
“一石激起千层浪”, 对于学生连接AC和DD′,通过证明AC∥DD′来计算DD′长的过程中出现的关于三点是否共线的问题,虽是小意外,但却引发学生更深层次的思考.原题2改编题的教学设计初衷本来是模仿原题1的改编题训练思维,不曾想学生的思维一旦被激活,就像飞出牢笼的鸟儿,在数学的天空中自由翱翔!
2.4 课堂教学的终极目标是发展学生思维
对于学生连接AC和DD′,通过证明AC∥DD′来计算出DD′的长这个新发现,教师及时引导设问:你是怎么发现AC∥DD′?学生结合原题1改编题第(2)问中连接AC′后发现AC′∥BD,从而在图8中猜想AC和DD′是否会平行并设法证明.对于DD′长度的计算,虽然与计算AC′长度的方法不同,但由于点D和点D′的位置确定,所以坚信必定有办法能计算出来.
至此,开放性问题的设置充分释放了学生的思维,发散、发现的触角无所不往.发现法教学的模式让学生打开数学的大门,在数学的天地里自由驰骋,不断发现新的结论,再加之教师追问“怎么得到的”“怎么想到的”更是让学生进入大彻大悟的境界.
布鲁纳认为,学习知识的最佳方式是发现学习.这就要求在教学过程中实现由教师的“教”转变为学生的“学”,由“寻求单一答案”转变为“发现可能的结论”.这样一来,就将传统教学中解决单一答案的“点式”问题变为解决“面式”的开放性问题,学生在教师的引导下独立分析探究、发现结论、掌握原理和规律.
由此,创设情境,给学生探究的时间和空间,思维的空气、水和土壤,就能发现数学、生长数学.数学课堂经过这样的设计,才能真正发展学生核心素养.
