不同护栏透风率下桥面雪飘移的数值模拟
2023-03-14张天歌周晅毅
张天歌,周晅毅,顾 明
(同济大学土木工程防灾国家重点实验室,上海 200092)
在我国北部的多雪地区,桥面积雪会导致车辆难以通行,致使道路受阻;由风引起的桥面不均匀分布雪荷载可能会加剧该交通问题。为减小桥面风致积雪对交通的不利影响,需要对桥面雪飘移的机理进行探究,合理地预测桥面积雪的重分布形式,进而采取相应的措施。由于桥梁附近的流场受护栏的影响较大,在探究桥面雪飘移时需要考虑护栏的影响。
雪飘移问题的研究方法主要有现场实测[1]、风洞试验[2]和数值模拟[3]。近年来,随着计算机技术的发展,基于计算流体动力学(CFD)的数值模拟方法逐渐兴起,成为工程领域中研究雪飘移问题的有效手段[4],并广泛用于地面或建筑屋面雪飘移的模拟[5-8]。TOM INAGA 等[7]对建筑周边雪飘移的CFD模型进行了概述,并提出了一个模拟雪飘移的新模型。ZHOU 等对平屋面[8]、双坡屋面[9]上的雪飘移进行了模拟,预测了屋面上的风致积雪重分布。ZHU 等[10]对雪飘移的准定常模拟方法进行了改进,并将其用于高低屋面雪飘移的研究。周晅毅等[11]采用拉格朗日方法,对立方体周边的雪飘移进行了模拟,并考虑了颗粒运动后的质量浓度对雪层表面摩擦速度的修正。MA 等[12]结合现场实测和数值模拟,对路堤周围风致积雪堆积进行了预测。
然而,当前针对桥面雪飘移问题的研究依然较少。DUAN 等[13]采用数值模拟方法对桥面风致积雪重分布进行了预测,但其主要关注桥面的动力特性,没有对不同护栏下桥面雪飘移的特点进行探讨。
本文基于CFD方法,探究不同护栏透风率下桥面雪飘移的特点。首先通过一个平屋面案例,对本文数值模拟方法的正确性进行了验证。随后采用该方法进行桥面雪飘移的数值模拟。桥面上共设置4 道防撞栏,在模拟的过程中改变护栏的透风率(0%~100%),对比不同护栏透风率下桥面附近流场形式、摩擦速度、桥面雪浓度和桥面风致积雪重分布的异同,基于模拟结果对实际工程中桥梁护栏的设计给出建议。
1 数值模拟方法
1.1 数值模拟方案
风致积雪运动属于两相流运动,本文采用定常的欧拉-欧拉方法进行模拟。空气相采用Reynolds时间平均方法,湍流模型采用realizablek-ε 模型;雪相采用欧拉方法,通过附加一个雪相输运方程来模拟。模拟时假设空气相和雪相之间为单向耦合的,即雪在风的作用下发生飘移,而雪的飘移对风场不产生影响[14]。
1.2 雪相控制方程
根据雪颗粒运动高度的不同,可以将雪的运动形式划分为:蠕移(小于0.01 m)、跃移(0.01 m~0.1 m)和悬移(0.1 m~100m),在模拟时通常将蠕移包含在跃移中[15]。在悬移运动时,雪颗粒会因重力作用产生向下的沉降;而在跃移运动时,由于雪颗粒会在雪表面发生回弹,重力沉降的作用会被减弱。雪相的控制方程为[16]:
式中: φ为雪浓度;νt为湍流运动粘度;Sct为湍流施密特数;wf为沉降速度,在跃移层(wf,sal)和悬移层(wf,sus)取值不同。等式左侧分别为瞬态项和对流项,等式右侧分别为扩散项和考虑重力沉降的附加对流项。由于本文进行定常的数值模拟,因此不考虑雪随时间的瞬态变化(即瞬态项为0),只考虑雪的对流和扩散。
1.3 雪的侵蚀和沉积
雪表面的摩擦速度是衡量雪侵蚀和沉积的关键因素,其表示雪表面所受剪切力的大小,定义为:
式中:τ0为风作用下雪表面的剪切力;ρa为空气的密度。
雪的侵蚀和沉积通量可以采用NAAIM 等[17]提出的经验公式进行计算:
式中:Aero=0.0007为经验系数;u*t为阈值摩擦速度;下标ero表示侵蚀;acc表示沉积。可以看出,当雪表面的摩擦速度大于阈值摩擦速度时,雪表面会发生侵蚀,反之则产生沉积。
基于雪侵蚀和沉积通量的计算结果,可以得到单位时间积雪高度的变化量:
式中,ρb为雪的堆积密度。
2 数值模型
2.1 研究对象
本文采用一个典型的分体箱梁断面作为研究对象[18],桥面宽度(L)为49.0 m,断面高度(H)为4.0m,桥面初始积雪厚度为0.3m,桥面两侧和中部共设置4道防撞栏(以下简称“护栏”),护栏的高度为1.6m(高出雪面部分),根据护栏位置将桥面划分为5 个区域,如图1所示。护栏的透风率从100%(无护栏)到0%(不透风护栏)变化,变化间隔为12.5%,根据护栏透风率的大小可以将其分为:无护栏、高透风率护栏和低透风率护栏三种类型,见表1。

表1 工况描述Table1 Description of cases

图1 桥梁断面/cm Fig.1 Bridge section profile
2.2 数值模拟计算域和网格划分
由于桥梁轴向长度大,断面形状沿轴向基本保持不变,因此对桥梁断面建立二维模型。利用ANSYS/FLUENT软件对桥面附近的风场进行模拟;将雪相的输运方程作为额外的方程对软件进行二次开发,从而实现雪飘移的模拟。图2为桥面数值模拟的计算域。网格方案采用渐变的结构化网格,网格总数为7.0万,在桥面附近对网格进行了加密处理。图3为各种护栏透风率工况下桥面附近的网格,桥面首层网格的高度为0.05m,能够对跃移层和悬移层进行区分。经检验,在该网格方案下,计算结果具有较好的网格无关性。

图2 数值模拟计算域Fig.2 Computational domain of numerical simulation

图3 桥面附近网格Fig.3 Grid around bridge deck
2.3 数值模拟参数
在数值模拟的过程中,需要对模拟参数进行合理的选取[9]。我国北方天气干燥,雪颗粒易在风的作用下发生飘移,且在桥面上发生飘移的雪大多是新降雪,于是本文考虑干燥、新降雪的情况,雪的堆积密度取70 kg/m3[19-21],阈值摩擦速度取0.07 m/s[22-23]。湍流施密特数取1.0[15]。悬移层受重力沉降的影响较大,其沉降速度取0.5m/s[15],而跃移层受重力沉降的影响相对较小,其沉降速度取0.15 m/s。初始积雪深度取30 cm[24]。数值模拟的参数汇总见表2。

表2 雪飘移的数值模拟参数汇总Table2 Parameters in numerical simulation of snow drifting
2.4 边界条件设置
来流风速在桥梁高度方向上的变化不显著,因此在速度入口采用均匀的风剖面。根据气象资料,对我国北部某地区冬季风速数据进行广义极值分布(GEV)拟合,如图4所示,得到具有95%保证率的估计风速:8.5m/s。于是,在本文的数值模拟中,取入口处的风速为8.5m/s,入口处的湍动能k和湍流耗散率ε 用下式计算[25]:

图4 我国北部某地区冬季风速数据(1980-2014)Fig.4 W ind velocity during w inter in representative northern region of China (1980-2014)
式中:I为湍流强度,本文取0.12;Cμ=0.09为常数;μ为湍流动力粘度;μt/μ为湍流粘度比。
速度出口边界设置为自由出流边界,上下边界设置为对称边界,雪表面采用标准壁面函数。湍流模型采用realizablek-ε 模型,离散格式为二阶迎风格式。收敛标准为无量纲残差降至10-7以下,且收敛时桥面附近监测点的风速保持不变。
3 试验验证
3.1 验证对象
由于平屋面和桥梁断面在外形上具有一定的相似性,二者表面雪输运的条件也相似,因此选择平屋面作为本文的验证对象。以文献[26]中的平屋面为验证对象,该屋面原型高(HR)6.0m,长(LR)36.0m。
3.2 平屋面雪飘移风洞试验介绍
ZHOU 等[26]在同济大学1号风洞进行了平屋面积雪重分布的风洞试验。风洞试验的缩尺比为1∶25,缩尺后的试验模型长144 cm,高24 cm,如图5所示。该试验采用硅砂模拟雪颗粒,屋面模型上的初始硅砂厚度为4.0 cm,对应原型的初始积雪深度为1.0m。风洞试验的阻塞比满足小于5%的要求。限于篇幅,风洞试验的详细介绍见文献[26]。

图5 平屋面风洞试验模型/cm Fig.5 Flat roof model in w ind tunnel test
3.3 平屋面雪飘移数值模拟介绍
以文献[26]中的平屋面原型为模拟对象,进行平屋面雪飘移的数值模拟。数值模拟的计算域和网格划分见图6。为使该数值模拟条件与试验的条件一致,将初始积雪深度设置为1.0 m,其余数值模拟参数的设置与桥面雪飘移模拟中的一致。

图6 平屋面雪飘移数值模拟计算域和网格划分Fig.6 Computational domain and grid in numerical simulation of snow drifting around flat roof
3.4 验证结果
根据1.3节所述雪侵蚀沉积的计算方法,可以计算出平屋面上各个位置处积雪深度的变化,进而得到平屋面风致积雪的重分布。图7为风洞试验[26]和数值模拟积雪重分布的结果,其中,横坐标x/L表示屋面上点的相对位置,纵坐标为无量纲的积雪深度,为屋面初始积雪深度(1.0 m)。从图中可以看出,数值模拟结果和风洞试验结果总体吻合较好,仅在部分区域存在差异:在x/L= 0.3附近,数值模拟结果比风洞试验结果大8.6%;在x/L= 0.9附近,数值模拟结果比风洞试验结果小6.5%。
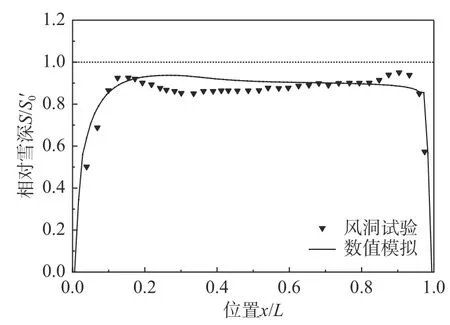
图7 平屋面积雪重分布Fig.7 Snow redistribution on flat roof
4 数值模拟结果
4.1 流场特性
图8为桥面各区域的流线图,仅给出护栏透风率为100%、50%和0%的三种工况,分别代表了无护栏、高透风率护栏和低透风率护栏的三种类型。总的来看,在各工况下,来流均在桥面的迎风前缘发生了分离,使桥面的迎风端产生了一个漩涡;在桥面的尾缘也产生了一个尾流涡。三种工况的差异主要体现在桥面中部(尤其是护栏附近)的区域。当护栏的透风率为100%和50%时,流场的形式大致相似;而当护栏的透风率为0%时,在护栏1的前端有另一个漩涡产生,此外,各护栏的背风侧也都产生了漩涡,其中区域2(即护栏1的背风侧)中的漩涡尺寸最大。

图8 桥面各区域流线Fig.8 Stream lines in each region on bridge deck
4.2 桥面(雪表面)摩擦速度
桥面摩擦速度是判断雪侵蚀和沉积的重要参数,其与桥面附近的流场密切相关。图9绘出了桥面摩擦速度的分布,相同类型的工况绘制在同一张图上。总的来看,当护栏的透风率大于50%时(图9(a)、图9(b)),桥面摩擦速度相对较大,基本均大于阈值摩擦速度(0.07 m/s);而当护栏的透风率小于50%时(图9(c)),桥面摩擦速度相对较小,在某些区域小于阈值摩擦速度。
在高透风率护栏情况下,桥面摩擦速度随护栏透风率的减小而减小,这体现了护栏对风的阻碍作用。而在低透风率护栏情况下,由于其流场形式复杂,摩擦速度随透风率的变化趋势也与高透风率护栏情况不同。以区域2为例,结合低透风率护栏情况下的流线图(图10)分析可知,当护栏透风率较小(但不为0%)时,护栏背风侧会因狭管效应形成一个气流加速区(图10),导致护栏背风侧的摩擦速度显著增大(图9(c))。此外,区域2的后部会出现一个漩涡,该漩涡的尺寸随护栏透风率的减小而增大(图10)。对比图9(c)可以看出,漩涡中部的摩擦速度较大,边缘的摩擦速度较小,且摩擦速度的极大值随漩涡尺寸的增大而增大。

图9 桥面摩擦速度Fig.9 Friction velocity on bridge deck

图10 桥面区域 2 流线图 (低透风率护栏情况)Fig.10 Streamlines in region No. 2 on bridge deck (cases with low barrier porosities)
为进一步分析桥面摩擦速度随护栏透风率的变化,将桥面摩擦速度分别按各区域和全桥面进行平均,得到平均摩擦速度,如图11所示。可以看出,桥面各区域平均摩擦速度都大于阈值摩擦速度(0.07m/s),这意味着桥面积雪在强风的作用下主要发生侵蚀。在高透风率护栏情况下,桥面大多数区域的平均摩擦速度随护栏透风率的减小而显著减小,仅区域1(迎风侧无护栏)的变化较为平缓。在低透风率护栏情况下,尽管护栏周围存在加速区和漩涡区,但其影响范围相对较小。从图9(c)和图11可以看出,低透风率时仅区域2的(平均)摩擦速度随护栏透风率的减小而增大,其他区域摩擦速度随透风率的变化不显著。

图11 平均摩擦速度Fig.11 Average friction velocity
4.3 桥面附近雪浓度
本文采用桥面首层网格雪浓度计算雪的沉积通量,首层网格的相对雪浓度见图12,纵坐标φ / φmax表示用最大雪浓度无量纲化后的相对雪浓度。可以看出,桥面雪浓度和桥面摩擦速度的分布规律相似。这是因为当桥面摩擦速度较高时,雪颗粒被风挟卷到计算域中,经对流和扩散后,该处雪浓度升高;而当桥面摩擦速度较低时,雪颗粒难以被风吹起,该处雪浓度也相应较低。

图12 桥面首层网格相对雪浓度Fig.12 Relative snow concentration at the first cell on bridge deck
4.4 桥面积雪重分布
图13为2 d 后桥面积雪重分布的计算结果,纵坐标S/S0表示无量纲积雪深度,其中,S0= 0.3m为桥面初始积雪深度。在高透风率护栏(大于50%)情况下(图13(a)、图13(b)),桥面各区域仅发生雪的侵蚀,基本不发生雪的沉积,且桥面积雪的侵蚀程度随护栏透风率的减小而减小,这体现了护栏对雪飘移的阻碍作用。同一工况下,区域1的侵蚀程度较小,而其他区域侵蚀程度相对较大,且各区域侵蚀的特征相似。在低透风率护栏(小于50%)情况下(图13(c)),受护栏背风侧加速区和漩涡区的影响,部分区域的积雪侵蚀程度随护栏透风率的减小而增大,这与桥面摩擦速度的规律是一致的。低透风率时较为显著的沉积主要发生在护栏1的背风侧(区域2 漩涡边缘),该处摩擦速度小于阈值摩擦速度,因此雪颗粒不能被风挟卷进入计算域,只能产生沉积。随着护栏透风率的减小,漩涡的尺寸增大(图10),沉积区域越来越靠近护栏(图13(c)),最大积雪沉积量约为初始积雪深度(30 cm)的1.25倍。

图13 桥面积雪重分布(2 d)Fig.13 Snow redistribution on bridge deck (2 days)
为了进一步分析桥面积雪随护栏透风率的变化趋势,将桥面积雪变化分别按各区域和全桥面进行了平均,得到平均积雪分布,如图14所示。可以看出,在高透风率护栏情况下,桥面积雪的平均改变量随护栏透风率的减小而减小;在低透风率护栏情况下,仅区域2的积雪平均改变量随护栏透风率的减小而增大,其他区域的变化不显著,这与平均摩擦速度(图11)的规律是一致的。

图14 平均积雪分布(2 d)Fig.14 Average snow redistribution (2 days)
在实际工程中,桥面上积雪的堆积会使道路受阻,为了减小风致积雪堆积对桥面交通的不利影响,建议在桥梁设计时采用高透风率(大于50%)的护栏。
5 结论
本文采用CFD方法,对桥面的风致积雪飘移进行了数值模拟,对比分析了不同护栏透风率下桥面风致积雪重分布形式,得出了以下几个结论:
(1)以平屋面为案例,对比了屋面积雪重分布的CFD模拟结果和风洞试验结果,两种结果吻合较好,表明采用CFD模拟得到的结构表面雪飘移结果可以满足工程精度的要求。
(2)护栏透风率对桥面积雪分布形式有显著的影响。当护栏透风率大于50%时,桥面上不会出现积雪的堆积,且桥面积雪侵蚀程度随护栏透风率的减小而减小;同一工况下,区域1的侵蚀程度较小,而其他区域的侵蚀程度相对较大。当护栏透风率小于50%时,积雪会在桥面护栏附近产生沉积,且在迎风端护栏的背风侧(区域2)沉积最严重,最大积雪沉积量约为初始积雪深度(30 cm)的1.25倍。
(3)基于数值模拟结果,建议在桥梁设计时采用高透风率(大于50%)的护栏,以减小风致积雪对桥面交通的不利影响。
