主余震序列作用下边坡位移响应及地震动参数相关性分析

殷京科，李典庆，杜文琪

(武汉大学水资源与水电工程科学国家重点实验室，工程风险与防灾研究所，湖北，武汉 430072)

近年来，我国地震频发，造成了严重的经济损失和人员伤亡。作为我国地震多发地区，西部各省多山地地形，边坡众多。强震作用下，极易造成边坡失稳，从而引发滑坡等次生灾害。据统计，2008年汶川8.0级大地震触发5万余处滑坡，规模较大的包括位于绵竹市安县的大光包巨型滑坡(方量达7.4×108m3)、位于北川县城的城西滑坡(方量达4.8×106m3)，其中城西滑坡导致1600人遇难[1-3]。2010年玉树7.1级地震共触发两千多处中小型滑坡[4]，2013年芦山7.0级地震诱发3800余处滑坡[5]。2013年岷县6.6级地震造成3处大型黄土滑坡，致12人遇难并毁坏房屋100余间[6]。上述灾害后果表明，合理评估边坡在强震作用下的动力响应与滑动位移，对预测地震动的潜在破坏势以及开展快速地震风险评估十分重要。

目前，边坡的地震响应已经得到了国内外研究人员的广泛关注。LENTI和MARTINO[7]通过数值分析，研究了地震波与边坡之间的相互作用对滑坡位移的影响。DU[8]通过数值分析研究了自然边坡在三维地震动输入条件下的滑动位移特征。LI等[9]通过数值模拟研究了土体参数空间变异性对地震边坡滑移风险的影响规律。王斌等[10]通过振动台试验研究了地震作用下的岩质高陡边坡的加速度响应规律及破坏形式。李典庆等[11]基于子集模拟提出了一种用于边坡风险分析的高效随机有限元方法。张泽林等[12]针对西北地区的黄土泥岩边坡的动力响应和破坏特点展开研究。WANG等[13]分析了黄土层厚度及坡度对边坡放大效应的影响。ZHAO等[14]通过振动台试验对随机地震作用下的边坡动力响应展开研究。WANG 等[15]通过有限差分法对地震动幅值和持时对分层边坡动力响应的影响开展了深入研究。通过上述边坡地震响应分析的相关研究，研究人员对地震作用下的边坡响应大小以及相应的损伤演化特征有了较为全面地认识。

一次地震的发生往往伴随有多次余震的发生。2008年汶川大地震发生后两个月内，触发了20 000多次余震，其中包括数十次震级大于五级的强余震[16]。2013年芦山地震过后的三天内，发生余震高达3000余次，震级大于五级的余震大约有四次[17]。余震是由能量未释放完全的主震断层或者临近断层的破裂产生，因此余震与主震在发震时间和空间位置分布上存在一定的相关性，而主余震的时空分布特性对工程结构的动力响应也有较大影响。因此，有必要对主余震联合作用下的边坡响应进行有效评估。事实上，目前针对建筑结构在主余震作用下的损伤已经得到了研究人员的关注，且较多关注“主震+最大震级余震”作用下的动力响应。例如：朱瑞广等[18]通过振动台试验研究了真实主余震序列作用下的非延性框架的动力响应，并指出主余震序列的频率特性与结构损伤存在较为密切的联系。于晓辉等[19- 20]通过对主余震序列作用下的结构损伤进行计算，发现部分余震会使结构产生显著增量损伤，并且对比了采用不同主余震构造方法得到的人工主余震序列作用下的结构损伤。ZHOU 等[21]对地震动强度参数与主余震作用下的结构损伤的相关性进行了分析，并建立了基于最优参数的主余震损伤预测模型。周洲等[22]通过研究主余震作用下的结构增量损伤比来定量评估余震对结构损伤的影响。韩建平和李军[23]对主余震作用下的低延性结构进行了易损性分析。申家旭等[24]基于Copula 理论建立了能够较好表示序列地震空间相关性的序列型地震动随机模型。然而，目前国内外对边坡在主余震序列作用下的响应特征研究还较少。其中，陈金昌[25]对边坡在人工主余震序列作用下的加速度响应和横向位移做了初步分析。然而，该研究采用了重复法构造人工主余震序列，无法真正反映真实主余震序列的特征，也无法真正考虑主震和余震强度之间的相关性，致使分析结果无法真实反映余震对边坡动力响应的影响。由于对边坡在主余震序列作用下的响应研究不足，使得研究人员无法真正掌握边坡在发生主震损伤后进一步遭受余震作用时的安全性。

为解决目前对边坡的主余震响应研究较少的问题，本文从太平洋地震工程研究中心的NGAWest2强震数据库筛选了210条真实主余震序列，基于有限差分软件FLAC对主震单独作用下和主余震序列作用下的边坡位移响应进行数值模拟，针对余震对坡肩的竖向永久位移的影响进行定量分析。基于已获得的边坡主余震的位移响应，对边坡竖向永久位移与15个地震动参数的相关性展开研究，选取最优参数并建立考虑余震效应的边坡主余震位移的预测模型。

1 主余震序列的挑选与构造

鉴于主余震的发生机理与时空分布特性非常复杂，本文未考虑主-余震的空间相关性对边坡动力响应的影响，而是直接挑选真实主余震序列作为地震输入来分析边坡响应。通常一次强主震之后会发生多次余震，本文在构造真实主余震序列时仅考虑具有最大震级的余震，即一条主余震序列包含一次主震和一次最大余震。本文基于太平洋地震工程研究中心的NGA-West2强震数据库进行主余震序列地震动挑选，主要依据如下：1)为了获得较明显边坡位移响应，选择矩震级Mw大于6.5的主震；2)主震和余震的记录台站位于自由场地或者较低矮的结构；3)用于构造真实主-余震序列的主震地震动和最大震级余震地震动须由同一台站记录，避免台站的位置差异对主余震地震动相关特性的影响；4)场地的平均剪切波速VS30不小于100m/s。根据上述挑选原则，挑选获得了210组主震和余震记录，它们分别来自8个地震事件。各个地震事件的基本信息(震级及发生时间等)如表1所示。图1给出了所挑选主余震记录的震级与断层距分布情况。由图可见：断层距离在0 km～250 km，主震和余震的震级差大约为1级，基本满足Bath 定律[26]。

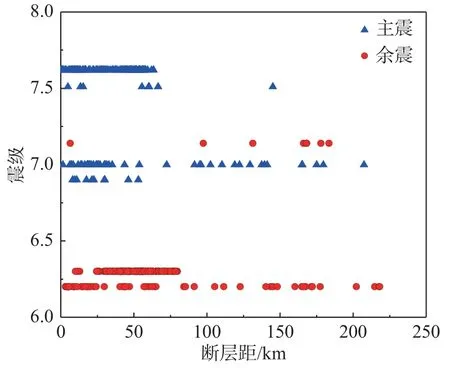
图1 挑选的主、余震记录的震级和断层距分布Fig.1 Distribution of magnitude and rupture distance of the selected mainshock and aftershock records

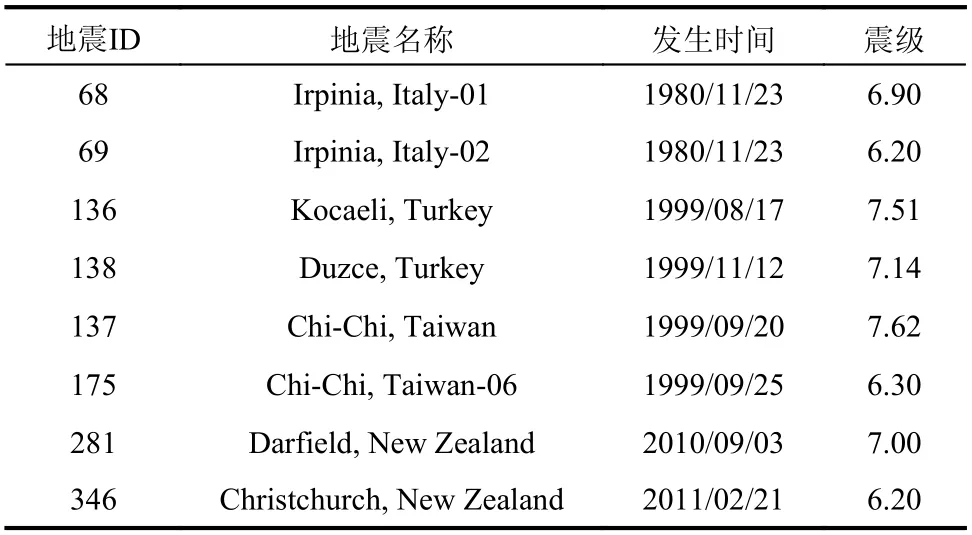
表1 挑选主、余震地震动的地震事件基本信息Table 1 Detailed information of selected mainshock and aftershock events

基于所挑选的主余震记录计算它们的反应谱，并分别给出具有97.5%、50%和2.5%分位值的反应谱曲线，如图2所示。对比主、余震记录的反应谱可以发现：在图示任意自振周期处，主震的反应谱中位值大于余震的反应谱中位值，证明了主震强度普遍高于余震强度。基于所挑选的主余震地震动，采用主震+100 s间隔+余震的形式来构成主余震序列[19]。图3给出了一条典型主余震序列加速度时程。该序列中主震和余震在NGAWest2数据库中的序列号分别为292和303，选自于Irpinia 地震事件。采用上述方法所构成的210条序列型地震动将用于主余震序列作用下的边坡位移响应分析。

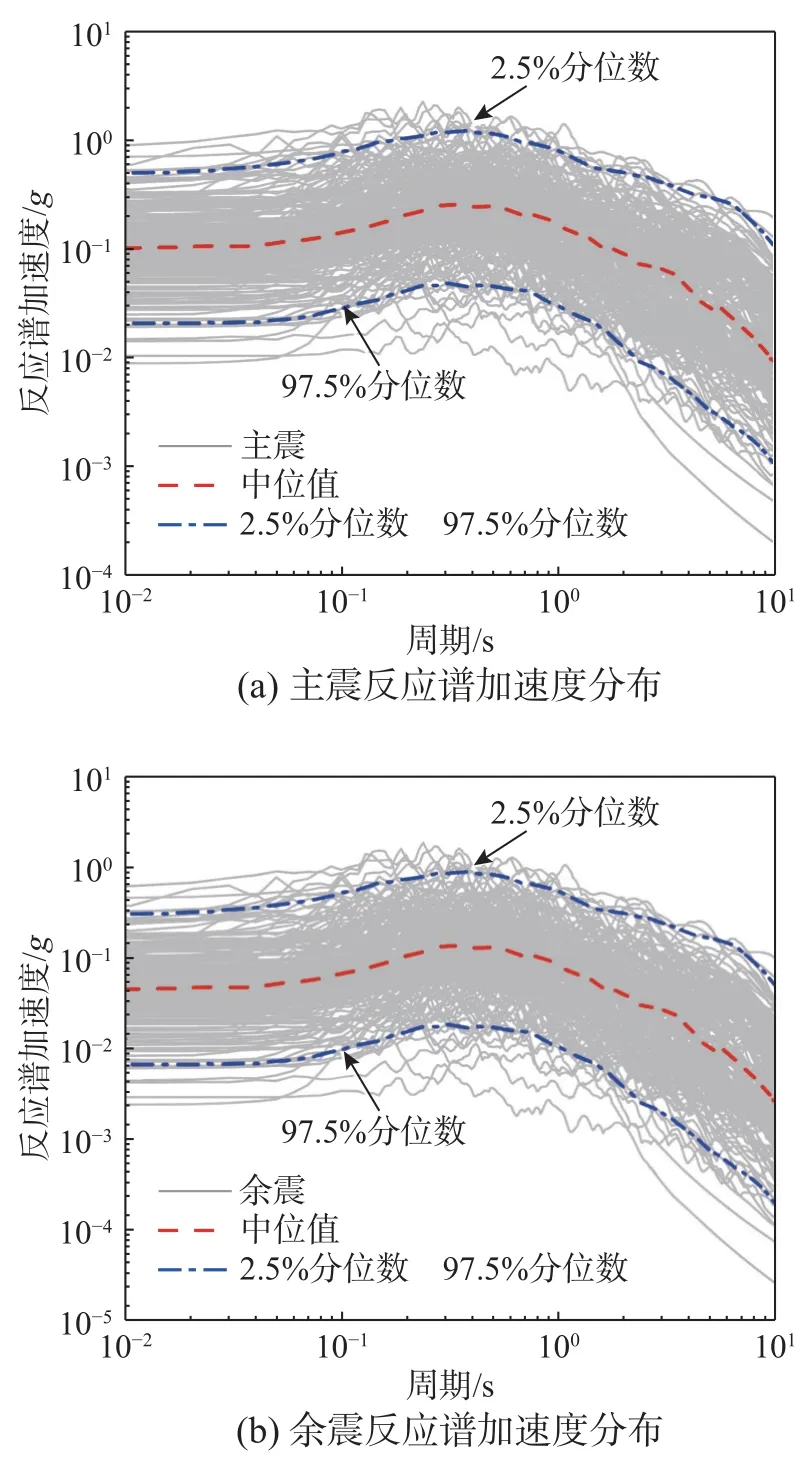
图2 主震和余震反应谱加速度曲线Fig.2 Response spectra of mainshock and aftershock ground motions

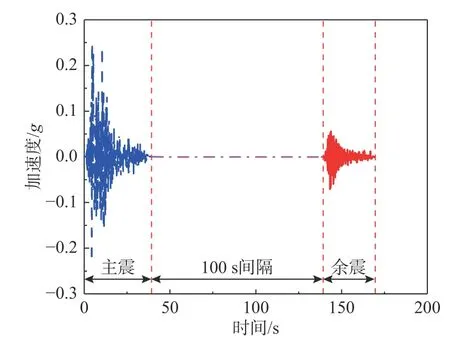
图3 典型主余震序列加速度时程Fig.3 A typicalmain-aftershock acceleration sequence

2 多层边坡动力响应分析模型

本文基于有限差分软件FLAC，采用WANG 等[15]提出的多层边坡建模方法来分析边坡在主余震序列作用下的响应。自然边坡中土体呈层状分布，不同深度土体的密度和模量参数不同。与均质边坡模型相比，分层边坡更能反应土体的成层特性，从而得到更准确的动力响应。图4为WANG等[15]建立的典型多层边坡模型。模型尺寸为：长150 m×高30m。各层岩土体的材料参数如表2所示。

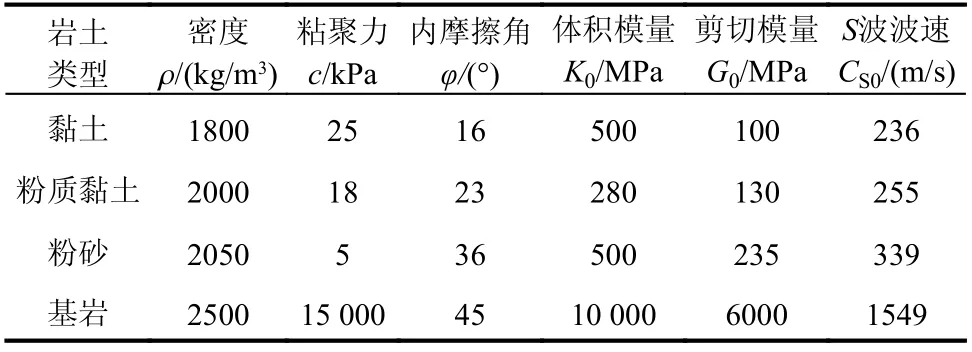
表2 边坡模型中各土层材料参数Table2 Material parameters of each layer in the slope model

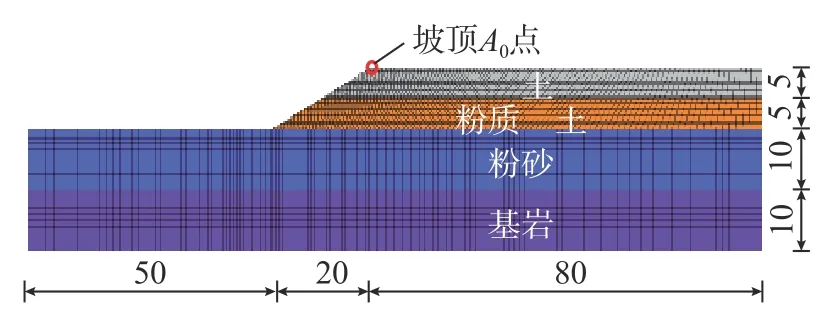
图4 多层边坡模型的几何尺寸与网格划分/m Fig.4 Geometric property and grid size of the slope model

采用摩尔-库伦塑性本构模型来模拟土的非线性特征。模型的网格尺寸与计算结果的准确性以及计算时间的长短紧密相关。本文在确定模型的网格尺寸时，考虑以下两方面要求：1)地震波传播的数值精度会受到输入地震波的频率成分和土体剪切波速的影响，为了更为准确的模拟地震波的传播过程，网格尺寸ΔL须小于输入地震波最高频率对应波长的1/8～1/10[27]；2)在动力分析中还应考虑由于模量衰减引起的横波速度的变化，特别是对于潜在滑动区域内的网格单元。根据经验剪切模量衰减曲线，取剪切模量衰减系数为1/16(1%～10%的应变范围内)[28]。综上，确定本文边坡模型的网格尺寸ΔL为0.5 m～1.8m，其中潜在滑动区域的网格尺寸约为0.5 m。

岩土体内部的摩擦会导致部分能量的耗散，通常用力学阻尼来描述量化这一特性。本文通过设置阻尼比为0.2%的瑞利阻尼刚度分量来过滤高频噪声，同时设置由Hardin-Drnevich 模型[29]拟合的滞后阻尼(参考应变取0.234)，模拟岩土体在循环加-卸载过程中的模量衰减和能量耗散。在设置瑞利阻尼时，用模型自振频率代替中心频率，通过边坡模型的自振分析，得到边坡模型自振周期为0.25 s，自振频率为4Hz。

采用多层边坡模型分析边坡的地震响应分析主要分为两个阶段：1)重力施加阶段，将两侧边界沿法向约束，将底部边界沿X、Y方向约束，对边坡单独施加重力，提取整个边坡模型的初始应力分布；2)动力响应分析阶段，将两侧边界设置为自由场边界，减少边界上波的反射，并将底部边界X向的约束解除。在底部边界的节点上沿X方向施加地震波速度时程，计算边坡的动力响应，获得坡顶A0处(坡肩)的竖向位移响应。

3 边坡的主余震位移响应

边坡的竖向永久位移是评估其稳定性的重要参数，其可以较好地描述边坡在地震作用下的损伤状态。为了评估余震对边坡位移响应的影响，分别对边坡在主震单独作用下和主余震序列作用下的竖向永久位移响应进行分析和对比。为此，本文提出一个无量纲参数“位移增量比δD”来定量评估余震对边坡位移的影响：

式中：DM和DMA分别为主震和主余震序列作用下的边坡竖向永久位移；ΔDA表示由余震造成的边坡竖向永久位移增量。

选择图4所示这一典型边坡作为研究对象，该边坡坡高为10m，边坡水平长度为20m，坡比为1∶2，边坡从上到下由黏土层(厚度5m)和粉质黏土层(厚度5m)构成；边坡底部地基从上到下由粉砂层(厚度10 m)和基岩层(厚度10m)构成。浅层土体密度和模量较小，且土体密度和模量随深度增加而增大。上述边坡条件基本符合自然边坡中的土层分布情况。为了降低左侧和右侧边界对地震波传播的影响，坡顶到右侧边界的距离设置为80 m，坡脚到左侧边界的距离设置为50m。采用第2节中的多层边坡动力分析模型，分析获得该边坡在第1节中所挑选的210条主余震序列输入下的竖向永久位移。图5给出了在一条主余震序列作用下竖向永久位移变化曲线，可以发现主震损伤边坡在遭受继发余震作用后，产生了明显的竖向位移。

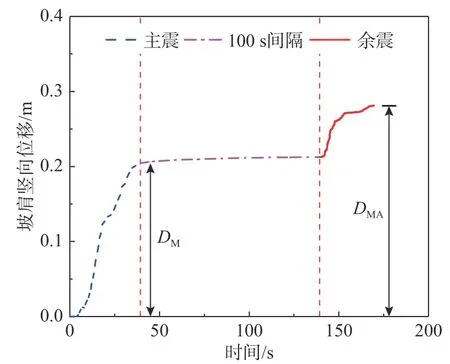
图5 主余震序列作用下坡肩竖向位移累积曲线Fig.5 Accumulation of verticaldisplacement at slope crest induced by a main-aftershock sequence

图6给出了计算获得的DM和DMA分布情况。由图可见，主余震序列作用下的边坡竖向永久位移DMA最大值约为1m，最小值约为10-6m。主震损伤边坡在余震作用下，最大位移增量ΔDA=0.47 m。对于68.6%的主余震序列，DMA大于DM。由此可见：主震损伤边坡在遭受余震之后会产生一定的增量位移。进一步对这部分主余震序列造成的竖向永久位移增量ΔDA和位移增量比δD进行统计分析，ΔDA和δD分布情况如图7和图8所示。29.6%的余震作用下产生的位移增量满足ΔDA≥0.001 m，可认为余震能够造成边坡竖向永久位移一定程度的增大。此外，在所挑选的真实主余震序列中，40.0%的主余震序列作用下的边坡位移增量比δD大于10%且小于100%，可认为余震对边坡位移的影响显著。另外，有6.2%的主余震序列所造成的边坡位移增量比δD大于100%。

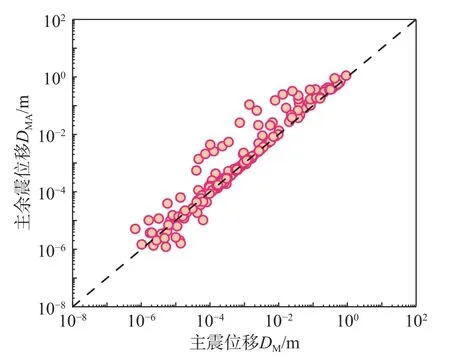
图6 边坡竖向永久位移D M 和D MA 分布Fig.6 Vertical permanent displacements D M and D MA of slope

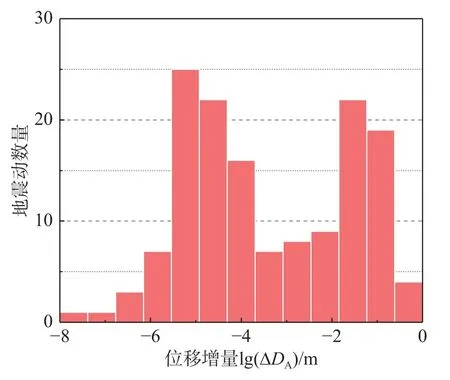
图7 位移增量分布柱状图Fig.7 Distribution of the incremental displacements

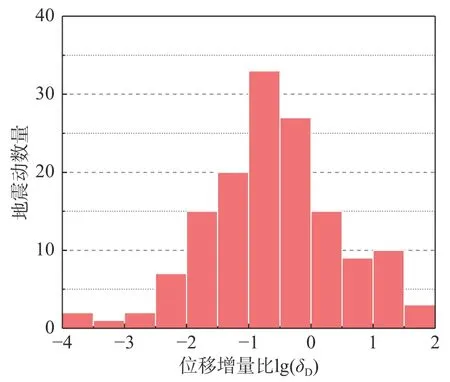
图8 增量位移比分布柱状图Fig.8 Distribution of the incremental displacement ratios

4 边坡的主余震位移响应与地震动强度参数相关性

4.1 地震动强度参数

在第3节研究的基础上，进一步研究地震动强度参数IM与边坡竖向永久位移D的相关性。本文挑选了15个地震动强度参数作为备选参数。其中，包括：六个加速度相关的IM(PGA、Sa(Ts)、Sa(1.5Ts)、IA、ARMS、ASI)、三个速度相关的IM(PGV、VRMS、VSI)、两个位移相关的IM(PGD、DRMS)以及其他四个IM(Ds5～75、Ds5～95、Tm、Tp)。上述所挑选的地震动强度参数的信息，如表3所示。分别采用下标M 和A 表示主震和余震。值得说明的是，本文主要研究的是主余震序列强度与边坡位移响应的相关性。分别采用主震强度、余震强度和余震和主震强度比作为主余震序列的强度参数指标。举例而言，对于峰值加速度PGA来说，分别采用PGAM、PGAA和δPGA表示主震PGA、余震PGA、余震和主震PGA强度比。

表3 挑选的地震动强度参数Table 3 Selected ground motion intensity measures

4.2 相关性分析

在地震危险性分析中通常假设地震动强度参数(例如：PGA、Sa等)近似服从对数正态分布[30]。为了研究地震动强度参数与边坡位移的相关性，本文在对数空间上分别计算了下述五种相关系数：1)主震强度与边坡主震位移(相关系数ρ1)；2)余震强度与边坡余震增量位移(ρ2)；3)主震强度与边坡主余震位移(ρ3)；4)余震强度与边坡主余震位移(ρ4)；5)余震主震强度比与边坡位移增量比(ρ5)。

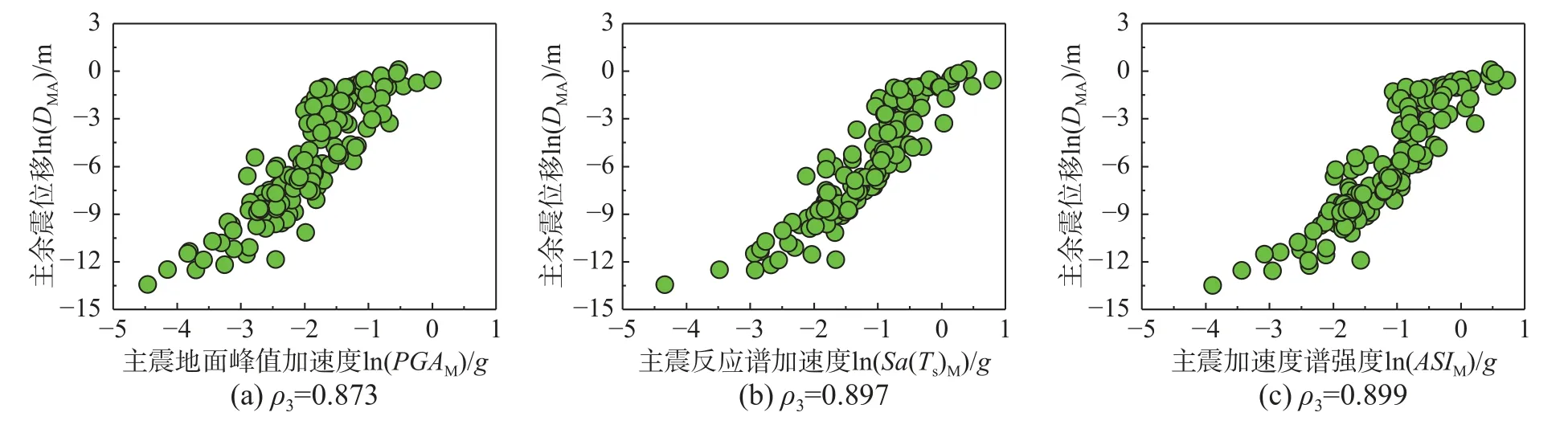
图9给出了15种地震动强度参数所对应的上述五种相关系数值。由图可见，加速度相关的IM(PGA、Sa(Ts)、Sa(1.5Ts)、IA、ARMS、ASI)、速度相关的IM(PGV、VRMS、VSI)以及位移相关的IM(PGD、DRMS)与位移参数呈正相关，且加速度相关的IM与位移参数的相关性相对较强；另外四个IM(Ds5～75、Ds5～95、Tm、Tp)与位移参数呈负相关。这是因为地震动强度越大，引起的边坡永久位移越大，且地震能量集中在较短时间释放，会造成更大的永久位移。与主震位移DM相关性最强的三个主震强度参数分别为Sa(Ts)M、ASIM和PGAM；与余震增量位移ΔDA相关性最强的三个余震强度参数分别为ASIA、Sa(Ts)A和PGAA；以上六组参数与位移的分布如图10所示。由图10可以看出：主震强度参数与主震位移、余震强度参数与余震增量位移都有较强的相关性，但是后者稍弱于前者。其原因是：主震损伤状态对余震增量位移产生了影响，一定程度上削减了余震强度参数与余震增量位移的相关性。与主余震位移DMA相关性最强的三个主震强度参数分别为ASIM、Sa(Ts)M和PGAM，与主余震位移DMA相关性最强的三个余震强度参数为ASIA、Sa(Ts)A和PGAA，与位移增量比δYDis相关性最强的三个余震主震强度参数比为δASI、δSa(Ts)和δPGA，以上九组参数的分布如图11所示。由图11可以看出：在ρ3、ρ4、ρ5这三种相关系数中，位移增量比与余震主震强度参数比的相关系数最小，主余震位移与主震强度参数的相关系数最大，主余震位移与余震强度参数的相关系数介于两者之间。其中，主震反应谱加速度Sa(Ts)M和主震加速度谱强度ASIM与主余震位移的相关性最强。

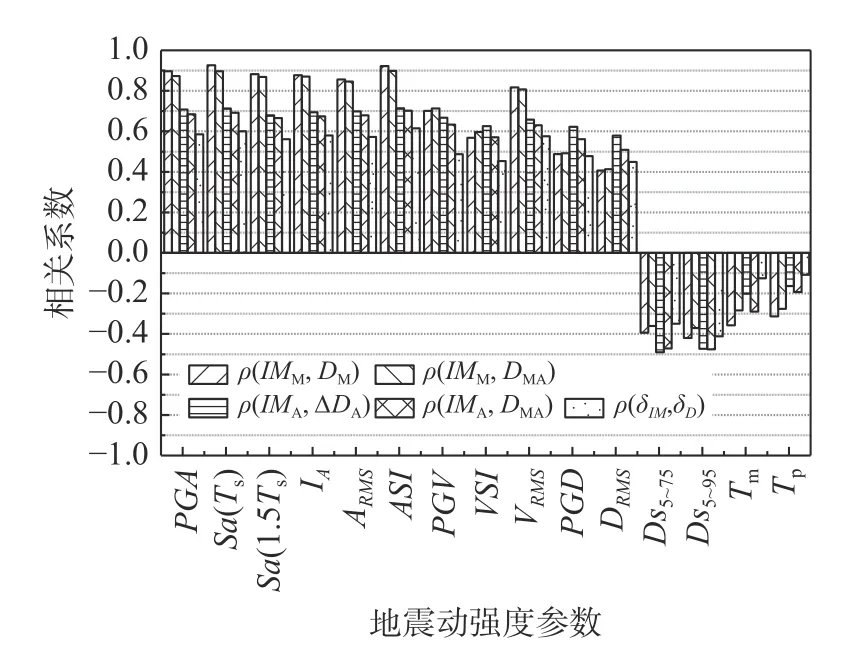
图9 不同地震动强度参数与边坡竖向位移的相关系数Fig.9 Correlation coefficients between different ground motion intensity measuresand the settlement of slopes

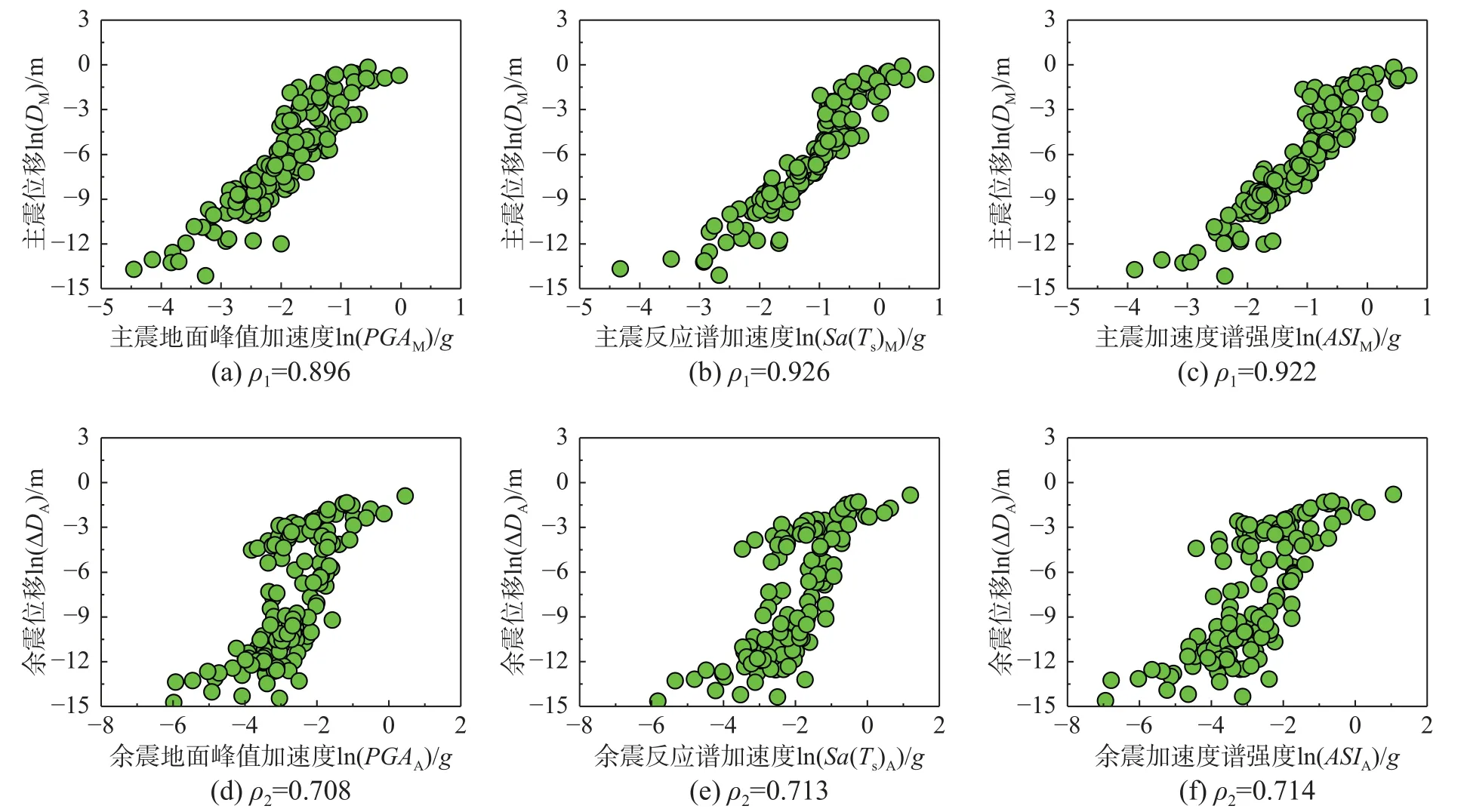
图10 主震和余震强度参数与边坡竖向位移(D M 和ΔD A)的相关性分布Fig.10 Correlationsbetween intensity measures of mainshocks and aftershocksand the permanent settlements(D M and ΔD A)of slopes

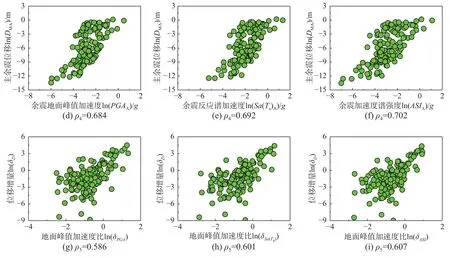
图11 主余震强度参数与边坡竖向位移(D MA 和δD)的相关性分布Fig.11 Correlations between intensity measuresof main-aftershocksand the permanent settlements(D MA and δD)of slopes

4.3 边坡主余震响应的预测

在上述相关性研究中，共探讨了三类主余震强度参数与位移参数的相关性，结果表明：主震强度参数与边坡主余震位移的相关性最强。基于筛选的两个最优地震动强度参数Sa(Ts)M和ASIM，通过最小二乘回归方法，建立两个主余震位移预测模型(对数线性)。如图12所示，所提出的位移模型能够较好地描述数值模拟的结果。在已知主震反应谱加速度或主震加速度谱强度的情况下，可对主余震作用下的边坡坡肩竖向永久位移DMA进行预测。需要指出的是，本文所建立的主余震位移预测模型仅针对算例边坡，若边坡土体参数或边坡尺寸改变时，上述模型参数也应相应修改。

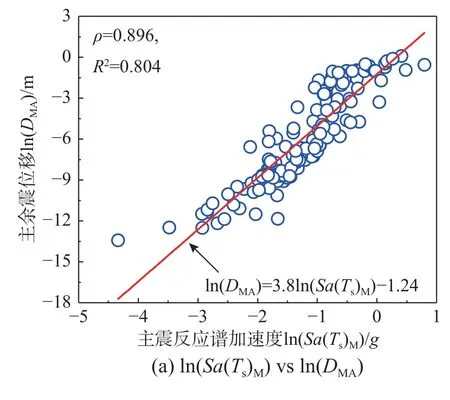
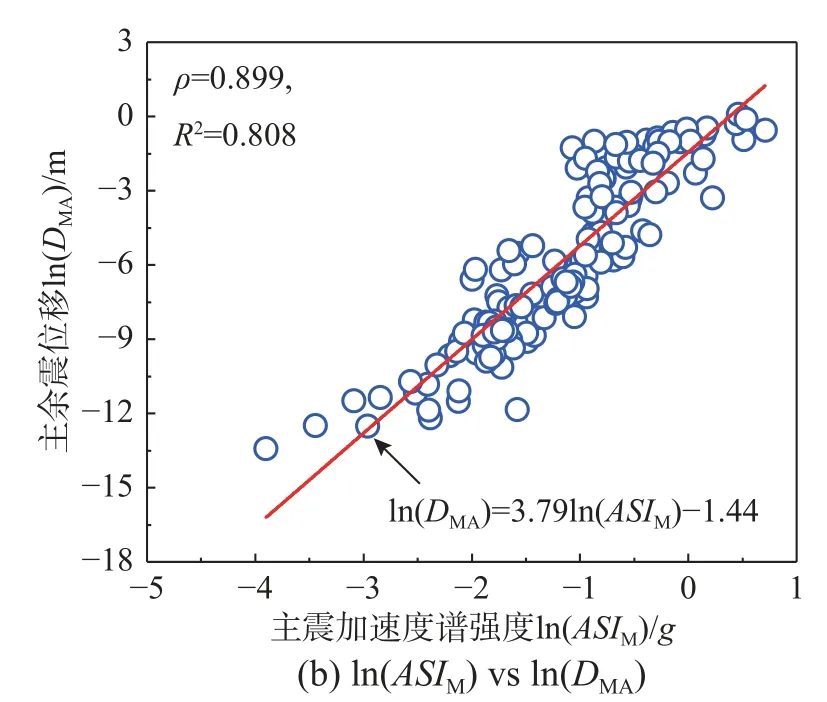
图12 基于最优地震动强度参数的主余震竖向位移预测Fig.12 Predictive model for vertical permanent settlement of slopes based on optimal IM saspredictors.

5 结论

本文通过对边坡在真实主余震序列作用下的大量位移响应进行分析，对余震对边坡位移的影响开展了评估研究，同时探讨了采用不同地震动参数表征的主余震序列强度与边坡位移响应的相关性，得到如下结论：

(1)余震会对主震损伤边坡产生较为明显的增量损伤。在所挑选的210条真实主余震序列中，40.0%的主余震序列造成的位移增量比大于10%且小于100%；6.2%的余震作用下产生的位移甚至大于主震位移。

(2)主余震序列强度与边坡主余震位移的相关性分析结果表明：主震强度与边坡主余震位移的相关性最强。在所考虑的地震动强度参数中，与主余震位移参数相关性最强的两个参数为主震反应谱加速度Sa(Ts)M与主震加速度谱强度ASIM。

(3)根据主余震序列强度与典型分层边坡主余震位移的相关性，建立了两个主余震位移预测模型，可以较好地预测算例边坡的主余震位移响应。

本文的相关结果通过本文算例边坡计算获得，但相关规律并不局限于此算例边坡，其同样适用于其它具有不同几何尺寸和土体参数的边坡工况。由于地震序列本身的复杂性和边坡动力响应的强非线性，对于边坡的主余震反应特性还需要进一步深入研究来考虑不同场地条件、边坡类型、土体参数等对边坡位移结果的影响。此外，还需要开展一系列物理模型试验研究，以加深对边坡在主余震作用下破坏过程及其破坏机理的认识。