大尺度类波形壁面湍流边界层TR-PIV实验研究

唐 俊，闫一天，刘岩岩

大尺度类波形壁面湍流边界层TR-PIV实验研究

唐 俊1, 2，闫一天1, 2，刘岩岩1, 2

(1. 天津大学建筑工程学院，天津 300350；2. 天津大学港口与海洋工程天津市重点实验室，天津 300350)

针对传统波形壁面因尺度微小所引发的加工困难、维护费用昂贵等问题，设计了一种大尺度的类波形壁面．对虎鲸的皮肤嵴结构进行放大和形貌改良，得到的大尺度类波形壁面可以更好地适用于工程实际；研究了大尺度类波形壁面对湍流边界层的影响，分析了其减阻效果及减阻机理．采取高时间分辨率粒子图像测速(TR-PIV)技术，对光滑壁面和振幅与波长之比分别为21/＝0.033、22/＝0.050、23/＝0.066的3种大尺度类波形柔性壁面湍流边界层流场进行了实验测量，对流场中的时空相关函数进行计算．分析一个波长范围内流向、法向速度及压力分布，发现波形结构下坡段附近的逆压梯度使得流动减速，爬坡段附近的顺压梯度则加速了流动，减速效果最强位置位于波谷，加速效果最强位置位于波谷始末，流场中的速度在两个极值内变化．对不同工况下类波形壁面末尾凹槽下游紧邻平板区域各阶统计量进行了对比，结果表明3种类波形壁面的平均速度剖面于对数区表现出不同幅度的抬升，近壁区平均速度均有不同程度增大；近壁区流场雷诺切应力具有明显的降低，近壁区湍流脉动被抑制，雷诺应力的峰值相对壁面略有外移；3种类波形壁面均具有一定减阻效果，最大减阻率为23.0%．

波形壁面；湍流；高时间分辨率粒子图像测速；雷诺应力；减阻；仿生

摩擦阻力与压差阻力是流体阻力最基本的两种形式，固体与流体之间的相互作用以及流体分子间吸引力形成了壁面阻力．多年来对湍流边界层的实验和模拟[1-3]表明，一系列的自维持运动发生在近壁面湍流边界层中．对湍流运动的研究[3]发现，80%的湍流动能都是由于喷射和扫略两个事件产生．扫略事件与壁面剪切应力的出现紧密联系，一般发生在近壁+≤15处[4-5]，因此，对固体壁面进行形貌改造设计成为一种直接且有效的减阻手段．

早在20世纪70年代，对于波形壁面的研究逐渐兴起[6]，之后，学者针对正弦波壁上的流动特性进行了实验和数值研究，Wagner等[7]探究了在波浪壁上完全发展的湍流中同时测量速度场和浓度场的方法，提出由平面激光诱导荧光技术(planar laser-induced fluorescence，PLIF)获得浓度场的瞬时状态，速度场则由数字粒子图像测速(digital particle image velocimetry，DPIV)评估．Nakagawa等[8]在研究中假设壁面完全粗糙，测量了正弦波边界上垂直于壁面的平面速度场，结果表明，尽管壁面维持湍流的机制完全不同，正弦波壁面近壁湍流结构与光滑表面上的情况类似．Hamed等[9]对波形壁面的PIV测量表明，正弦波壁面上方形成了回流区，沿湍流剪切层产生高湍流强度．Calhoun等[10]采用大涡模拟方法研究了波形壁面上稳定分层的湍流流动，通过条件取样，分析了主要的雷诺应力事件，结果表明最强的雷诺应力发生在波谷上方大约波峰高度位置，该区域中喷射主导了扫荡，喷射事件的平均幅度较大．王维等[11]通过象限分裂法探究了波形壁面湍流相干结构，提出喷射事件有着相对较低的发生概率，但对于雷诺应力的贡献量大于扫略事件，强调了喷射事件的主导作用．葛铭纬[12]通过直接数值模拟研究了充分发展的槽道湍流中上下对称的波形壁面，指出展向振荡下的流动具有明显周期特性，在+＜5的波形幅值下，近壁湍流得到抑制，实现了减阻．Vlachogiannis等[13]研究的波形壁含有600个波长为5mm、振幅为0.25mm的正弦波，探究了两种不同雷诺数流场的紊流强度与距壁面无量纲化距离的关系．Yamagata等[14]在对正弦波形壁面的研究中观测到波形面壁面上的流动分离和再附着，在再附着区域观察到了湍流能量的增加，同时指出波形壁面上相对粗糙度(深宽比)的增加导致分离的提前和再附着的延迟，这导致回流区的增加和波谷上方回流区高湍动能的产生．前人的研究对波形壁面上流场特征进行了总结，为之后的研究提供了理论参考，但微小尺度的波形壁在工程实际上面临加工困难、维护成本高等问题，之前的研究缺少对相关问题的针对性探讨．本文研究一种大尺度类波形壁面，旨在提升波形壁减阻在工程实际上的可行性，研究新型的类波形壁面流场特征，并对其在减阻性能方面展开研究．

本文以湍流边界层内各阶统计量为主要分析对象，利用高时间分辨率粒子图像测速(time-resolved particle image velocimetry，TR-PIV)技术，对带有光滑平板间断的半正弦波形壁面(后称类波形壁面)的减阻机理进行了实验研究：选取虎鲸皮肤嵴结构作为仿生来源，在基础上进行放大和形貌改良得到3组振幅波长比的类波形壁面；测量了一个波长范围内壁面流场压力与速度变化趋势，对类波形壁面末尾波形单元下游紧邻光滑平板区域的一、二阶统计量进行观测与分析，从而探究类波形壁面湍流边界层内流场特征，分析其减阻性能与机理．本研究为适用于工程实践的壁面减阻技术提供思路与参考．

1 实验设备和技术

TR-PIV实验在天津大学流体力学实验室开口式循环水槽中进行．水槽实验段长度为620cm，内壁截面积为25cm×38cm(宽×高)，流速在60cm/s以下连续可调．实验段整体由玻璃板构成，在测量区域内设置了一个与水平面刚好贴合的玻璃盖板，以实现高流速下PIV的无干扰测量．在自由来流速度＝48cm/s的情况下，测得流场背景湍流度为0.7%．实验时水温保持在20℃，在该温度下水的密度＝997.78kg/m3，运动黏度＝0.97937×10-6m2/s．实验水槽结构与实验现场如图1所示．

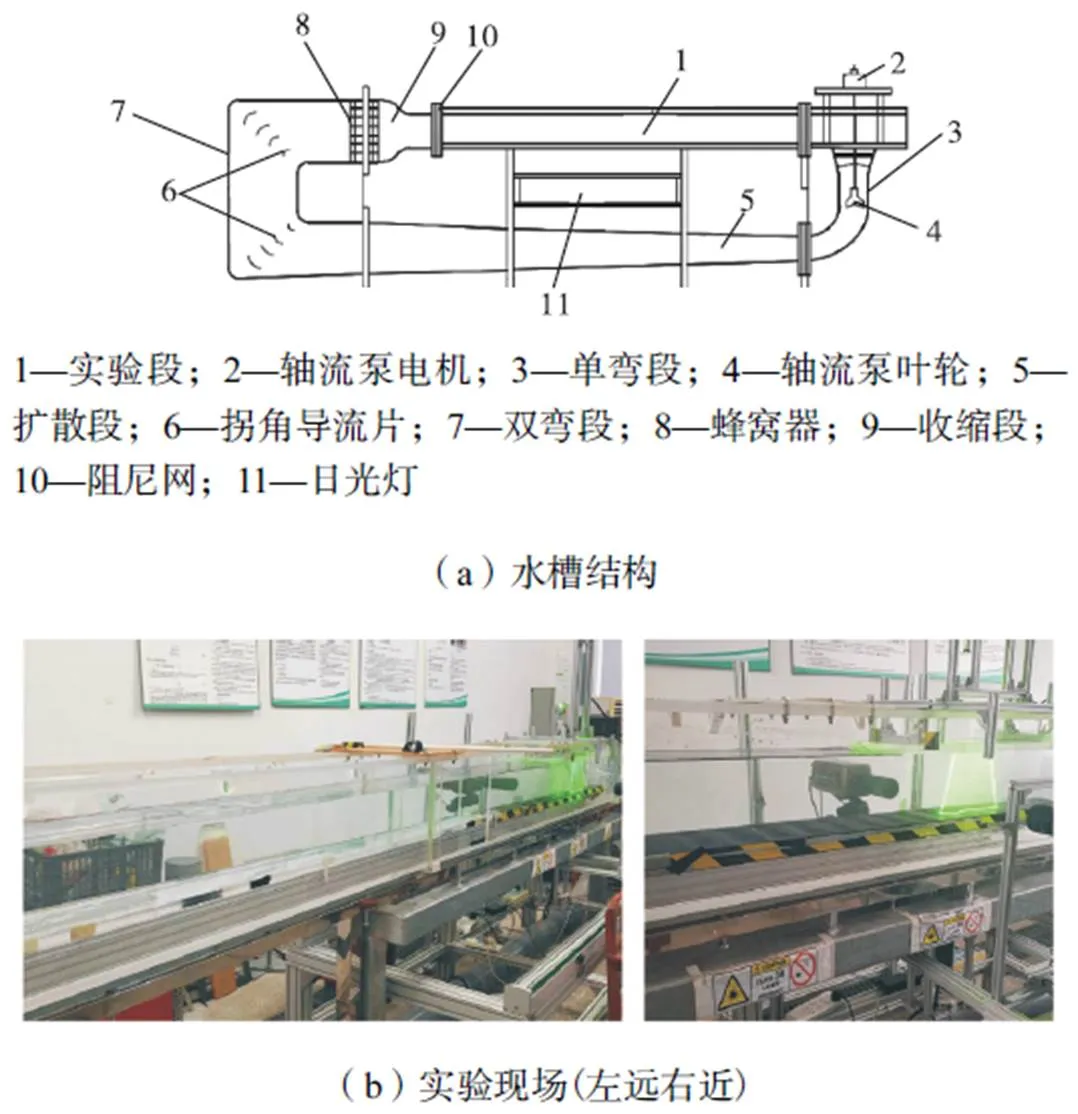
图1 水槽结构与实验现场

1.1 实验模型设计

类波形壁面减阻的理念源于对虎鲸、海豚皮肤嵴结构的研究，虎鲸等齿鲸亚目类动物身体大部分皮肤表面分布着波纹状的规则皮肤嵴．根据组织切片和环氧树脂模具的显微镜测量，皮肤嵴相邻峰间距为0.41～2.35mm，嵴的高度为7～112μm[15]．虎鲸的皮肤嵴在皮肤表面近乎垂直于流向分布，类似于随行波，如图2所示[16]．然而皮肤嵴尺度微小，直接用于工程实际难度较大．因此，参照虎鲸皮肤嵴形状特征，即约为0.05的振幅波长比，依照前期仿真结果对皮肤嵴截面曲线放大40倍，将原本粗糙的皮肤嵴截面曲线光顺为简易几何线，基于水下航行器表面工程设计需求与仿生原理，提出一种新型的类波形壁面，剖面曲线如图3所示．其中，为实验板上水平方向坐标，为垂直方向高度，为类波形结构的波长，1～3为3种类波形壁面的振幅．

应用于水下航行器的壁面减阻技术研究中，微小尺度的壁面减阻结构对加工工艺的要求高，制造成本高，同时，减阻壁面在海洋环境中的减阻性能不可避免地受到污物附着的影响，微小尺度的壁面减阻结构被污物掩盖后会迅速失效．在本研究中，大尺度的设计提升了类波形壁面对污物附着的耐受力，与微小尺度的壁面减阻结构相比，等量的污物附着对类波形壁面减阻效果的影响较小，需要相当程度的污物附着才可以改变类波形壁面形貌的整体趋势，因此，为维持航行器表面减阻结构性能而展开的壁面清洁作业的间隔更长，同时清洁单位面积表面的耗时更短；另外，类波形壁面的壁面结构简洁且强度更好，工程安装作业的难度更低．综上，相较微小尺度的非光滑壁面减阻结构，类波形壁面更加适用于工程实际．

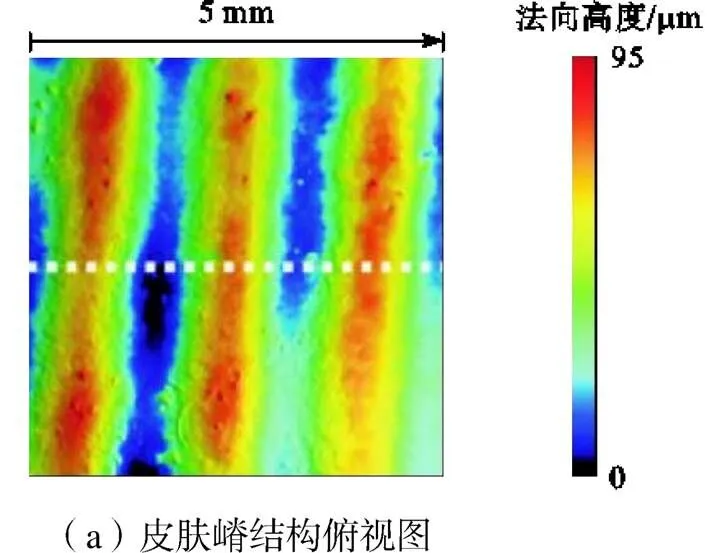
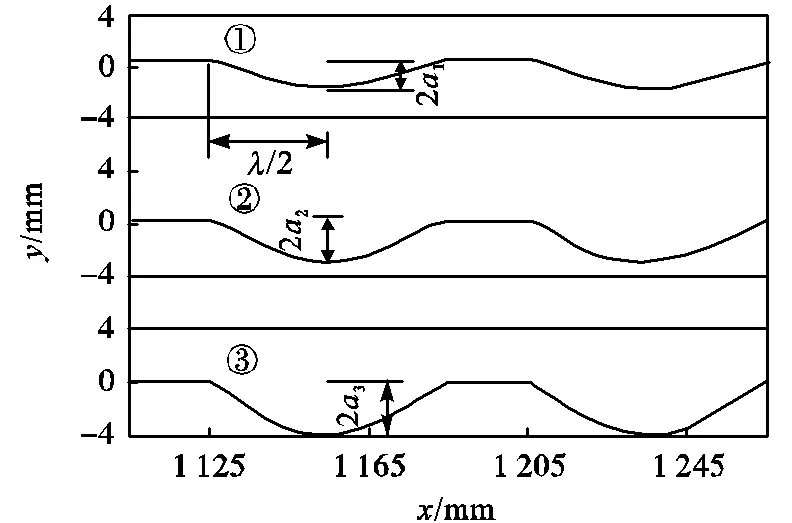
图3 类波形壁面剖面曲线

类波形壁面的截面曲线为虎鲸皮肤嵴曲线经过等比例放大之后光顺得到，满足几何相似，并考察了小范围振幅波长比变化对流场的影响，类波形壁面的3个振幅取值均小于边界层厚度[17]；为了符合动力相似的要求进行了雷诺数的估算，以虎鲸游动速度范围作为推算条件，假设约为8～15m/s，特征长度为虎鲸表皮皮肤嵴间距，设为2mm，水温为20℃的黏度为0.001Pa·s，海水密度为1025.5kg/m3，计算得到虎鲸游动时的表皮流场雷诺数在16～3.1×104范围内，实验中，来流速度设置为∞＝0.48m/s，取类波形壁面波长60mm为特征长度，计算得到雷诺数约为2.8×104，处于虎鲸游动时表皮流场雷诺数范围内．

实验模型由两段板紧密拼接而成，按照来流方向，置于上游的板为前缘按8∶1的比例进行修型的光滑玻璃平板，宽252mm，长1.5m，以确保实验段为充分发展的湍流边界层，另有3块特殊设计的贴皮铝合金板作为后侧实验板，铝合金板表面贴附光滑橡胶柔性层，实验板中央有10个均匀排布的正弦波展向沟槽，铝合金板贴皮后模拟的3种类波形壁面振幅与波长之比分别为21/＝0.033、22/＝0.050、 23/＝0.066，波长均为＝60mm，整板宽252mm、长1600mm，中央类波形凹槽区域前后各有410mm长平板区域，经过调整使两块板上表面距水槽底部56mm放置．

1.2 实验测量技术

实验测量了充分发展湍流边界层中的流-法向()平面，激光片光源与来流方向平行，从水槽的上方垂直于平板照亮平板中心区域，设置两台高速相机，光轴与片光垂直，分别用于拍摄类波形壁面末端凹槽及紧邻该凹槽后端的平板区域，相机置于水槽两侧，布置如图4所示．

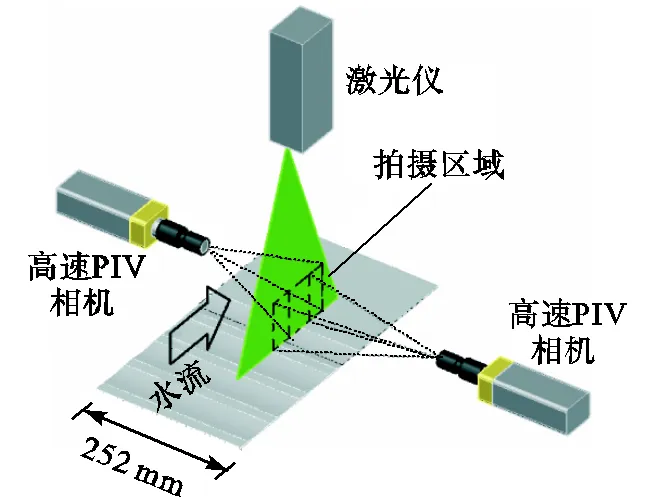
图4 实验装置布置图

利用Dantec公司的TR-PIV系统，在来流速度为0.48m/s的流速下，对不同壁面的湍流边界层进行了实验测量．相机设定连续拍摄模式，分辨率为1280像素×1024像素，粒子图像的物理范围为145mm×82mm. 粒子在图像上的平均直径p约为2个像素，可以忽略相关峰值锁定影响(peak-locking effect)．每个试验工况下进行持续12.8s拍摄，各记录8215张图像，各工况拍摄前会静待1min以确保流场发展至稳定，为方便统计分析，每种工况各进行了两次重复拍摄记录，两次测量结果仅存在1%左右测量误差[18]．

按照下列步骤对原始图像进行处理．

(1) 通过背景消除法除去背景噪声，去除由于实验板反光带来的测量误差．

(2) 在适当的查询窗口和重叠率下进行“自适应互相关”运算，得到初始的速度矢量场．

(3) 对矢量场进行“上下限过滤”和“平均过滤”处理，去除速度场的噪声，最终得出瞬时速度场．自适应互相关计算过程中，依照图像中粒子的位移，选取平面中查询窗口尺寸为36像素×32像素，重叠率为75%，最终所得到的每张瞬时速度场中包含158×98(流向×法向)个矢量．

2 一个波长范围内的流场分析

依据PIV测量实验结果，对一个波长范围内类波形壁面湍流边界层流场情况展开讨论，不同振幅波长比的类波形壁面对流场的影响表现出类似特征，统计量云图与曲线基本互相吻合，因此以振幅与波长之比为21/＝0.033的情况为例进行详述．

2.1 4个法向位置的速度与压力分析

应用PIV技术测量了类波形壁面一个波长范围内的流场情况，根据测量结果，绘制了一个波长范围流场中＝0.02、0.11、0.22、0.44共4个法向高度的流向与法向速度分布曲线如图5所示，其中为边界层名义厚度．观察图中一个波长范围内流向、法向速度变化，可以看出类波形壁面与常规小尺度波形壁面流场速度的分布趋势基本一致，壁面对流场的影响主要表现于近壁区域．

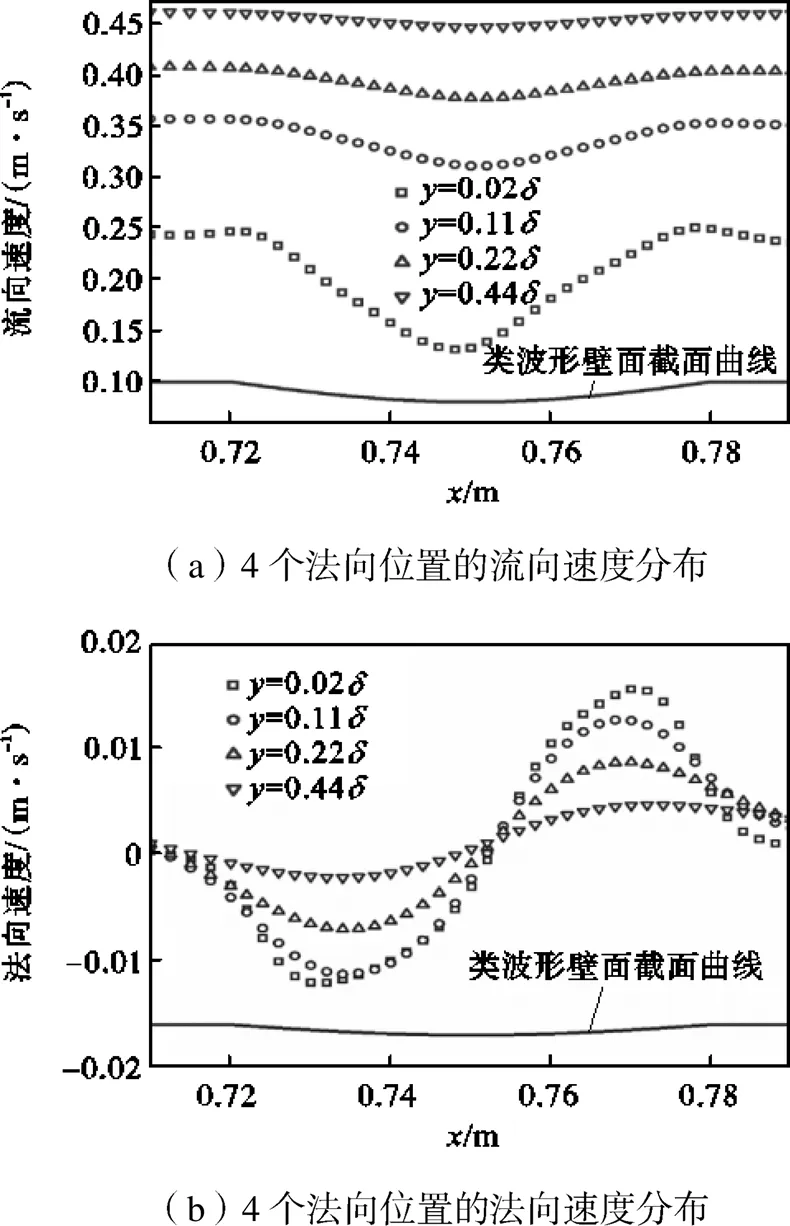
图5 一个波长内速度分布

由图5(a)可知，一个波长范围内流向速度变化与波形起伏同步，在波形结构波峰位置流向速度出现最大值，在波谷位置现最小值，流向速度大小表现出由高到低再到高的振荡分布，越是远离壁面的区域这种趋势越弱；由图5(b)可知，一个波长范围内法向速度变化也与波形起伏同步，处于波形结构下坡阶段的流体法向速度为负值，该范围内法向速度的变化趋势为先下降后升高，在下坡半程附近区域流体的法向速度出现最小值，波形结构内爬坡过程与下坡过程的法向速度的分布基于波谷呈现“中心对称”．

流场中速度的变化通常由压力变化引起，由于PIV测试实验设备无法对流场内压力进行直接测量，应用Fluent软件对模型进行了数值仿真，得到相同边界条件下一个波长内的压力分布仿真结果，如图6所示．仿真结果显示流场中压力变化趋势与流向速度变化趋势相反．压力在“波峰-波谷-波峰”范围内表现出“极小值-极大值-极小值”的变化规律，下坡段区域为逆压梯度，爬坡段区域为顺压梯度．仿真结果与Zilker等[19]对波形壁面一个波长范围内的测量结果显示的压力分布趋势基本吻合．

综合分析一个波长内的压力与速度的变化趋势，可知波形壁面下坡段的逆压梯度使流动减速，波谷处速度出现最小值，爬坡段的顺压梯度则使流动加速，在波峰处速度出现最大值．

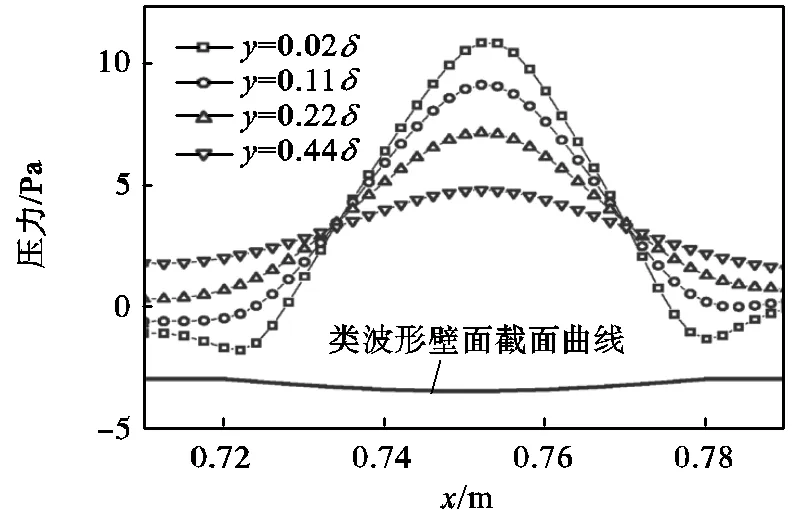
图6 一个波长内压力分布

2.2 5个流向位置的速度曲线

进一步分析压力分布对流速的影响，根据PIV实验测量结果，在类波形壁面流场中的一个波长范围内，绘制5个均匀分布流向位置的流向速度分布及波长平均的速度剖面，如图7所示．

波形壁面形貌的起伏决定了在对不同流向位置的速度剖面进行研究之前，需要定义各流向位置的法向坐标原点．一般将坐标原点选取为波峰与波谷法向坐标的中间点，但由于本研究中的类波形壁面形貌与常规波形壁面存在区别，且相对尺度较大，缺乏对近似原点定义的参考，因此每一个观测点的法向坐标原点均通过实验拍摄图片进行精确确定，使各个流向位置的法向坐标原点位于壁面处．本节中各个观测点的法向坐标原点均以0表示．

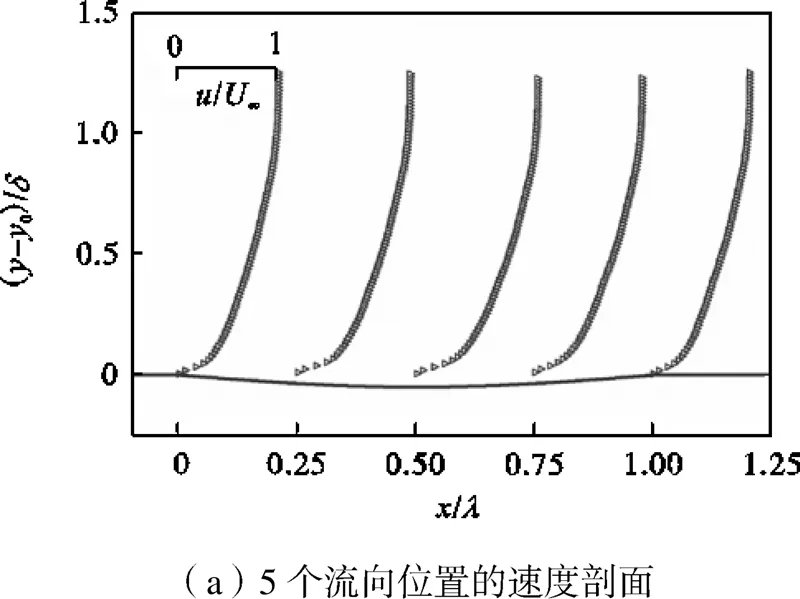
图7(a)给出一个波长内/＝0、0.25、0.50、0.75、1.00这5个流向位置处以来流速度∞无量纲化的平均速度剖面．结合图6，注意到/＝0、0.50、1.00这3个流向位置处压力梯度的符号发生改变，意味着流动的加减速状态剧烈变化，使流动变得不稳定，相应地，在图7(a)中上述3个流向位置处流向速度剖面出现拐点．

图7(b)为图7(a)中5个流向位置的剖面进行波长平均得到的速度剖面，该速度剖面同样符合经典的对数律分布规律．图7(c)对比了5个流向位置的速度剖面与波长平均的速度剖面，在对数律分布的法向坐标下对比发现：一个波长范围内5个流向位置的流向速度剖面在靠近壁面的区域差异最大，随着壁面法向距离的增加这种差别逐渐减弱；在/＝0.25、0.75位置处流向速度剖面基本吻合，且与波长平均速度剖面最为接近，/＝0.50位置的流向速度小于波长平均速度，越靠近壁面速度的差值越大，/＝0、1.00位置处流向速度剖面基本吻合，流向速度均大于波长平均速度，越靠近壁面速度的差值越大．图7总体反映出一个波长范围内流动的周期性变化，各位置流向速度及波长平均的速度分布情况印证了第2.1节中讨论的压力梯度对速度场的影响．在流场中，一个波长范围内减速效果积累最强的位置位于波谷，波谷位置速度出现极小值；加速效果积累最强的位置位于波峰，波峰位置处速度出现极大值，一个波长范围流场中流速介于这两个极值之间．

2.3 速度云图

图8(a)、(b)给出PIV实验拍摄区域的流向、法向速度云图．观察图8(a)可看出波形结构上方近壁湍流边界层厚度增加，波形结构内部存在低速流体；由图8(b)可知流体的法向速度在波形结构上方边界层内表现出特征明显的高、低速区域．结合第2.1节与第2.2节中类波形壁面一个波长范围近壁湍流边界层内流体的流向、法向速度及压力分布规律，可知，当流体流经波形结构时，在其内部汇聚形成低速流体，这些低速流体可以起到类似于润滑剂的作用，高速流体从充当润滑剂的低速流体上方流过，使流体与物体表面之间的液体与固体摩擦转化为液体与液体之间的摩擦[10]．与光滑壁面相比，类波形壁面可显著降低摩擦阻力．

3 统计量分析

根据PIV测量实验结果，对类波形壁面末尾波形单元下游紧邻的平板区域各阶统计量进行分析．

3.1 平均速度剖面

实验测量得到的3种振幅波长比的类波形壁面及零压力梯度光滑壁面的流向平均速度剖面如图9所示，流向平均速度均用壁面摩擦速度u进行无量纲化，给出对数率曲线．根据利用平均速度剖面测量u的方法[20]，基于平板湍流边界层对数区无量纲速度和法向高度满足关系

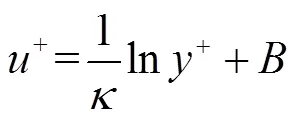
式中B为常数．利用牛顿迭代法和最速下降法拟合获得壁面摩擦速度uτ．

观察图9可知，在48cm/s实验来流速度下光滑壁面近壁湍流边界层内平均速度剖面符合湍流边界层的经典分布[21]，相较之下类波形壁面上流场的平均速度剖面在缓冲层有所提高，对数区出现上移．

表1列出了不同壁面上湍流边界层的基本参数及减阻率．表中边界层名义厚度为湍流边界层中流体速度约为0.99倍来流速度时距离壁面的法向高度，雷诺数Re与边界层厚度和壁面摩擦速度u相关，减阻率DR定义为

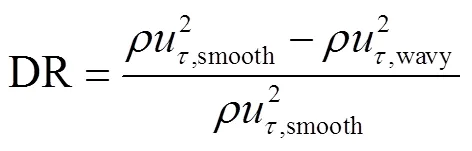
式中：为流体密度；下标wavy代表波形壁面，smooth代表光滑壁面．

表1 湍流边界层基本参数和减阻率

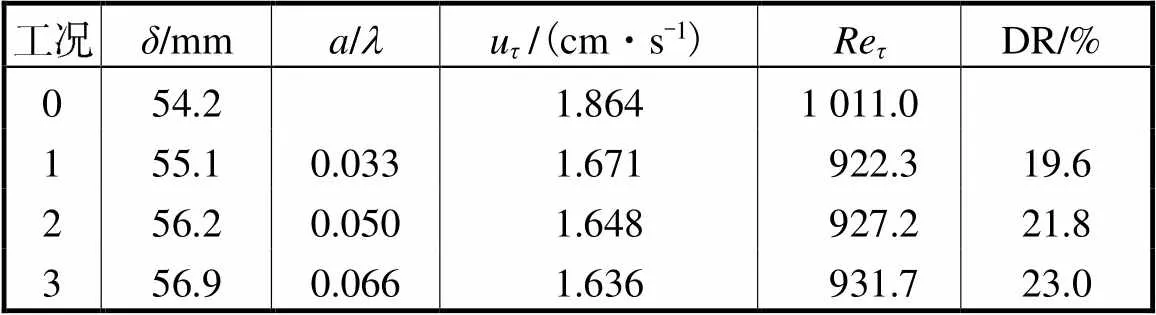
Tab.1　　Turbulent boundary layer basic parameters and drag reduction rate

注：工况0为光滑壁面.

3.2 雷诺应力

雷诺应力是由湍流脉动速度引起动量交换而产生的附加应力．根据PIV测量实验结果，对比了3种振幅波长比的类波形壁面末尾波形单元下游紧邻的光滑平板区域与零压力梯度光滑壁面的雷诺应力分布，见图10，其中-+、-+用进行无量纲化．

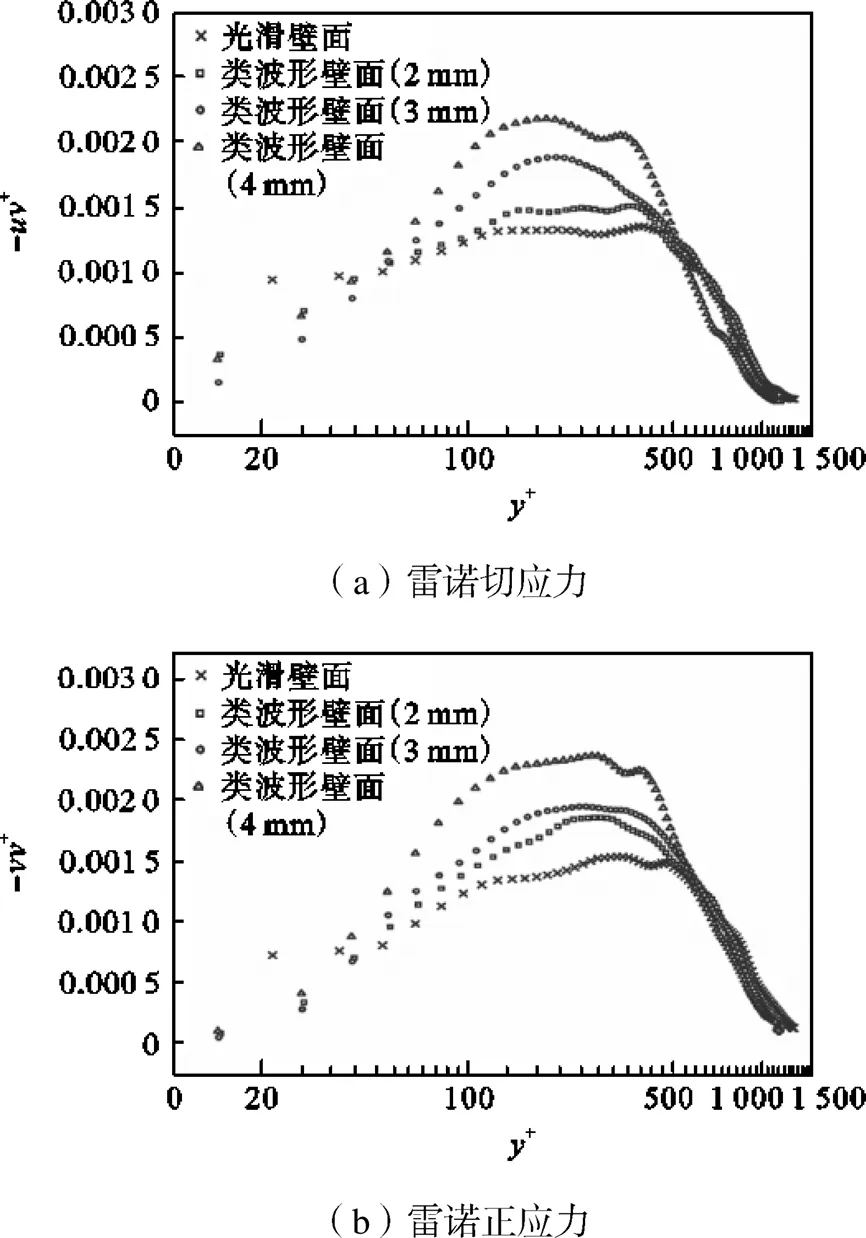
图10 各壁面流场雷诺应力的分布曲线

由图10(a)可知，光滑壁面上方的雷诺切应力曲线在＋≈200的位置出现峰值，对比之下，3种振幅波长比的类波形壁面流场的雷诺切应力曲线峰值均有一定的升高，峰值出现的位置外移，且升高幅值随类波形壁振幅与波长之比的增大而增加；类波形壁面上方的雷诺切应力在＋≤35的黏性区相较于光滑壁面有明显的下降，这一特征延伸至一定范围内的对数区，说明在类波形壁面作用下近壁区流场的动量交换被抬升至远离壁面的区域；＋≈90时类波形壁面上方的雷诺切应力反超光滑壁面，并在90～500的无量纲壁面法向距离范围内出现高雷诺切应力区，类波形壁面的振幅波长比越大，该范围内的雷诺切应力越大，流体的动量交换越剧烈，可知近壁区域的动量交换减弱幅度越大，与表1中类波形壁面减阻率随振幅波长比增加而逐渐增大的规律相互吻合．

图10(b)中，类波形壁面流场的雷诺正应力分布与雷诺切应力分布特征相似，3种振幅波长比的类波形壁面上方近壁区的雷诺正应力均低于光滑壁面.综上所述，类波形壁面湍流边界层近壁区雷诺应力的降低说明湍流中的动量交换被沿法向抬升至远离壁面的区域，湍流脉动最强的位置更加远离壁面，近壁区湍流脉动被抑制，壁面摩擦阻力下降．PIV测量实验结果表明类波形壁面具有良好的减阻效果，减阻率随着振幅波长比的增加逐渐增大，最大减阻率达23.0%．

4 结 论

(1) 根据一个波长范围边界层内4个壁面法向距离处流、法向速度及压力分布的测量及仿真结果可知，类波形壁面与常规小尺度波形壁面对流场的影响类似，结合压力与速度的变化趋势，下坡段附近的逆压梯度使得流动减速，波谷处速度出现最小值，波谷之后的爬坡段附近的顺压梯度则加速了流动波峰出流速出现最大值．

(2) 对比了5个流向位置的流向速度剖面与波长平均的速度剖面，波谷和波峰处的速度剖面印证了压力梯度对速度场的加减速影响．

(3) 对不同振幅波长比的类波形壁面末尾波形单元下游平板区域与零压力体度光滑壁面的各阶统计量的测量进行对比，结果表明：3种振幅波长比类波形壁面的平均速度剖面均具有减阻壁面的典型特征，雷诺应力的峰值相对光滑壁面略有外移，近壁区流场雷诺切应力具有明显的降低，湍流中的动量交换被法向抬升至远离壁面的区域，近壁区湍流脉动被抑制，减阻性能良好，最大减阻率达23.0%．

最后需要指出的是，在本文的雷诺数流场工况下，3种类波形壁面减阻机理相同，效果随着振幅波长比增大而持续增加，同步进行的仿真研究结果表明在流速继续增大直到15m/s的更大流速范围内类波形壁面均具有良好的减阻效果．后续可对类波形壁面波长和振幅参数的进一步优化设计研究，可创造实验条件对更大流速下的类波形壁面开展实验研究成为关键．

［1］ Adrian R J. Hairpin vortex organization in wall turbulence[J]. Physics of Fluids，2007，19：041301.

［2］ Eitel-Amor G，Flores O，Schlatter P. Hairpin vortices in turbulent boundary layers[J]. Journal of Physics： Conference Series，2014，506：012008.

［3］ Lu S S，Willmarth W W. Measurements of the structure of the Reynolds stress in a turbulent boundary layer[J]. Journal of Fluid Mechanics，1973，60(3)：481-511.

［4］ Choi K S. Near-wall structure of a turbulent boundary layer with riblets[J]. Journal of Fluid Mechanics Digital Archive，1989，208：417-458.

［5］ Orlandi P，Jiménez J. On the generation of turbulent wall friction[J]. Physics of Fluids，1994，6(2)：634-641.

［6］ Cook G W. Turbulent Flow over Solid Wavy Surfaces[D]. Urbana-Champaign：University of Illinois at Urbana-Champaign，1970.

［7］ Wagner C，Kuhn S，von Rohr P R. Scalar transport from a point source in flows over wavy walls[J]. Experiments in Fluids，2007，43：261-271.

［8］ Nakagawa S，Hanratty T J. Particle image velocimetry measurements of flow over a wavy wall[J]. Physics of Fluids A，2001，13(11)：3504-3507.

［9］ Hamed A M，Kamdar A，Castillo L，et al. Turbulent boundary layer over 2D and 3D large-scale wavy walls[J]. Physics of Fluids，2015，27(10)：479-504.

［10］ Calhoun R J，Street R L，Koseff J R. Turbulent flow over a wavy surface：Stratified case[J]. Journal of Geophysical Research：Oceans，2001，106(C5)：9295-9310.

［11］ 王 维，姜 楠. 波形壁面湍流相干结构TR-PIV测量和POD分析[C]//第7届全国流体力学学术会议论文摘要集. 桂林，中国，2012：142.

Wang Wei，Jiang Nan. TR-PIV measurement and POD analysis of turbulent coherent structure on wavy wall[C]//Abstracts of the 7th National Conference on Fluid Mechanics. Guilin，China，2012：142(in Chinese).

［12］ 葛铭纬. 波形壁面展向振荡减阻研究[C]//第9届全国流体力学学术会议论文摘要集. 南京，中国，2016：85.

Ge Mingwei. Study on drag reduction of wave wall spanwise oscillation[C]//Abstracts of the 9th National Conference on Fluid Mechanics. Nanjing，China，2016：85(in Chinese).

［13］ Vlachogiannis M，Hanratty T J. Influence of wavy structured surfaces and large scale polymer structures on drag reduction[J]. Experiments in Fluids，2004，36(5) ：685-700.

［14］ Yamagata T，Fujisawa N. Experimental and numerical studies of flow field and mass transfer phenomena on sinusoidal wavy walls[J]. Heat and Mass Transfer，2021，57：715-722.

［15］ Shoemaker P A， Ridgway S H. Cutaneous ridges in odontocete[J]. Marine Mammal Science，1991，7(1)：66-74.

［16］ Wainwright D K，Fish F E，Ingersoll S，et al. How smooth is a dolphin? The ridged skin of odontocetes[J]. Biology Letters，2019，15(7)：20190103.

［17］ Song Xiaowen，Lin Pengzhe，Liu Rui，et al. Skin friction reduction characteristics of variable ovoid non-smooth surfaces[J]. Journal of Zhejiang University-Science A：Applied Physics & Engineering，2017，18(1)：59-66.

［18］ Tang Z Q，Jiang N. Statistical scale of hairpin packets in the later stage of bypass transition induced by cylinder wake[J]. Experiments in Fluids，2012，53(2)：343-351.

［19］ Zilker D P，Cook G W，Hanratty T J. Influence of the amplitude of a solid wavy wall on a turbulent flow. Part 1. Non-separated flows[J]. Journal of Fluid Mechanics，1977，82(1)：29-51.

［20］ 樊 星，姜 楠. 用平均速度剖面法测量壁湍流摩擦阻力[J]. 力学与实践，2005，27(1)：28-30.

Fan Xing，Jiang Nan. Skin friction measurement in turbulent boundary layer by mean velocity profile method[J]. Mechanics in Engineering，2005，27(1)：28-30(in Chinese).

［21］ Schlatter P，Örlü R，Liu Q，et al. Turbulent boundary layers up toRe＝2500 studied through simulation and experiment[J]. Physics of Fluids，2009，21：051702.

TR-PIV Experimental Investigation of Turbulent Boundary Layer over a Large-Scale Wave-Like Wall

Tang Jun1, 2，Yan Yitian1, 2，Liu Yanyan1, 2

(1. School of Civil Engineering，Tianjin University，Tianjin 300350，China；2. Tianjin Key Laboratory of Port and Marine Engineering，Tianjin University，Tianjin 300350，China)

A large-scale wave-like wall was designed to overcome difficult processing and expensive maintenance caused by the small scale of a traditional wavy wall. By enlarging and improving the skin ridge structure of killer whale，the large-scale wave-like wall can be better suitable for engineering practice. The influence of the large-scale wave-like wall on the turbulent boundary layer was studied，and its drag reduction effect and drag reduction mechanism were analyzed. To experimentally measure the turbulent boundary-layer flow fields on smooth walls and three large-scale wave-like walls with the amplitude-to-wavelength ratios of 21/＝0.033，22/＝0.050，and 23/＝0.066，the time-resolved particle image velocimetry(TR-PIV)technique was adopted. After calculating the spatio-temporal correlation functions in the flow field and comparing the flow velocity，normal velocity，and pressure distribution in a wavelength range，it was observed that the difference in the morphological parameters does not affect the existence of pressure gradients within the turbulent boundary layer of the new large-scale wave-like wall；the inverse pressure gradient near the downhill section decelerates the flow，whereas the compliant pressure gradient near the climbing section accelerates the flow，with the strongest deceleration effect at the trough and the strongest acceleration effect at the beginning and end of the trough，and the velocity in the flow field hovers within two extreme values. Comparison of the order statistics in the plate area immediately behind the last spreading notch of the new wave-like wall for different operating conditions shows that the average velocity profile of the three new wave-like wall surfaces in the logarithmic region shows different magnitudes of elevation；and the average velocity of the near-wall area have different degrees of increase. Further，the near-wall area flow field Reynolds shear stress significantly reduced；near-wall area turbulent pulsation is suppressed；peak Reynolds stress is slightly outward relative to the wall surface. Three types of wave-like wall surface have a certain effect on drag reduction，with the maximum drag reduction rate of 23.0%.

wavy wall；turbulence；time-resolved particle image velocimetry(TR-PIV)；Reynolds stress；resistance reduction；bionic

10.11784/tdxbz202108052

O357.52；O357.54

A

0493-2137(2023)03-0267-08

2021-08-21；

2021-12-23.

唐 俊（1979—  ），男，博士，副教授.

唐 俊，tangjun@tju.edu.cn.

国家自然科学基金资助项目(11204010).

Supported by the National Natural Science Foundation of China(No. 11204010).

(责任编辑：樊素英)