“天问一号”火星探测器着陆控制方案研究

阮吉利，李洪轩，邱科悦，郝立丽

（东北林业大学，黑龙江 哈尔滨 150040）

“天问一号”火星探测器于2021年5月中旬在火星乌托邦平原上顺利着陆，我国首次火星探测任务取得了巨大的成功。在此之后，“祝融号”火星车将对着陆点依次执行全球成像、自我检查、脱离着陆平台和巡逻检测等工作[1]。“天问一号”的成功着陆，是我国航天事业特别是行星探测领域发展的又一个里程碑，同时也表明我国成为世界上第二个着陆火星的国家。本文收集关于火星探测器的信息资料，就“天问一号”的着陆过程建立模型，基于时间最短、能耗最少的原则，对操控方案进行设计，并结合实际情况对操控方案进行检验。

1 “天问一号”着陆过程耗时最短控制策略分析

1.1 “天问一号”落火过程分析

搜集相关信息后，本文将“天问一号”着陆过程简化为以下5个阶段。

第一阶段：两器分离段。探测器于火星停泊轨道上运动，寻觅到合适的着陆时机后通过发动机点火减速降轨。降低到一定高度后，探测器分离为环绕器与着陆器，着陆器向火星坠落；环绕器则在分离半小时后点火加速升轨，返回停泊轨道。

第二阶段：气动减速段。着陆器进入火星大气后，受到空气阻力的影响，速度大幅减小。

第三阶段：伞系减速段。着陆器打开降落伞，由于降落伞与空气的接触面积较大，空气阻力大，能有效减小着陆器的速度。

第四阶段：动力减速段。探测器通过发动机点火的方式进一步减小了速度。

第五阶段：悬停避障与缓速下降段。在高度降为100 m时，探测器的速度基本降到0。探测器悬停避障，寻找最安全的着陆地点，最后通过4个着陆腿的缓冲作用在火星表面软着陆。

1.2 模型建立

为设计控制方案使得着陆的时间最短，主要控制3个环节：环绕器与着陆器分离；打开阻尼伞的时机；发动机点火的时机。3个环节息息相关，必须综合决策。查阅资料可得：近火点高度Hc=280 km；远火点高度Hf=59 000 km；火星平均半径R=3 397 km；轨道为椭圆。决定着陆前，探测器将环绕火星运动。

1.2.1 环绕器与着陆器的两器分离段

设探测器在距离火星h1时进行减速降轨，根据近火点高度Hc和远火点高度Hf可得280 km＜h1＜59 000 km。探测器在发现合适的着陆时间后，通过发动机喷气减速。为了简化问题的分析，假设这一减速过程所需时间可忽略不计。

根据万有引力定律F万=mg，火星重力加速度为其中m为“天问一号”在各个阶段的质量；M为火星质量；G为引力常量。但由于探测器距离火星的高度相对于火星半径不可忽略，则探测器在距离火星h1处的火星重力加速度为

为方便计算，本文取g″为降轨时探测器所处高度重力加速度与到达火星大气时重力加速度的平均值，即

式中：h2为火星大气层距离火星地面的高度。

探测器沿着切线方向具有初速度，且该速度小于火星的第一宇宙速度。而在靠近的过程中，探测器将分离为环绕器与着陆器，环绕器通过加速升轨，不影响着陆器的运动。综上，可将探测器进入火星大气前的运动视为平抛运动。

根据动能与势能的转换公式，动能为

式中：v0为垂直火星方向上探测器的速度；h=h1-h2。从而推出着陆器进入火星大气时，探测器在竖直方向的速度为

探测器降轨到进入火星大气耗时t0为

1.2.2 气动减速段和伞系减速段

进入火星大气后，“天问一号”主要受重力和空气阻力。着陆器进入火星大气后，高度对重力加速度的影响可以忽略不计，因此，取重力加速度g=3.71 m/s2；着陆器所受重力即为G1=mg。

设着陆器进入火星大气后，经过时间t1打开阻尼伞，伞降时间t2后进入动力减速段。为得到着陆器在气动减速段、伞系减速段中，其位移与时间的关系，本文做了如下尝试。下面为便于公式的书写，令则空气阻力F=kv2。

在气动减速段，着陆器在下落过程中只受到重力和空气阻力的作用，且重力的方向与空气阻力的方向相反。由牛顿第二定律mg-kv2=ma，可得出

通过一定的转化，可将该方程式（6）转化为黎卡提方程[2]，从而解得

由于着陆器长、宽各约4 m，底盘是圆形[3]，因此迎风面积S1约为12.56 m2；火星大气的空气密度ρ为0.015 8 kg/m3[4]；空气阻力系数C为1.5。因此，上文设定的

在气动减速段，着陆器进入火星时的初速度即为两器分离段的末速度。

经过时间t1后，着陆器的速度为

着陆器的运动路程为

与气动减速段类似，在伞系减速段，着陆器同样做变加速运动，主要区别在于伞系减速段中着陆器展开的降落伞增加了着陆器与空气的接触面积，故k值发生了改变。此时，降落伞面积S2为300 m2，ρ与C保持不变，计算得

同理，这一阶段（伞系减速段）的初速度为上一阶段（气动减速段）的末速度，经过时间t2后，着陆器的速度为

着陆器的运动路程为

1.2.3 动力减速段

考虑到“天问一号”在动力减速段已经接近火星表面，且速度比前几个阶段较低，因此该阶段忽略火星大气阻力对着陆器的影响[5]。

在动力减速段，着陆器扔掉大底和背罩，发动机点火向地面喷气，通过反推力减速，着陆器共有27台发动机，包括20台250 N、6台25 N和1台7 500 N的发动机。故着陆器的最大推力为12 650 N。

达到动力减速段时，着陆器的速度为v2，其在最大推力的情况下加速度为

由于动力减速段着陆器为了悬停，末速度必须为0，因此动力减速段所用时间着陆器在动力减速段经过的位移x3为

1.3 模型求解

该模型得到的方程组约束条件是决策变量的非线性表达式，故利用MATLAB软件编程，先使用蒙特卡罗模型获得决策变量的初始值，再使用非线性规划模型进行最优化求解[6]。目标函数为

其约束条件为

式中：h=h1-h2，火星半径R=3 397 km；火星上的重力加速度g=3.71 m/s2；k1=0.149；k2=2.830；探测器与火星的距离h1为自变量；火星大气层高度h2=125km。不考虑燃料质量，着陆器质量m=1 285 kg，模型求解步骤如下。

1）通过蒙特卡罗模型模拟，在给定决策变量范围内生成1亿组随机数，从实验点中找到可行点。

2）通过“打擂台”思想，从可行点中找出最小可行点x0，得h1=5 967.365 km；t1=285.77 s；t2=74.68 s；t3=67.43 s。

3）再将得到的x0代入非线性规划模型，分别通过内点法、序列二次规划法、有效集法和信赖域反射算法4种算法，搜索寻求最优的决策变量。

4）通过比较4种算法获得的最优决策变量，选取更优解。

5）最终选取内点法获得的决策变量。得到h1=6 135.637 km；t0=2 505.3 s；t1=263.67 s；t2=73.23 s；t3=64.65 s；z=2 906.85 s。即“天问一号”着陆过程的最短总时长z为2 906.85 s。

2 “天问一号”着陆过程耗能最少控制策略分析

2.1 模型建立

该处主要探讨在给定的着陆时间下，着陆器耗能最少的方案，故假定着陆器从降轨到进入大气的持续时间t0、气动减速段持续时间t1、伞系减速段持续时间t2均为已知量。

通过对探测器着陆各个阶段的研究，本文认为能量消耗的主要阶段为降轨减速段以及进入火星大气后的动力减速段。

2.1.1 探测器降轨减速段

当探测器在火星停泊寻找到合适的着陆时机后，发动机将点火制动，减小速度以实现降轨。在该阶段中，发动机点火消耗的能量等价于探测器动能的变化量。

根据动能定理，该阶段着陆器消耗的能量为

为使能量消耗最少，vt应该尽量大；但同时vt又应该小于火星的第一宇宙速度，否则着陆器将无法坠向火星，故取

依据着陆器从降轨到进入大气的持续时间t0，可知探测器降轨时的停泊轨道距离火星大气的高度由此可得探测器距离火星的距离h1=h0+h2=h0+125 m。

由开普勒定律，任何椭圆天体轨道的中心天体一定在椭圆的一个焦点上。同时根据椭圆的定义b2=a2-c2，得出方程组为

联系万有引力定律与牛顿第二定律，可以列出“天问一号”在近火点和远火点的运动学方程组为

式中：vc和vf分别为着陆器在近火点的速度和在远火点的速度；ρc与ρf分别为近火点和远火点的曲率半径，联立以上各式，代入参数，得近火点速度vc=4.691 5×103m/s，远火点速度vf=890.538 2 m/s。

根据开普勒第二定律可得

根据能量守恒定律可得

由此得着陆器在火星海拔h1上的速度v0为

2.1.2 动力减速段

着陆器在进入大气后将先后经过气动减速段、伞系减速段以及动力减速段。

根据伞系减速段的运动规律，着陆器受到的空气阻力与其运动方向相反，且该阻力的值与速度的平方成正比。因此，起初着陆器受到的空气阻力大于其重力，着陆器做减速运动。而空气阻力的值随着速度的减小而减小，直到与重力达成平衡，着陆器将近似做匀速运动[7]。由于t0、t1为已知量，因此根据式（8）可以算出着陆器做匀速运动时的速度，不妨令其为v。

在伞系减速到某一高度后，着陆器将通过发动机点火来实现减速。假设着陆器在距离火星地面高度为h3时开始进行动力减速，此时速度为v，为了进行后续的悬停避障，在距离地面高度为100 m时着陆器速度应减小为0。根据能量守恒定律，在动力减速段中，发动机所做的功为

设发动机推力为F推（0 N＜F推＜12 650 N）。动力减速段，竖直方向上着陆器受重力以及发动机推力。因此，着陆器在动力减速段做匀减速运动，加速度为

为满足着陆器距离地面100 m时悬停的条件，可得

2.2 模型求解

2.2.1 降轨减速段求解

在探测器的降轨减速段，本文通过开普勒定律、牛顿第二定律等对探测器在火星停泊轨道上的运动做了分析，在着陆器从降轨到进入大气的时间已知的前提下，推导出了探测器降轨时的速度。并在基于能量消耗最小化的考量下，得到了探测器降轨前后的速度，从而利用动能定理得到了降轨减速段的能量消耗。

整理相关公式可得方程组为

此处取t0为1 000 s，解得v0=4.396 3×103m/s；E1=1.678 2×107kJ。

2.2.2 动力减速段求解

有关动力减速段所描述的问题，可由一个有约束条件的线性规划问题解释。因此，本文用遗传算法对本问题的模型进行求解[8-9]。

目标函数为

其约束条件为

模型求解步骤如下。

1）将决策变量排列为1个个体，初始种群由2 000个随机产生的个体组成。

2）编写适应函数，来计算个体的性能指标。

3）选择出指标较好的个体留存，并遗传给下一代。

4）随机将个体两两配对，并按照规定的交叉概率进行交叉。

5）若最大进化代数达到了20 000，则进行最优解的输出；否则继续进行编码、评价、选择、交叉等操作。

通过约束条件的分析，本问题的模型确定了交叉概率为0.6。对模型进行求解，得到v取90 m/s时，h的最优解为660.21 m。此时，由于E2=8 351.702 kJ，因此E=E1+E2=1.679×107kJ。

3 “天问一号”着陆模型与实际情况的匹配度检验

探测器的着陆数据如下。

1）两器分离段结束，着陆器飞行3 h后进入火星大气（火星大气层高度为125 km）。

2）气动减速段：着陆器在约290 s内，将速度从4.8 km/s减速到460 m/s。

3）伞系减速段：在距离火星地面11 km左右处，探测器打开降落伞，在约90 s内将速度由460 m/s降至95 m/s。

4）动力减速段：距离火星地面1.5 km左右处，探测器通过发动机进一步减速，用80 s左右的时间将速度减小到3.6 m/s。

5）着陆缓冲段：在距离火星表面约100 m时，着陆器的速度基本降为0。

前文对着陆器的着陆过程建立了运动模型。为验证与评估该模型的科学性，本文代入3个参数值：进入火星大气时的速度（4 800 m/s）、气动减速段持续的时间（290 s）、伞系减速段持续的时间（90 s），则用于求解的方程组为

解得气动减速段的位移为103.120 1 km，伞系减速段的位移为11.642 2 km，动力减速段的位移为1.337 7 km。对比“天问一号”着陆时在这3个阶段的实际位移114 km、9.5 km、1.5 km，利用公式求得相对误差分别为9.54%、22.6%、10.82%。其中，Er为相对误差；T为真实值。由此可知，本文建立的模型与实际的着陆过程存在可忽略不计的误差。

随后，本文取10组着陆器进入火星大气时速度与气动减速段持续时间的数据，代入模型运算，得到气动减速段的位移，对取得的数据拟合后，得到计算值与真实值的拟合图（见图1）。

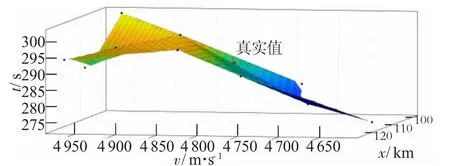
图1 计算值与真实值的拟合图

由图1可知，真实值与拟合所得曲面的计算值较为接近。综上，可认为本文对于着陆过程所建立的运动模型与实际情况较相符，准确度较高。

4 结论

本文通过数学和物理方法，对“天问一号”探测器着陆的各个过程进行分析，建立运动模型方程。首先，以着陆时间最短为优化目标，明确自变量、约束条件后，建立了单目标优化模型，用非线性规划模型进行最优化求解，解得着陆的最短总时长为2 906.85 s。其次，在给定着陆时间的前提下，建立以能量消耗最小为目标，以发动机推力、点火时间为自变量，以着陆器在火星海拔100 m时速度为0为约束条件的优化模型，并利用遗传算法进行了规划求解，解得在确立各个阶段用时的前提下，着陆最少消耗能量为1.678 2×107kJ。最后，为检验运动模型的准确性，本文搜集了“天问一号”着陆的真实值数据，代入模型计算后发现误差较小，具有一定可信性。