教学质量评价中的AHP群推理模型应用研究*

余新桥

(四川工商职业技术学院智能制造与信息工程学院，四川 成都 611830)

课堂教学质量评价是高校教学质量的重要组成，是衡量高校教学水平的重要指标[1]。通常采用的教学评价指标有：课前教学准备、搞好教学组织、把握好教学内容、采取有效教学方法、恰当进行思政教育等。评价指标体现了教师对多媒体技术的运用、师生互动、授课过程中的课堂气氛、教师备课环节、授课环节、教学目标是否明确等各个方面的效果[2]。评价专家（例如教学督导）对教师在各指标上的授课效果的公正评价，能够极大地鼓励教师发扬自己的优点，督促教师改进自己的不足。常用的评价模型有Delphi法、Topsis法、层次分析法（Analytic Hierarchy Process，AHP）等[3-4]。作为一个较主观的群决策过程，每次教学评价活动都要耗费多位专家的人力和时间，历史的评价过程没有积累成宝贵的经验。鉴于AHP中两两比较评价数据包含的优劣信息和两两比较矩阵的可扩展性，本文提出基于AHP的群推理模型，将历史AHP产生的教学质量评价数据作为案例存储，并作为知识，为新的教学评价活动服务，既能够实现敏捷评价，又不失群决策集思广益的优势。该模型可作为传统的基于过程的教学质量评价活动的有效补充。

后续章节组织如下：第1节介绍相关的理论知识；第2节详细描述提出的AHP群推理模型的工作流程；第3节演示提出的模型在教学质量评价中的应用；第4节总结本文的工作。

1 相关知识

1.1 层次分析法

层次分析法（AHP）由著名管理科学与工程专家Saaty提出，被广泛应用于方案的评价和选择等决策活动中。采用层次分析法进行评价时，决策者通过方案的两两比较给出相对评价值，然后通过计算相对值矩阵的最大特征值对应的特征向量的方法得到每个方案的权重[4]。AHP的形式化描述如定义1所示。

定义1[4]：对于n个待评价方案{x1，…，xn}，决策者首先对方案进行两两比较分析后，给出相对评价值矩阵(apq）n×n，其中apq表示决策者认为方案xp优于或者劣于方案xq的程度；apq满足apq·aqp=1，即(apq）n×n满足互反性；然后计算矩阵(apq）n×n最大特征值对应的特征向量，即方案最终的权重向量为[w1…wn]。

1.2 AHP群决策

定性问题可能会产生较大的主观误差，因此AHP往往结合群体决策法，如定义2所示[5]。

定义2：E={e1，e2，…，eK}表示K个决策专家，那么任一个专家ek的相对评价值矩阵为（akpq）nn，其中p，q=1，…，n；k=1，…，K。针对某个因素或准则，多个专家可将自己的相对评价值矩阵通过定义1得到绝对权重后，再集结成群体评价值。

针对K个值y1，…，yK，常用集结算子为有序加权平均算子（OWA）[6]

式（1）中，y1，…，yK满足其中

2 AHP群推理模型

由于AHP群决策面向过程的特点，历史的教学质量评价过程都无法作为知识保留下来，为以后的复用做准备。为了满足现代教学信息化发展的要求，追求省人力、增效率的目标，教学质量评价活动的传统过程也要向智能、快速的方向发展。

根据Saaty的理论[4]：对于权值{w1，…，wn}，可以构造理想两两比较矩阵最大特征值为n，对应的特征向量为[w1…wn]。如果增加新权值wn+1，理想两两比较矩阵应是最大特征值为n+1，对应的特征向量为[w1…wnwn+1]。

很显然，两两比较矩阵扩展后，原有特征向量的信息可以保留下来。因此在AHP中，对于已有的n个方案{x1，…，xn}的两两比较矩阵（apq）n×n，新增加1个方案xn+1后，对应的两两比较矩阵（apq）（n+1）×（n+1）的最大特征值对应的特征向量虽然受到了矩阵的扩展部分[a（n+1）1a（n+1）2…a（n+1）（n+1）]的干扰，但是仍然保留原来特征向量的信息。另外群决策中的集结算子可以减少单个AHP中的噪音干扰。

基于以上分析，AHP群推理过程描述如下。

输入：历史AHP群决策中以产生的n个教师在每个指标上的两两比较数值矩阵（akpq）nn，其中k=1，…，K。新的待评价的教师xn+1以及评价人将历史待评价教师集{x1，…，xn}对xn+1的两两比较术语L1（n+1），L2（n+1），…，Ln（n+1）。输出：推理新的待评价教师的优先序xP（1），…，xP（n），xP（n+1），其中P（1），…，P（n），P（n+1）为1，…，n，n+1的重排列。

步骤1：将术语L1（n+1），L2（n+1），…，Ln（n+1）通过Saaty（akpq）nn标度转换为互反数值a1（n+1），a2（n+1），…，an（n+1）。

步骤2：让[a1（n+1）a2（n+1）…an（n+1）]成为新的列，[1/a1（n+1）1/a2（n+1）…1/an（n+1）]T成为（akpq）nn新的行，从而将（apkq）nn扩展成（akpq）（n+1）（n+1）。

步骤3：针对每一个指标Co，采用最大特征值法求矩阵（akpq）（n+1）（n+1）的最大特征值对应的特征向量[wk…wkwk]，得到专家e对每个教师在C上o1ono（n+1）ko的效用。

步骤4：针对任一指标Co，通过集结算子f（·）集结专家ek（k=1，…，K）的群体效用[wo1…wonwo（n+1）]，参照式（1）。

步骤5：针对每一个教师，采用集结算子f（·）计算教师的多指标综合效用值W1，…，Wn，Wn+1，参照式（1）。

以上AHP群推理过程见图1。

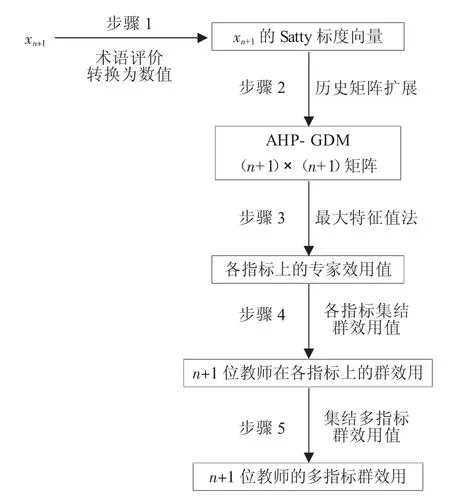
图1 AHP群推理模型

根据W1，…，Wn，Wn+1值的大小，即可得到教师xn+1的排序位置。

3 案例演示

针对笔者所在院校理实一体化课程的3个评价指标（C1，C2，C3），3位专家（e1，e2，e3）分别对3位教师（x1，x2，x3）课堂教学已存在的历史两两比较的AHP矩阵见表1、表2及第14页表3。

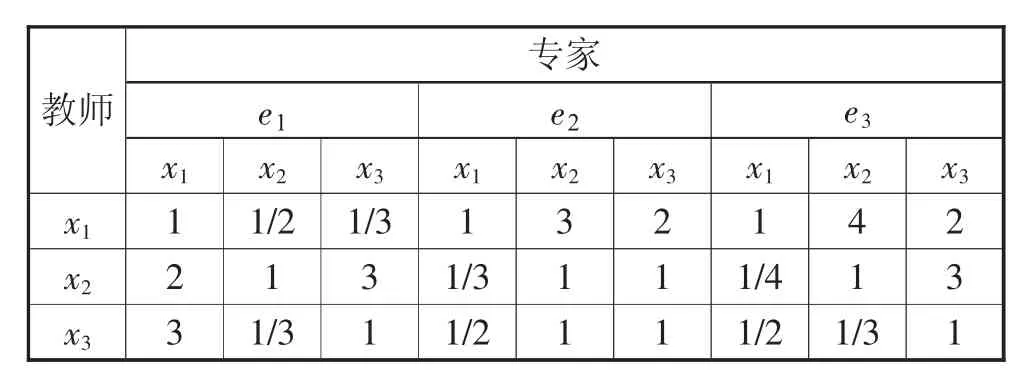
表1 课前教学准备的历史两两比较AHP矩阵（C1）

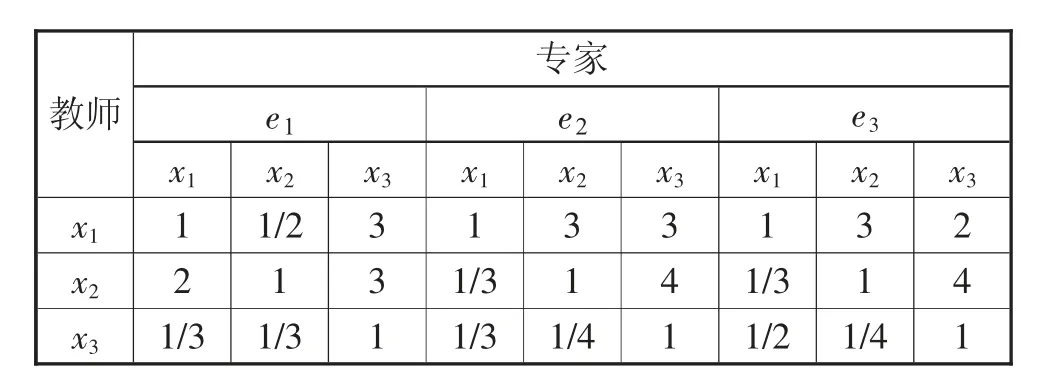
表2 把握好教学内容的历史两两比较AHP矩阵（C2）

术语等级设为7级：L0，L1，…，L6，分别表示很差、差、较差、差不多、较好、好、很好。设新增的评价教师x4，设当前专家将历史教师方案{x1，x2，x3}对x4的比较评价在指标C1，C2，C3上分 别 为{L1，L0，L5}，{L0，L1，L5}，{L1，L4，L5}。根据上述AHP群推理过程，将表1—表3作为历史知识进行复用：根据步骤1和步骤2将新增评价扩展到历史评价矩阵中，再根据步骤3得到各专家在各个指标上的权重值，并根据步骤4得到群体权重值，参照式（1）。

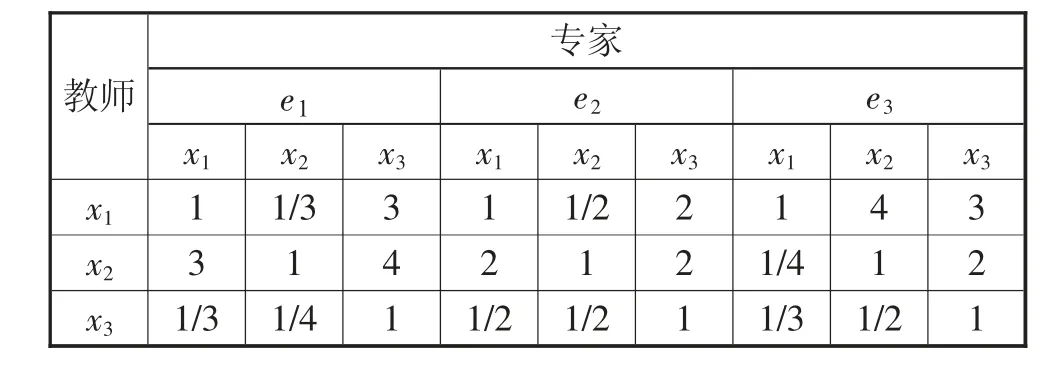
表3 恰当进行思政教育的历史两两比较AHP矩阵（C3）

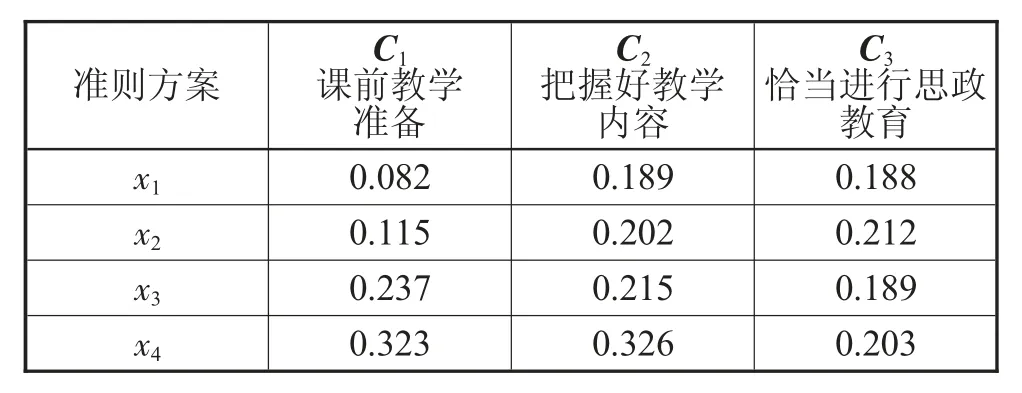
表4 扩展后各个因素准则上的群体权重值

根据步骤5计算教师的多指标综合效用值W1=0.082，W2=0.115，W3=0.189，W4=0.203。最后进行优先级排序，即x4，x3，x2，x1。

4 结束语

教学质量评价是促进教学质量提高的重要手段。为了提高评价的效率，本文提出了一种AHP群推理模型，将历史过程作为知识复用。本方法是传统教学评价活动的有益补充，也符合现代高校教育的信息化需求和发展。