一种斜拉桥拉索倾角修正及主要参数计算方法

郭胤昶

（苏州市太仓市公路事业发展中心，江苏 苏州 215400）

1 引言

斜拉桥是一种桥面体系受压，支撑体系受拉的桥梁[1]。它一般由主梁、索塔和斜拉索三大部分组成。斜拉索作为支撑体系，为主梁提供类似于“弹性支撑”的作用，从而降低主梁弯矩，提高跨越能力。

自20世纪90年代以来，伴随着结构分析理论的进步、高强材料和施工方法以及防腐技术的发展，现代斜拉桥在全世界范围内的应用得到迅速发展。与一般的梁式桥不同，斜拉桥属高次、柔性超静定结构，其设计计算理论较为繁复，通常先进行整体静力计算，经过反复调整成桥索力，以使主梁与塔的内力达到某种目标下的最优或较优状态，同时控制主梁成桥线形满足设计要求，再根据对应的成桥索力对斜拉索主要特征参数进行设计计算。

斜拉索在轴向拉力和自重的作用下，在空中实际呈现为一悬链线而非视觉感官上的直线。为保证拉索在套管出口处居中以便安装减震圈、同时使拉索锚具与锚垫板垂直以使拉索钢丝受力均匀，必须对梁端和塔端的拉索倾角进行修正（尤其针对长索）。否则，拉索钢丝可能与导管内壁碰撞摩擦，无法安装减震器，甚至使得斜拉索钢丝保护层遭破坏而缩短其寿命、严重影响结构受力与安全[2]。

当前，绝大部分常规塔型的斜拉桥出于挂篮施工时通航净空受限及施工便捷性等因素考虑，通常都采用在塔端张拉斜拉索。但随着经济的发展，人们对审美要求不断提高，一些在城市内的市政斜拉桥有特殊的景观要求，其塔的造型一般较为独特、异形，给塔上斜拉索张拉带来较大困难，故此种情况下只能选择梁端张拉方式。本文笔者试图从斜拉索受力状态出发，分析给出一种梁端斜拉索索力控制值下斜拉索倾角修正及其余主要特征参数的简化计算方法，以供同类型桥梁设计参考。

2 斜拉索受力状态及特征参数计算分析

要对斜拉索两端倾角进行修正，实际就是根据斜拉索给定的梁端、塔端坐标，在拉索自重和指定的成桥索力下进行计算，得出拉索的水平倾角。如图1所示，设A 点为斜拉索梁端锚固中心，B 点为塔端锚固中心，以A 点为原点O（即A 与O 重合），桥梁纵向为x 轴，竖向向上为y 轴，建立坐标系，为斜拉索悬链线。

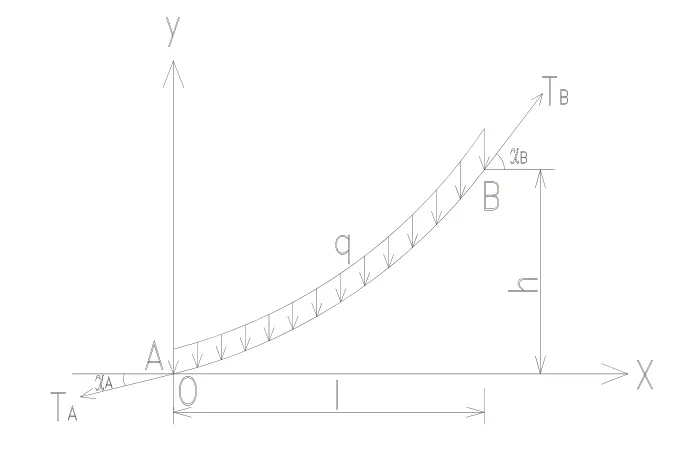
图1 斜拉索受力状态示意图

为推导拉索线形方程，需要先做一些基本假设：①索是完全柔性的，既不能受弯也不能受压，索的截面积与其长度相比十分微小，其截面抗弯刚度在计算时可忽略；②拉索除受到轴向张拉力以外，仅承受自重作用；③拉索材料符合胡克定律，应力与应变满足线性关系。

其中：TA—拉索梁端张拉力；TB—拉索塔端张拉力；q—拉索自重集度；αA—拉索梁端水平倾角；αB—拉索塔端水平倾角；l—拉索纵向水平投影长度；h—拉索塔端锚固点竖向高度。

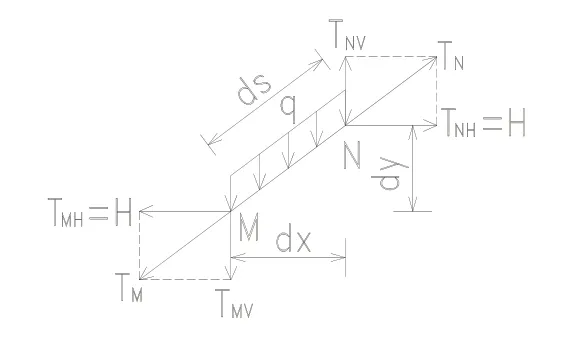
图2 斜拉索微元段受力状态示意图

其中：ds—微元段长度；TM—M 端张拉力；TN—N端张拉力；TMH—M 端张拉力水平分力；TMV—M 端张拉力竖向分力；TNH—N 端张拉力水平分力；TNV—N 端张拉力竖向分力；H—拉索水平分力（先假定为已知）；

又Σx=0，可得：TMH=TNH=H，即拉索水平张力沿全长为定值；

TMV=H·；由微分知识，

其中C1、C2 为待定常数，联立（4）（5）（6）式，可解得：

至此，拉索线性方程解析式确定。设拉索上任一点与水平线夹角为α，则有：

设斜拉索材料弹性模量为E，拉索截面积为A，无应力长度为Su，弹性伸长量为ΔS，有应力长度S 下的理论弹性伸长量为m，拉索张力为T，则：

由相似原理[3]，（7），又ΔS=S－Su （8）

至此，关于斜拉索的几个主要设计参数：拉索任意点水平修正倾角α、拉索弹性伸长量ΔS 及拉索无应力长度Su 等均已确定，但上述公式推导是基于拉索水平分力H 已知的前提下的，实际上H 与修正倾角α 相关，在拉索张力T 已知的情况下，H=T·cosα。理论上在x 值确定的情况下，可以将H=T·cosα 代入上述α的表达式，建立关于α 的三角函数方程式，求出α 的精确解析式，但此过程极其繁杂困难，给实际应用带来很大的不便。鉴于此，笔者采用迭代试算法进行简化计算，本文试图给出梁端（即x=0 时）拉索张拉力TA已知情况下的拉索修正倾角等参数，其思路为：

（1）第一轮先取梁端拉索斜率KA(1)=，则：H(1)=，代入上述C1 表达式求得C1(1)，将C1(1)代入（4）求得公式计算值KA(1)＇；

（2）第二轮取KA(2)=KA(1)’，则：H(2)=，按照同样步骤代入求得C2(2)及KA(2)＇；

（3）第三轮取KA(3)=KA(2)＇…重复以上步骤，KA(n)＇逐渐逼近正确解，当KA(n)＇与KA(n)的误差精度小于人为设定的值（比如2.0e-4，读者可视具体情况自行设定）时，可认为已收敛，此时的H(n)即可认为是要求的水平分力值。

根据笔者大量的实践，直接运用Office Excel 软件，大多数情况下只要经过2 到3 轮的迭代试算，KA误差精度即可达到2.0e-4 以内而收敛，较为方便实用。

3 工程算例

本工程位于某城市主干道上，是一座跨径组合为95+170m 的景观独塔斜拉桥，混合梁+混合塔结构。边跨梁采用搭设满堂支架现浇的预应力混凝土箱梁结构，主跨梁采用悬拼的预制钢箱梁结构，主塔下部采用钢筋混凝土结构，上部采用预制钢箱结构。全桥共设置15对斜拉索，由于桥梁索塔在纵向呈Y 形、横向呈“人”字形，造型较为独特异形，在塔上不便张拉斜拉索，故考虑在梁端张拉，设计给出梁端成桥恒载索力控制值。如图3所示。

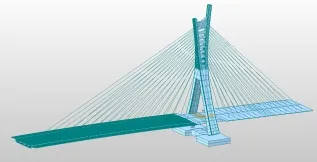
图3 斜拉桥Midas Civil 有限元计算模型

限于篇幅，本文只举主跨5 根斜拉索Z11～Z15（索编号规则为依次远离索塔，下同）说明问题。

表1 斜拉索水平力H 试算表

由上述表格1 计算可看到，经过2 轮迭代，KA误差精度已达到2.0e-4 以内，可以认为已收敛，此时H(2)的值即为所求的水平分力H。拉索梁端及塔端在空间三个投影平面内的修正倾角及空间坐标系示意图如图4所示。

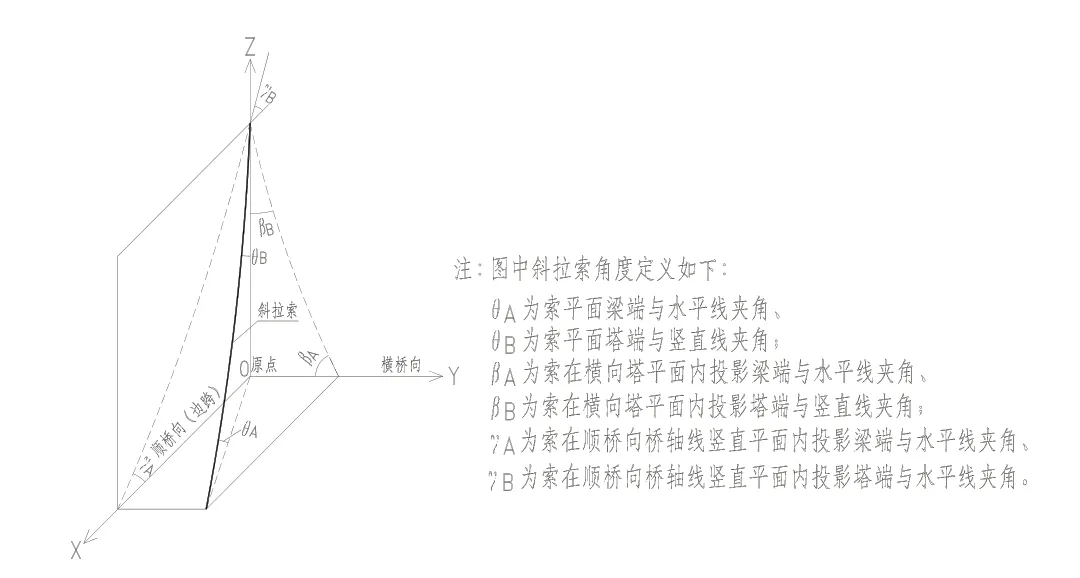
图4 斜拉索空间坐标系及角度示意图

至此，在拉索梁端成桥恒载张拉力控制值TA给定的情况下，拉索梁端及塔端在空间三个投影平面内的修正倾角、弹性伸长量及无应力长度等主要参数均可在Office Excel 表格中完成，如下表2（限于篇幅，本文只给出Z11～Z15 斜拉索主要计算参数）

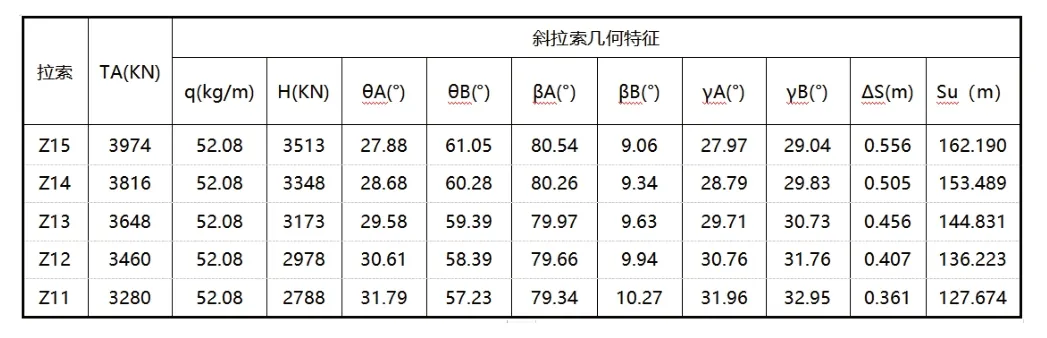
表2 斜拉索主要参数计算表

4 结语

本文结合一些景观斜拉桥的设计、施工实际过程，即只能在梁端张拉斜拉索的工况下，通过符合实际的假设，建立合适的斜拉索空间坐标体系，取斜拉索微元段分析，建立微分方程，进而推导出斜拉索的空间线形解析式，从而给出了梁端成桥恒载索力确定的情况下斜拉索的水平修正倾角、弹性伸长量及无应力长度等主要计算参数的解析式。在此过程中，对于关键的拉索水平分力H 的计算采用迭代式算法，此法具有操作简便、收敛速度快的特点，可供同类型斜拉桥设计人员参考。

另外，本法推导过程具有通用性，若需要在塔端张拉斜拉索，即给定塔端斜拉索成桥恒载索力时，只需在建立坐标系时把塔端斜拉索锚固中心作为原点O，建立类似的微分方程并求出拉索空间线形解析式，得出的拉索各特征参数计算值与上述推导结果均一致，读者若有兴趣可以自行尝试，笔者在此不再赘述。