Engineering topological state transfer in four-period Su-Schrieffer-Heeger chain
2023-03-13XiXiBao包茜茜GangFengGuo郭刚峰andLeiTan谭磊
Xi-Xi Bao(包茜茜) Gang-Feng Guo(郭刚峰) and Lei Tan(谭磊)
1Lanzhou Center for Theoretical Physics,Key Laboratory of Theoretical Physics of Gansu Province,Lanzhou University,Lanzhou 730000,China
2Key Laboratory for Magnetism and Magnetic Materials of the Ministry of Education,Lanzhou University,Lanzhou 730000,China
Keywords: topological state transfer,robust,high fidelity
1.Introduction
Large-scale quantum information processing has drawn a great deal of attention in recent years.[1-16]Undoubtedly, the core concept to achieve quantum information transmission between distant nodes is the robust quantum state transfer.[17-21]Various systems have been explored to realize this process,for example, cavity electromechanical systems,[22-24]spin chain and spin-wave engineering,[5,6,18,21,25]and quantum dots.[26,27]However,one can find that the imperfect(disorder,defect and impurities) of the usual devices and the environment noise inevitably have a negative influence on the fidelity of quantum state transfer.
The role of topology in the field of physics has been studied in many fashions.[28-33]To date,we know that the typical feature of the topological insulators is the existence of the robust edge state protected by the energy gap,[34-38]which provides global protection with respect to the local deformations of the system.[39-43]The invariance under continuous deformations endows the topological insulators with boundless potential applications in quantum information processing and engineering.Correspondingly,there has been a significant surge of interest in investigating robust quantum state transfer using the topological system.[9,12,15,28,44-47]In Ref.[28], Dlaskaet al.displayed the robust quantum state transfer via topologically protected edge pumping in a two-dimensional topological spin system.Meiet al.[44]showed robust quantum state transfer via topological edge states in superconducting qubit chain.Zhenget al.[46]proposed an effective scheme to realize robust quantum state transfer with the topological protected channel in a superconducting flux qubit chain with controlling by defect.In addition,Qiet al.[47]studied the one-dimensional modulated Su-Schrieffer-Heeger chain and implemented the various kinds of topological routers.However,the realization of the topological channel with multiple functions in practical applications is still an open question.Regretfully,most of the previous studies only involve a single quantum state transition.
Motivated by the discussions mentioned above, we construct a topological channel in an extended SSH model with four-period hopping coefficients in one unit cell, dubbed SSH4,to study the robust quantum state transfer.In our multiband system,the topological channel is determined by the gap state protected by the energy gap,in which the particle initially accommodated at the last lattice site will arise in the first and all even lattice sites equally.Then, a multi-port router, being immune to mild-disorder,can be realized if we treat those sites as ports.Further, the probability of the second lattice sites in every unit cell will reduce to zero in certain cases, which demonstrates that a new topological router can be obtained.In addition, our SSH4 model can have the application of 1/3 beam splitter.Namely,the particle occupied at the first lattice site will appear with equal probability at three lattice sites with time evolution.This system can realize a 1/2 beam splitter.Our four-period SSH model can engineer two kinds of quantum optical devices,which is of great significance for quantum information processing.
This paper is organized as follows.In Section 2 we present the extended SSH4 chain with four-period hopping coefficients in one unit cell.In Section 3 it is demonstrated that our multi-band system can realize different types of topological routers with multiple output ports and we explore the effect of the third intracell hopping strength on topological router.In Section 4 we display that our model can realize a 1/3 and 1/2 topological beam splitter.Finally,the conclusions are presented in Section 5.
2.The four-period SSH chain
We consider a one-dimensional four-period SSH chain comprised of 4N+1 lattice sites, withNeven, as schematically shown in Fig.1.In this chain, each unit cell contains four lattice sites labeled byA,B,C, andD, respectively.The extended SSH chain can be described by
whereC†n,Q(Q=A,B,C,D) andCn,Qare the creation and annihilation operators on sublatticesA,B,C,Dof thenth unit cell;t1,t2andt3are the intracell hopping amplitudes;t4is the intercell hopping amplitude.The long-range hopping strengths are represented byJnin which the first siteA1can jump to an arbitraryA-type site in thenth unit cell.For the sake of simplicity, we choose the long-range hopping amplitudesJ1=J2=···=JN ≡Jin this study.

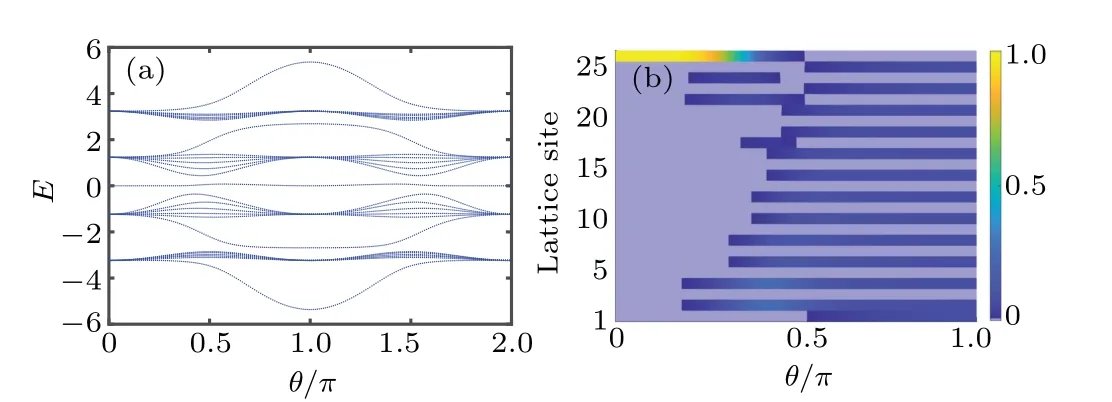
Fig.2.(a) The energy spectra of the generalized SSH chain with t1 = 1+cosθ, J =t4 = 1-cosθ and t2 =t3 = 2.It always has a gap state.(b) The corresponding state distribution of gap state.When θ =0, the gap state gathers toward the last lattice site but θ =π, the gap state localizes at the site of A1,B1,D1,...,and DN.
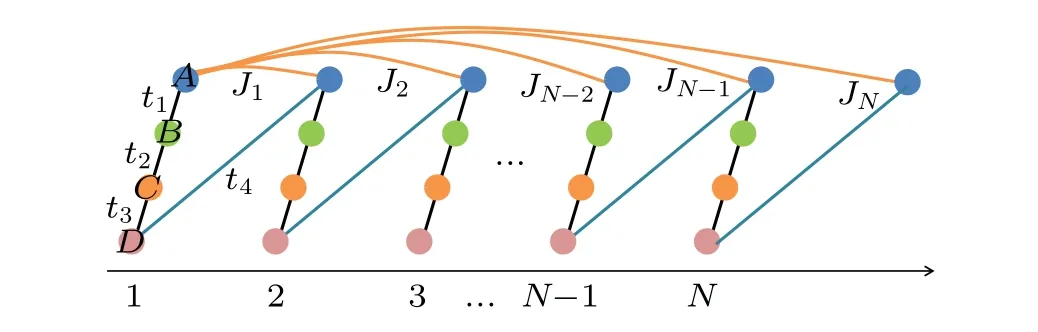
Fig.1.Schematic diagram of the one-dimension extended SSH chain with odd number L = 4N+1.Here, N is the number of unit cell and each one contains four lattice sites labeled by An, Bn,Cn, and Dn(n=1,2,...,N).The intracell hoppings are t1,t2,and t3,respectively.The intercell hopping is t4,and the long-range hopping is Jn.
3.Different types of topological router in fourperiod SSH chain
In this section, we take the parametert1= 1+cosθ,t2=2,andt4=J=1-cosθ.Next,the quantum state transfer will be explored by selecting different values oft3.
3.1.Topological router induced by t3=t2
In this subsection,we focus on a strong intracell hoppingt3=t2=2.The corresponding energy spectrum,as shown in Fig.2(a),always has a state in the energy gap,which provides a cornerstone to realize the robust quantum state transfer.Further, the distribution of the gap states with the varying ofθis displayed in Fig.2(b).It can be found that the gap state is occupied at the last site whenθ=0, whereas it is equally
To further estimate this result,we take the parameterθas 9


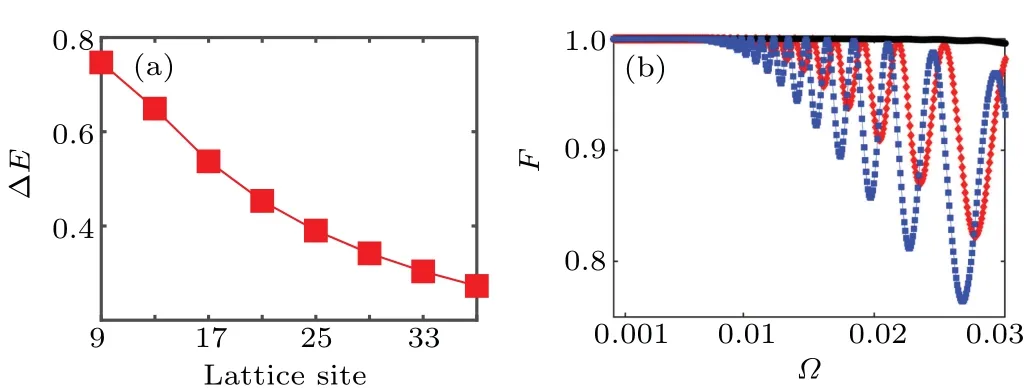
Fig.3.(a)The energy gap(the gap state and the up band)ΔE versus the size of the lattice site.(b)The fidelity of the topological router versus the ramping speed Ω.The black circle, red triangle and blue square lines correspond to the size of the lattice as L=9,L=25,and L=29,respectively.Other parameters are t1 =1+cosθ, J =t4 =1-cosθ,and t2=t3=2.
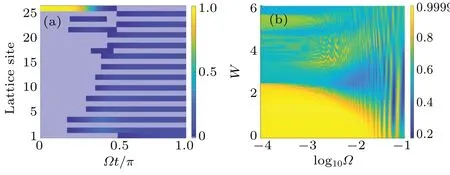
Fig.4.(a)The state transfer process of|0,0,0,...,0,1〉corresponding to Ω =0.0038.(b) The fidelity between the evolved final state and the ideal final state versus the ramping speed Ω and disorder W.Here,t1=1+cosθ,J=t4=1-cosθ,and t2=t3=2.
Finally, we note that there always exists imperfection in the real system, such as defects and impurities.The Hamiltonian with imperfection, i.e., on-site disorder, has the form of
whereWis the strength of the disorder, andδis a random number in the range of [-0.5,0.5] uniformly.In this case, the fidelity between the evolved state and the ideal final state versus the ramping speedΩand the disorder strengthWis numerically displayed in Fig.4(b).The yellow regions undoubtedly show that, for the slow enough ramping speed log10(Ω)<-2.5 and the disorder strengthW<2.5,the state transfer between|Ψ〉iand|Ψ〉fcan be realized with high fidelity.
3.2.A topological router by t3=0.015
We have demonstrated that a multi-port topology router can be formed ift3=t2=2.In this subsection, we take the parametert3=0.015 to explore the quantum state transfer.


Fig.5.(a) The energy spectra of the generalized SSH chain with t1 =1+cosθ, J =t4 =1-cosθ and t2 =2 and t3 =0.015.(b) The distribution of gap state.(c) The fidelity of the state transfer between the evolved final state and the ideal final state versus the varying rate of θ.(d)The state transfer process corresponding to Ω =10-5.
To further confirm this result, we plot the fidelity of the state transfer versus the ramping speedΩ, as shown in Fig.5(d).A smallΩis required to meet the adiabatic evolution condition since the energy gap is narrow at this point.Moreover,to make the results more intuitive,in Fig.5(e),we choose an appropriate value ofΩ=10-5.This numerical result reveals exactly the state transfer between|Ψ〉iand|Ψ〉f.Compared with Fig.4(a), we find that whent3reduces to a small value, the probability of the second lattice site in every unit cell will reduce to zero,by which a new topological router can be induced.
The processes mentioned above can be comprehended as follows.Whenθ= 0, all intracell hopping amplitudes are large than intercell hopping and long-range hooping amplitudes,namely,t1,t2,t3>t4=J,which leads to the four sublattice sites belonging to one unit cell and the final lattice being isolated.Hence,all states locates at the last site.On the other hand,whenθ=π,An,A1,andDnconstitute a domain wall.[48]Therefore,the sitesA1andDncan be isolated.Finally,the gap state is localized at sitesA1,D1,...,andDnuniformly.
From above all, two types of topological routers can be realized in our SSH4 model,only via designing the third intracell hoppingt3appropriately.Therefore, we can control this parameter to realize the distribution of information to some ports.
4.The topological beam splitter
We have discussed the impact oft3on the topological channel.Here, we propose the question for our long SSH4 chain: if other parameters are changed,is there a new channel for state transfer precisely? In the following, the parameterst1andt4change ast1=J=1-cosθandt4=1+cosθ, respectively.We find that, in this set of parameters, our SSH4 system can functionally implement the 1/3 and 1/2 topological beam splitter similar to traditional beam splitter[49-52]in quantum optics.
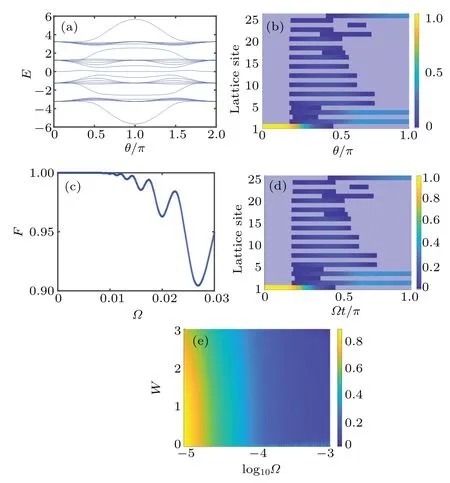
Fig.6.(a) The energy spectra of the extended SSH chain with t4 =1+cosθ, J =t1 =1-cosθ, t2 =t3 =2.(b) The corresponding the distribution of gap state.(c) The fidelity of the state transfer between|1,0,0,...,0,0〉and|0,1/3,0,1/3,0,0,...,0,0,1/3〉versus the varying rate of θ.(d) The state transfer process corresponding to Ω =0.006.(e)The fidelity between the evolved final state and the ideal final state versus the ramping speed Ω and disorder W.
4.1.The 1/3 topological beam splitter
Under this condition,we further chooset2=t3=2 to investigate the state transfer.As shown in Fig.6(a), the energy spectrum tells us that the gap state always exists in our long SSH4 chain.The corresponding distribution of the gap state is shown in Fig.6(b).It can be found that the gap state is mainly localized at the first site inθ=0, and yet it will pile up at the second, the fourth and the last sites with the same probability inθ=πeventually.One can then get some information that, through the gap state, the state transfer between the state|1,0,0,...,0〉and|0,1/3,0,1/3,0,...,0,0,1/3〉can be achieved.To estimate the above result more precisely,one can takeθ=Ωtand utilize the time-dependent Hamiltonian to evolve the initial state|1,0,0,...,0〉.In Fig.6(c), the fidelity between the ideal state|0,1/3,0,1/3,0,...,0,0,1/3〉and the evolved final state versus the parameterΩis displayed.The numerical results clarify that some value ofΩcan ensure the achievement of the state transfer between the initial state and evolved state.A concrete example can be revealed in Fig.6(d)withΩ=0.006,and we find that the state initially in the first site can be transferred to the second,the fourth and the last site with the same distributions.
As we explained above, the process of the realization of the topological router is immune to on-site disorder.Here,we also numerically show that the effect of the on-site disorder on our beam splitter.The disorder has the form of∑nWδ(C†n,ACn,A+C†n,BCn,B+C†n,CCn,C+C†n,DCn,D) (withWbeing the disorder strength andδbeing the a random number within [-0.5, 0.5]).In Fig.6(e), the fidelity between the evolved state and the ideal final state is displayed versus the ramping speedΩand the disorder strengthW.It can be found that the state transfer between|Ψ〉iand|Ψ〉fcan be realized with high fidelity under slow enough ramping speed and mild disorder.

Fig.7.(a) The energy spectra of the generalized SSH chain with t1=1+cosθ,J=t4=1-cosθ,t2=0.015,and t3=2.(b)The energy gap at θ ∈[0,0.3π].(c)The distribution of gap state.(d)The fidelity of the state transfer between the evolved final state and the ideal final state versus the ramping speed Ω.
4.2.The 1/2 topological beam splitter
Analogously, one can chooset2=0.015 andt3=2.In Figs.7(a)and 7(b),there always possess the energy gap even thought2is small,which can be used as a topological channel to achieve topological state transfer.As shown in Fig.7(c),we plot the distribution of the state withθ.It can be found that the initial state (θ=0) lies in the first sites while the final states(θ=π)occupy the second and the last sites,which illustrates that the gap state can be served as a channel to actualize a 1/2 beam splitter.[49]Further, to prove our idea, one can chooseθ=Ωtand numerically calculate the fidelity in Fig.7(d).It can be found that the fidelityF=1 whenΩis small, implying that our SSH4 system can functionally implement the 1/2 topological beam splitter.
5.Conclusion
We have constructed an SSH4 model containing four periods of the hopping coefficients to investigate robust quantum state transfer.A topologically protected channel where the particle initially pinned at the last lattice site and finally appeared equally at multiple lattice sites can be formed.Then,a multi-port router can be realized provided that we treat those sites as ports.Moreover, the transfer fidelity displays a wide plateau at the value of unity even if the disorders are considered.When the third intracell hopping reduces to a small value, it can generate a new topological router in which the occupancy probability of all the second lattice sites becomes zero.In addition, the long SSH4 chain can have the function of a 1/3 beam splitter.Namely,the particle initially occupies the first lattice site and finally appears with equal probability at three lattice sites.We can also realize a 1/2 beam splitter.The SSH4 system may play a key role in multiple function topological channel,which is vital in quantum information processing.Our four-period SSH model can engineer two kinds of quantum optical devices,which provides the potential applications for topological quantum information processing.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.11874190, 61835013, and 12047501), and the Supercomputing Center of Lanzhou University.
杂志排行
Chinese Physics B的其它文章
- Matrix integrable fifth-order mKdV equations and their soliton solutions
- Comparison of differential evolution,particle swarm optimization,quantum-behaved particle swarm optimization,and quantum evolutionary algorithm for preparation of quantum states
- Explicit K-symplectic methods for nonseparable non-canonical Hamiltonian systems
- Molecular dynamics study of interactions between edge dislocation and irradiation-induced defects in Fe-10Ni-20Cr alloy
- Spontaneous emission of a moving atom in a waveguide of rectangular cross section
- Novel traveling quantum anonymous voting scheme via GHZ states
