Novel traveling quantum anonymous voting scheme via GHZ states

Wenhao Zhao(赵文浩) and Min Jiang(姜敏)

1School of Electronics&Information Engineering,Soochow University,Suzhou 215006,China

2Key Laboratory of System Control and Information Processing,Ministry of Education,Shanghai 200240,China

Keywords: quantum anonymous voting,quantum secure communication,GHZ states,verifiability,privacy

1.Introduction

Voting is a significant way of decision-making in politics,economics and people’s daily life.With the development of communication science and technology, various voting technologies have been developed rapidly in terms of voting form,security, and efficiency.Nowadays electronic voting is very popular, whose security depends on the computational complexity of solving mathematical problems.However,in recent years, with the development of quantum chips and quantum computers,[1]classical cryptography has to consider the security risks brought by“quantum threats”.

Based on the laws of quantum mechanics,during the past years,many efforts have been devoted to the research of quantum anonymous voting (QAV) in order to design a high secure voting scheme.Furthermore,the fundamental researches of quantum computation and information, such as quantum teleportation,[2,3]quantum states preparation,[4,5]and quantum memory for free,[6,7]have laid a foundation for the implementation of quantum voting schemes.In 2005,Christandl and Wehner[8]proposed a quantum communication protocol that could anonymously transmit classical bits using shared quantum states and classical broadcast channels, which was the first time that quantum anonymous voting was proposed.Later, Hilleryet al.[9]proposed two kinds of quantum voting modes: the traveling ballot mode[10-14]and the distributed ballot mode.[15-21]In 2011, Bonanomeet al.[22]presented a modified QAV protocol on the basis of Hillery’s voting protocol,which improved privacy protection in voting and examined the security of protocol under certain types of attacks.In the following years, various QAV schemes have been proposed based on the traveling voting mode.Most existing traveling QAV schemes have some security deficiencies that cannot avoid repetitive voting and voters cannot verify the voting results.

In 2020, Shiet al.[23]proposed a traveling QAV protocol based on the Chinese remainder theorem.In their scheme,the voters could verify the correctness of their votes.However, in the initial and verification phase of his scheme, the voter’s identity information and the corresponding voting content were broadcast by classical encryption and classical channels.If the eavesdropper used quantum computing to eavesdrop on the voting information, the voters’ identity information and voting content would be leaked, and the privacy would not be guaranteed.As a matter of fact, in most traveling quantum anonymous voting schemes,the voters have only two options “yes” or “no” to choose.It is important to improve its scalability in various voting scenes.Recently, Liet al.[24]adopted grouping strategy to improve the efficiency of distributed quantum voting protocol.Hence, it is worth considering how to adopt grouping strategy to improve the practicality of our traveling quantum anonymous voting scheme.

In this paper, we present a secure traveling quantum anonymous voting scheme via Greenberger-Horne-Zeilinger(GHZ)states.Our traveling QAV scheme satisfies the following features: (i) Privacy: The identity information of each voter and its corresponding voting information are known only to himself/herself, and other participants cannot obtain it.(ii) Verifiability: After the voting closes, according to the final announcement information, each voter can verify whether his/her voting content is correctly counted.(iii)Nonrepeatability: Each voter is only allowed to cast one vote and cannot vote more than once,and so on.These are also the three most important principles in voting scheme.Furthermore,the security analysis shows that our voting scheme can resist various attacks.

The remainder of this paper is structured below: In Section 2,we briefly introduce the primary preliminaries.In Section 3, we elaborate the proposed traveling quantum anonymous voting scheme.In Section 4, we analyze the security of the proposed protocol from several aspects.Then the Section 5 shows the comparisons between existing schemes and ours from several aspects.Finally,we give a short conclusion in Section 6.

2.Preliminaries

Ind-dimensional Hilbert space,a single particle has two kinds of common orthonormal bases: the computational basisBC={|0〉C,|1〉C,|2〉C,...,|d-1〉C}and the fourier basisBF={|0〉F,|1〉F,|2〉F,...,|d-1〉F}.The fourier basis can be obtained by the quantum fourier transformFon the computational basis,which can be defined as

where|k〉C∈{|0〉C,|1〉C,|2〉C,...,|d-1〉C}.

The three-particled-level Greenberger-Horne-Zeilinger(GHZ)state in Fourier basis can be defined as

|ψ〉0,1,2has an interesting property[25]that it can be written as the following form in computational basis:

Therefore, when each particle of|ψ〉0,1,2is measured in Fourier basis, the measurement outcomes are the same for each particle.When each particle of|ψ〉0,1,2is measured in computational basis, the summation of the measurement outcome modulodis always equal to zero.

We introduce ad×dunitary operationUr,[26]which can be described as

wherer ∈{0,1,2,...,d-1}and⊕denotes addition moduled.For example, when the unitary operationUris performed onto thed-level single qubit|k〉Cand|k〉F,these states can be transformed to

wherek ∈{0,1,2,...,d-1}.The unitary operations will be used as the encoding operators in the proposed voting protocol.

When the unitary operationUv(0≤v ≤d-1) andUt(0≤t ≤d-1) are performed onto the first particle and the second particle of the GHZ state|ψ〉0,1,2in the computational basis,the state becomes

If the single-particle measurement with the computational basis is performed onto each particle of state|ψ＇〉0,1,2,we will obtain the measurement outcomesσ0,σ1, andσ2, respectively.The relationship between the measurement outcomes and the parameters of unitary operation can be described as follows:

If we obtain the measurement results of each particle of the state|ψ＇〉0,1,2and the parametertof the unitary operationUt,the parametervof unitary operationUvcan be deduced.This feature can be used to count and verify the voting results in the proposed voting scheme.

3.Description of the proposed QAV scheme

3.1.Procedures of the scheme

In this voting scheme, the quantum voting network is managed by the voting service center (VSC), which wants the real voting results.The teller T has the responsibilities for collecting the voting particle sequence and participating in the counting of votes.Suppose that there are totallymballot items in the voting activity,which are encoded as the integers 0,1,2,...,m-1.Each legitimate voterVi(i=0,1,2,...,n-1)can select a vote object from the set{0,1,2,...,m-1}.The diagram of the voting process of the traveling anonymous voting scheme is shown in Fig.1.

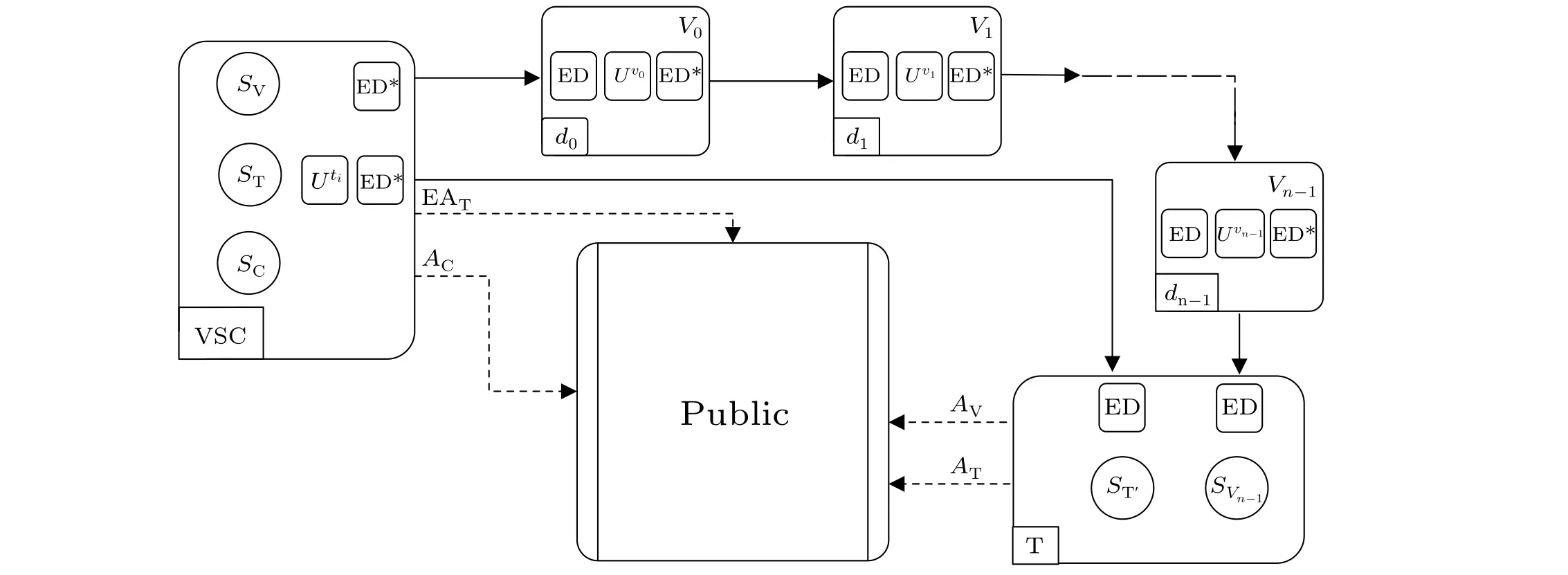
Fig.1.The flow diagram of the proposed traveling anonymous voting scheme voting.ED and ED∗indicate the eavesdropping detection. Ux indicates the unitary operation.The solid lines and dashed lines indicate the quantum channel and the classical channel,respectively.

3.1.1.Initial phase

Step 1The citizens send the identity information and the voting application to the VSC.The VSC checks whether the citizen is legal and whether the citizen is applying to vote for the first time.Assume that the number of legal voters who pass the checking isn.

Step 2Each legal voterViobtains a unique private indexdibased on quantum random draw protocol.[27]According to the indexdi, the voter will perform the unitary operation to encode in corresponding position in follow-up steps.

Step 3The VSC preparesncopies ofm-level GHZ states|ψ〉0,1,2and picks up all the qubit labels with 0s,1s,and 2s to compose the ordered particle sequences[28]SV,ST, andSC,respectively.After that, the VSC performs the unitaryUtion each particle of sequenceST, in which eachtiis a random number chosen from the set{0,1,...,m-1}.At the same time, the VSC records the parameters of the unitary operationUtiand their corresponding positions as the array EAT={t0,t1,...,tn-1}.Before transmitting the particle sequencesSVandST＇,the VSC randomly generates enough decoy single qubits from the basisBCorBF,and inserts them into the sequencesSVandST＇, respectively.The VSC will obtain the new particle sequencesS∗VandS∗T＇.Then the VSC keeps the sequenceSCand sends the sequenceS∗T＇,S∗Vto the teller T and the first voterV0,respectively.

3.1.2.Voting phase

Step 1After confirming that the voterV0has received the sequenceS∗V,the VSC declares the initial states and the corresponding insertion positions of decoy particles toV0by classical channel.The voterV0measures the decoy particles with the corresponding measurement basis and calculates the error ratio by comparing with the initial states.If the error ratio is greater than the secure threshold, the process will be stopped and restarted.Otherwise,the process will continue.

3.1.3.Counting votes phase

fori=0,1,2,...,n-1.

3.1.4.Verifying phase

When obtaining the arrayζ, each voterVican verify whetherrdi=vi.If the answer is yes, the vote contentviof voterViis correctly counted.Otherwise,Vianonymously broadcasts an aborted signal.Once there is an aborted singal,the voting protocol will be aborted and the voting results will be abandoned.

3.2.Grouping strategy

For the proposed traveling quantum anonymous voting scheme, with the number of voters increasing, it will take more time to complete the voting process.We can adopt voter grouping strategy and candidate grouping strategy to improve the practicality and flexibility of voting.

4.Security analysis

4.1.Intercept-resending attack

Hereuis the number of decoy particles for each eavesdropping detection;iis thei-th decoy single particle;Pi(BC) indicates the probability of choosing the measurement basisBC;Pi(R|BC) indicates the conditional probabilities of passing eavesdropping detection;P(BF) indicates the probability of choosing the measurement basisBF;Pi(R|BF)indicates the conditional probabilities of passing eavesdropping detection.The probabilitites that the eavesdropper guesses the measurement basisBCandBFare 1/2 and 1/2,respectively.No matter which measurement basis is guessed, the conditional probability of passing the eavesdropping detection is 1/m.For each decoy particle,the intercept-resending attack cannot be dected with the probability of 1/m.Because there are totallyudecoy particles,the intercept-resending attack cannot be dected with the probability(1/m)u.Therefore,the intercept-resending attack will be discovered with probability 1-(1/m)u,which approaches infinitely 100% with the number of decoy particles increasing.

4.2.Measure-resending attack

During the sequence transmission, an eavesdropper may also launch the measure-resending attack.The main difference between measure-resending attack and interceptresending attack is that the eavesdropper selects a measurement basis to measure the tranmitted sequence in measureresending attack.According to the measurement results, the eavesdropper prepares one fake particle sequence.The probability that the measure-resending attack is deteced by eavesdropping detection can be described as

Hereuis the number of decoy particles for each eavesdropping detection;iis thei-th decoy single particle;Pi(S) andPi(F) indicate the probability of guessing the correct measurement basis and guessing incorrect measurement basis,respectively;Pi(R|F) indicates the conditional probability of passing eavesdropping detection.The eavesdropper does not know any information about decoy particles.For each decoy particle, the probabilities of the eavesdropper guessing correct and incorrect measurement basis arePi(S)=1/2 andPi(F)=1/2,respectively.When the correct measurement basis is used,it will pass the eavesdropping detection.When the incorrect measurement basis is used, the conditional probability of passing eavesdropping detection isPi(R|F)=1/m.For this decoy particle, the measure-resending attack cannot be dected with probability (1/2)+(1/2m).Because there areudecoy particles,the probability that measurementresending attack cannot be dected is [(1/2)+(1/2m)]u.The intercept-resending attack will be discovered with probability 1-[(2m+1)/(2m)]u.As the number of decoy particles increases,this probability approaches infinitely 100%.

4.3.Entangle-measure attack

If the eavesdropper wants to perform the entanglemeasure attack,[30]he/she needs to perform the unitary operationUeonto the intercepted qubit to make it entangle with the auxiliary photon|e〉.The unitary operationUethat causes the transmitted qubit to interact coherently with an ancillary qubit|e〉can be defined as follows:

4.4.Collusive attack

Assume several dishonest voters intend to refuse the honest voter to take part in voting.For instance, the dishonest votersVjandVj+2do not want the honest voterVjto participant in voting.The voterVjdirectly sends the real ballotS∗VjtoVj+2and sends a deceptive ballotSDVjtoVj+1.After the voterVj+1finishes his voting operation,he sendsSDVj+1to the next voterVj+2.As a legal voter, the voterVj+1can obtain a private unique indexdj+1before starting voting.In the verifying phase,if the voterVj+1find that the elementrd j+1of the arrayζis not equal his expected item, he will anonymously broadcast an aborted signal.

4.5.Privacy

The privacy is the most primary property for QAV protocol.In our scheme,each voter has a unique and private index and other voters cannot get this index.According to the private index, each voter performs the unitary operation on corresponding positions in the ballot state sequence.Although all voting data is open,each voter’s voting content is only known by himself/herself.Therefore, the anonymity and privacy of voters can be guaranteed.

4.6.Verifiability

Each voterVican verify whetherrdiis equal tovi.If the answer is yes,Vi’s expected item is correctly expressed.Otherwise, each voter can check that whether his voting content has been tampered by the attacker.Hence, this ensures that if a dishonest voter tampers with the content of other honest voters,the dishonest behavior will be perceived.

4.7.Non-repeatability

Each voter has a unique and private index and other voters cannot get this index.If one voter wishes to vote twice or more times, he will perform unitary operation on other particles of sequence,which influences the content of votes cast by legal voters.In verifying phase,each voterViverifiesrdi=vito make sure that his voting content has not benn tampered.If the honest voters are awared of the risk,the voting process will be aborted.

5.Comparison

The comparisons between several traveling QAV schemes[10,11,13,22,23]and our scheme can be seen in Table 1.Our traveling QAV scheme can ensure basic voting principles,including privacy, verifiability and non-repeatability.In addition, our traveling QAV scheme also supports customizing the number of ballot items,and is suitable for the voting scene with a good deal of ballot items.

Table 1.Comparisons of different schemes in several aspects.

6.Conclusion

In this paper, we proposed a secure traveling quantum anonymous voting with GHZ states.The proposed traveling quantum anonymous voting scheme can be applied to the voting scene with a large amount of ballot items.In order to improve the efficiency of the traveling quantum anonymous voting scheme,we proposed an optimization method based on grouping strategy.Compared with the most existing traveling quantum voting schemes,the proposed scheme has higher security, which is manifested in its privacy, verifiability, and non-repeatability.Finally,the security analysis shows that the proposed traveling quantum anonymous voting scheme can resist various attacks and have good safety.

Acknowledgments

Project supported by the Tang Scholar Project of Soochow University, the National Natural Science Foundation of China (Grant No.61873162), the Fund from Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network and Suzhou Key Laboratory of Advanced Optical Communication Network Technology.