Tightly focused properties of a partially coherent radially polarized power-exponent-phase vortex beam
2023-03-13KangChen陈康ZhiYuanMa马志远andYouYouHu胡友友
Kang Chen(陈康) Zhi-Yuan Ma(马志远) and You-You Hu(胡友友)
1Department of Optoelectronic Information of Science and Engineering,School of Science,Jiangsu University of Science and Technology,Zhenjiang 212100,China
2Applied Optics Research Center,Jiangsu University of Science and Technology,Zhenjiang 212100,China
Keywords: partially coherent beam,power-exponent-phase vortex beam,tight focusing properties
1.Introduction
Vortex beams, characterized by the spiral phase factor exp(ilφ), are the important members of structured beams, of which each photon possesses a well-definedlħ orbital angular momentum(OAM).[1,2]Because of this special characteristic,the focusing properties of vortex beams have been extensively studied.[3-5]The power-exponent-phase vortex(PEPV)beam is a new kind of vortex beam that is characterized by a power-exponent-phase exp[i2lπ(φ/2π)n].It was proposed by Zhaoet al.for the first time[6]and the evolutions of the intensity distribution of such a beam in free space and a focusing system were investigated in detail.[7]The PEPV beam has an asymmetric intensity distribution and,during propagation,the intensity rotates and gathers along the ring.[7]Therefore, PEPV beams have unique applications in particle capture and manipulation, which can not only capture two different types of particles at the same time,[8]but also automatically transport particles along the curved path and avoid obstacles.[9]In addition, the PEPV beam has stronger antiinterference when propagating in ocean turbulence.[10]Therefore,further research on PEPV beams is of great significance.
In addition, with the development of cylindrical vector beams,[11]radially polarized beams have attracted considerable attention because they can produce very small focal spots,and generate longitudinal electric-field components upon focalization.[12,13]And the combination of a radially polarized beam and a PEPV beam has been proven to have unique advantages in particle manipulation.[7,14]
On the other hand, besides intensity, polarization and phase, the beam itself has another important controllable parameter called coherence.Results indicate that spatial coherence of a partially coherent beam has important effects on the tight focusing characteristics,especially the fact that the transverse field distribution can be changed by changing the initial coherence width.[15-17]In previous work,we investigated the propagation properties of a partially coherent PEPV beam and obtained interesting results.[18]Therefore, the combination of a radially polarized PEPV beam and a partially coherent beam can combine their characteristics, which can make the advantages of the PEPV beam in some applications more obvious.However, to the best of our knowledge, research on the tight focusing properties of partially coherent radially polarized PEPV beams has not been reported.
In this paper, a partially coherent beam called a radially polarized multi-Gaussian Schell-model power-exponentphase vortex (MGSM-PEPV) beam is proposed.Based on the unified theory of coherence and polarization,a theoretical model of partially coherent radially polarized PEPV beams is established.Then, the tight focusing properties of the beam passing through a high numerical aperture(NA)objective lens was numerically studied, including the relationship between the correlation function, power order, topological charge and coherence width.This study will lay a theoretical foundation for the application of radially polarized MGSM-PEPV beams in optical capture and other fields,which is of great importance for promoting the theory and application of partially coherent radially polarized PEPV beams.
2.Radially polarized multi-Gaussian Schellmodel power-exponent-phase vortex beam
In the spatial frequency domain, under the unified theory of coherence and polarization, the cross-spectral density(CSD)matrix is utilized to characterize the second-order statistical properties of partially coherent vector beams.In the source plane, the elements of the CSD matrix are expressed as[19,20]
wherer1=(x1,y1)andr2=(x2,y2)are the position vectors at the source plane,andEα(r)andEβ(r)denote two orthogonally stochastic electric field components along thexandyaxis,respectively.Here,“∗”is the complex conjugate and“〈〉”indicates the ensemble average.For the sake of simplicity,this article will omit the dependence of the CSD matrix and other derived variables onω.
In this paper,we mainly study the power-exponent-phase vortex beam[6]
The multi-Gaussian Schell-model beam CSD function can be obtained from[21,22]
Here,
is the normalized factor,Mis the number of Gaussian functions, andδαβis the feature source correlations.Meanwhile,Aαis the amplitude in theαdirection andBαβis the singlepoint correlation coefficient.For the convenience of calculation,we letAαequal to 1.
Meanwhile, the conditions that the radially polarized source must satisfy areBαβ=1 andδα=δ0.[23]Then, by combining Eqs.(2) and (3), we can obtain the CSD matrix elements of the radially polarized MGSM-PEPV beam
whereδ0represents the spatial coherence width.
3.Tight focusing properties of a radially polarized multi-Gaussian Schell-model powerexponent-phase vortex beam
Figure 1 shows the scheme of the radially polarized MGSM-PEPV beam passing through a high NA objective lens.Based on the Richards-Wolf vectorial diffraction integral, in the cylindrical coordinate system, when the beam passes through the high NA objective lens,the vector electric field in the focal region can be written as[23,24]
where (r,φ,z) are the cylindrical coordinates,φis the azimuthal angle of the incident beam,θis the NA angle,αis the maximal NA angle given by the formulaα=arcsin(NA),k=2π/λis the wave number withλbeing the wavelength of the incident beam,Ax(θ,φ) andAy(θ,φ) are the pupil apodization functions at the aperture surface,andfis the focal length of the high-NA objective lens.
The conversion between rectangular coordinates and cylindrical coordinates can be calculated using the following relationship:[25]
The statistical characteristics of the radially polarized MGSM-PEPV beam on the focal area can be represented by a 3×3 CSD matrix,and the elements can be written as

Fig.1.A scheme showing the tight focusing of a light beam focused by a high-NA objective lens.
By settingr1=r2=randφ1=φ2=φ, we can obtain the transverse, longitudinal and total component of the focal intensity in the focal area
4.Numerical calculation and analysis
4.1.Intensity analysis
Next, based on MATLAB R2020b software, the related calculation programs are written to numerically study the tight focusing characteristics of the radially polarized MGSMPEPV beam.The Parallel Computing Toolbox,combined with GPU,is applied to accelerate the calculation.The comparison results show that the calculation using the Parallel Computing Toolbox is nearly 7 times faster than the direct numerical calculation.Our method greatly improves the calculation speed.In the following numerical examples, we setλ=632.8 nm,w0=1 mm,f=3 mm,and NA=0.95.
Figure 2 shows the total intensityItotal, transverse intensityItra,and longitudinal intensityIzof the tightly focused radially polarized MGSM-PEPV beam in the focal plane with different values of beam indexM.It can be seen that the distribution of the total intensity is similar to the longitudinal intensity distribution,which indicates that the longitudinal component is dominant in the total intensity.And it can be clearly seen that as the beam index increases, the outer ring of the spot gradually disappears,and the contour of the spot becomes clearer and smoother,which is due to the influence of the special correlation function(i.e.,the multi-Gaussian Schell-model correlation function).
Then, we mainly study the influences of the coherence widthδ,the topological chargeland power ordernof the radially polarized MGSM-PEPV beam on the total intensity distribution in the focal region.Figure 3 shows the total intensity distribution of a tightly focused radially polarized MGSMPEPV beam with different values of topological chargeland coherence widthδ.It clearly shows that the beam intensity profile gradually degenerates into a Gaussian profile and a flattopped shaped focal field with the decrease of the coherence width.This may be because the effect of topological charge on the focal intensity distribution will be weakened with the decrease of the coherence width.When the topological chargelis large(i.e.,l=8),an opening gradually appears in the light spot with the increase in coherence lengthδ.Similarly,when the coherence width is large(i.e.,δ=5), the light spot gradually increases and an opening appears with the increase in the topological charge number.This non-uniform asymmetric focal spot will help trap irregular particles or manipulate absorbing particles.[26]

Fig.2.Intensity distributions of the total intensity Itotal, transverse intensity Itra,and longitudinal intensity Iz of a tightly focused radially polarized MGSM-PEPV beam with coherence width δ =5 mm,topological charge l=2 and power order n=2 in the focal plane for different values of beam index M.

Fig.3.The total intensity distribution of a tightly focused radially polarized MGSM-PEPV beam with the beam index M=7 and power order n=2 in the focal plane for different values of topological charge l and coherence width δ.
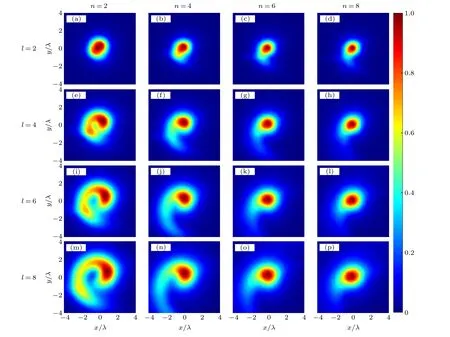
Fig.4.The total intensity distribution of a radially polarized MGSM-PEPV beam with the beam index M=7 and the coherence width δ =5 in the focal plane for different topological charges l and power order n.
Next, we show the total intensity distributions of the tightly focused MGSM-PEPV beam with different values of power ordernand topological chargelin Fig.4.It can be seen that when the power ordernis small (i.e.,n=2), with the increase in the topological chargel,the light spot gradually increases and an opening appears.At the same time,with the increase in the power ordern,the intensity gradually concentrates in the upper part and the lower part vanishes.It can be seen from Eq.(2)that asnincreases,the phase term is almost constant, and the beam profile becomes Gaussian.[7]Therefore,whennis large enough,the beam gradually evolves into a Gaussian beam.In addition,the literature[12]performed numerical simulations on the energy flow of the PEPV beam under different parameters,and the results showed that the light energy was shrinking around the ring.By combining the results of Fig.4, it can be shown that the light spot gradually concentrates on one point along the ring.This unique property can automatically transport particles along a curved path,and the existence of openings can help avoid obstacles.
4.2.Analysis of polarization and coherence
The degree of polarization and coherence are important components of the vector partially coherent beam.In this section,we mainly study the degree of polarization and coherence of a tightly focused MGSM-PEPV beam with the topological chargel=8 and power ordern=2 in the focal plane.
The degree of polarization of the tightly focused partially coherent PEPV beam in the focal plane can be expressed as[25-27]
The degree of polarization can be used to describe the depolarization characteristics of the tightly focused radially polarized MGSM-PEPV beam in the focal plane.WhenP=1,it indicates that the tightly focused beam is a completely polarized beam;whenP=0,it indicates that the tightly focused beam is a completely unpolarized beam; when 0<P<1,it indicates that the tightly focused beam is a partially polarized beam.
The degree of coherence between any two orthogonal field components of the tightly focused MGSM-PEPV beam in the focal plane can be expressed as[24,27]
When 0<|µij(r,φ,z)|<1, the two components are partially coherent;when|µij(r,φ,z)|=1,the two components are completely coherent; and when|µi j(r,φ,z)|=0, the two components are completely incoherent.
Figures 5 and 6 show the degree of polarization distribution of a radially polarized MGSM-PEPV beam in the focal plane under different coherence lengths and beam indices,respectively.
From Eq.(13), we can find that the degree of polarization of the radially polarized MGSM-PEPV beam is uniform on the source plane.It can be seen from Figs.5 and 6 that both the beam index and the coherence width have a certain effect on the degree of polarization of the tightly focused beam.In Fig.5,we can see that the degree of polarization of the tightly focused radially polarized MGSM-PEPV beam becomes nonuniform across the focal plane, and its value does not equal 1 in most parts of the focal plane,which means the tightly focused radially polarized MGSM-PEPV beam is depolarized in the focal plane,and the depolarization of the lower half of the focal zone is more obvious.The properties of the depolarization are closely determined by the initial coherence of the radially polarized MGSM-PEPV beam.Moreover,one finds from Fig.6 that the distribution of the degree of polarization is also closely related to the beam indexM.Therefore,we can control the polarization properties of the tightly focused radially polarized MGSM-PEPV beam by choosing suitable values of the coherence width and beam index.

Fig.5.The degree of polarization of partially coherent radially polarized PEPV beams with the beam index M=7,topological charges l=8,and power order n=2 for different coherence widths δ.

Fig.6.The degree of polarization of partially coherent radially polarized PEPV beams with the coherence width δ =5,topological charges l=8,and power order n=2 for different beam indexes M.

Fig.7.The degree of coherence of partially coherent radially polarized PEPV beams with the beam index M=7,topological charges l=8,and power order n=2 for different coherence widths δ.

Fig.8.The degree of coherence of partially coherent radially polarized PEPV beams with the coherence width δ =5,topological charges l=8,and power order n=2 for different beam indexes M.
Figures 7 and 8 show the degree of coherence between the components of a partially coherent radially polarized MGSMPEPV beam with different coherence widths and beam indexes in the focal plane,respectively.It can be seen from Figs.7 and 8 that the coherence length has a great influence on the coherence distribution of the tightly focused partially coherent radially polarized MGSM-PEPV beam and,as the coherence width increases, the degree of coherence gradually weakens.This indicates that the correlation between any two of the three orthogonal electric field components is decreased by the tight focusing.Moreover,the beam index has little influence on the coherence.In addition, it can be clearly seen that the coherence degree of the left half of the focal zone is relatively high.By choosing appropriate values for the initial coherence width and beam index, we can control the coherence of a partially coherent radially polarized PEPV beam.
5.Conclusion
A partially coherent beam called a radially polarized MGSM-PEPV beam in this paper is introduced.Then, the focal intensity distribution of the radially polarized MGSMPEPV beam after passing through a high-NA objective lens was numerically studied.The effects of beam index,topological charge,power order and coherence width on the intensity distribution of the focused spot were studied in detail.We also analyzed the degree of polarization and coherence of the beam in the focal plane.The results show that the beam quality improves with the increase in the beam index,and the focal fields of different structures that include the flattened beam can be obtained by changing the coherence width.In addition,by changing the topological charge and power order,the intensity can gather to a point along the ring.These unique properties will have potential applications in particle capture and manipulation,especially in the manipulation of irregular particles.
Acknowledgment
Project supported by the Natural Science Foundation of Jiangsu Province,China(Grant No.BK20190953).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA
