Quantum mechanical solution to spectral lineshape in strongly-coupled atom-nanocavity system
2022-04-12JianZeng曾健andZhiYuanLi李志远
Jian Zeng(曾健) and Zhi-Yuan Li(李志远)
School of Physics and Optoelectronics,South China University of Technology,Guangzhou 510641,China
Keywords: Rabi splitting,nanocavity,double Lorentzian lineshape
1. Introduction
Experimental approaches to manipulating the interaction between light and matter in the mesoscopic micrometer/nanometer and even microscopic atomic size scales have quickly advanced in recent years and give birth to many new research topics ranging from spontaneous emission control to advanced micro/nano-laser building. Using the stronglycoupled atom-nanocavity system, researchers have made the experimental realization of non-destructive detection of a single photon,[1]nanophotonic quantum phase switch,[2]quantum logical gate,[2-4]and Heralded quantum storage.[5]Similarly,quantum dots can be substituted by atoms for wider applications in the strongly-coupled exciton-nanocavity system,such as photon-sorter[6], photon switch,[4]and high-fidelity quantum-logic gate.[7-10]One of the well-known devices for realizing unique light-matter interaction consists of quantum emitters and a resonant micro/nano-cavity. The strength of interaction can be described by Rabi frequency, the rate of the exchange of energy between light and matter.[11,12]
The weak side of this interaction results in the usual spontaneous emission of an excited atomic state with its population decaying in an exponential way, according to Fermi golden rule. This well-known feature underlies many applications such as the fabrication of fluorescent lamps and lightemitting diodes. Importantly, the rate of spontaneous emission can be accelerated in certain elaborate nanostructures and nano-devices, according to Purcell effect.[13-16]The strong side of this interaction is popularly referred to the strong coupling regime, where many distinct features, phenomena, and laws of light-matter interaction have been discovered. Unlike the exponential energy decay,the rate of energy exchange between light and matter is much faster than that of energy decay through atomic transition and dissipation in a cavity in the strong coupling regime.[17]Therefore,one can observe the energy transfer between the emitter and background electromagnetic field, and it appears as Rabi oscillation, where the emitter shifting back and forth between the ground state and excited state.[18]In this case,the energy level hybridization of matter and light changes the primarily degenerate states into non-degenerate dressed states,[19]showing double peaks in the spectrum known as Rabi splitting. With such a property, the strong coupling of quantum emitter with cavity is important for a wide range of applications and studies, such as quantum cryptography,quantum information processing,[20]nanooptical circuits,[21]single-photon switch,[2]and single-atom laser.[22]
During the past decades, a lot of theory has shown that the coupling effect is proportional to atomic dipole moment and the electric field strength per photon.[19,23,24]The former is related to the emitter, and the latter is related to the resonant cavity. These two entities provide the avenue to realize the strong coupling regime. In terms of the emitter, the most convincing quantum emitter is a single atom.[25-27]However,atom has a too small dipole moment. Moreover, it is a great struggle to fix and manipulate an atom, even with relatively stationary devices.[27,28]Another well-known emitter is the quantum well, which is the first to observe the Rabi splitting in the semiconductor,[29]although the result has been in dispute about whether or not it is the quantum splitting.[25,30]Recently,quantum dots have been widely used to achieve strong coupling because of its relatively large dipole moment.[31-34]For example, putting quantum dots within micropillar cavity with carefully designed Bragg reflector allows one to observe Rabi splitting of 140 µeV,[33]while a single quantum dot embedded within a photonic crystal cavity displays the anti-crossing spectral feature.[34]For plasmonic nanocavity with much smaller geometric and modal volume, molecules are more suitable to serve as emitters.[35]As it is hard to obtain a single molecule, theJaggregates are in more common use.[36-39]For instance,a methylene-blue molecule with a molecular transition at 665 nm can experience a giant Rabi splitting of 380 meV,and a single emitter can generate 95-meV Rabi splitting.[37]
In terms of cavity, experiments and theories have shown that low loss and small effective cavity volume are conducive to reach strong coupling.[40,41]Fabry-P´erot resonance due to two high-reflection mirrors placed opposite to each other, is the most basic kind of optical cavity with small dissipation and high-quality factor.[42-44]Nevertheless,the effective cavity volume of Fabry-P´erot resonance is limited by the minimum resonance wavelength of light, which compromise its application.[45]In comparison, plasmonic metal cavity provide an alternative route to drastically decrease the effective cavity volume for strong coupling,[46,47]benefiting from the collective oscillation of free electron in metal-induced giant local electric field enhancement, and much more easily reach the strong coupling regime compared with Fabry-P´erot microcavity.[48]Tamm plasmon polaritons coupling with surface plasmon polaritons (as plasmonic metal cavity), for instance,are shown to modify the reflection-transmission spectra into hybrid modes with Rabi splitting of 105 meV.[49]
Based on all these experimental and theoretical studies,the physical picture underlying the strongly coupled atomcavity system has been constructed: The Rabi splitting is the consequence of the cycling interaction of a single photon emitted from an atom with the atom itself, where the frequency of the emitted photon is exactly matching the resonance frequency of nanocavity.Such a process can be well described by the dressed state physics in the standard framework of quantum optics. This physical model not only predicts the existence of Rabi splitting as the intrinsic atom (electron) energy level splitting and extrinsic spectral splitting, but also yields the quantity of spectral splitting in relation with some parameters of the strongly coupled system.[50]However, there remains another equally important issue that is relatively rarely addressed: What is the lineshape of the Rabi splitting spectrum and what influence and determine critical parameters of this lineshape? On the one hand, the traditional models in quantum optics only give the explanation of the energy level splitting in Rabi splitting,[11,50]but rarely discuss how the energy level splitting in Rabi splitting is reflected in the macroscopic optical spectrum. On the other hand, although there is also a small number of references discussing the process of splitting from microscopic level energy to macroscopic optical spectrum,they usually solve this problem by using a statistical method(density matrix method),[51]which is relatively complicated and unfriendly to general readers.
In this paper, we will take this issue by introducing a probing light to detect the strongly coupled photon-atom system and observing the optical spectrum exhibiting Rabi splitting. We will use the hybrid quantum-mechanical model where the interaction of the cavity-mode single photon with atomic states is described by a full quantum mechanical theory and the interaction of the external probe light with the strongly coupled photon-atom system is described by a semi-classical theory. Compared with the existing methods, our model is based on the perturbation theory of the time-dependent Schr¨odinger equation, which can be easily understood by scholars who just study elementary quantum mechanics. This methodology can be used for the intuitive establishment of a physical picture more essentially via only implementing the most concise mathematics.
2. Model and preliminary concepts
We consider some certain amount of two-level atoms placed in an optical cavity.These atoms can jump from ground state|g〉to excited state|e〉via some way of excitation,e.g.,via direct absorption of a photon or via indirect fluorescence process. They can also inversely transit from excited state to ground state by spontaneously emitting a photon or via other non-radiative routes (which are atomic dissipation channels).A spontaneous emission photon has its frequency exactly resonant with the atom transition level. This photon can then be bounced back by the cavity and reabsorbed by the atom, inducing its up-transition from ground state to excited state and igniting the emission-absorption cycling process. Of course,there always exist other photon dissipation channels such as cavity leakage due to imperfect cavity wall reflection and random scattering due to cavity structure irregularities,that compete and hinder the reabsorption of the photon. The emissionabsorption cycling process can happen for some certain times,and the exact cycling number strongly depends on the strength of both atom dissipation and the photon dissipation,which are described by the cavity loss rateκand emitter scattering rateγ,respectively. On the other hand,the cycling number,together with the modal volume of cavity photon (inversely proportional to the optical energy density), will determine the optical field intensity within the cavity and determine the photonatom interaction strength, which is described by the coupling coefficientg.
It has been well established that when coupling coefficientgof the interaction between atom and photon is much larger than cavity loss rateκand emitter scattering rateγ,namely,g ≫κ,γ,the cavity photon-atom system will go into the strong coupling regime, where one can find many interesting quantum phenomena that are absent in weak coupling region (g<κ,γ). This regime is an ingenious method to observe some well-known quantum effects and verify quantum theory. One of the famous instances is Rabi splitting,the splitting of energy levels of an atom surrounded by photon,which is a typical full quantum effect predicted in quantum electrodynamics.
Rabi splitting has been extensively analyzed theoretically and widely observed experimentally. In theory,Rabi splitting can be obtained through an analysis which clearly deduces energy level splitting and anti-crossing phenomenon. In experiment, observers use a probing light to illuminate the cavity consisting of the coupling system between atoms and photon radiated by itself in order to explore the Rabi splitting in photoluminescence, reflection, transmission, or absorption spectra.Note that there are three objects in this process: atoms embedded in the medium and lattice, photon radiated by atoms,and the probing light. The theory about dressed states is associated with the process involving the first two objects, and truly yields the intrinsic cause of splitting.However,observers need the third object to survey the splitting. Currently, there still lacks of a set of appropriate theories to bridge the production from intrinsic microscopic physical mechanism to extrinsically observed spectra. In this paper,we supplement the blank of this theory and deduce the spectral function in the photoluminescence spectra, the double Lorentzian lineshape,from the Schr¨odinger equation, with an ultimate aim to construct a complete quantum theory covering the whole intrinsic and extrinsic chain of this strongly coupling microscopic system. This work provides guidance for the observation of experiment, gives a precise formula of the spectral lineshape and linewidth,and depicts a clear physical picture from a single spectral line to the double spectral lines. It will also lay a theoretical foundation for the study of other influencing factors caused by Rabi splitting such as classical electromagnetic effect.
In this section,we will introduce our model with special emphasis on the role of probing light in observing the Rabi splitting, which aims to study analytically and clearly the relationship between the detection method and the spectral lines that appear when observing Rabi splitting.By the way,we will list the results currently available,and their derivations can be found in most quantum optics textbooks.[11]These results will be used in the process of solution of our model in the next section.
Figure 1 illustrates the model for detection of the system of interaction between atoms and photon. We discuss the single-photon effect here. Note that it is a probing light denoted byEincident externally upon the cavity,as opposed to the photon radiated by atom, that we use to detect the atomphoton system. Thus,we suppose the atoms are immersed in the space full of electromagnetic waveE, which is the tool used to detect the quantum effects (specially, Rabi splitting)occurring inside atoms. The atoms couple with the photon emitted by itself, and the atom-photon coupled system becomes the object under detection and analysis by the background electromagnetic waveE. In this system, we still approximately model the atoms as two-level atoms,as indicated by two horizontal straight lines in Fig. 1(a). There is a photon nearby the two-level atom attributed to spontaneous radiation,and the transition energy¯hϖbetween two atomic levels is equal to energy¯hΩof the photon,namely,the system satisfies the no-detuning conditionϖ=Ω.
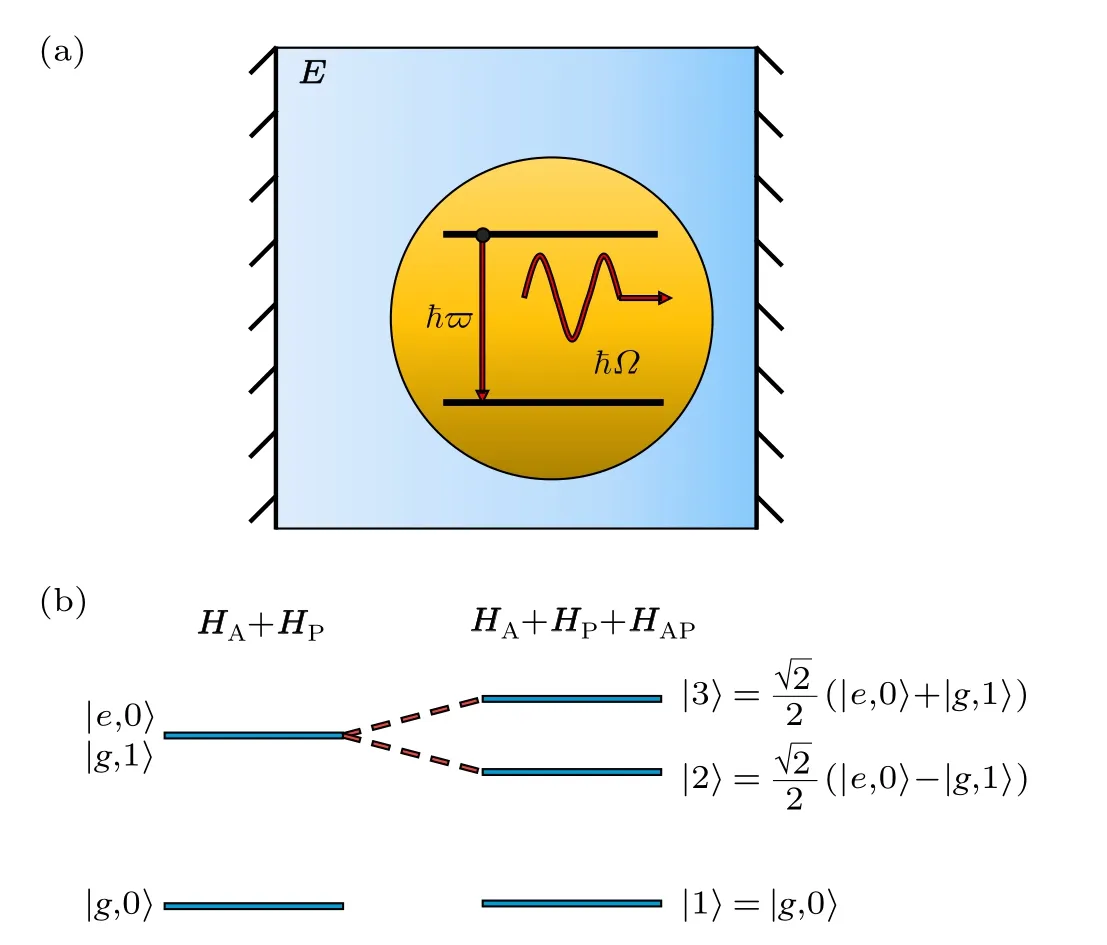
Fig.1. Schematic diagram for the optical spectra observation device for Rabi splitting.(a)An atom-photon system placed in high-Q low mode volume optical cavity exposed to the probing light E. The two-level atom is illustrated by parallel thick black straight lines with transition energy¯hϖ.(b)Schematic diagram for the process of energy level Rabi splitting.The longitudinal direction of the figure denotes the relative magnitude of the energy. If there is no interaction term VAP,the three states of the lowest energy level of the system are shown as the cases on the |g,1〉, |e,0〉 are degenerate. If the interaction term VAP exists, the upper two energy levels will become non-degenerate,which seem to“split”.
In order to reflect the effect of Rabi splitting,we treat the atom-photon system with full-quantum theory, which quantizes both atom and photon states. Therefore,the HamiltonianHof atom-photon system can be expressed as the sum of the Hamiltonian of atomHAand photonHPand their interactionVAP:

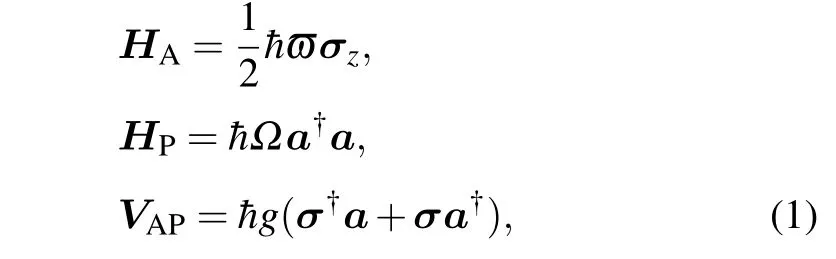
where ¯his reduced Planck constant,ϖandΩare the angular frequencies of two-level atomic transition and photon,σz,σ,andσ†are the Pauli spin operator and spin-flip operators in the atomic vector space,aanda†are the creation and annihilation operators in the photonic vector space,gis the coupling coefficient determined by (here we use bold Italic letters for operators and vectors,thus readers should take care to distinguish them according to the context)

|2〉and|3〉are dressed states which have been proved to be the eigenstates of HamiltonianH. The well-known Rabi splitting is the change from the original degenerate eigenstates (|g,1〉and|e,0〉)of HamiltonianHA+HPto non-degenerate eigenstates(|2〉and|3〉)of HamiltonianH=HA+HP+VAP,as shown in Fig.1(b).|1〉is the common eigenstate of HamiltonianHA+HPandH,because the result is zero when eitherσoracomprised inVAPacts on it.
Given a system where photon¯hΩinteracts with two-level atoms with transition energy¯hϖ,people have to use a beam of probing lightEin order to observe this system. This probing lightEhas rich frequency components so that it can be expressed as

whereElis the complex amplitude of the sinusoidal component at frequencyωl. Note that in order to ensure that the electric field described by the above formula has a physical entity,its value must be a real number,which requires

where the HamiltonianH0describes the atom-photon system in the cavity,and is determined by Eq.(1).μis atomic dipole moment operator.
Under no-detuning conditionΩ=ϖand single-photon condition, all basic eigenvalues and eigenstates (¯hϖiand|i〉fori=1,2,3)of Eq.(6)have been solved in Eqs.(4)and(5).Now, let us solve the wave function of the evolution of this system in term of Schr¨odinger equation and the corresponding initial condition
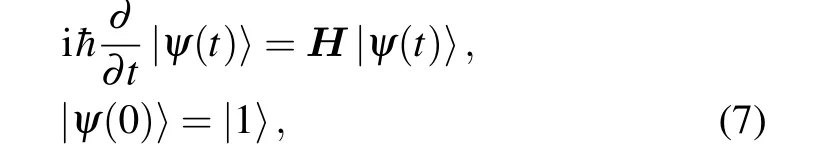
which can help one to get the average polarization and further get the permittivity of the total system. The initial condition indicates the system is located at the ground state initially. We can solve this equation mainly in four steps. First enter the interaction picture,so that we can grasp the essence of the evolution caused by the effect of the probing light. Second,choose a representation to concretize the equation. We use theH0representation. Third, the equations are still difficult to solve directly,and we use the time-dependent perturbation theory to solve them. Finally, use the solution to calculate some average value of the related optical quantities, which can be used to explain and predict experimental physical phenomena. The solution is able to expound the experimental phenomenon of observing the Rabi splitting.
3. Calculation and analysis
In this section, we embark on the calculation of Eq. (7)from which the physical quantity of optical phenomena can be extracted, such as polarization and permittivity. We will get the double Lorentzian lines for the permittivity of the atomphoton system in optical cavity as opposed to classical single Lorentzian line for pure atom systems. We will solve Eq.(7)mainly in four steps.
Firstly,enter the interaction picture. The interaction termVin Eq.(6)is given in Schr¨odinger picture. In the interaction picture,this term becomes

As an example,we calculateμ31andμ32. The others can be found by the same method. Note that〈e|μ|g〉=〈g|μ|e〉=μand〈e|μ|e〉=〈g|μ|g〉= 0 because of the symmetry of the atom as mentioned in Eq.(2).

The first line is the definition of the matrix element. The second line has used the dressed state in Eq. (4). The third line has used the multiplicative distribution law. The fourth line has used the definition of direct product state and⊗denotes the Kronecker product. The last line has used the symmetry of atom and the orthonormality of Fock states. Similarly, we have

The others can be brought out in a similar way. Substituting Eqs. (12) and (5) into Eq. (11) to eliminateμjkandϖj, and figuring out the equations in details,we have


wherecj(j=1,2,3)denote the integral constants determined by the initial condition, such asc1=0. In principle,c2andc3should be computed with the initial condition, but what this article wants to solve is the optical parameters against the steady-state response, not the instantaneous response. Note that terms with integral constant follow an exponential damping factor of time,which tends to zero in a short enough time prior to experimental observation. For example, the damping factorγgrapheneof the atom of graphene is about 1013s-1,whereupon the exponential term will vanish in 30 picoseconds approximately. This time is much shorter than the time for the construction of the system of observation. Thus, we can ignore the exponential terms,that is,we have

So far, we have completed the solution of the wave function in quantum mechanics. We only retain the first-order perturbation here. If the second-order perturbation is calculated,the coefficients of the nonlinear effects such as the second-order susceptibility will be obtained.
The final step is to use the wave function obtained in Eqs. (16) and (17) to bring out the permittivity. According to the rules of quantum mechanics and electrodynamics, the expectation value of the polarization is given by

where
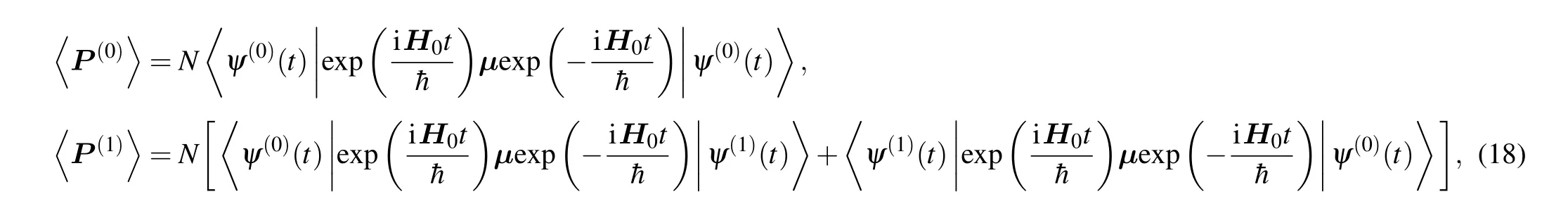
In order to align the picture and the atomic dipole moment operator is in the Schr¨odinger picture, we manifest the exponential multiples in Eq.(18)to transform the wave function|ψI(t)〉in the interaction picture into the wave function|ψ(t)〉in Schr¨odinger picture too. Substituting Eq. (17) into Eq. (18), we get the zero-order perturbation polarization〈P(0)〉=0 and the first-order perturbation polarization

where we have considered that the frequency of the probing light is continuous and thus we have replaced the symbolωlwith common symbolω.
The relative permittivityεr(ω)in Eq.(19)presents a double Lorentzian lines with two peaks at frequencyω=ϖ±g,as shown in Fig. 2(a). In other words, the difference in frequency between the two peaks is 2g. Moreover,the line width of each Lorentzian line is related to damping factorγ2orγ3.The larger the damping factor,the wider the line width. Thus,this theory well explains why it is necessary to reach the strong coupling regime in order to observe the Rabi splitting. One of the conditions for realizing the strong coupling is the coupling coefficientgis much larger than the damping factor, namely,g ≫γ2,γ3. If the coupling coefficientgis too small, the two peaks are too close to be identified and emerge together, as shown in Fig.2(b).Only when the coupling coefficient is large enough,the two peaks corresponding to the Rabi splitting will distinctly appear in the spectrum. Note that the spectrum belongs to probing light rather than the atom-emitting photon in our atom-photon system, because the frequency of photonΩirradiated by atom in the cavity is constant(Ω=ϖin our model under no-detuning condition), in contrast to the variable frequency of probing lightωrunning over a wide spectral range in practical experiments.
In recent years,many research results have focused on the distinction between mode splitting(Rabi splitting)and electromagnetically induced transparency (EIT). Rabi splitting and EIT are indeed very similar in phenomenon,both are reflected in the appearance of two peaks in the spectrum, but they are quite different in physical essence. Our model and result can clearly distinguish these two phenomena. In term of the physical origin,Rabi splitting requires only two-level atoms to produce, while EIT requires three-level atoms. In term of the physical experimental result, the Rabi splitting is a double Lorentzian lineshape as described by Eq.(19), while the RIT is a cubic polynomial lineshape as described by Eq. (7.3.15)in Ref.[11]. Thus,they can be distinguished by fitting experimental data of the spectral profile. In this regard,our concise model is also helpful to differentiate the mode splitting and EIT.

Fig. 2. Schematic diagram for the double Lorentzian line described by Eq.(19).The abscissa and vertical coordinate indicates the angular frequency of the probing light and the imaginary part of the relative permittivity for the entire system H. (a)Some parameters meaning in Eq.(19),which show two peaks at ω =ϖ-g and ω =ϖ+g, respectively, with line width of γ2 and γ3. (b)Two peaks changed by coupling coefficient g. The upper g is small,and the lower g is large. Only when g is large enough will there be obvious double peaks. Otherwise the double peaks will disappear.
Our model and results establish a bridge from microscopic quantum phenomena to macroscopic optical observations. There is an atom (or an emitter), which is easily disturbed by the outside world and radiate photon. Then atom and this photon form a system and couple together under the strong confinement of the optical cavity,which exhibits colorful microscopic quantum phenomena,such as Rabi oscillation and Rabi splitting. In order to observe and analyze the atomphoton system,people often place this system in a high-Qlow modal volume resonant optical micro/nanocavity and illuminate it with probing light. The probing light can interact with the entire system,carry out part of the information of the system and present it extrinsically in the form of optical spectrum.The macroscopic spectrum can reflect many microscopic characteristics,such as the density of microscopic particle,atomic dipole moment, the interaction or coupling strength, the construction of energy level, the damping of system, which can be found from Eq.(19). This is an intuitive clue from microscopic to macroscopic world.
To go further, our results also link macroscopic electromagnetism with microscopic quantum mechanics. So far,the macroscopic limits of quantum mechanics have yet to be discussed. How tiny an entity must be when it must be described by microscopic quantum mechanics instead of macroscopic electromagnetism? A thousand of atoms? One million of atoms? Besides, is there a continuous transition between microscopic quantum mechanics and macroscopic electromagnetism? The above question involves the connection between macroscopic world and microscopic world. Our model gives an example of fusion of electromagnetics and quantum mechanics. The relative permittivity and polarization are characteristics derived from macroscopic electromagnetics,which contain the information about the interaction between light and matter. Based on immutable Maxwell equations, the diversity in the permittivity of matter manifests many colorful macroscopic optical phenomena, whether well known or still unknown. The atomic dipole moment introduced in Eq.(2)is the characteristic derived from microscopic quantum mechanics. It plays a significant role in the interaction between light and matter, which is the intensity coefficient that determines the coupling term between photon and atom. Here, we link the two physical quantities in Eq. (19), which is in different word but both describe the intensity and tightness of the coupling effect between light and matter.
4. Conclusion
In summary,we have built up a model physical system to describe the process of detecting Rabi splitting of a stronglycoupled atom-photon system in the platform of high-Qlow modal volume optical micro/nanocavity via an external probing light. We have constructed a quantum theory that can describe the optical response of the strongly-coupled system under the action of the external probing light and the corresponding spectral lineshape. We have taken the Hamiltonian for the strongly-coupled photon-atom system as the unperturbed HamiltonianH0and the interaction Hamiltonian of the probing light upon the coupled-system quantum states as the perturbed HamiltonianV. Based on the dressed state basic quantum states,which are the eigenstates ofH0,we can solve the evolution of these quantum states under the action of the probing light as described byV. Then all the relevant quantities such as the atomic dipole moments, the effective permittivity, the optical response, and spectral lineshape of the strongly-coupled photon-atom system can be solved in the standard framework of quantum mechanics. The theory shows that the strongly-coupled system exhibits a double Lorentzian lineshape, which agrees well with experimental observation of Rabi splitting in the form of spectral splitting. Moreover,several critical parameters such as spectral strength, spectral splitting,and spectral linewidth can be related to the intrinsic parameters of the strongly-coupled atom-photon system.
Our theory offers a good theoretical platform to understand the macroscopic optical properties for the strongly coupled system composed of atoms, molecules, molecule aggregates, and semiconductor quantum dots embedded within an optical microcavity/nanocavity with high quality factor and/or low modal volume, in particular, the prominent quantum effect of Rabi splitting due to the strong coupling of cavity-mode single-photon with the two-level atomic states. Moreover,this theory can also serve as a useful theoretical tool to construct a bridge between the microscopic atomic energy level splitting and the macroscopic optical spectral splitting, and see whether or not these two quantities exactly have the same values. On the other hand, readers can use the permittivity presented for the first time in this article as a starting point to solve the transmission or reflection spectrum in optical cavity involving strongly-coupled atom-photon systems and help to discover fine new physical phenomena and new physical laws. Finally, our theory can inspire people to, explore more deeply the connection between the macroscopic world and microscopic world,visit new physical phenomena and laws in the mesoscopic world,and deepen our understanding of the physical world at different levels.
Acknowledgments
Project supported by the National Key Research and Development Program of China(Grant No.2018YFA0306200),the National Natural Science Foundation of China (Grant No.11974119),and Guangdong Provincial Innovative and Entrepreneurial Research Team Program,China.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Helium bubble formation and evolution in NiMo-Y2O3 alloy under He ion irradiation
- Dynamics and intermittent stochastic stabilization of a rumor spreading model with guidance mechanism in heterogeneous network
- Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
- Low-overhead fault-tolerant error correction scheme based on quantum stabilizer codes
- Transmembrane transport of multicomponent liposome-nanoparticles into giant vesicles
- Molecular dynamics simulations of A-DNA in bivalent metal ions salt solution
