框架结构中楼梯抗侧刚度的影响因素及计算方法研究
2023-03-13程远兵
常 青 程远兵
(华北水利水电大学土木与交通学院,河南 郑州 450045)
0 引言
楼梯作为房屋建筑中必不可少的组成部分,是紧急状况下重要的疏散和逃生通道。由于楼梯间的构造不同于楼层的其他部分,导致其受力复杂,在发生地震时,容易先于主体结构发生破坏[1]。为保证楼梯在紧急状况下起到“安全岛”的作用,做好楼梯间的抗震设计尤为重要。汶川地震之前,在我国的建筑抗震设计中,将楼梯构件看作仅承受竖向荷载的受弯构件,不考虑楼梯对结构抗侧刚度的影响[2],忽略了楼梯对结构的斜撑作用,导致结构抗震计算不合理[3-4]。大量的震害调查表明,楼梯在地震中损毁严重,主要表现为梯段板断裂、梯梁扭断、框架短柱破坏等[5-6]。目前,通用的设计软件为有限元分析方法,在结构抗震计算中计入了楼梯结构的抗震影响,但是缺乏楼梯抗侧刚度的计算。综上所述,由于框架结构是最常用的结构型式之一,对框架结构楼梯间的抗震性能研究迫在眉睫。
近年来,国内外的研究人员对楼梯的震害特征进行了分析,研究了楼梯间位置、支座布置等因素对整体框架结构刚度的影响。常亚峰等[7]利用ETABS对包括和不包括隔震防倒塌支座的框架结构计算模型进行分析,结果表明设置隔震防倒塌支座可保证楼梯的整体稳定性。Faizan等[8]研究了建筑高度变化、楼梯平面布置及楼梯间的填充墙对建筑的影响。王建强等[9]对有无楼梯的框架结构进行地震反应分析,结果表明楼梯与整体结构共同工作时,楼梯构件的内力显著增大且受力状态复杂。敬艳梅等[10]通过对现浇板式楼梯框架模型进行弹塑性分析,得出模型的失效是从楼梯发展到框架,由下层发展到上层的结论,并针对模型的失效机制特点提出了相应的抗震措施。
为解决楼梯构件抗侧刚度的计算问题,本研究以楼梯间的层高h和开间宽度b为基本参数,将混凝土强度等级、楼梯构件截面尺寸等参数取为固定值,对框架结构楼梯间进行有限元分析。对分析得出的数据进行拟合,回归出框架结构楼梯的抗侧刚度计算公式。
1 有限元模型的建立
1.1 参数选取
ANSYS软件是一个常用的有限元软件,可以灵活地对结构进行分析。其可任意设定荷载工况,实现对结构的整体分析。同时也可以对细部加密网格,得出较为精确的细部结果。
为了避免因单元细分而导致的应力奇异问题,提高整体计算的收敛性,采用整体式建模。在有限元模型里,通过把钢筋“弥散”于整个单元中的方法,将钢筋混凝土材料视作单一材料。
梁、柱选用BEAM188单元,即3D线性有限应变梁,主要用于模拟考虑剪切变形影响的细长到中等粗短的梁结构。该单元有两个节点,每个节点有6、7个自由度,即3个平动自由度Ux、U y、Uz和3个转动自由度Rotx、Roty、Rotz,同时支持约束扭转,通过激活第七个自由度warp使用。该单元非常适合用于分析线性、大角度转动和非线性大应变问题。
板选用SHELL181单元,即有限应变壳,主要用于模拟薄壳至中等厚度壳结构。该单元有4个节点,每个节点有6个自由度,即沿x、y、z方向的平动位移和绕节点x、y、z轴的转动。该单元有强大的非线性功能,并具有截面数据定义、分析、可视化等功能,还能定义复合材料多层壳。
1.2 模型的建立
根据《建筑设计防火规范》(GB 50016—2014)和《高层民用建筑设计防火规范》(GB 50045—95)的有关规定,楼梯平台的宽度不应小于梯段板的宽度,因此本模型楼梯平台的宽度等于梯段板的宽度。楼梯间整体模型只取层高h和开间b这两个参数作为影响因素。其余各个参数,结合实际工程的常见情况,取为固定值,分别为:框架柱截面为400 mm×400 mm;框架梁截面为250 mm×600 mm;楼梯柱截面为250 mm×250 mm;平台梁截面为250 mm×400 mm;楼梯梯段板厚120 mm,踏步宽为280 mm、高为150 mm;休息平台板厚均为100 mm;楼梯井宽为150 mm;楼梯构件混凝土强度等级均为C30。模型参数如图1所示。
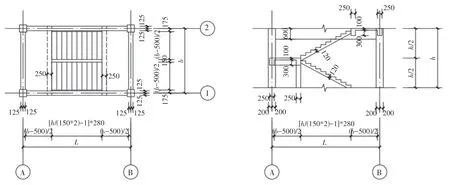
图1 楼梯间整体模型参数(单位:mm)
因楼梯间整体模型只取层高h和开间b作为变化参数,所以进深如式(1)所示。
根据式(1),对楼梯间的层高h和开间b进行变化,建立如图2所示的整体模型。
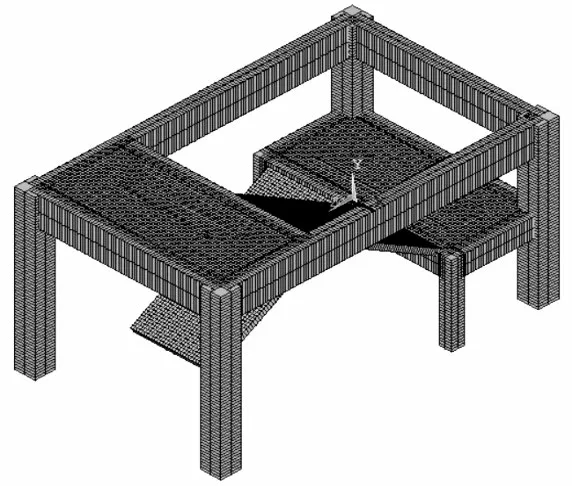
图2 楼梯间整体模型
2 楼梯的抗侧刚度
2.1 楼梯抗侧刚度的确定
具体步骤为:一是采用有限元分析,得出楼梯间整体模型的抗侧刚度(通过对楼梯间顶部施加单位位移的方法);二是采用有限元分析,得出框架柱的刚度(通过对柱顶部施加单位位移的方法);三是将步骤一和步骤二得出的结果相减,即为楼梯结构的侧向刚度。
2.2 楼梯抗侧刚度的变化规律
先保持楼梯间开间宽度b不变,变化层高h,分别取层高h为2.7 m、3.0 m、3.3 m、3.6 m、3.9 m、4.2 m、4.5 m、4.8 m;再保持楼梯间层高h不变,变化开间宽度b,分别取开间宽度b为2.7 m、3.0 m、3.3 m、3.6 m、3.9 m、4.2 m、4.5 m,4.8 m。根据相关数据和图1计算出其他参数,逐个建出楼梯间整体的有限元模型。依次对模型进行有限元分析,得到每个模型中的楼梯抗侧刚度如表1所示。
根据表1的结果,绘制出楼梯抗侧刚度与层高的关系如图3所示,绘制出楼梯抗侧刚度与开间宽度的关系如图4所示。
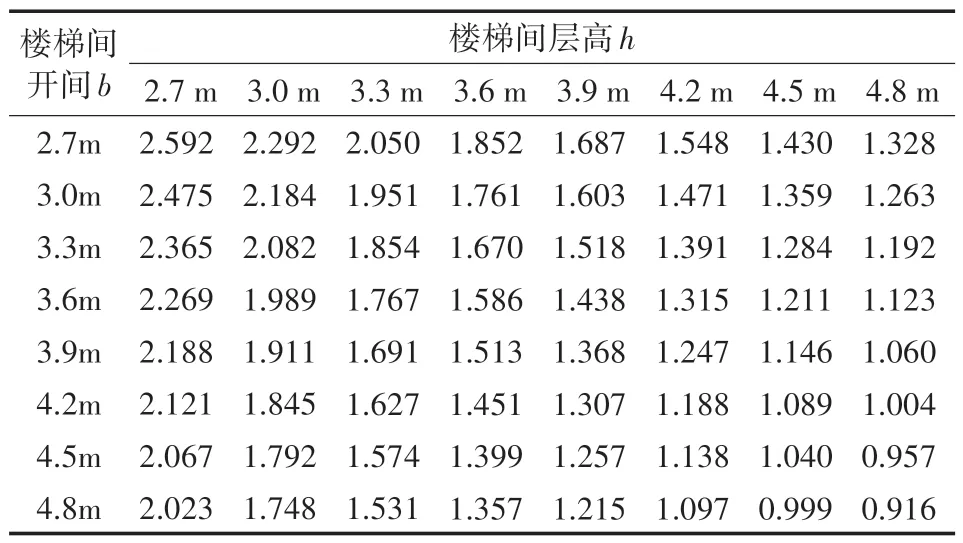
表1 楼梯抗侧刚度的有限元分析结果单位:108 N/m
从图3和图4可以看出,当楼梯间开间宽度b不变时,楼梯的抗侧刚度随楼梯间层高h的增大而减小;当楼梯间层高h不变时,楼梯的抗侧刚度随楼梯间开间b的增大而减小。
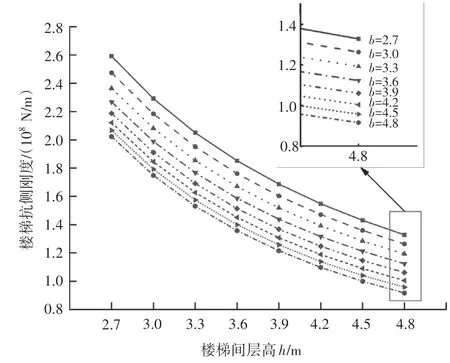
图3 楼梯抗侧刚度与楼梯间层高的关系
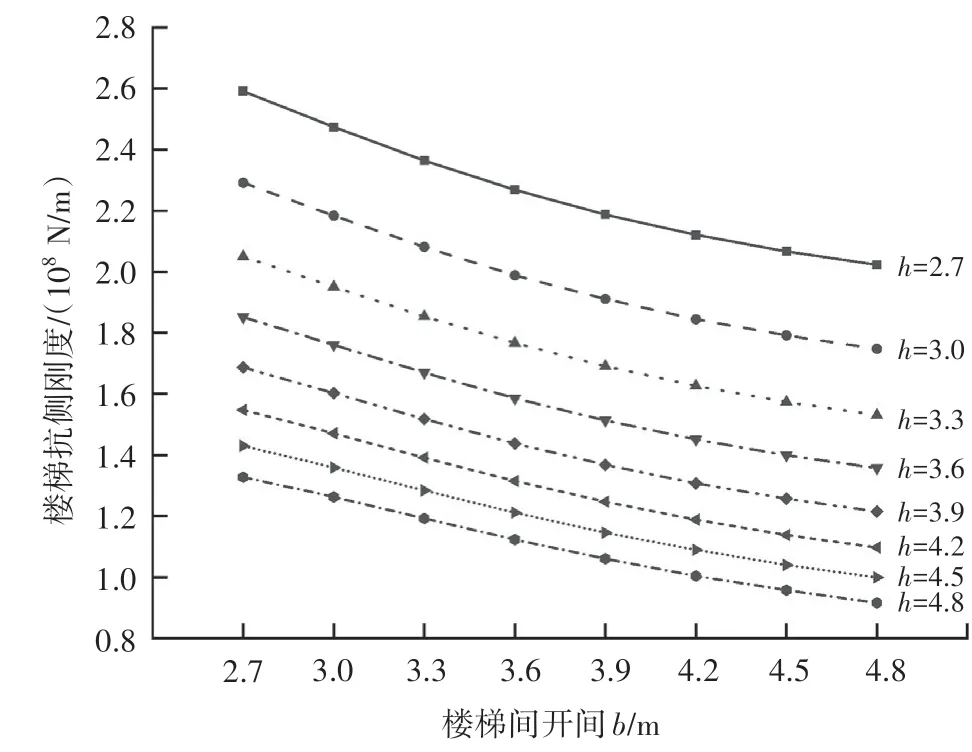
图4 楼梯抗侧刚度与楼梯间开间宽度的关系
2.3 楼梯抗侧刚度的计算公式
2.3.1 楼梯抗侧刚度随层高h变化的公式。当楼梯间开间宽度b不变时,使用Eureqa软件对有限元分析得到的数据进行拟合,得出楼梯的抗侧刚度随楼梯间层高h变化的计算公式,公式及误差见表2,表中k的单位为108N/m。
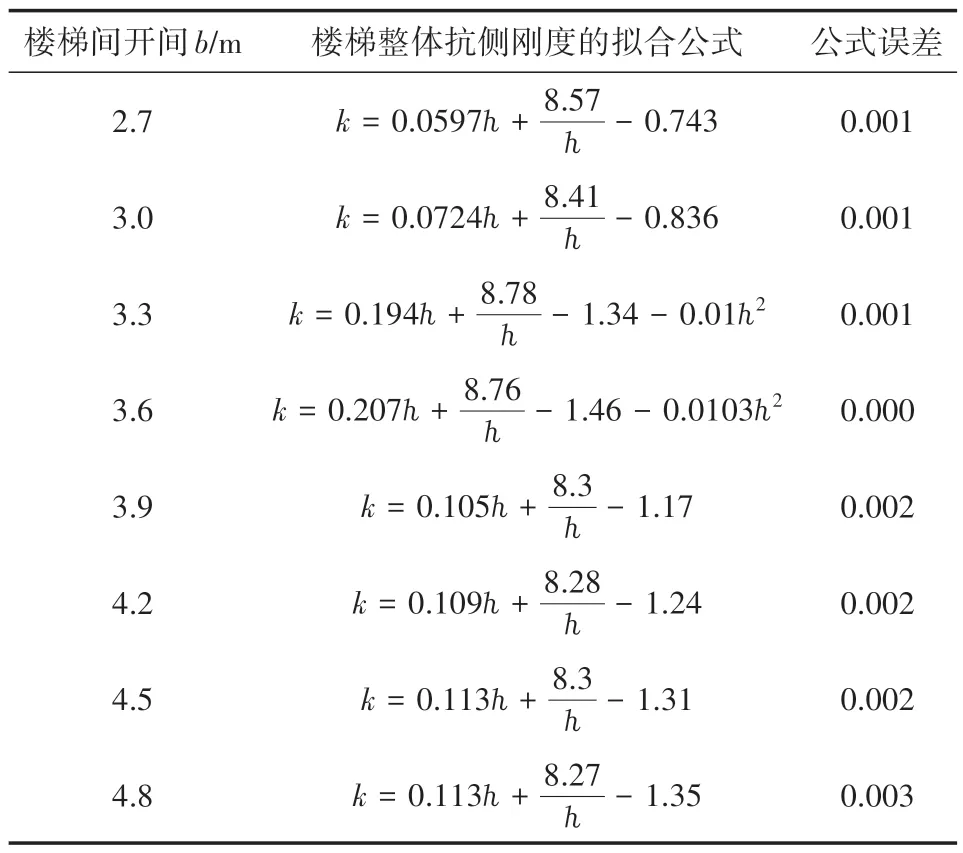
表2 楼梯整体抗侧刚度的拟合公式
2.3.2 楼梯抗侧刚度随开间宽度b变化的公式。当楼梯间层高h不变时,使用Eureqa软件对有限元分析得到的数据进行拟合,得出楼梯的抗侧刚度随楼梯间开间宽度b变化的计算公式,公式及误差见表3,表中k的单位为108N/m。
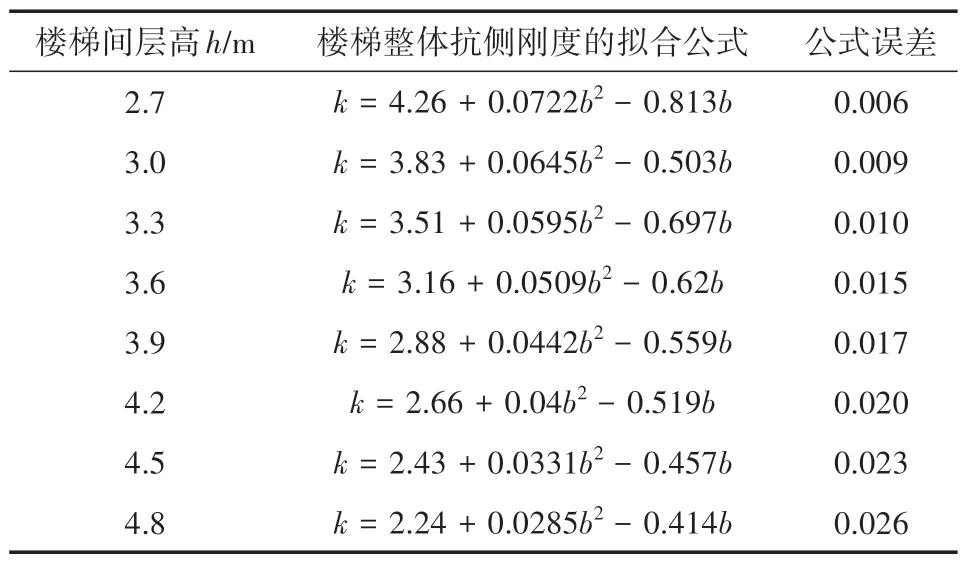
表3 楼梯整体抗侧刚度的拟合公式
2.3.3 楼梯抗侧刚度随层高h和开间宽度b变化的公式。当楼梯间层高h和开间宽度b同时变化时,使用Eureqa软件对有限元分析得到的数据进行拟合,得出楼梯的抗侧刚度随楼梯间层高h和开间宽度b变化的计算公式,公式及误差见表4,表中k的单位为108N/m。

表4 楼梯整体抗侧刚度的拟合公式
3 结语
以框架结构的楼梯间作为研究对象,选取楼梯间的开间、进深和层高等作为影响因素,采用有限元分析的方法,建立了分析模型,变化相关参数,通过对楼梯间施加层间侧移,并对相关数据进行分析,得出如下结论。
①当楼梯间的开间宽度b不变时,减小楼梯间的层高h可以增大楼梯的抗侧刚度。
②当楼梯间的层高h不变时,减小楼梯间的开间宽度b可以增大楼梯的抗侧刚度。
③利用ANSYS软件对楼梯间进行整体建模分析,根据得出的数据,通过Eureqa软件进行拟合,回归出了楼梯抗侧刚度在不同影响因素下的计算公式,可为框架结构中楼梯参与结构整体抗震设计时提供参考。
