基于SIR 模型的航班延误扩散行为研究

王亚含，姚红光 WANG Yahan,YAO Hongguang

（上海工程技术大学 航空运输学院，上海 201620）

0 引言

近年来，航班计划在稳步调整，航班运行量也在稳步增加，但不可避免的航班延误扩散现象一直为航空运输带来了许多负面影响，如旅客的不满、航空公司成本的损失、航空公司的服务满意度受到影响等。2017 年至2020 年全国客运航班公司平均航班正常率稳步增长，但延误航班的数量却在增加[1]。因此，对航班延误扩散传播行为的趋势变化进一步分析有利于掌握其客观规律，对其研究可以为有关部门在缓解航班延误扩散问题上提供决策依据。

刘玉洁等人[2]建立的延误波及模型是分析同一航班链下的航班延误波及情况，基于贝叶斯网络从微观的纵向航班链角度来讨论延误波及的有关问题。丁建立等人[3]结合有色Petri 网和时间Petri 网双理论，对延误航班间的关联逻辑关系建立航班延误链式反应关系模型—有色-时间Petri 网，通过仿真实验得出，延误时间越长，影响到下游航班个数越多。Wu 等人[4]考察延误传播效应使用了Copula 函数，对缓冲时间进行变量，结果表明增加缓冲时间，可降低延误航班对下游航班的影响。邵荃等人[5]考虑到复杂网络的拓扑结构建立了有权有向的网络模型，对某省会机场进行延误横向、纵向波及效应的分析。Nakata 等人[6]应用传染病传播理论分析了运输网络下网络拓扑连接性的不同与传播程度的关系。

近年来传播动力学理论也被逐渐用于空中交通延误相关研究中，其中部分学者建立传播动力学模型对航班延误扩散展开研究。武喜萍等人[7]以宏观角度分析航空交通延误传播与负荷容量级联失效模型之间的相似性，并把此模型和SIS 模型进行结合改进建立了空中交通延误传播SIS 模型，最后通过实例验证了改进模型的有效性。王兴隆等人[8]从宏观机场节点角度出发，考虑到机场网络下延误传播具有时变性，以机场为节点，构建了时变机场网络延误传播模型，根据其网络延误传播过程里机场节点不同状态之间的转变机理，来进行模型仿真并进行实验参数分析。Li Shanmei 等人[9]基于平均航班延误波动，从网络层面建立了数据驱动模型下的易感-感染-康复-易感传播模型，对其进行相轨迹分析，更好地了解机场网络下延误波动演化的过程，并通过仿真来模拟模型下机场网络间的延误传播。张兆宁等人[10]为了能够更好的应对航班延误大面积扩散问题，在空中交通网络环境下基于SEIR 模型相关理论，建立了航班延误传播模型，通过分析节点状态变化计算基本再生数来分析预测大面积航班在机场间发生延误传播的过程变化情况。代晓旭等人[11]建立空中交通拥挤传播SIR 模型，分析拥挤传播影响因子和消散因子对延误传播的影响，在结合实例过程中发现若空中交通拥挤情况较复杂时，新的参数情况则需考虑进来。王晶华等人[12]针对大面积航班延误传播问题，基于航班状态转化，构建SIR 传播模型，并对延误传播参数和消散参数进行分析讨论，来探索大范围面积的航班延误传播的动态过程和变化规律。

现通过分析SIR 模型与延误扩散之间的相似性，将传统SIR 模型与航班延误扩散行为结合起来，建立航班延误扩散SIR 传播模型，通过比较不同数值下相轨线的变化来分析正常状态航班和已延误并有扩散能力的航班二者变化关系，改变参数变化，以此更好地理解航班延误扩散的演化趋势。

1 航班延误扩散机理及SIR 模型

1.1 航班延误扩散机理

一般情况下，航班晚于计划的15 分钟起飞或到达时，即视为航班起飞或到达延误。据民航局统计，近年来因天气等一些不可抗力的延误因素引起的航班延误一直以来占较大的比例。而一旦发生航班延误现象，由于航班时刻连续性、空间有限性以及机组间相关性等互相作用原因，延误则不可避免的会影响波及到机场及航空公司下游其他航班，航班延误扩散现象往往产生。

如果没有出现航班延误情况整个航班计划将是一个动态平衡的状态。假设出现初始的航班延误时，航班计划的动态平衡状态被打破，鉴于航班运行是由多个部门协同合作完成，资源之间具有共享性，与此同时航班延误扩散不仅会受到多部门间的制约，还会受到其他不同因素的影响，例如，跑道、机场容量、地面设施、每天初始延误航班的数量、航班延误时间、飞机停留所需的服务时间、该航班链下的机场总数、航班总计划量、每条航线中航班数量、航空网络中航线数、空域等这些因素都会影响航班延误的扩散程度。如果延误的航班得不到及时妥善处理，航班计划系统鲁棒性则会下降，在航空网络环境下，延误波及的扩散一开始由初始航班的延误通过网络中节点间的耦合联结作用影响到下游其他原航班的计划，造成“多米诺骨牌”连锁反应，最终会使得整个航班运行系统将会被打破，导致航班延误数量急剧增加，形成航班延误扩散现象。例如图1 中，建立由10 个机场组成的简单航班计划模型，机场下航班间的联系通过航线实现，除始发机场外停留时间均为一小时，可以看出，若其中某个机场的某个航班出现延误，在有限资源相互制约下，可能导致该机场的其他航班无法正常按航班计划运行，产生扩散情况。

图1 航班计划模型示意图

1.2 航班延误扩散SIR 模型分析

传统SIR 模型可分为三类：易感者S，t 时刻内未染病但有可能被该类疾病传染的人数比例则记为S（t）；染病者I，t 时刻内已被感染成为病人而且具有传染力的人数比例则记为I（t）；移出者R，t 时刻内已从染病者中移出的人数比例则记为R（t）。而航空网络下航班延误扩散属于时空传播动力学范围，所以上述的传播机制在航班延误扩散中也存在。

把SIR 传播动力学模型传播过程按其内在规律类比到航班延误扩散过程中也具有一定的相似特征，可以发现：

（1）上游延误航班将延误传播到与之相连的下游其他航班；这就相当于已延误并有扩散能力的航班I 可将延误扩散到其他相关联的正常状态航班S。

（2）延误的航班不会对正在完成飞行任务的航班有影响，其延误扩散的连锁反应仅存在于待完成航班中。

（3）延误航班若能妥善控制延误扩散所造成的风险，则该航班不会受延误扩散的影响；这就相当于待完成该次飞行任务的航班R 已不受航班延误扩散行为的影响。

所以航班延误扩散SIR 模型下的三种类型状态，即机场下正常状态航班S，指发生延误时，还未受到延误扩散的影响，其随时刻t 的比例变化记为S（t）；机场下已延误并有扩散能力的航班I，且具有的扩散能力还可能影响与之相关联的后续航班,其随时刻t 的比例变化记为I（t）；机场下已恢复正常状态的航班R，指能控制住延误扩散所造成的风险，不受延误扩散的二次影响，其随时刻t 的比例变化记为R（t）。

由以上分析可知，这两种传播过程所涉及到的类型状态、传播行为都具有一定程度的相似性，在理论上一定程度的论述了借鉴传播动力学模型的基本思想来研究航班延误扩散的合理可行性。

2 航班延误扩散传播模型

对于航班延误扩散SIR 模型，假设一定空域内单位时间内航空网络中运行航线数N 是不变的；不考虑返航、备降和取消航班等其他情况；根据以上说明，基于SIR 的航班延误扩散模型传播机制如图2 所示。

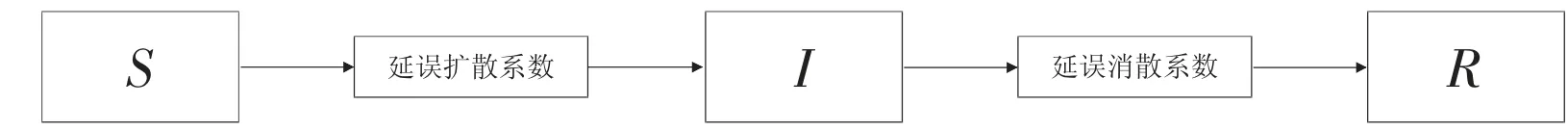
图2 航班延误扩散SIR 模型

为了方便研究，以公式（1）为传播过程中所处状态下随时间变化的密度表达方程组：

在式（1）中，方程组分别表示为t 时刻正常状态下航班所占的比例；t 时刻已延误扩散的航班比例和时刻航班已恢复正常状态时所占比例。α 为延误扩散系数，表示延误扩散航班的传播概率，在实际情况下，航班计划安排、空域容量等因素影响其取值；β 为延误消散系数，表示由延误扩散状态恢复为航班正常状态的概率，在实际情况下，空域容量、机场容量等因素影响其取值；其二者均为正实数，其比值v 表示相对移除率，表达式为：

以上方程组不存在解析解，相对移除率在模型中采用相轨线分析法，对式（1）计算可得S（t）与I（t）间的关系，S-I 相平面上的相轨线方程为：

解得：I+S-vlnS+C=0。

新的函数关系为：f（S,I）=I+S-vilnS+C。

不断地调整参数α，β 和初始值S（0），I（0）的取值，从输出的数据及图形来观察航班延误的传播规律。分别取v=0.6、1、5/3，其相轨线如图3（a）、（b）、（c）、（d）、（e）、（f）所示，相轨线方向全部为逆时针。

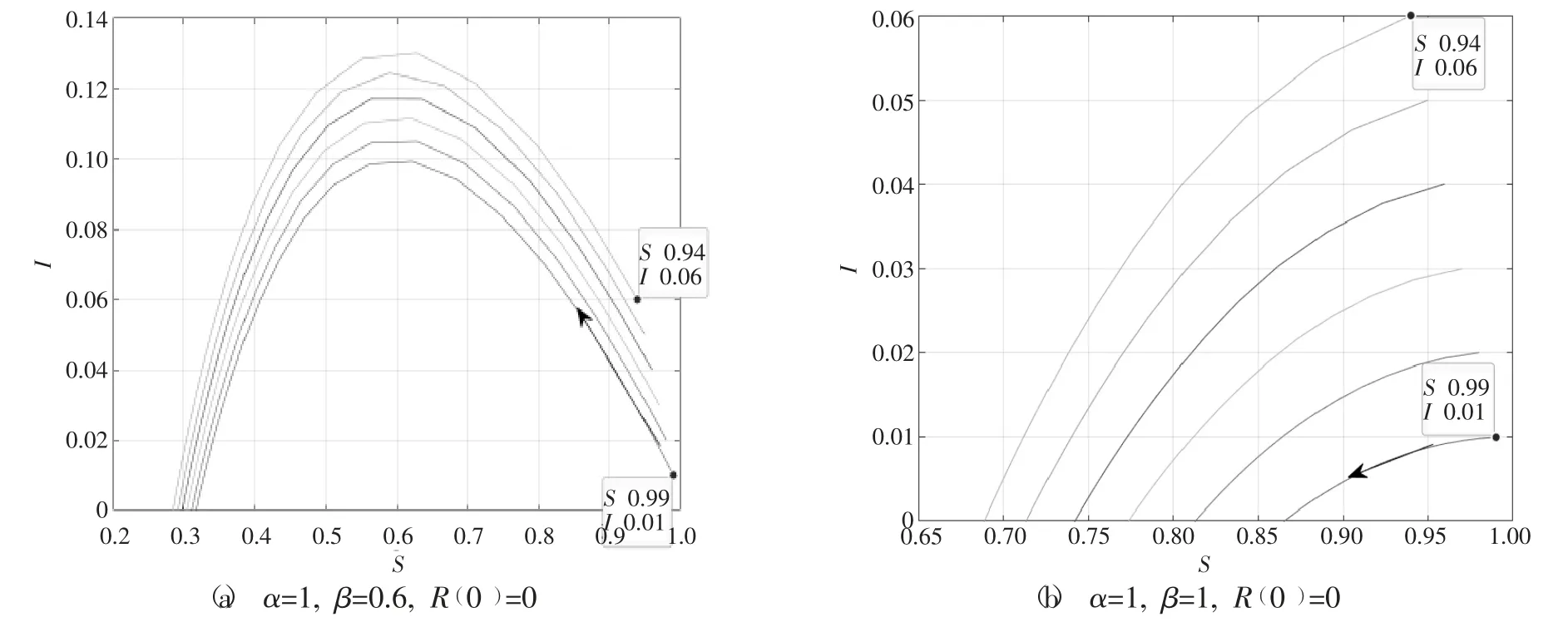
图3

对比以上图形可得，随着改变相对移除率的取值，曲线的峰值也不同，说明了延误扩散反应程度不一。由图3（a）、（d），图3（b）、（e），图3（c）、（f）可知，通过改变初始值S（0），I（0）也可影响到航班延误扩散的行为。进一步的，如果v 的比值小于1 时，S（t）呈现单调下降的趋势，I（t）则呈先上升后下降的变化，表明在此情况下，航班延误扩散行为有蔓延现象，延误航班数量将到达某个峰值，航班延误扩散情况较为严重。反之，如果v 的比值大于1 时，S（t）和I（t）均呈现单调下降的趋势，甚至下降至0，这表明通过减少正常航班节点或增加相对移除率的情况下，航班延误扩散行为将有效得到控制，延误扩散情况得到缓解。由此可以得到以下结论：

（1）当S=v 时，该点所在曲线的位置为最高点位置，I（t）达到峰值，因延误扩散造成航班延误数量此时最多。

（2）当S＜v 时，I（t）值减小，延误扩散状况得到缓解且进入消散阶段。

（3）当S＞v 时，I（t）值增大，延误扩散状况进一步加剧。

3 航班延误扩散模型仿真分析

3.1 延误扩散系数变化下的扩散行为分析

（1）赋予一组初始标准化数据；模型求解方法步骤如下所示：设定各个变量和参数的初始取值，S（0）=0.98，I（0）=0.02，R（0）=0。时间t 为自变量，因变量则为各节点状态的比例。

（2）输入有关参数，参数取值参考文献[11]；把上述数据代入公式（1）。

（3）运行模型；使用Matlab 对建立的数学模型仿真。

（4）分析图形变化。

取β=0.1 保持不变，α 分别取0.15、0.3、0.45、0.6、0.75，观察I（t）和S（t）的变化，如图4（a）、（b）所示。

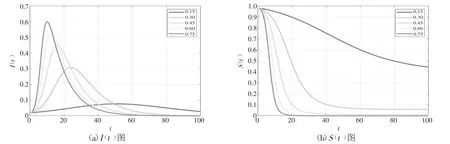
图4

图4（a）中随着时间t 的增加，I（t）曲线变化为先上升后下降；比较五组数据可知，当增大延误扩散系数α，I（t）曲线越陡峭，也更早的达到峰值，且峰值在不断变大，其增长和下降的也更快。图4（b）S（t）中随着时间t 的增加而下降，且当延误扩散系数α 越大，S（t）下降速度越快，最后较早达到平稳状态。以上分析可得，在航班延误传播过程中，已延误并具有扩散能力的航班随时间的增加则先上升后下降，说明延误扩散行为在初期较为严重，到后期逐渐消散。并且系数α 越大，延误的航班敏感度较高，则导致延误扩散传播的现象更严重。所以降低延误扩散率，将有效地缓解航班延误扩散现象。

3.2 延误消散系数变化下的扩散行为分析

取α=0.8 保持不变，β 分别取0.1、0.2、0.3、0.4、0.5，观察I（t）和S（t）的变化，如图5（a）、（b）所示。

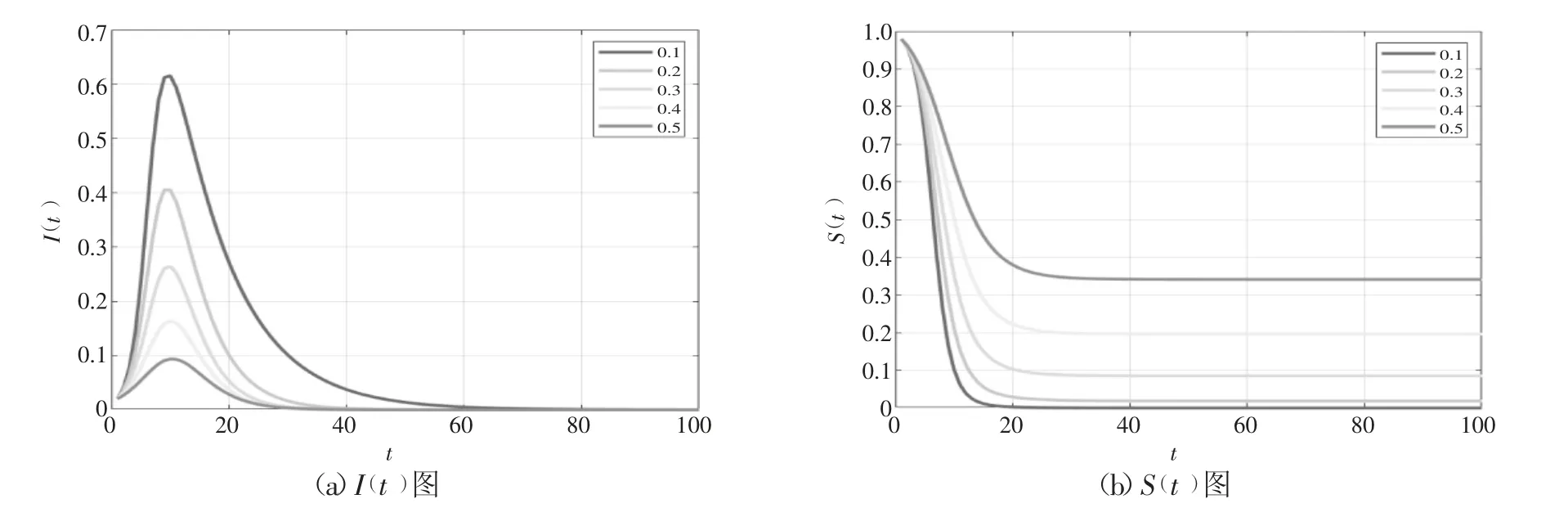
图5

在图5（a）中，比较五组数据可得I（t）曲线的变化趋势随着延误消散系数β 的增大而变得平缓，峰值在不断减小且出现时间较靠前；图5（b）S（t）曲线随着延误消散系数β 的增大其稳定值在升高，达到稳定状态时所需的时间也较长，表明S（t）转换成I（t）的概率在增大。以上分析可得，在航班延误扩散传播过程中，延误消散系数β 越大，延误航班扩散行为消散的越快，即已延误并具有扩散能力的航班比例呈减小趋势，延误传播严重现象得到缓解，最终扩散将会停止。正常状态下的航班也将会达到平衡。

4 结束语

通过分析航班延误扩散行为的传播现象与传染病SIR 模型间的相似性，发现航班延误扩散传播过程与传染病的传播相结合有较大可行性。于是基于SIR 模型的基础上建立了航班延误扩散传播动力学模型，通过对相轨线进行分析比较，讨论相对移除率v 的数值变化与延误扩散行为的关系，研究得出尽可能让S 小于v，来缓解延误扩散行为的严重性；通过对参数进行分析，得出其参数变化对延误及消散的影响。希望在今后的研究中，应积极考虑航班状态间的转变情况，为减少延误扩散现象提出可行措施与意见。