疫情背景下物流企业间极端风险溢出效应研究——以顺丰控股和圆通速递为例

曾从豪（南京林业大学 经济管理学院，江苏 南京 210037）

0 引言

物流概念在国外已有近百年的发展史，日本从美国引用了PD（Physical Distribution）概念，并用日文“物流”代替，我国如今日常使用的“物流”一词，便是从日文翻译而来。

1978 年11 月，原国家物资总局副局长陶立同志率领由17 人组成的中国物资工作考察团前往日本学习生产资料管理和流通情况，并出版和发行了《外国和港澳地区物资管理考察》一书。1979 年10 月，日本物的流通协会副会长十时昌、东京大学教授林周二等人组成的日本物的流通协会物流访华团，在我国北京、上海、成都等多地进行学术讲演，详细介绍了国外物流发展现状以及物流管理经验，在我国引起强烈反响，“物流”一词也因此在国内迅速传播开来。1988 年，我国设立物资部，开展了物资运输的专项行动。1992 年，小平同志在南巡讲话中表示，要建立社会主义市场经济体制、拓展物流外包、提高物流管理水平，引进国外的物流思想、技术和模式，最终达到让中国的物流企业走上正轨的目标。与此同时，民营物流企业也在快速发展，国有物流企业向现代物流企业转变，国有和民营两方形成了新格局。21 世纪初，我国正式加入WTO。随着改革开放进程的加快，现代物流也随之进入了“新纪元”。近15 年来，我国物流业发展极其迅猛，覆盖范围急剧扩大，包括了以顺丰、韵达等为代表的快递业，以美团、达达等为代表的即时速送业，以百世、招商为代表的仓储业。作为经济大国，中国的物流市场十分庞大，到2018 年为止，我国第三方物流规模就已经达到了2 400 亿美元，位居世界前列。物流已经是市场经济的重要一环，连接着各行各业，联通着千家万户，是加快经济发展、保障民生建设的重要内容。

然而，随着“新冠肺炎”疫情不断蔓延，全国各地的铁路、公路、水路、民航运输都受到了严重的影响。我国也开始出台限制国外航班、轮船、旅客等的入境和登陆，这次突然发生的“黑天鹅”事件，给我国物流行业带来了空前的影响。疫情的巨大冲击下，市场需求降低，客户订单减少，生产活动受限，市场竞争加剧，各企业都面临着盈利困难、收益下降的局面，同时，由于终端零售市场的需求急剧下降，导致进出口贸易受到限制，总体利润下降。而采取隔离、限制人员流动等措施，会使工作效率下降，使得运输和物流成本也随之进一步升高。

一方面，物流企业因复工推迟而出现的人力和运力短缺，导致人力和时间成本上升；另一方面，在多数省份实施交通管制以后，由于道路规划的限制，导致了跨省的车辆绕行费用的提高，而且由于货运量的减少，导致了空驶率的提高，使得单车的运输费用也随之升高。综上，疫情的反复使得物流企业面对的风险加剧，因此，研究物流企业间的风险溢出效应对物流企业的风险防范有着重要意义。

1 计量模型

1.1 CoVar 模型。CoVaR 这个概念来源于VaR，它的经济意义是指一个企业发生风险时，另一个企业因此而承担的总体风险价值。VaR 表示在某一置信水平下，一个机构可能会遭受的最大损失，VaR 一般表达式为：Prob（ΔP ＞Va R）=1-T，而CoVaR 一般表达式则为：机构i 在机构j 发生风险的情况下所承担的总体风险是其中机构i 本身的自由风险为VaRi，剥离其自由风险后采用增量来表示机构j 给机构i 带来的风险，表达式：

1.2 DCC-GARCH 模型。DCC-GARCH 模型是Engle 将CCC-GARCH 模型常数相关假设进行改进得到的动态条件相关GARCH模型，主要用于描述不同变量间动态变化关系和相互影响，可以较好刻画时变非线性相关关系，其一般步骤是先计算单变量GARCH 模型，后通过所得参数计算多变量间的相关系数ρ。GARCH 模型（以GARCH（1,1）为例）一般表达式如下：

如果涉及到多变量，则涉及到矩阵和协方差概念，公式如下：

其中：为Ht条件协方差矩阵，Dt为条件标准差组成的对角矩阵，Rt为动态相关系数矩阵，Qt为协方差矩阵，Q*为经过残差标准化后的无条件协方差矩阵，为Qt的对角矩阵。

两变量间动态相关系数可以表示为：

1.3 DCC-GARCH-CoVaR 模型。在计算出前文DCC-GARCH 模型中动态相关系数情况下，VaR 和CoVaR 的表达式可以分别表示为：

其中：Q（q）为置信水平为1-q 时机构i 收益率所符合的分布下的q 分位数值，ρij,t为t 时刻下两变量间动态条件相关系数。

2 实证研究

2.1 样本选择及描述性统计分析。本文主要选择了顺丰控股和圆通速递两只股票日收盘价作为研究对象，原因是顺丰控股和圆通速递在我国物流公司里最具代表性。样本的起始日期是2021 年1 月1 日，截止日期是2022 年6 月30 日，所有数据均来自于新浪财经网站。在实证研究之前，先将原数据进行预处理，定义股票交易收益率为Rt=ln（Pt/Pt-1），其中：Rt表示当期收益率，Pt表示当日股票收盘价格，Pt-1表示前一日股票收盘价格。用这个方法计算收益率主要优点有：主要考察价格变动率，避免了波动性问题；计算复利时可以将其直接相加，便于直观地感受一段时间内的收益。

通过Eviews 绘制样本期间两支股票收益率趋势图，并观察其走势。

图1 描绘了两支股票的收益率序列，从图1 中可以看出，顺丰控股和圆通速递的股票收益率均在-0.1 和0.1 区间波动，且呈现出波动聚集特征，即高波动率和低波动率各自聚集在某一时间段。从波动幅度来看，圆通速递的收益率明显更为剧烈，即圆通速递在股票市场表现更为活跃，风险也更大。

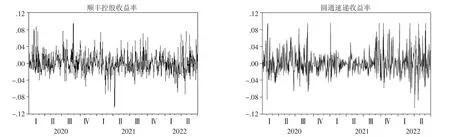
图1 顺丰控股和圆通速递股票收益率时间序列图

对两支股票收益率序列进行描述性统计，结果如表1 所示。从均值来看，两支股票收益率均为正。标准差通常被用于衡量数据波动程度，从标准差来看，圆通速递的标准差更大，表明圆通速递股价波动更剧烈，市场风险更大。偏度用于衡量数据的偏斜方向和偏斜程度，当偏度大于0 时，长尾在右，说明数据中位于平均值右侧的数据居多，从偏度来看，顺丰控股和圆通速递收益率序列长尾均在右边。峰度是一个对比特征量，对比对象为正态分布，它研究的是数据概率密度曲线分布在均值处的高低，当峰度大于3 时，则数据对于正态分布相对陡峭，存在尖峰厚尾特征，其出现极端值的概率也更大，如表1 显示，两支股票收益率序列的峰度均大于3，即都存在尖峰厚尾特征。从J-B 检验结果可以看出，两支股票收益率序列都在0.1 的显著性水平下拒绝原假设，即都呈现非正态分布。

表1 顺丰控股和圆通速递股票收益率序列描述性统计

2.2 实证分析

2.2.1 平稳性检验。平稳性检验是检验序列是否平稳，如果存在单位根，会使得回归分析中出现伪回归。当时间数多于截面数时，需要先进性平稳性检验。故本文使用常规的ADF 检验方法对两支股票收益率序列平稳性进行检验。结果如表2 所示：

表2 顺丰控股和圆通速递股票收益率序列ADF 检验结果

从表2 可以看出，顺丰控股和圆通速递收益率序列ADF 统计值均小于1%显著性水平下的临界值，即两个序列是平稳的，可以对其构建GARCH 模型。

2.2.2 ARMA-GARCH 模型估计结果。本文使用R 软件并基于AIC 信息原则，筛选顺丰控股和圆通速递收益率序列的最优ARMA 滞后阶数，对于平稳的收益率序列进行ARMA（p,q）模型定阶。建立GARCH 模型的前提是残差项的平方存在自相关性，因此本文先提取ARIMA 模型的残差进行LB 检验，防止影响下文结果，结果如表3 所示。

如表3 所示，p 值均不显著，即残差项不存在自相关性，接下来继续对残差项的平方进行LB 检验，结果如表4 所示。

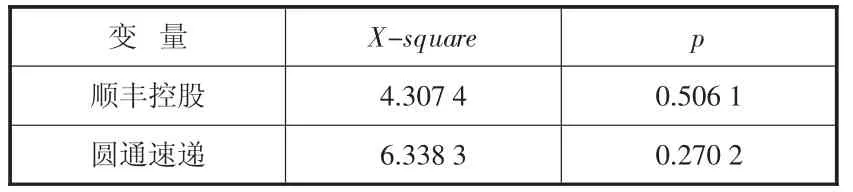
表3 残差项LB 检验结果

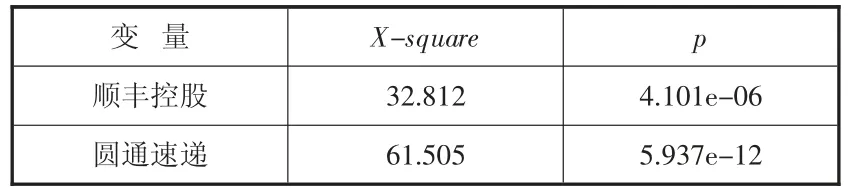
表4 残差项平方LB 检验结果

如表4 所示，p 值显著，接受原假设，即残差项的平方存在自相关性，可以对其构建GARCH 模型。

根据R 软件auto.arima 函数结果，对顺丰控股和圆通速递收益率序列都构建ARMA（0,0）-GARCH（1,1）模型，估计结果如表5 所示：

表5 单变量GARCH 模型估计结果

α 表示短期内股票对市场上新信息的敏感程度，（α+β）表示股票长期波动性趋势的持续性。从表5 可以看出，顺丰控股和圆通速递收益率序列模型参数均为正，且（α+β）值均小于1，满足模型的约束条件。从显著性上来看，除顺丰控股的α 值在0.05 的显著性水平下显著外，其他参数均在0.01 的显著性水平下显著。从（α+β）值来看，两支股票均比较接近1，说明所构造的GARCH 模型拟合情况较好。

2.2.3 DCC-GARCH 模型估计结果。根据前文所构建的ARMA-GARCH 模型，对顺丰控股和圆通速递收益率序列构建DCC-GARCH 模型，模型估计结果如表6 所示。

从表6 可以看出，DCC-GARCH 模型估计参数均为正数，且满足（α+β）值小于1 的约束条件，参数在0.05 显著性水平下显著。从结果来看，α 值越小，说明滞后一期的残差乘积对动态相关系数的影响越不明显，β 值越接近于1，说明前一期对两支股票的收益率序列相关系数影响越大，且两支股票的相关系数持续性较强。表6 结果显示，DCC-GARCH 模型估计的α 值较小，说明顺丰控股和圆通速递收益率序列动态相关系数受滞后一期的标准化残差乘积影响很小，而β 值较大，说明二者相关系数具有较强的持续性。二者动态相关系数时序图如图2 所示。

表6 DCC-GARCH 模型估计结果

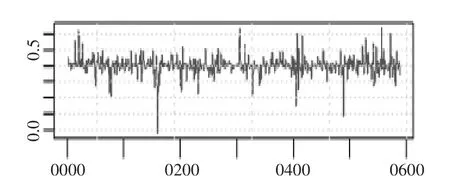
图2 顺丰控股和圆通速递收益率序列动态相关系数时序图

2.2.4 实证结果分析。从上文DCC-GARCH 模型所得到的结果，并结合ΔCoVar 计算公式，采用5%分位数水平对样本期间顺丰控股和圆通速递收益率序列极端风险溢出效应进行量化，得到二者间ΔCoVar 结果如图3 所示：

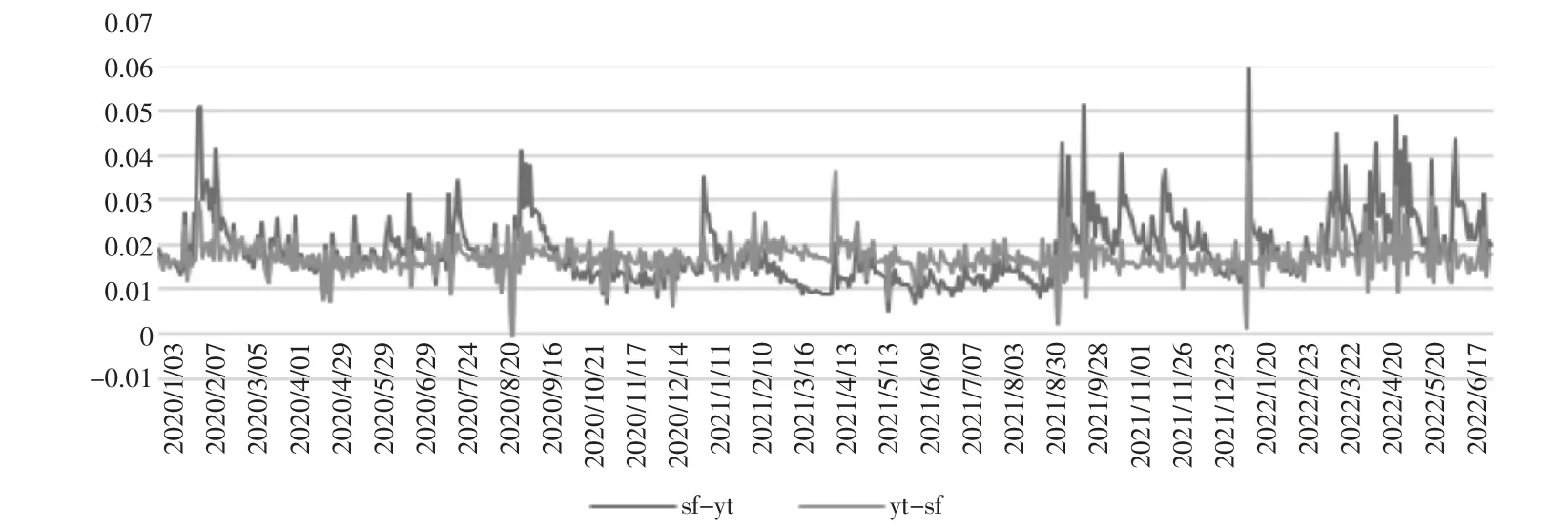
图3 顺丰控股和圆通速递收益率序列极端风险溢出效应

图3 给出了，当极端风险发生时，顺丰控股和圆通速递间动态风险变化情况，从溢出水平上来看，顺丰控股对圆通速递的风险溢出水平大于圆通速递对顺丰控股的风险溢出水平。这意味着，当物流市场发生风险事件时，顺丰控股对于圆通速递的风险传染程度更高。观察两条曲线走势可以发现，顺丰控股对圆通速递的风险溢出水平波动范围更大，整体溢出值在0 到0.062的范围内波动，这说明了当顺丰控股受到风险冲击时，更加容易快速做出反应，并向市场其他企业传播风险。相比下，圆通速递对市场的风险传染速度相对较慢。

具体分析两支股票风险溢出情况可知，溢出值在大部分时间较为稳定，在0 到0.04 的范围内小幅度波动，主要在2020 年2 月、2020 年9 月和2022 年1 月达到峰值，分别为0.05、0.05 和0.06，其原因可能在于，2020 年2 月，国内疫情处于开端，也是传染风险最大的阶段，政府对于物流的限制，导致了国内物流企业风险激增；2021 年9 月，中国物流与采购联合会公布的国内物流业景气指数为54%，同比上升了4.5 个百分点，物流行业内有“金九银十”的规律，并随着中秋、国庆两节的来临，物流需求趋旺，业务活跃，扭转了连续四个月回落的走势，物流企业业务激增；2022 年1 月，受到疫情影响区域、领域供给短缺，物流供需结构性失衡加剧，物流服务价格波动明显增大，加剧了物流业间风险传递。而通过观察图3 可以看出，顺丰控股和圆通速递收益率序列极端风险溢出效应在2022 年3 月至5 月，均有较大波动幅度，结合国内疫情分析，以上海、苏州为代表的华东地区，均呈现出情况严重、持续时间较长的疫情反复，这些经济发达的地区物流仓储库房和场站在疫情下停止运转了，整个分拣工作因此就无法完成，对物流业的冲击是非常明显的。