长江经济带物流业要素配置效率变化研究

唐建荣，何硕硕（江南大学 商学院，江苏 无锡 214122）

0 引言

物流业联结生产、流通和消费，是深度融合了运输、仓储、配送、信息、金融等功能的复合型服务产业。中国物流与采购联合会发布的统计数据显示，2010—2020 年，全国社会物流总额从125.4 万亿元攀升至300.1 万亿元，年均复合增长率达到9.12%，物流业促进国民经济发展的重要支撑作用日益显现。但我国物流业的高速增长在很大程度上依赖于生产要素无序的高投入和高消耗，这难以避免造成了要素配置扭曲，引发了各类生产要素过度消耗、配置效率低下等严重阻碍物流经济可持续发展的问题。随着我国经济逐渐步入新常态增长阶段，转变经济发展方式，提升经济发展质量，注重投入产出均衡发展，实现要素合理配置，已成为未来经济发展的现实取向。长江经济带覆盖沿江11 个省市，横跨我国东、中、西三大板块，具有显著的区位优势，其地区人口数量和生产总值占比均超过全国的40%，发展潜力巨大，具有重要的战略地位[1]。研究新常态下长江经济带物流业配置效率不仅对其物流业转型有重要的现实意义，而且对我国其他经济圈物流业高质量发展有示范作用。

物流业作为五大基础产业之一，是当今世界经济发展方式转型的重要领域，国内外学者围绕物流业发展质量进行了许多有益研究。田强等采用DEA-BCC 模型和Malmquist 指数模型测算了环渤海经济圈2007—2016 年的物流产业效率[2]；郑金娥等运用DEA-BCC 模型，对长江经济带11 个省份的物流业技术效率、规模效率和综合效率进行比较分析，并对各效率的收敛性进行了检验[3]；张云宁等采用DEA 模型与Malmquist 指数模型相结合，对长江大保护区域19 个省市物流产业效率进行分析研究，发现长江大保护区域物流效率呈现出“下游高、上游低”的阶梯式分布[4]；Kim Joohwan 等基于三阶段网络松弛测度（SBM）方法对23 家韩国沿海渡轮企业的相对运输效率进行了分析，发现与不考虑内部生产阶段的SBM 模型相比，采用三阶段SBM 模型研究的企业运输效率的差异化程度有所提高[5]；田雨等基于发展质量视角，通过DEA 模型和Malmquist 指数模型分别测算了中国区域物流产业静态效率和动态效率变化，并利用Moran's I 指数模型对我国区域物流产业效率的空间相关性进行检验[6]；郭诣遂从全要素生产率的视角，基于2008—2019 年的数据实证分析了长三角地区流通业效率及结构特征，发现长三角地区流通业的全要素生产率尽管一直处于提升的态势，但局部时段波动也是显著的[7]；张瑞基于超效率SBM 模型测度分析了2005—2019年中国30 个省市物流业的能源生态效率，并构建PVAR 模型考察能源生态效率与其影响因素之间的动态均衡关系[8]；曹光求应用DEA-Tobit 模型对2014—2019 年间福建省沿海四大港口的物流效率进行分析，发现四大港口的物流效率存在显著差异[9]。关于物流业发展质量的研究，大多数学者集中在全要素生产率层面，很少有学者从要素配置效率角度进行研究。本文在借鉴相关专家学者对于物流效率投入、产出指标选择研究的基础上，构建包含资本、劳动力、能源要素在内的随机前沿生产函数模型，从物流业全要素生产率中分解要素配置效率，根据随机前沿函数的估计结果测算物流业要素产出弹性，结合要素成本信息，考察2010—2019 年长江经济带物流业要素配置效率的增长变化，力求客观反应物流业要素配置现状及变化趋势，为决策部门的政策制定与实施提供参考依据。

1 研究方法和数据说明

1.1 物流业全要素生产率分解

借鉴Kumbhakar 的方法[10]，分解物流业全要素生产率增长率，建立随机前沿生产函数：

式（1）中：y 为物流业的产出，f（x,t,β）表示生产函数的前沿面，x 是物流业生产要素投入，β 表示待估参数，t 表示时间趋势，u＞0 为产出导向型生产非效率项。

式（1）两边取对数，然后对时间求导得：

式（6）中：等式右边前三项分别表示技术进步、技术效率和规模效应的变化，最后一项即为物流业要素配置效率的增长（ΔA E），通过物流业要素产出份额偏离其成本份额的程度和物流业要素投入资源的变化率来衡量：

1.2 物流业要素配置效率测度

测算物流业要素配置效率需要指定生产函数形式，较常使用的有柯布-道格拉斯（C-D）和超越对数生产函数两种形式。超越对数生产函数相较C-D 生产函数更具灵活性，在实证过程中可根据参数估计结果的显著性对变量进行相应调整，根据模型形式检验结果剔除不显著的冗余变量，确保估计结果的准确性，故本文选择超越对数生产函数。假定物流行业投入资本（K）、劳动力（L）、能源（E）三种生产要素，同时以时间趋势（t）衡量技术进步程度，则设立超越对数生产函数：

为避免错误函数形式造成随机前沿模型测算的结果出现误差，须检验式（8）的合理性，建立以下假设：

（1）H0: β5=β6=β7=β8=β9=β10=β11=β12=β13=β14=0，即生产函数选择含时间趋势变量的C－D 生产函数形式。

（2）H0: β4=β8=β11=β12=β13=β14=0，即不存在技术进步。

（3）H0: β12=β13=β14=0，即技术进步与投入要素无关，技术进步为希克斯中性。

（4）H0: β5=β7=β9=0，存在冗余变量。

（5）H0: η=0，表示技术效率不随时间变化而变化。

上述所有假设均是通过构建广义似然比统计量LR 来完成检验。具体方法为：按照检测要求分别进行随机前沿函数估计，根据LR=-2 ［L（H0）-L（H1）］计算LR 值，其中L（H0）和L（H1）分别为零假设H0和备择假设H1的似然函数值，备择假设H1为式（8）。统计量LR 服从自由度（k）为受约束变量个数的χ2分布，如果LR 值大于的临界值，则通过显著性水平5%的检验，拒绝原假设；反之，LR 值小于的临界值，接受原假设。检验结果如表1 所示，假设1、2、3、5 均被拒绝，说明选择超越对数生产函数形式是正确的。假设4 的检验结果为接受，表示确实存在冗余变量。去除冗余变量后的生产函数为：

表1 随机前沿生产函数形式检验结果

对式（9）的所有参数β 进行估计，根据结果可以计算得出资本要素产出弹性劳动要素产出弹性能源要素产出弹性为：

根据式（10）、式（11）、式（12）的结果，再结合式（7），即可得出资本、劳动、能源要素配置效率的变化率以及物流业要素配置效率的变化率。

1.3 数据选择和处理

由于目前我国物流产业没有完整的数据统计体系，结合交通运输、仓储和邮政业的增加值占物流业增加值85%的事实，本文参考唐建荣等的方法[11]，以交通运输、仓储和邮政业的统计数据代替物流产业的发展水平。本文使用的数据主要来自历年各地区统计年鉴和《中国统计年鉴》以及《中国能源统计年鉴》，样本为2010—2019 年长江经济带11 个省市区面板数据，主要有以下变量：

（1）物流业产出：选取各地区物流业的增加值作为物流业产出指标，并采用分省市的GDP 平减指数将其折算到以2010年为基期的不变价格。

（2）资本要素投入及其成本：本文以物流业的资本存量作为资本要素投入，使用永续盘存法对其进行估算，计算公式如下：

其中：Ki,t、Ki,t-1分别指i 地区t 年和t-1 年的物流业资本存量；Ii,t为地区年物流业固定资产投资额，选取各地区物流业固定资产投资额衡量，并通过固定资产投资价格指数折算到2010 年为基期的不变价格；σ 表示物流业资本折旧率，参考田有春等[12]的研究将其设为4%。基年资本存量使用增长率估算法来估算，计算公式为：

式中：g 为2010 年附近的固定资产投资稳态增长率，此处取2010—2019 年各省市物流业固定资产投资的年均增长率。资本要素投入成本即资本要素投入与资本要素价格的乘积，本文用中长期贷款利率作为资本要素的价格，数值取5 年期金融机构人民币贷款官方基准利率。

（3）劳动力要素投入及其成本：理论上劳动力要素投入应该综合考量劳动力的数量、质量及工作时间，但因缺乏劳动力质量和工作时间数据，本文选取物流业年末从业人员数量作为劳动力要素投入指标。劳动力要素投入成本即劳动力投入与劳动力价格的乘积，选取物流业从业人员的人均工资作为劳动力投入的价格，并用居民消费指数折算为2010 年为基期的不变价格。

（4）能源要素投入及其成本：选取物流业能源消费总量作为能源要素投入指标。根据长江经济带各省市能源平衡表，物流业各行业消耗的能源主要有原煤、焦炭、汽油、天然气、电力等，用标准煤指数将其统一转换为万吨标准煤，得到每个省市物流业能源消费总量。能源投入成本的计算参考孙传旺等的处理方法[13]，将能源消耗分为煤炭、石油、天然气和电力四类，能源要素投入成本为这四类成本之和，并用主要燃料购进价格指数折算为2010 年为基期的不变价格。

2 实证结果分析

2.1 长江经济带物流业要素产出弹性分析

在随机前沿分析的理论基础上，采用以上相关指标的数据，运用Frontier4.1 软件对超越对数生产函数的估计结果如表2 所示。

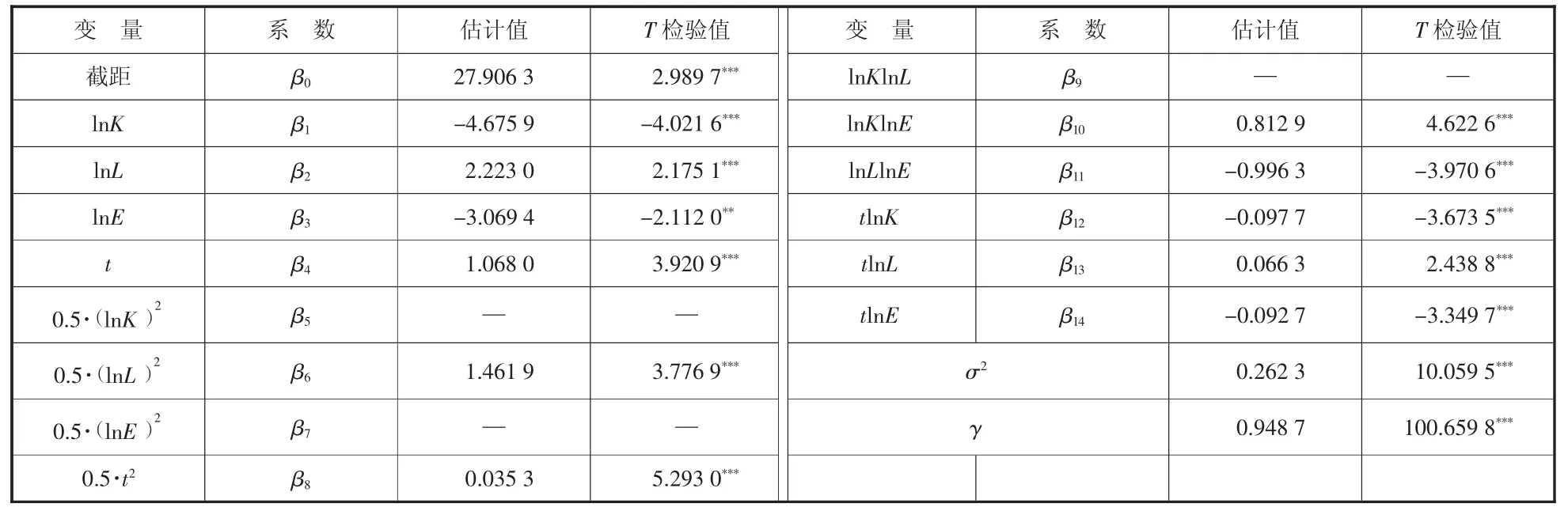
表2 随机前沿生产函数估计结果

据表2 可知，技术非效率方差在总方差中的比重达到0.948 7，且通过了1%水平的显著性检验，说明误差方差大部分来自于技术非效率项，且超越对数生产函数的所有参数均在5%的置信水平下显著，说明模型具有较好的解释力。值得特别注意的是，资本要素和能源要素交互项的系数为正值，说明资本和能源要素之间存在正向的交互作用，一要素的增加，能够提高另一要素的产出弹性。资本要素和劳动力要素交互项的系数为负值，说明资本投入与劳动力投入的交互作用是反向的，两者之间具有替代效应。资本时间变量和能源时间变量的系数为负，说明随着时间推移，资本和能源投入不再有助于物流业产出，即资本和能源要素投入出现了节约型技术进步。

依照国家统计局口径，把长江经济带划分为：下游、中游、上游。下游包括上海、江苏、浙江、安徽；中游包括江西、湖北、湖南；上游包括重庆、四川、贵州、云南。假定长江经济带及其上中下游区域各为一个研究样本，各样本的省际要素平均投入量生产样本的省际平均产出，根据式（10）、式（11）、式（12），结合生产函数系数估计结果，计算出长江经济带物流业全带及其上中下游区域各要素的产出弹性，具体如表3 所示。

物流业生产要素的产出弹性反应了物流业生产要素投入变动对产出变动的影响程度。由表3 可知，2010—2019 年长江经济带物流业各要素产出弹性，资本、劳动和能源要素投入的年均产出弹性分别为0.535、0.352 和0.454，这表明资本、劳动力、能源投入都是物流业产出提升不可或缺的因素，但资本投入是10 年间长江经济带物流业产出的主要贡献来源。分区域看，长江经济带下游、中游、上游物流业的各要素产出弹性存在着显著的差异：资本要素年均产出弹性从下游到上游逐地区减少，资本要素对地区物流业产出增加的贡献逐渐减少，与资本要素相反，能源要素年均产出弹性从下游到上游逐地区增加。下游地区的劳动力年均要素产出弹性显著高于其他两个地区，中游和上游的劳动力年均产出弹性之间差异较小。

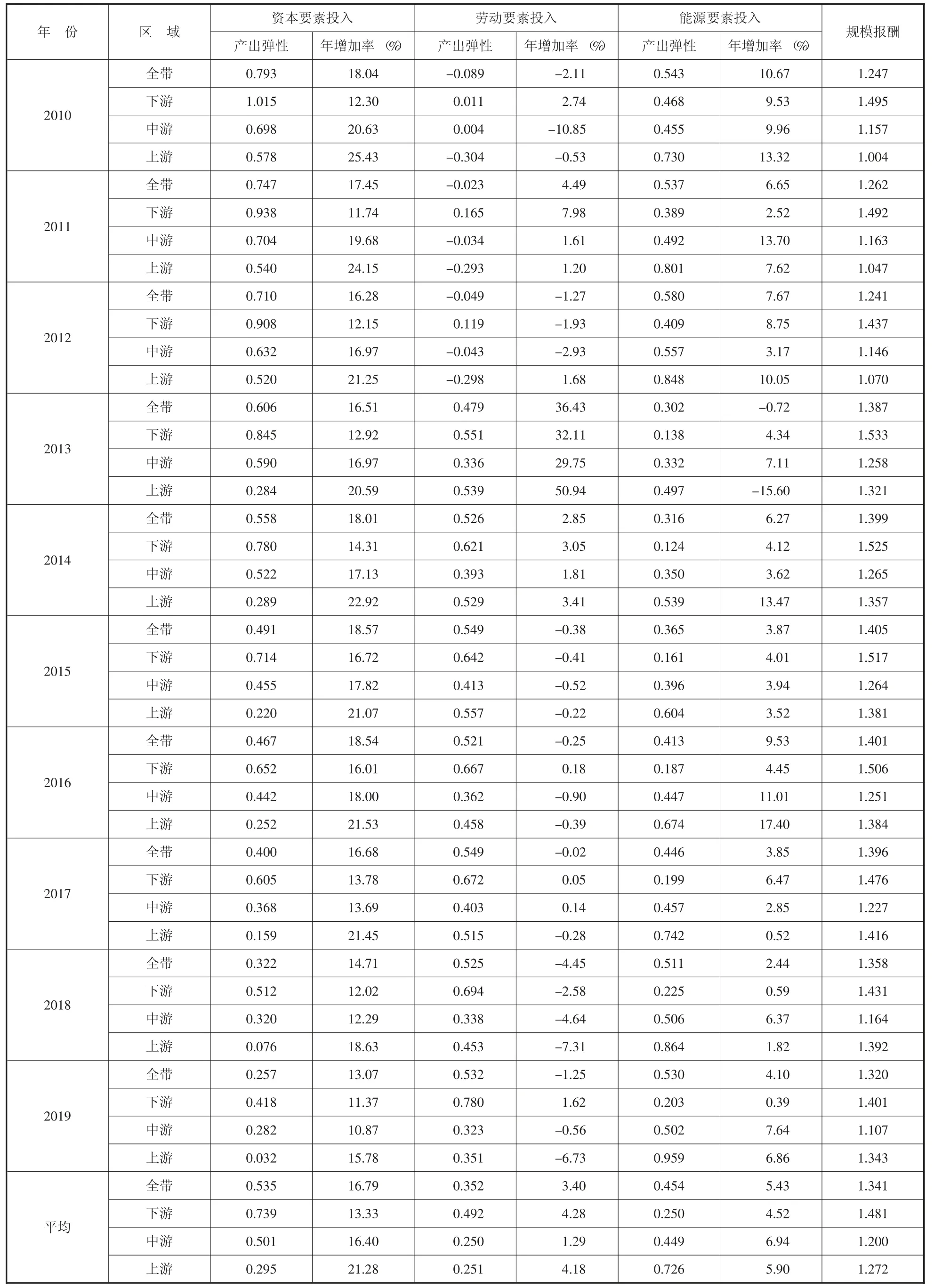
表3 长江经济带物流业各要素产出弹性及投入增长率

从要素产出弹性的变化趋势来看，2010—2019 年全带资本要素产出弹性呈现逐年下降的态势，从最初的0.793 下降到0.257，而资本要素投入的年增加率却保持在13.07%～18.57%之间，这表明长江经济带物流业资本投入逐渐饱和，呈现出边际产出递减的特征。与资本要素产出弹性不同，2010—2019 年长江经济带物流业劳动力要素的产出弹性表现出明显的阶段性特征：2010—2012 年物流业劳动力要素产出弹性处于负区间，2013 年大幅上升至0.479，并且于2013—2019 年之间保持小幅度波动变化。能源要素产出弹性表现出“高-低-高”U 型波动的变化态势，2010—2012、2018—2019 年能源要素产出弹性为0.5 以上的高产出弹性，2013—2017 年能源要素产出弹性相对较低。各地区要素产出弹性变化趋势与全带相似，不再赘述。从总体规模报酬来看，2010—2019 年长江经济带全带及其各区域要素产出弹性之和均大于1，长江经济带物流业规模报酬递增，这反应了长江经济带物流业具有一定的规模效应，扩大产出规模可以提高效率。

2.2 长江经济带物流业要素配置效率变化分析

根据式（7）可以得知要素配置效率的变化主要由两方面决定：一是要素产出份额与要素成本份额的差值，即要素扭曲程度；二是要素投入增长率。在完全竞争市场条件下，要素的产出份额与要素投入的产出份额相等，要素配置不存在扭曲。但从实际结果来看，2010—2019 年长江经济带物流业要素产出份额与成本份额并不相等，要素配置存在不同程度的扭曲。

图1 呈现了2010—2019 年长江经济带物流业要素配置效率增长率的变化。物流业要素配置效率增长率大体上呈现下降的趋势，要素配置效率变化表现出明显的阶段性特征：2010—2013 年配置效率变化为正增长，这个阶段物流业要素配置状况逐年改善。2014—2019 年要素配置效率为负增长，从2004 年的负增长1.6 个百分点，到2019 年的负增长4.6 个百分点，要素错配问题逐年加重。其中，资本要素配置效率增长率表现出大幅波动的特征，主导了要素配置效率增长率在样本期间的变动趋势。

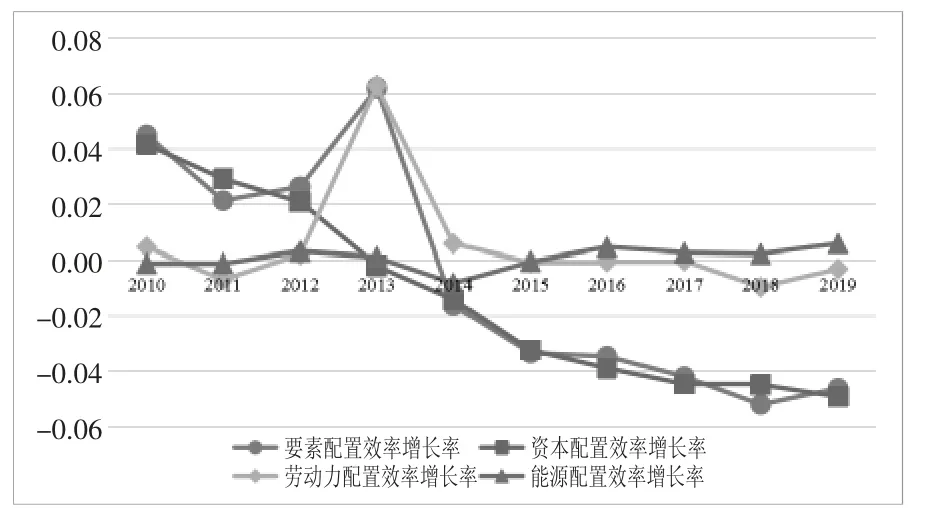
图1 长江经济带物流业要素配置效率增长率

从各要素的配置效率增长率变化趋势上来看，资本要素配置效率的增长率逐年下降，并且于2014 年降为负值，资本配置效率开始出现负增长，主要原因在于长期以来我国经济过于依赖投资驱动，资本要素投入保持快速增长，资本要素成本逐年增加，而其产出弹性显然受到边际产出递减的约束。2015 年我国提出供给侧改革，指出用改革的办法推进结构调整，矫正要素配置扭曲，也从侧面印证了这一结论。劳动力要素配置效率增长率于2013 年达到最大为0.063，其余年份均维持在-0.01～0.006 区间之间，保持较小的波动。究其原因，2013 年国务院对物流业进行了一系列改革，首先，撤销铁道部，组建国家铁路局和中国铁路总公司，将原铁道部部分职能划入交通运输部；其次，制定政策减少下方投资审批、生产经营活动审批事项，减化资质许可和认定流程，改革工商登记制度。这一系列改革措施为物流企业营造了宽松的经营环境，劳动力要素产出弹性得以释放，劳动力要素配置扭曲状态由负扭曲转变为正扭曲，同时大量人员进入物流业，劳动力投入大幅增加，劳动力要素配置状况大幅改善。相较于资本和劳动要素，能源要素配置效率增长率整体上波动较小，能源要素配置效率增长率于2014—2016 年，表现出了研究期间的最大涨幅。2015 年的石油价格因国际市场供过于求而暴跌将近一半，作为物流业的主要能源消耗，石油的价格变化很大程度上决定了物流业能源投入的成本变化。能源要素投入成本的减少，使能源要素配置由负扭曲转变为正扭曲状态，但是，由于国家节能减排政策的限制，尽管价格下降，能源投入并没有出现大幅增加，没有出现类似2013 年劳动力要素配置效率大幅增长的情况。

2.3 长江经济带物流业要素配置效率变化的区域异质性分析

长江经济带各区域物流业省际平均产出规模呈现出显著的差异，2010 年下游、中游和上游地区物流业的省际平均产值（亿元）分别为1 051.59、677.37、409.22，表现为“下游-中游-上游”递减态势，并且下游地区显著高于其他两个地区。三个区域的物流业省际平均产值均逐年增加，于2019 年分别达到1 824.41、1 364.58、841.39，整体上仍然呈现“下游-中游-上游”递减态势，并且地区之间的差距开始加大。

长江经济带下游、中游、上游的要素配置效率增长率变化如图2 所示。在样本研究期间，长江经济带各地区物流业要素配置效率增长与其地区物流业产值规模相似，总体上表现为“下游-中游-上游”递减态势。下游地区要素配置效率增长率总体上表现为先上升后下降，2010—2013 年配置效率增长率为正，并且于2013 年要素配置效率增长率达到最大，此后增长率跌为负值，并逐年下降。中游和上游地区配置要素配置效率增长率均呈现波动式下降，但上游地区的下降程度远甚于中游。

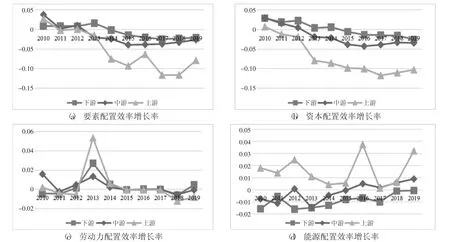
图2 长江经济带物流业要素配置效率增长率

从资本要素配置角度来看，长江经济带各区域物流业要素配置效率增长率均下降，但中上游地区下降速度显著快于下游地区，且研究期间只有下游地区资本要素配置效率呈现正增长，年均增长率为0.05%。中游和上游地区资本要素配置效率均为负增长，上游地区资本要素配置效率的负增长程度远甚于中游地区，年均增长率为-7.1%。各地区资本配置效率变化的差异大体表现为“区域物流业省际平均产值规模高—资本要素产出弹性份额大—资本要素配置效率增长率高”的特征。这主要是因为：物流业省际平均产值规模较高的区域，依托较高的市场化程度、充分发展的非国有经济及优良的法治环境等优势条件，促使市场竞争机制发挥强有力作用，为资本投入的高效利用提供良好外部环境，表现出更高的资本要素产出弹性及份额。同时，这些区域的物流业已初步形成一定规模，处于向高端化的攀升阶段，提供的物流服务也相对趋于高附加值，使得资本要素产出弹性及其份额更高。从劳动力要素配置角度来看，除2013 年的大多数年份，长江经济带各区域物流业劳动力要素配置效率增长率差异甚微，2013 年各区域劳动要素配置增长率均有不同程度的增长，但上游地区增长幅度最大。这主要得益于2013 年国务院推进的一系列改革，尽管中下游地区劳动力要素产出弹性和劳动力投入都有不同程度增长，但上游地区增长幅度显著高于中下游地区，劳动力产出弹性由-0.298 增长至0.598，劳动力投入增加率高达50.94%。从能源要素配置角度来看，长江经济带下游、中游、上游的能源要素配置效率年均增长率分别为-0.9%、-0.1%、1.5%，与地区产值规模的变化态势相反，表现出“下游-中游-上游”递增的态势，且上游地区远高于中下游地区。究其原因是上游地区和中下游地区相比，其物流业内部结构相对不合理，高耗能传统物流企业对地区物流业发展做出了重要贡献，致使其能源要素产出弹性相对较高。

3 结论和建议

基于长江经济带物流业省级面板数据，本文构建超越对数生产函数对2010—2019 年长江经济带物流业投入产出系统中的要素产出弹性、要素投入增长率、要素配置扭曲程度以及要素配置效率增长率进行了测算和分析。得出以下结论：第一，资本要素投入是长江经济带物流业增长的主要贡献来源，但由于边际产出递减，资本要素对物流业增长的贡献逐年减少。第二，长江经济带物流业要素配置效率增长率大体上呈现下降的趋势，下降原因主要是长期以来投资驱动发展导致的资本要素错配问题加重。从分区域视角来看，物流业要素配置效率增长表现为“下游-中游-上游”递减，符合我国物流业经济发展基本状况，即物流业省际平均产值规模较高的地区，其要素配置效率相应较高。第三，长江经济带物流业的资本、劳动、能源要素配置效率增长变化存在显著差异。资本要素配置效率增长率变化幅度最大，由2010 年正增长4.5%，到2019 年负增长4.9%，劳动要素和能源要素配置增长率大多数年份均在-1%～1%之间变动。原因在于资本要素配置的扭曲程度及资本要素投入增长率均为最大，且远远高于劳动和能源要素。分区域看，资本要素配置效率增长差异与地区内服务业省际平均产值规模相似，表现为“下游-中游-上游”递减，能源要素配置效率增长与之相反，劳动力要素配置效率增长的地区差异最小，并且表现出趋同的趋势。

基于上述研究结论，为提高长江经济带物流业要素配置效率，改善长江经济带物流业要素配置状况，提出以下政策建议：

（1）深化改革，扫除要素配置障碍。当前我国正面临百年未有之大变局，经济发展面临结构性、体制性、周期性因素的多重制约，在这样的外部环境下，物流业要素配置问题已不容忽视，深化要素市场化配置改革具有重要的意义。资本要素市场化配置改革重在资本供给主导权的转换：放开金融服务业市场准入，增加服务小微和民营企业的金融服务供给，完善多层次资本市场，将资本供给的主导权从政府转向社会，让资本流向高产出弹性的地方，逐步改变资本要素配置负扭曲状态；劳动力要素市场化配置改革重在推进劳动力要素畅通有序流动：建立统一开放、竞争有序的人力资源市场，保障平等就业权利；全面实施居住证制度，健全以居住证为载体的城镇基本公共服务提供机制，减少长江经济带与其他地区以及长江经济带区域内劳动力流动的障碍；能源要素市场化配置改革重在新旧能源要素的迭代转换：鼓励创新，减少新能源要素进入的门槛，促进物流业能源要素投入的迭代升级，减少国家节能减排政策对能源要素投入的影响。

（2）依托网络，减少要素配置成本。互联网具有信息共享的优势，能够跨越地理限制，扩大资源流动和配置的范围，降低要素搜寻成本和交易成本。地方政府应完善互联网基础设施建设，鼓励本地区互联网的发展和普及，积极推动物流业接入互联网，制定线上要素市场的规章制度，充分发挥互联网对物流业要素市场化的促进作用，弱化要素流动边界，促使要素有序流动，改善要素配置状态。

（3）精准施策，解决各地突出问题。针对长江经济带下、中、上游物流业要素配置状况的的具体差异，应该因地制宜，制定适合各区域发展阶段的措施。长江经济带下游地区应利用其资本聚集和市场规模大的优势，集中力量于创新，以创新促优化。中游地区需加大对物流业从业人员培训的培训力度，以增加其产出弹性，减少日益增加的人力成本所带来的劳动力配置问题。上游地区需加强与下游地区的产业合作，以扩大物流业市场规模，利用规模效应提高物流业产出能力，改变当前高投入低产出的现状。