弦σ模型中的Ricci流扰动和Weyl反常系数

詹 路, 颜 骏, 黄 忆

(四川师范大学 物理与电子工程学院, 四川 成都 610101)

Ricci流方程是现代微分几何学中的一种重要的数学工具.1982年Hamilton[1]在研究正曲率3维流形时建立了这一方程∂gij/∂t=-2Rij,2002年Perelman[2]根据Ricci流方程和几何熵方法证明了任意3维紧致单连通流形均微分同胚于3维球面,即著名的庞加莱猜想.Ricci流方程可以用来研究不同类型的球定理[3],推广的弦Ricci流发展方程已被用于进行流形上的梯度估计[4],证明紧致化定理和存在完备的非紧致流形等数学问题[5-6].

另一方面,在理论物理中也存在和Ricci方程类似的重整化群流(renormalization group flow)方程.文献[7-10]在计算2+ε维非线性σ模型的β函数时独立发现了RGF方程;1985年Callan等[11]在计算玻色弦σ模型的β函数时得到了广义的GRF方程组,并从这些方程中导出了修正形式的Einstein引力场方程.Gan等[12]研究了快子场所满足的场方程,文献[13-14]进一步计算了玻色σ模型的3圈β函数,热β函数还可以用来研究弦宇宙学中的温度对偶性质[15].

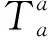
Ricci流方程或重整化群方程,在理论物理的各个领域中都有广泛的应用.如Einstein-DeTurck方程中可能存在Ricci孤子解[26],在2维空间上可以计算出Ricci孤子的质量[27],非平坦的Kahler度规也可以用来描述Ricci孤子[28],在文献[29]中分析了重整化群流作用下,Ricci孤子(或Witten黑洞)的线性稳定问题,结果表明Witten黑洞的线性扰动模是不稳定的.

在一些相关工作中,Ricci流方程或重整化群流方程,还被用来研究虫洞、黑洞和宇宙学中的各种物理问题.如根据数值计算方法讨论Ricci流中的虫洞几何结构的演化[30],分析Ricci流作用下2维面积和Hawking质量的变化规律[31]证明具有Gross-Perry-Yaffe负模类型的小黑洞在Ricci流作用下的不稳定性质[32],寻找2维时空中Ricci流方程的开弦和杂化弦黑洞解[33].Ricci流思想还被用来澄清Perelman熵和Bekenstein-Hawking几何熵之间的关系[34-36],研究结果表明Perelman所定义的熵和B-H熵并没有联系[37].另外,文献[38]根据重整化群流方程重新讨论了Einstein空间中标度因子的演化问题,结果发现在早期的轴子——Dilaton宇宙膨胀中,Hubble参量具有明显的振荡性质,但是最初的各向异性在随时间的演化过程中都将消失.

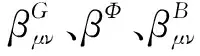
1 玻色σ模型中的重整化β函数

非线性sigma模型的作用量定义[10]为

(1)

其中,i、j是标量场的内部指标,μ是时空指标.背景场方法的出发点就是将场分解为一个经典场和一个量子场涨落场,又称为Schwinger-DeWitt技术,这一方法也被用于量子引力和弯曲时空量子场的重整化.通常的背景场量子分解是把φi在一些经典场组态φi附近展开为

φi=φi+πi,

(2)

其中量子涨落πi可看做一个扰动.假设πi是一个新的协变场ξi的函数,取φi为流形上在ξi上的切线矢量,于是可以把度规展开为ξi的幂级数

ξl1ξl2ξl3ξl4+…,

(3)

并且有

∂μ(φi+πi)=∂μφi+Dμξi+

(4)

所以作用量(1)式的在量子涨落背景下分解为

Ril1l2jξl1ξl2∂μφi∂μφj+

(5)

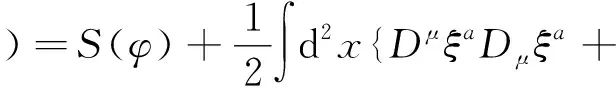
Riabj∂μφi∂μφjξaξb}+…,

(6)

其中

∂μξn-iAμabξb,

(7)

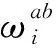
〈0|Tξa(x)ξb(y)|0〉=δabΔ(x-y),

(8)

得到其对有效作用量的贡献为

(9)

于是单圈重整化有效作用量成为

其中Rij是Ricci张量,这时非线性sigma模型的单圈β函数定义为

(11)

其中λ=Λ为动量截断参量.根据同样的思路可导出如下双圈β函数[37]

(12)

其中α为量子修正系数.类似的方法还可以计算弦理论中各种场的β函数,玻色弦的2维能动张量定义[37]为

(13)

其中,Xμ为弦坐标,α′为弦张力系数,γab为世界面度规,S为Polyakov弦作用量.弦的共形对称性(或Weyl对称性)将导致

(14)

所以经典玻色弦的能动张量迹为零.另外,背景场耦合的弦σ模型作用量为

iεabBμν(X))∂aXμ∂bXν+α′ΦR},

(15)

其中,Gμν是引力子场,Bμν是反对称张量场,Φ是Dilaton标量场.在文献[16-19]的一系列的工作中发现,重整化能量动量张量的迹可以用β函数表示为

(16)

其中3个系数表示背景场的单圈β函数,其表达式分别为:

O(α′2),

(17)

O(α′2),

(18)

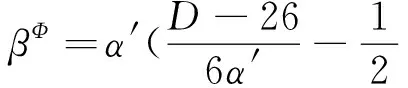
(19)

其中轴子场Bμν的场强定义为

Hμνk=∂μBνk+∂νBkμ+∂kBμν,

当时空维数取临界维数D=26,共形场中心元c=(D-26)/6为零,并且3个系数

这时Weyl反常将抵消,由(17)～(19)式可导出背景场的单圈Ricci流方程.如果引力场中存在一定形式的流扰动,或出现量子涨落的修正,那么Weyl反常系数可以不再为零,这时弦σ模型中将会出现共形反常.

为促进文化旅游可持续发展，丁蜀进行整体规划，精准定位，结合山水生态环境，致力打造紫砂特色小镇，统筹好当地的东坡书院、前墅龙窑、蜀山南街等文化历史遗存，以蜀山风景区为核心、以青龙河为带，重点建设集旅游、体验、制作于一体的紫砂文化旅游产业。告别粗放式单一性发展，以系统化、高质量发展思维，致力将丁蜀规划为集“陶瓷制作、陶瓷文化艺术交流、创意产品设计”的产、学、研、城一体化特色的文化体验与休闲度假宜居小镇，力争成为文旅创新的先导区，陶瓷设计创客的朝圣地，陶瓷艺术与经济的新地标。□

2 双圈Ricci流扰动下的Weyl反常系数

当轴子场Bμν=0,具有双圈量子修正的Ricci流方程组[39-40]为

(20)

(21)

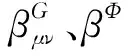
其中弦张力系数α′=ε≪1,表示一种弱耦合情况,当时空维数d=2时,c=-4,方程(22)求迹后有

再由(23)式有

(25)

根据(24)式得引力场的Ricci流扰动方程为

(26)

其中[]表示扰动后的表达式,将度规扰动设为

g00=α(x)+h(x,λ),

g11=β(x),g10=g01=0,

这里h(x,λ)≪α(x),于是有

(27)

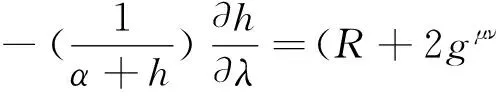
(28)

这时已忽略Rh的2阶小项,于是扰动方程变为

Rh+2(gμν∇μ∇νΦ)h(1-εR)+

(29)

另外,标量曲率扰动部份的表达式为

(30)

Dilaton场导数项扰动部份的表达式为

将(30)和(31)式代入(29)式化简后,得如下引力场的Ricci流扰动方程

(32)

在Dilaton场的Ricci流方程(25)中,有:

(33)

(34)

其中,g=α,β是度规的行列式,如果在方程(26)右边仅考虑引力场的Ricci流扰动,而Dilaton场不发生扰动,这时扰动后的Dilaton场方程成为

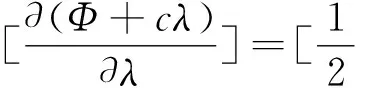
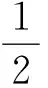
此时(35)式左边Dilaton场的扰动解设为

Φ(x,λ)=Φ(x)+φ(x,λ),

那么有

(36)

在推导Ricci流扰动方程(32)和(36)时,已假定引力场和Dilaton场的扰动系数和双圈量子涨落系数ε处于同一数量级,这时模型中同时考虑了扰动和量子修正2种效应的作用,这种作用使Ricci流扰动方程达到平衡.当引力场中不存在的流扰动或量子涨落的修正,那么由Ricci流方程组(22)和(23),可以得到度规α(x)和Dilaton场Φ(x)所满足的Cigar(雪茄)孤子解,Lambert等[29]曾研究过这类孤子在重整化群流的作用下的稳定性质.

这时,再根据(32)和(36)式可进一步导出h(x,λ)和φ(x,λ)所满足的量子扰动解.设

h(x,λ)=eQλf(x),

那么可以得到如下引力场和Dilaton场的Weyl反常系数:

(37)

其中,λ为Ricci流扰动参量,Q为扰动指数,f(x,Q)为扰动方程(32)的定态解,ε为弦张力系数,标量曲率的表达式为

(38)

因此,在非临界的2维玻色弦模型中,当存在Ricci流扰动或现量子涨落的修正,那么引力场和Dilaton场的Weyl反常系数均不为零,如果雪茄孤子解和量子扰动解可以求出,通过(37)和(38)式就可以导出2种场的Weyl反常系数的具体表达式.

3 单圈Ricci流扰动下的Weyl反常系数

当轴子场Bμν≠0,参数化后的单圈量子修正的Ricci流方程组[41-42]为

(39)

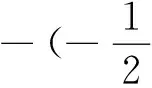
(40)

(41)

其中,Gμν为背景引力场,Φ为Dilaton标量场,Bμν为轴子场,中心元c=-4,轴子场的场强定义为

Hμνk=∂μBνk+∂νBkμ+∂kBμν,

(42)

度规扰动设为

g00=α(x)+h(x,λ),

Dilaton场的扰动设为

Φ(x,λ)=Φ(x)+φ(x,λ),

轴子场的扰动设为

Bμν=Bμν(x)+bμν(x,λ).

轴子场的矩阵设为如下形式

(43)

其中,对角元B00=B11=0,非对角元B01=B10≠0,轴子场强中的乘积分量为

(44)

在Ricci流方程组(39)～(41)中,Ricci张量的2个分量为:

(45)

Dilaton场的各个导数项分别为:

(46)

(47)

此时,没有扰动的Ricci流方程组的5个分量方程成为:

(49)

(50)

(51)

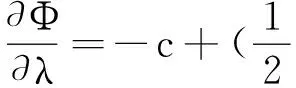
(52)

当

∂B01/∂λ=∂B10/∂λ=0,

由轴子场方程(50)和(51)解得

V0是积分常数.根据(44)～(52)式可导出如下完整形式的场方程组:

(54)

(55)

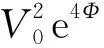
对Ricci流方程(39)求迹后得

(56)

引力扰动后的流方程变为

(57)

其中,Rh和[gμν∇μ∇νΦ]h都已经导出,由(30)和(31)式所表示,最后一项轴子场乘积项需要计算,这时有

(58)

所以得

(59)

于是扰动后的轴子场乘积项成为

(60)

根据(30)和(31)式,以及(60)式得到如下Ricci流扰动方程

(61)

(62)

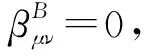
4 结论与讨论

本文主要研究了2维弦σ模型中,Ricci流扰动下的Weyl反常系数.在引言中简要回顾了Ricci流方程或重整化群流方程的研究历史和现状,还介绍了Weyl反常系数和β函数之间的关系,以及Ricci流方程在孤子、虫洞、黑洞和宇宙学中的各种应用.

在第1节中根据标量场的涨落技术和背景场展开方法,导出了玻色σ模型的单圈β函数,给出了弦σ模型中的能动张量迹的表达式,以及引力子场Gμν、轴子场Bμν、Dilaton场Φ的β函数公式.在第2节中研究了2维时空中的双圈量子修正下的Ricci流方程组,导出了引力场扰动h(x,λ)和Dilaton场扰动φ(λ)满足的微分方程组,给出Weyl反常系数的表达式.在第3节中研究了2维时空中轴子场作用下的Ricci流方程组,导出了引力场扰动h(x,λ),轴子场扰动b(x,λ)和Dilaton场扰动φ(λ)所满足的微分方程组,给出了Weyl方程系数的表达式.

β函数是研究量子电动力学(QED)的重整化性质时引入的概念,通常是指有效耦合常数或有效耦合质量随动量标度的变化率[45],在QED理论中β>0,有效耦合常数随动量标度的增加而变大,或随距离标度的增加而变小;在量子色动力学(QCD)中β<0,有效耦合常数随动量标度的增加而减小,或随距离标度的增加而变大,即QCD含有渐近自由的性质.在2维弦理论中,β函数表示引力子场扰动、轴子场扰动,以及Dilaton场扰动随动量标度的变化率.如果β函数都为正号,则扰动的变化和QED相似,随动量标度的增加扰动将增强;如果β函数都为负号,那么扰动的变化和QCD相似,随动量标度的增加扰动将减弱.

本文在一般的形式体系中研究Ricci流扰动方程和Weyl反常系数,当度规α、β、Φ场和Bμν场存在Ricci流孤子解时,就可以推导出度规扰动h(x,λ)的解析解,进一步计算出Weyl反常系数的具体表达式,并通过β函数的符号判定出3种场的扰动随动量标度的变化关系,这是下一步研究工作的一个主要任务.