RMC程序临界安全基准校验分析

周梦飞,吴晋营,邵 增,申鹏飞,2,杨海峰

(1.中国核电工程有限公司,北京100840;2.清华大学,北京100084)

核临界安全分析方法分为确定论方法和蒙特卡罗方法两大类。其中,由于蒙特卡罗方法可处理复杂能谱和几何系统而具有突出优势。随着大规模并行计算的发展,蒙特卡罗程序在核临界安全计算分析中得到了广泛应用,如国际通用蒙特卡罗程序MCNP和MONK等,以及国内自主开发的JMCT和RMC等。RMC程序(reactor Monte Carlo code)是由清华大学核工程物理系自主开发的3维蒙特卡罗输运计算软件,能处理复杂的几何结构、能谱和材料,根据实际问题进行临界问题本征值和本征函数计算[1-2],满足临界安全计算分析的基本需求。目前,针对RMC程序已陆续开展了基于VERA,Hoogenboom,BEAVRS等系列国际基准题的单棒、组件及全堆的测试验证,初步验证了RMC程序在堆芯核设计计算的准确性[3-6]。

但已有的验证实验多为压水堆的棒束模型,几何结构和材料选型相对单一,未能覆盖到压水堆以外的多数临界系统。因此,为将RMC程序应用于各类堆外易裂变材料系统的临界安全分析,有必要对RMC程序进一步开展包含不同系统构形、燃料类型、中子能谱、几何结构及不同的慢化剂、反射层、中子毒物材料的临界基准校验分析,为RMC程序对相应系统的适用性及不确定度提供完整的验证数据基础[7-9]。本文从临界安全基准实验国际评价数据库(international criticality safety benchmark evaluation project,ICSBEP)[10]中选取81个临界基准实验、共502个临界基准实验方案,开展RMC程序的临界基准验证分析。本文将RMC程序的计算结果与ICSBEP手册中给出的实验值进行了对比分析,对于偏差较大的基准实验采用国际通用蒙特卡罗程序作为参考程序进行计算,以验证程序计算结果的偏差来源。

1 基准实验分类

后处理厂的核临界系统涉及不同的裂变材料、系统结构及中子能谱等,因此选取了包含铀钚等不同易裂变核素的溶液、金属及化合物的快热谱等基准实验,本文所用临界基准实验汇总如表1所列。按照临界系统中主要不同的裂变材料将所选的基准实验划分高富集度铀(HEU)系统、低富集度铀(LEU)系统、铀钚混合(MIX)系统、钚(Pu)系统及233U系统5类。表1中：括号内的数字代表每类基准实验的个数;基准实验编号中的3个字母分别表示系统中的燃料种类、燃料形态(化合物-C、金属-M或溶液-S)和引发主要裂变反应的中子平均能量(能量高于0.1 MeV定义为快中子,记为F;能量低于0.625 eV定义为热中子,记为T)。所选用的临界基准实验在几何方面涵盖了棒栅、溶液、板、块、球及其阵列,与系统构造相关的输送管道和支撑台架等复杂结构;材料方面包括水、石墨及聚乙烯等不同的慢化材料,硼、钆及不锈钢等毒物材料,天然铀、铝、不锈钢及石墨等反射层材料;中子能谱方面涵盖了从热中子到快中子的大范围的中子能区,对RMC程序的验证计算提出了新的挑战。

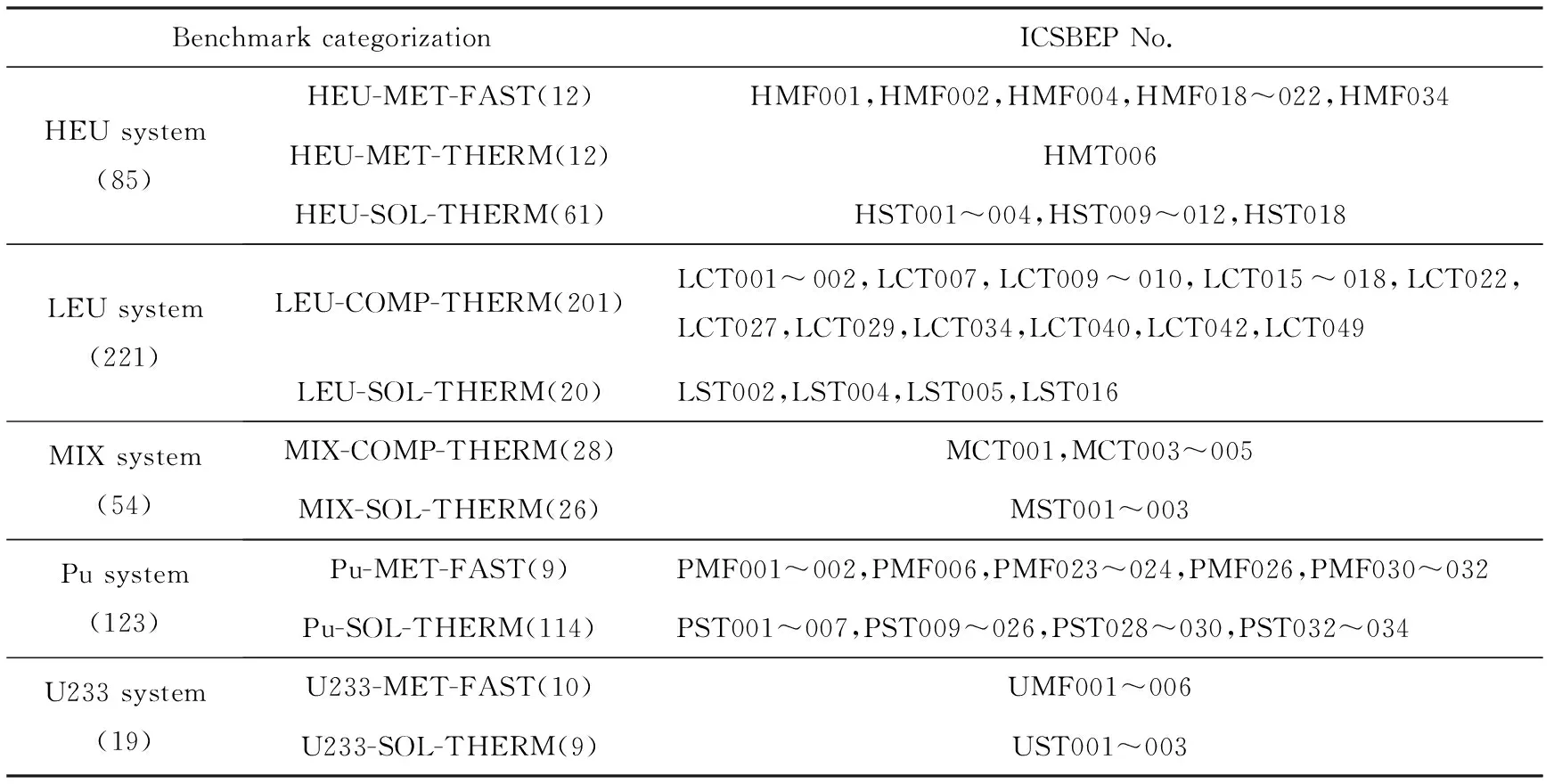
表1 本文所用临界基准实验汇总

图1为部分基准实验的RMC模型,分别为含管道的溶液系统、棒束系统和含支撑结构的多层板状系统。由图1可见,RMC程序对于复杂几何结构可实现很高的几何建模精度。

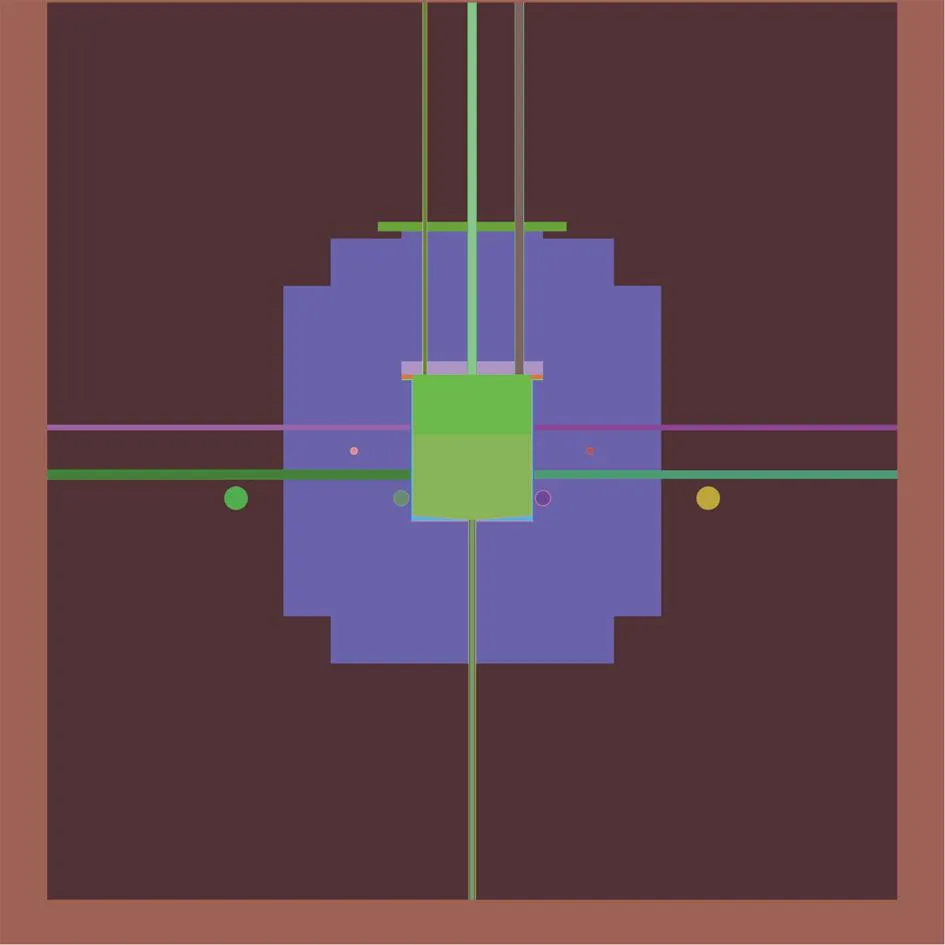
(a)PST019

(b)LST005

(c)HMF034

2 程序校验方法

为校验RMC程序对临界基准实验的有效增殖因子keff计算结果的准确性,首先需确立评价指标。ICSBEP手册中给出了每个临界基准题的有效增殖因子的实验测量值和测量不确定度[10],分别记作keff,e和σe。RMC程序临界计算得到每个系统的有效增殖因子及其不确定度分别记作keff,c和σc。本文用于评价RMC程序计算准确度的主要指标为计算值与实验值之比C/E、相对偏差δk、联合不确定度σt及σ的倍数Tσ,表示为

(1)

(2)

(3)

(4)

其中,角标e和r分别指代实验测量值和参考程序计算值。

3 基准实验计算结果

采用RMC-3.5.1程序对上述临界基准实验进行模拟计算。建模过程中按照文献[10]的描述精确考虑了各类系统的几何结构,临界计算中采用的核截面为基于ENDF/B-VII.1评价核数据库加工而成的300 K(室温)温度点下的ACE格式数据库。由于临界实验的产热极小,因此忽略实验过程中可能导致的温度变化,这一近似处理的偏差对计算结果来说是可接受的。计算中每代模拟的粒子数不低于10 000 ,计算结果的不确定度小于10-3。

图2 为临界基准实验的RMC程序计算结果。表2为临界基准实验C/E值的统计分析。

(a)HEU system

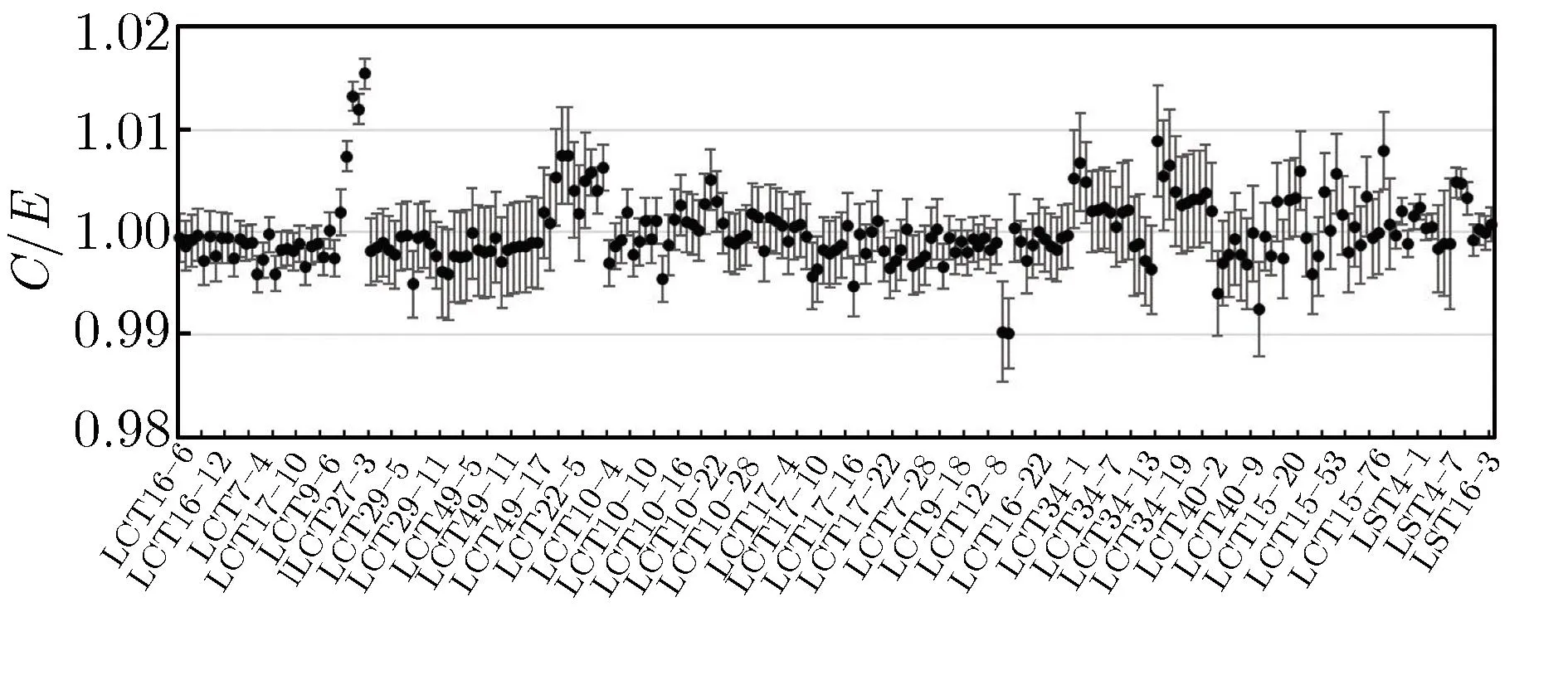
(b)LEU system

(c)MIX system

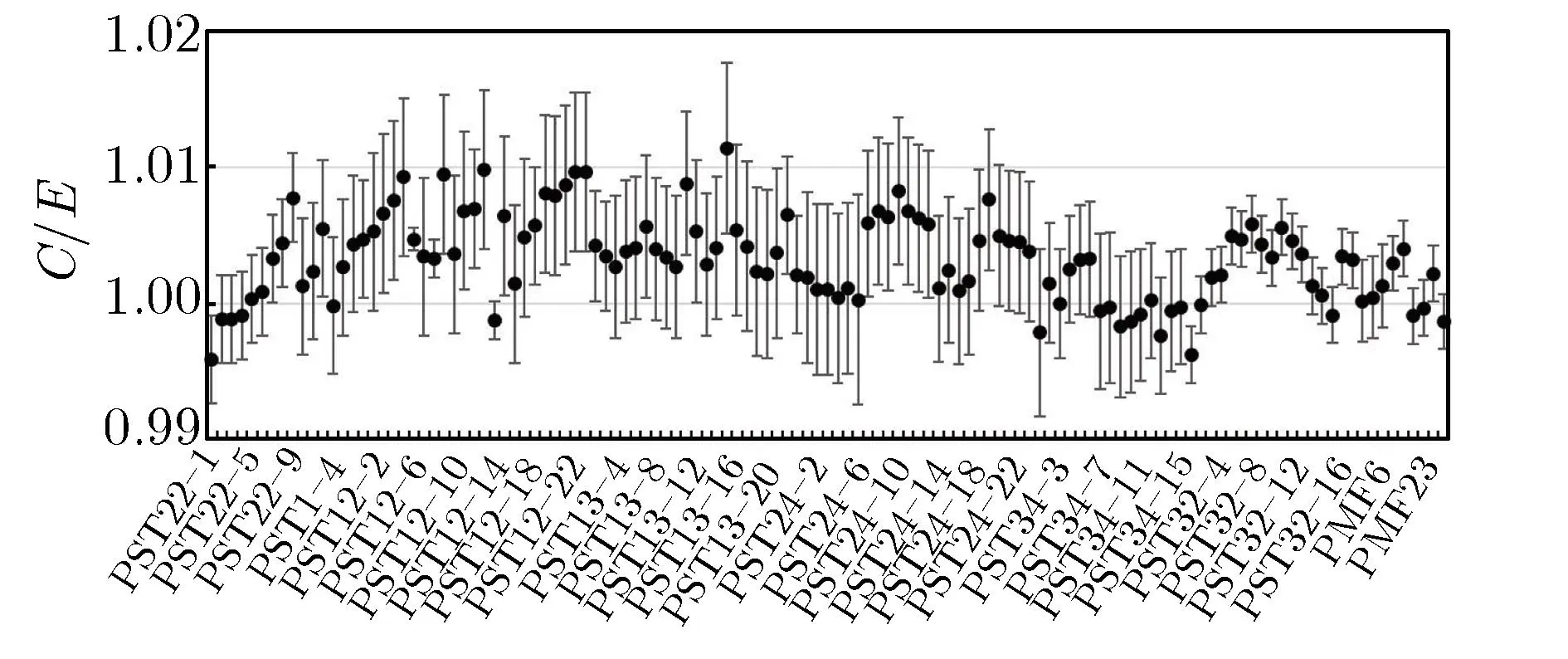
(d)Pu system

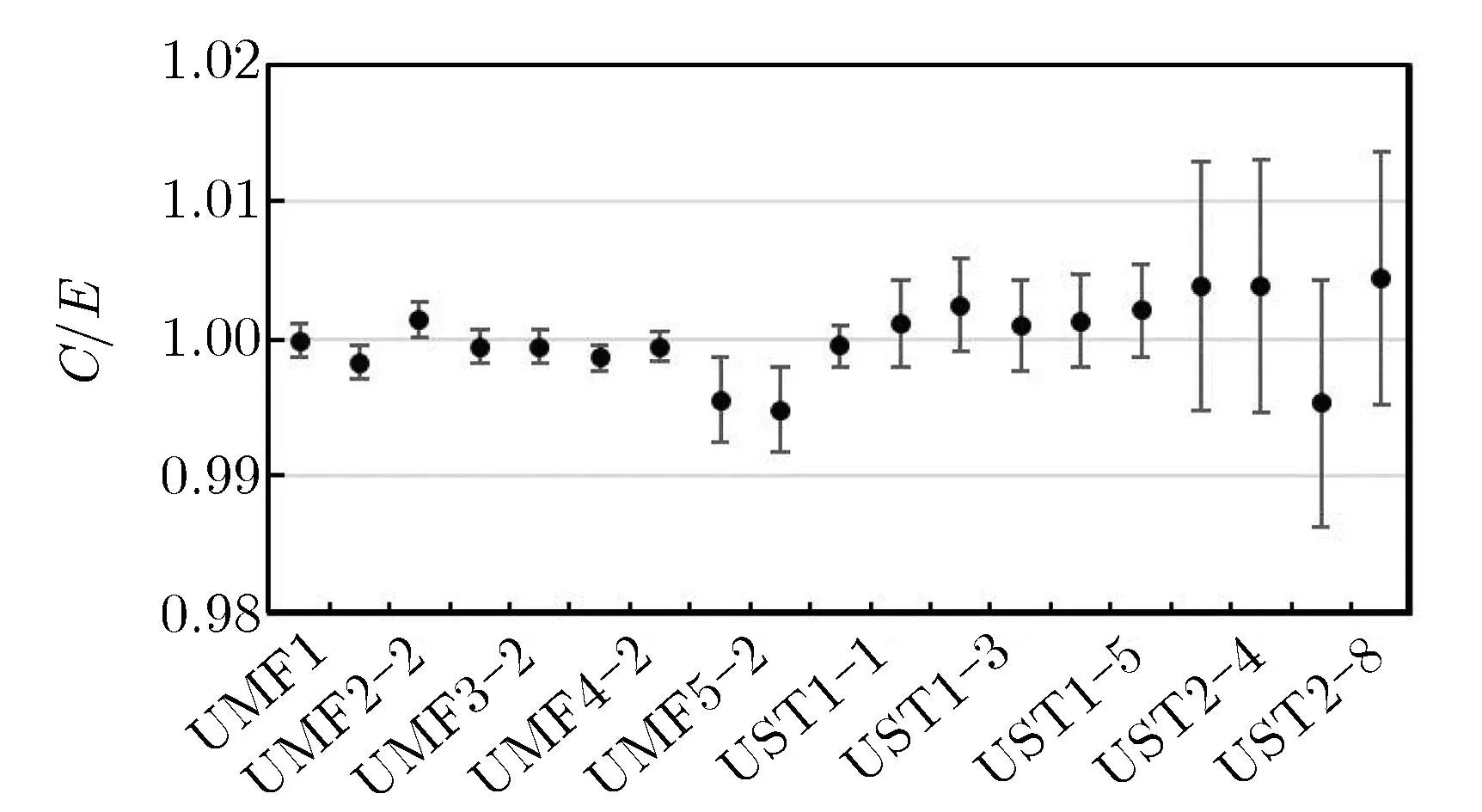
(e)233U system

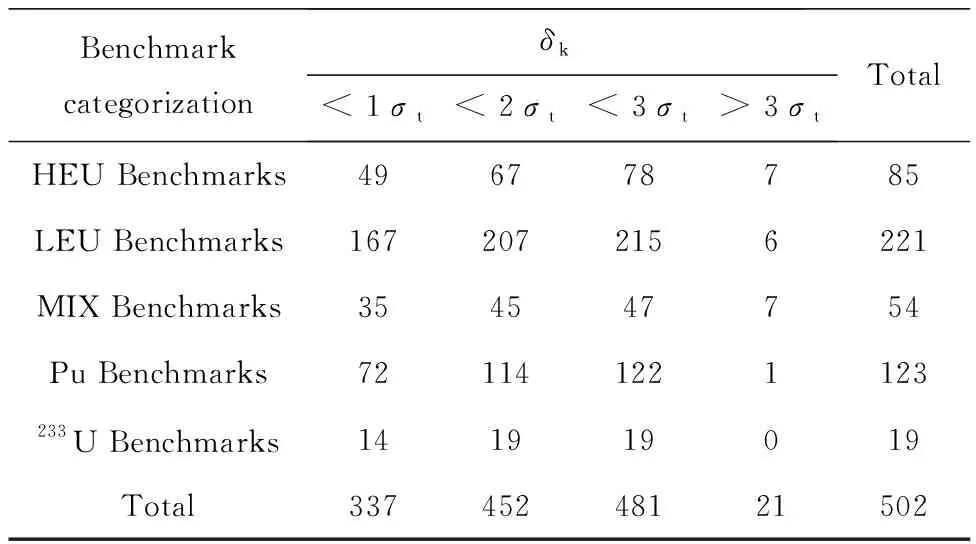
表2 临界基准实验C/E的统计分析

由表2可知,RMC程序的计算结果总体上与实验值符合良好,在所验证的502个基准实验中,有481个基准实验的相对偏差δk在3σt以内(置信度为99.67%),占所验证实验总数的95.8%;但仍有21个基准实验(如HST18,LCT27号实验等)的程序计算结果与实验值存在较大偏差,相对偏差超过了3σt。本文将对这些相对偏差大于3σt的基准实验,使用国际通用蒙特卡罗程序作为参考程序进行重新计算,以验证程序计算结果的正确性,分析偏差来源。

4 偏差分析

针对第3节所述21个相对偏差超过3σt的临界基准实验的偏差分析如表3所列。

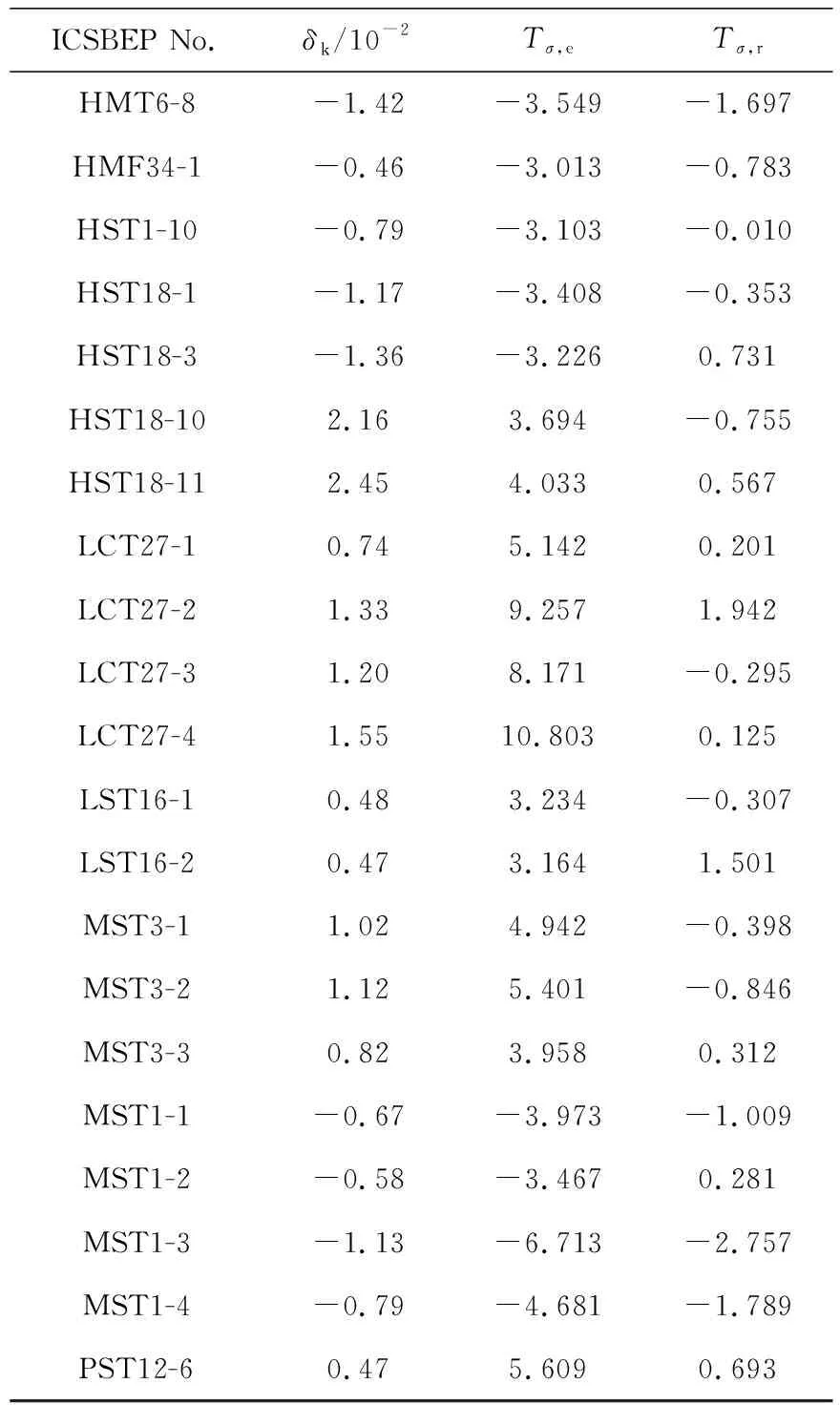
表3 临界基准实验偏差分析

表3中各项数值的计算公式已在第2节中给出。由表3可知,对于HMF34-1,HST1-10,LST16-1,LST16-2等10个基准实验,RMC计算值与实验值之间的相对偏差较小,小于1%,但相对偏差大于3σt的主要原因是实验测量的相对偏差很小,仅约为10-3。以PST12-6号基准实验为例,实验测量的相对偏差仅为6×10-4;HMF34,LCT27,LST16,MST1和MST3号基准实验测量的相对偏差分别为1.3×10-3,1.2×10-3,1.3×10-3,1.6×10-3,2×10-3,达到了很高的测量精度。

由表3可知,RMC程序的计算值与参考程序的计算结果符合得很好,偏差均在3σt以内,这也进一步说明了RMC程序具有与国际通用蒙特卡罗计算程序相当的计算精度,验证了RMC程序的计算准确性。而程序计算值与实验值之间的偏差可能是来源于所用核截面数据的偏差。Zheng等[11]对不同版本的ENDF/B截面库的研究表明,使用更新版本的数据库有利于获得与实验值符合更好的计算结果。

5 研究数据应用

进行临界基准实验校验分析的主要目的是为RMC程序的工程应用提供数据支持。因此以装载AFA3G组件的乏燃料运输容器为例,给出RMC程序计算此类系统的计算方法偏倚及不确定度。采用新燃料假设,燃料富集度均取为4.0%;容器的中子毒物板材料为硼铝合金,内部结构材料为不锈钢,容器筒体外布置铅屏蔽层,事故工况下考虑容器内部进水。根据上述条件,利用自主开发的相似性分析程序,选取相似性指标Ck>0.8的64个基准实验方案进行分析(Ck值由分析例与基准实验例关于核截面的协方差用方差归一后得到)。所选实验方案均为低富集度铀棒栅结构,燃料富集度范围为2.35%～9.83%,燃料棒的栅距范围覆盖了所分析的乏燃料组件,系统内含有硼钢或镉等不同材料的中子吸收板,适用于本例分析。根据所选基准实验方案的验证数据,取每个实验方案的实验相对偏差σe,i和计算相对偏差σc,i进而得到总相对偏差σt,i,表示为

(5)

利用权重因子1/σt2得到加权后的keff关于平均值的方差,表示为

n=64,i=1,2,3,…,64

(6)

平均总不确定度表示为

(7)

于是得到合并方差的平方根,表示为

(8)

由式(5)～式(8)可知,RMC程序计算该容器系统临界问题的偏倚值Bbias表示为

(9)

根据T分布表,可查得自由度为63(n-1)时,达到95%的置信水平时的系数μ为1.998 3。因此,计算方法的不确定度IM可表示为

IM=|Bbias|+μ·SP=0.000 795+

1.998 3×0.004 096=0.008 98

(10)

由式(10)可知,RMC程序计算该容器临界安全问题时的方法不确定度小于0.9%,进一步验证了RMC程序计算临界安全问题的准确性。

6 结论

本文从国际临界安全基准实验手册ICSBEP基准实验数据库中选取了502个临界基准实验方案,对国产自主化蒙特卡罗分析程序RMC进行了临界基准验证。所选取的基准实验按照所含核燃料的不同分为高富集度铀、低富集度铀、铀钚、钚及233U共5类临界系统,且涵盖了化合物、溶液、金属等不同的燃料形态,不同的系统结构和燃料富集度,中子能量的快、热能区,以及不同慢化剂、中子毒物和反射层材料的选择等。使用C/E值、相对偏差δk、联合不确定度σt和σ倍数Tσ等指标来评价RMC程序的计算准确度。计算分析结果表明,RMC程序计算值与基准实验值具有很好的一致性,在所验证的502个基准实验中,有481个基准实验的程序计算结果与实验值的相对偏差在3σt以内,占实验总数的95.8%,证明了程序具有很好的计算准确度。对其余21个相对偏差超过3σt的基准实验,采用参考程序计算进行对比验证,结果表明,RMC程序与参考程序的计算结果符合良好,说明了RMC程序具备与国际通用蒙特卡罗分析软件相当的计算精度。最后以乏燃料运输容器为例分析了RMC程序应用于工程和科研分析的可靠性,且为后续RMC程序用于工程上的临界安全分析提供了数据支持。