从“算术”到“代数”的一次教学实践与探索
——以《用含有字母的式子表示稍复杂的数量关系和公式》教学为例
2023-03-11于元元
文|于元元
【教学内容】
苏教版五年级上册第101、102 页,练习十八第4、5 题,拓展习题。
【教学过程】
一、创设情境,提出问题
导入:同学们,苗族是一个非常有魅力的民族,他们拥有自己独特的文化和传统,并且一直在通过各种方式进行着传承和传播。今天让我们借助互联网云游苗寨,感受苗族的风土人情(边讲边播放“苗寨庆丰收举行长桌宴”的视频)。“长桌宴”是苗族宴席的最高形式与隆重礼仪,已有几千年的悠久历史。
师:视频看完了,关于“长桌宴”还有很多的数学知识(课件先出示“长桌宴”的场景图再出示“长桌宴”几何图),一起来探究吧。

【设计意图:笔者选择利用“苗族长桌宴的视频”导入,有三点想法:一是创设生活化的情境,有助于培养学生的应用意识,激发学生的兴趣;二是利用几何直观来培养学生的符号意识和建模思想;三是根据对教材中例4 的设计意图的理解,笔者对教材的“例4”进行了加工。】
二、寻找规律,探究新知
1.探究改编例题(例4)。
(1)出示题目。
课件依次出示:

提问:4 表示什么?2 表示什么?4+2 表示什么?
出示增加2 张桌子的图片。
提问:你又发现了什么?
预设:又增加了1 张或者一共2 张。

(随着学生的回答,补充式子)
师:如果增加3 张桌子,共坐多少人?你能写出表达“共坐的人数”的式子吗?你是怎样想的?
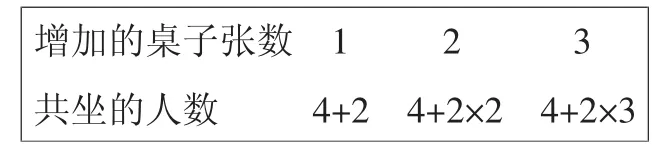
(2)完善表格,明确关系。

增加的桌子张数123共坐的人数4+2 4+2×2 4+2×3
引导学生观察生成的表格,讨论:增加的桌子张数和共坐的人数之间是什么关系?
明确:每增加一张桌子,就要增加2 人;增加几张桌子,共坐的人数就是4 加几个2 的和。这就是增加的桌子张数和共坐的人数之间的关系。
师:如果增加5 张方桌,你们会表示共坐人数的式子吗?如果增加10 张、20 张、30 张呢?
(学生口答即可)
师:现在增加的桌子数不知道具体有几张了,取而代之的是字母a,现在你还会表示共坐的人数吗?学生回答后教师出示完善后的表格并板书。
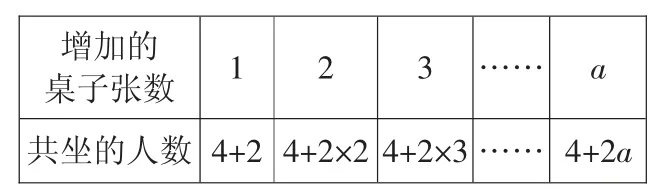
增加的桌子张数12 3共坐的人数4+2 4+2×24+2×3…… a…… 4+2a
板书:4+2×a(提问:2×a 表示什么?),有更简单的写法吗?(4+2a)
【设计意图:只有当学生对于数量关系熟悉之后,用算术表达稳定的情况下,再呈现另一种“代数”思想的表达,两种表达便不会混淆,反而会因为“代数”思想的来临让算术思维变得更加深刻而自然。】
(3)小结概括,引出课题。
概括:4+2a 不仅可以表示共坐的人数,还可以表示复杂的数量关系,这就是我们今天学习的“用含有字母的式子表示稍复杂的数量关系”(先板书课题中的一部分,后续再逐渐完善)。
提问:这里的a 可以是什么数?(铺垫:在具体情境中,字母表示的数是有范围的)
师:如果a=8,共坐多少人?如果a=15 呢?(口头代入求值)
【设计意图:通过这个环节引导学生理解,如果已经知道式子中的一个量,就可以通过运算得到另外一个量,从而进一步感悟可以用字母表示数量关系,让学生初步经历通过具体数值的计算归纳一般关系的过程。】
2.探究例5。
师:苗家人非常好客,给游客们准备了橙汁,看看这里又有什么数学问题等着我们来探究。
(1)课件出示例5。

提问:同学们,你们明白图的意思吗?谁来说一说它想要表达的数学信息?
交流后明确:冷水壶里有1100 毫升橙汁,倒了3 杯,每杯x毫升,还剩下一些。
(2)用字母表示数量关系。
师:你能用一个式子表示“冷水壶里还剩多少毫升橙汁吗?”谁来说一说?
预设:1100-x-x-x、1100-(x+x+x)、1100-3x。
(3)引导比较。
师:这些式子都能表示剩下的橙汁吗?它们有什么相同和不同?
小结:总量-已经倒出的量=剩下的量。
师:同样的数量关系可以用不同的式子来表示,哪个更简洁?
讨论:这里的x 可以表示哪些数?(再次感知:在具体情境中,字母表示的数有一定的范围)
小结:在具体的情境中,字母表示的数总是有一定范围的。
(4)自主学习“代入求值”的书写格式。
提问:根据你们研究得出的“1100-3x”这个式子,如果告诉你x=250 时,你知道怎样求冷水壶里还剩下多少毫升橙汁吗?
师:请同学们打开课本第101页,自学例5。
反馈收获:通过刚才的认真阅读,你学到了什么?
小结:字母表示的是数,结果不用带单位;将数值代入字母式,请注意书写格式。(等号对齐、运算顺序)
(学生板演“代入求值”的书写过程,再次强调基本方法和书写格式)
学生自主小结(教师根据情况进行完善):当告诉我们式子中字母的具体数值时,就可以把数代入式子,根据运算顺序计算出结果,但是一定要注意书写格式。
3.探究例6。
师:现在,让我们继续苗寨之旅,参观苗寨典型的建筑——吊脚楼,这是吊脚楼的缩小平面图(课件演示从吊脚楼实物图片中抽象出几何图形的过程),它的顶部图形是三角形。(课件出示例6的三角形图片)
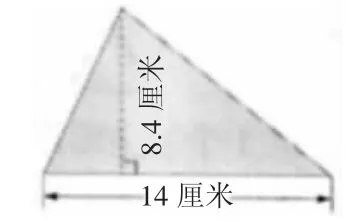
提问:三角形的面积计算公式是什么?用含有字母的式子怎样表示?(学生自主尝试)
活动要求:
1.平面图的底是14 厘米,高是8.4 厘米,这个三角形的面积是多少?
2.请你先写出计算公式,再把数值代入公式计算。
3.学生完成后指名板演,集体订正。
(课件出示计算过程)
提问:和老师的一样吗?同桌互相检查,看看哪里不一样,如果有错误请你帮他指出来,最好的学习方法就是教会他人。
小结:通过这道题的学习,我们知道含有字母的式子不仅表示数量关系,还可以表示计算公式,但我们需要注意的是:字母表示的是数,这里的计算结果也表示数,所以得数后不用写单位。
三、练习应用,巩固新知
1.完成“练一练”第1 题。
读题,明确题意后在表格内填写剩下的千克数。
交流引导:汇报填写的结果。说说你是怎样填写的。
提问:a-300b 表示什么意思?如果学生回答是剩下的千克数,可以追问学生还可以表示什么?
指出:用含有字母的式子表示数量关系时,就像写算式一样去思考,只不过是把字母看作一个数,按照题目的意思写出含有字母的式子即可。
2.完成“练一练”第3 题。这里是教材中第一次呈现长方形周长的字母公式,要求学生把它的周长公式规范地写下来,注意提醒学生C=2(a+b)中数字2 要写在括号的前面。
3.练习十八的第4、5 题,用智慧功能课堂做成内置选择题,推送给全班作答,利用数据精准定位教学,分析学生的失误原因,相机进行学习,进而突破障碍。
四、回顾反思,总结课堂
师:同学们,我们习惯一直向前跑,其实还应该学会驻足回望,看看我们走过的足迹,有哪些反思和收获,汲取了哪些经验,现在我们一起回望走过的足迹。
师:以后我们还会学到很多代数的知识,老师希望大家都能像数学家韦达一样,做一个勤于思考、勇于探索的人,做一个善于用数学知识和思维去解决问题的人。
【设计意图:课堂小结不仅要着眼于知识,还要着眼于获取知识过程中的收获和体会,突出学生探索过程的意义和价值。曹培英老师说:“教师有意渗透解决问题的思想方法是重于知识本身的。”】
五、反馈应用,设置作业
拓展题:
1.随着乡村振兴事业的发展,来苗寨旅行的人越来越多,根据我们发现的规律,如果有100 人参加长桌宴,你知道需要多少张方桌拼成一行长桌吗?

增加的桌子张数12 3共坐的人数4+2 4+2×24+2×3…… a…… 4+2a
2.思考:如果一共有a 张方桌,你能找到表达长桌共坐人数的另外一种含有字母的式子吗?

【设计意图:小学生数学建模思想的培养,可以充分利用几何直观,在交流过程中对学生进行语言能力的培养。通过示意图,学生可以得到很多变式的数量关系。例如:总人数=方桌一共的张数×2+4,方桌一共的张数=(总人数-4)÷2等,此环节试图通过现实情境和几何直观来激发学生生活经验与视觉观察能力,达到数学建模和符号意识双重培养的目的。】
