渗透数学思想 培育核心素养——《数学广角——集合》教学设计

文|朱 欢

【教学内容】

人教版三年级上册第104 页及相关练习。

【教学过程】

一、创设情境，激趣导入

课件出示：两对父子一起去理发，每人都要理，可是理发师只理了3 个人，这是为什么？

生：因为他们3 个人是爷爷、爸爸和儿子。

师：两个爸爸指的是谁和谁？两个儿子呢？

生：两个爸爸指的是爷爷和爸爸，两个儿子指的是爸爸和儿子。

课件出示：

师：是的，左边两人是儿子，右边两人是爸爸，中间的这位具有两个身份，他既是儿子的爸爸又是爷爷的儿子。在生活中像这样的重叠现象还有很多，这节课我们就来研究重叠问题——集合。

（板书：集合）

二、经历过程，探索新知

1.创设情境，引出问题

师：每年咱们都会举行秋季运动会，一起来看看三（1）班同学参加跳绳和踢毽子的人数吧。

课件出示：参加跳绳的有6人，踢毽子的有5 人。

师：能提出一个什么问题？

生：参加跳绳和踢毽子的一共有多少人？

师：怎么列式？

生：6+5=11（人）。

［板书：6+5=11（人）］

师：一定是11 人吗？

生：不一定是11 人。

师：为什么不一定是11 人呢？

生：可能有人两项活动都参加了。

2.操作验证，初悟重复

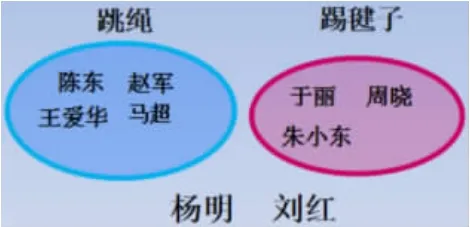
师：我们一起来看一看具体参加跳绳和踢毽子的学生名单。

跳绳 杨明 陈东 刘红 赵军王爱华马超踢毽子刘红 于丽 周晓杨明 朱小东

师：观察名单，有什么发现？

生：有人两项活动都参加了。

师：他们分别是谁？

生：杨明和刘红两项活动都参加了。

师：怎样才能清楚地看出哪些同学参加了两项比赛呢？

生：可以把两项比赛都参加的同学用线连起来。

跳绳 杨明 陈东 刘红 赵军王爱华马超踢毽子刘红 于丽 周晓 杨明朱小东

师：这样就能很清楚地看到两项活动都参加的同学，现在我们还能用6+5=11 这个算式来计算总人数吗？

生：不能。

师：那该怎么列式？

生：11-2=9（人）。

［板书：11-2=9（人）］

师：为什么要减2 呢？

生：因为杨明和刘红两项比赛都参加了，所以要减2。

3.游戏探究，感悟重复

师：为了把这种重复的现象更清晰地表示出来，我们借助摆一摆活动来看一看。

摆一摆的规则：

（1）同桌两人从信封里拿出参赛的名单比赛摆一摆，左边的同学负责摆好参加跳绳的6 人，右边的同学负责摆好参加踢毽子的5 人。

（2）准确快速地摆好的一方获胜，获胜方立即举手。

（教师巡视指导并在黑板上放好两个不同颜色的圆圈）

（学生在黑板上摆一摆，当摆杨明和刘红两位同学的位置时，遇到了困难）

师：遇到什么困难了？

生：不知道把杨明和刘红摆在哪个圈内？好像摆哪个圈内都不对。

师：为什么会出现这样的情况呢？

生：因为杨明和刘红两项比赛都参加了。

师：怎么才能让杨明和刘红既在跳绳圈内又在踢毽子圈内？

生：把这两个圈重叠起来，让他们两个人站到中间去。

师：老师能采访一下同学吗？你觉得这个方法怎么样？

生：这个方法好。把参加比赛的人分为三部分：只参加跳绳的、既参加跳绳的又参加踢毽子的、只参加踢毽子的。

师：像这样的两个圈数学上称它为集合，集合圈在数学上叫作韦恩图，谁再来说一说中间的部分表示的是什么？有几人？左边的部分表示的是什么？有几人？右边的部分表示的是什么？有几人？

师：关于表格和韦恩图，你觉得哪一个表示的方法更好？

生：韦恩图更好，因为韦恩图可以清晰地表示各部分的人数。

4.借助韦恩图，解决问题

师：既然韦恩图能够向我们传递这么多信息，那么你们能对照韦恩图来计算参加跳绳和踢毽子的一共有多少人吗？请列式解答。

展示学生的作品：

第一种情况：6+5-2=9（人）

第二种情况：4+2+3=9（人）

第三种情况：6+3=9（人）

第四种情况：4+5=9（人）

生：6+5-2=9（人）这个算式中，“5”是参加踢毽子比赛的人数，“6”是参加跳绳的人数，但有2位同学两项都参加了，多算了一遍，所以要“-2”。一共有9 人参加了这两项比赛。

生：4+2+3=9（人）这个算式中，“4”是只参加跳绳的人数，“2”是既参加跳绳的又参加踢毽子的人数，“3”是只参加踢毽子的人数，把它们加起来，一共就有9 人参加这两项比赛。

生：6+3=9（人）这个算式中，“6”是参加跳绳的人数，“3”是只参加踢毽子的人数，合起来就是一共有9 人参加这两项比赛。

生：4+5=9（人）这个算式中，“4”是只参加踢毽子的人数，“5”是参加跳绳的人数，合起来就是一共有9 人参加这两项比赛。

三、分层练习，巩固新知

1.基础训练

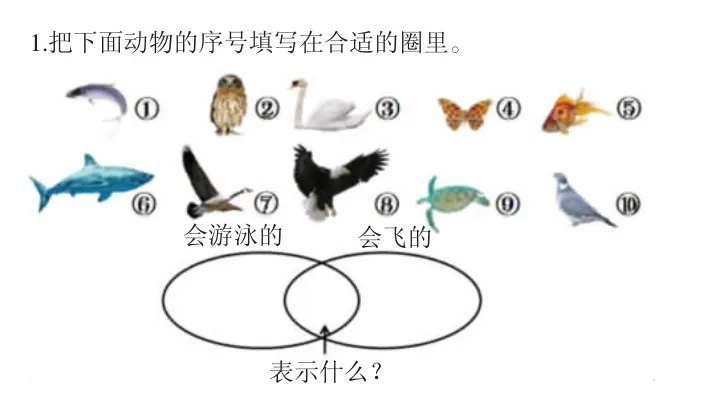
2.思维拓展

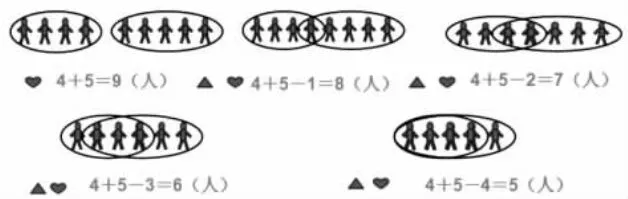
三年级（2）班如果有4 位同学喜欢画画，5 位同学喜欢唱歌，那么喜欢画画和唱歌的同学可能一共有多少位？

师：这道题和我们的例题比较，有什么不同？

生：喜欢画画和唱歌的学生可能重复，也可能不重复。重复的可能是1 人，也可能是2 人等多种情况。

师：请选择一种可能，用集合图和算式表示出你的想法。

（学生独立完成，教师巡视指导，并让学生展示不同的算法，重点讨论第一种和第五种情况，引出空集和包含这两种特殊情况）

四、课堂小结，拓展延伸

师：今天你有什么收获呢？