单元视角下多边形面积教学路径新探索——“多边形面积”单元教学内容分析与关键课例课堂实录

文|沈 强

一、单元教材分析

（一）依据图形之间的联系安排教学顺序，进行面积公式推导

翻阅国内各个版本的小学数学教材，多边形面积单元教学的顺序都是按先学“平行四边形面积”，再学“三角形面积”，最后学“梯形的面积”。平行四边形面积计算主要有两种方法，一种是直接度量，另一种是间接度量。直接度量是将平行四边形放在格子图中，通过数格子直接数出面积。间接度量是将平行四边形通过剪拼转化成长方形，利用长方形面积公式推导出平行四边形面积公式。三角形面积公式推导则主要采用倍拼法，用两个完全相同的三角形拼成一个平行四边形，利用平行四边形面积公式推导出三角形面积公式。教材还在“你知道吗”栏目中介绍《九章算术》中的“方田章”，详细论述平面图形面积的算法。而梯形面积公式的推导方法与三角形相似，也采用倍拼法。教材又在“你知道吗”栏目中介绍数学家刘徽利用出入相补原理来计算平面图形的面积。

（二）通过计算组合图形和不规则图形面积，培养解题思路和估测能力

在组合图形面积计算中，将其分解成若干个基本图形的能力是最基本能力，在保证数据完整性的多种分法中选取较优方法是较高能力。在计算组合图形面积中，既要保证学生达到基本能力，又要努力促进学生较高能力的发展。

在实际生活中，经常会测量各种不规则图形，它们往往无法分解成基本图形。学生需要根据图形的形状，灵活运用各种策略和方法估计出图形的面积，以提高估测能力和解决问题的能力。

二、单元课时划分

（一）教材中多边形面积公式推导方法较为单一

从教材编写来看，平行四边形面积公式推导采用剪拼法，三角形和梯形面积公式推导采用倍拼法，其他推导方法只作为课后简单了解，推导方法显得比较单一。

（二）学生较难自发联想到剪拼法和倍拼法

在平行四边形面积公式推导中，受长方形面积公式和四边形活动框架的影响，学生很容易想到面积是“邻边相乘”。且在学生心目中，学具是不能随意破坏的，学生不敢随意去剪平行四边形的纸片进行拼搭，较难自主联想到剪拼法。同样，三角形（或梯形）面积公式推导，如果只提供一个三角形（或梯形），学生是较难联想到用倍拼法来进行推导的。在实际课堂教学中，教师经常会提供多个完全相同的三角形或梯形，学生在随意拼搭中拼成已学过的平行四边形，所以倍拼法受学具的暗示性较强。

提出设想：能否将三角形面积公式推导作为单元起始课？

笔者一直在思考：若没有平行四边形面积公式的支撑，只学习长方形面积公式，三角形面积公式可否进行推导？学生会把三角形面积转化成什么图形来推导？学生如何想到把三角形面积转化成长方形面积？带着这些问题进行教学尝试，希望能另辟一条教学新路径。那么如果将之作为单元起始课，会有什么优势？从理论上来讲，三角形是最基本的图形，平行四边形和梯形都可将其分割成两个三角形进行公式推导，其他多边形也都能分割成若干个三角形进行面积公式推导。也就是说最基本图形的面积公式已知后，所有的多边形（包括圆形）都能借助基本图形进行面积公式推导。

基于以上的分析和思考，对本单元的教学顺序进行重构。单元重构着重体现两点想法：一是把三角形面积作为单元起始课；二是将平行四边形和梯形面积整合为一课时，因为这两个面积公式推导具有很强的相似性，既可以分割成两个三角形，利用乘法分配律进行推导，梯形又可以通过倍拼法转化成平行四边形。图1是整合后的单元编排结构图。

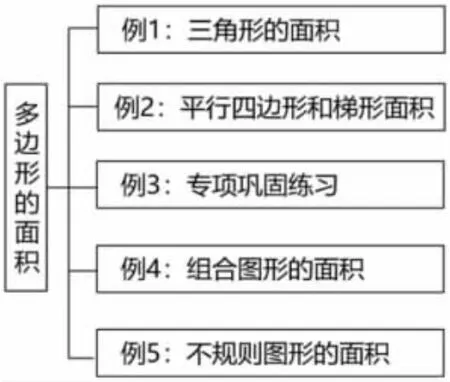
图1

图2

图3

三、关键课例设计

【第1 课时：三角形的面积】

（一）总体框架（表1）

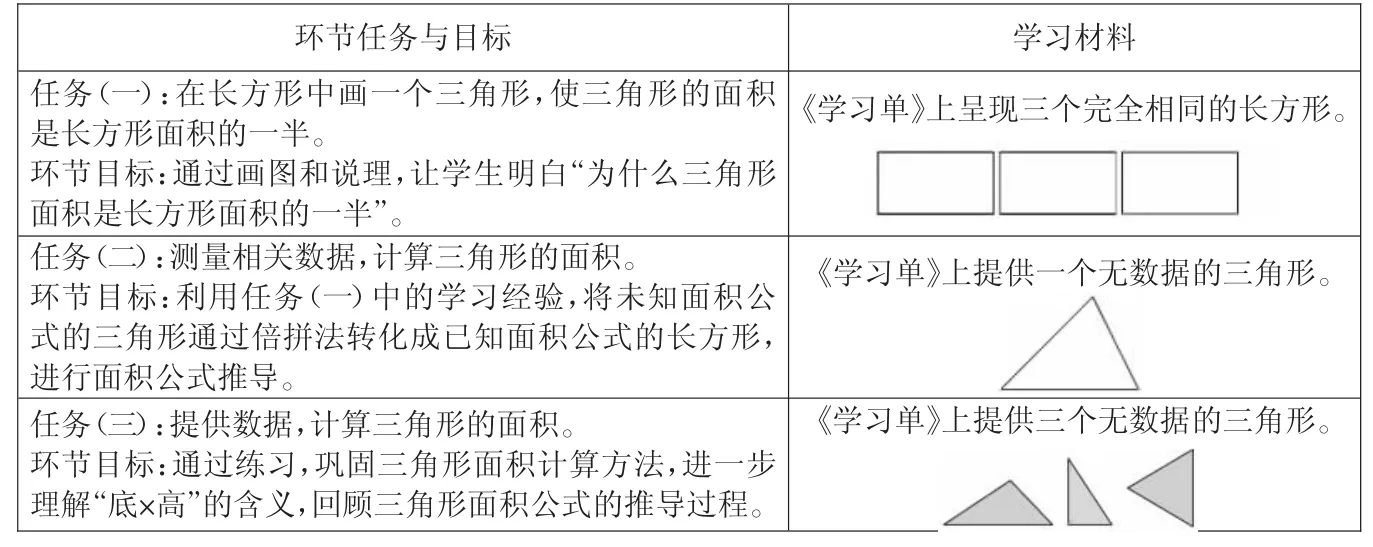
表1

（二）教学实录

●学习任务（一）：画三角形，使三角形面积是长方形面积的一半

1.呈现任务，尝试画图

提出任务：在长方形里画一个三角形，使三角形面积是长方形面积的一半。呈现学生的作品。

师：你有什么办法说明三角形面积是长方形面积的一半？

生：可以沿着长方形对角线剪开，将两个三角形叠在一起，看看是不是一样大。

学生动手操作，得出结论：沿着长方形的对角线剪开，两个三角形的面积一样大。

2.多元表征，表达画法

师：你还能画出不一样的三角形吗？

学生动手操作，组内交流。呈现学生的作品。

师：说一说你是怎么画的？

生：图4 先在长方形的上边找到中点，再画一个三角形。

图4

生：图5 在长方形上边任意找一个点，然后画一个三角形。

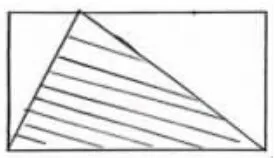
图5

3.引出高线，便于说理

师：关于图4 你有什么办法说明三角形面积是长方形面积的一半？

生：可以在三角形的中间添上一条线。

让学生上台，在三角形中添线（如图6 不出示①②③④），教师追问：这条线画的时候有什么要求？

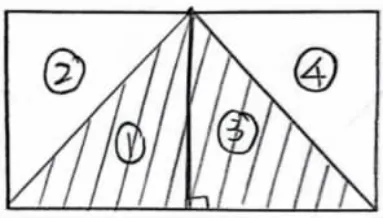
图6

生：这条线要与下面的边互相垂直。

师：你发现所画的这条线就是三角形的什么？

生：三角形的高。

师：继续说一说你的想法。

生：我把四个三角形标一下，①号和②号面积相等，③号和④号面积相等，所以三角形面积是长方形面积的一半。

师：你们发现要说清楚，必须做什么？

生：必须画高。

对于图5，让学生添上高线后互相说一说。

●学习任务（二）：量出数据，计算三角形的面积

1.提出问题，尝试解决

呈现《学习单》上的三角形，提出任务：测量边线的长度，计算出三角形的面积。

2.呈现作品，反馈交流

呈现作品1：只测量三条边线的长度（如图7）。

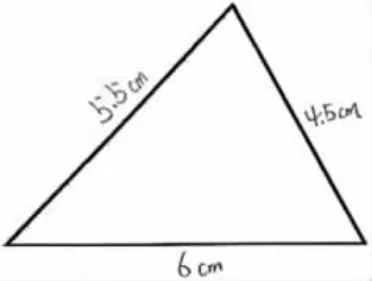
图7

师：你是怎么想的？遇到了什么困难？

生：我想三角形的面积应该跟三条边的长度有关，但测量出长度后就不知道怎么做了。

呈现作品2：计算三角形的周长。

师：你们看懂这位同学是怎么做的了吗？

生：他算的是三角形的周长，而我们要求三角形的面积，所以不对。

呈现作品3：利用面积公式计算（如图8）。

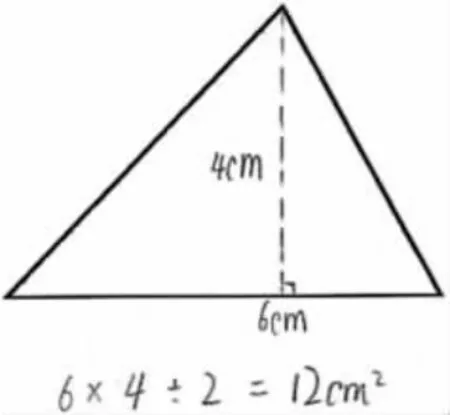
图8

师：你是怎么想的？

生：我测量了三角形的底和高，利用三角形面积=底×高÷2，算出来是6×4÷2=12（cm2）。

师：原来你已经知道了三角形面积的计算方法，那你知道为什么这么算吗？

生：我看了书上的公式，但不清楚为什么要这样算。

呈现学生作品4：利用长方形和三角形之间的面积关系来计算（如图9）。

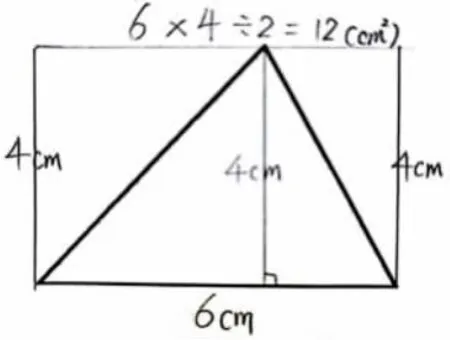
图9

师：有谁看懂他的方法了？

生：在三角形外面画了一个长方形，长是6cm，宽是4cm，所以长方形的面积是24cm2。刚才我们知道三角形的面积是长方形的一半，所以24 再除以2 等于12cm2。

生：他利用了任务（一）中的结论，先算出长方形面积，再除以2 就是三角形面积。

3.公式推导，得出结论

师：6×4÷2，谁来说一说这里的6 和4 分别表示什么意思？

生：6cm 是长方形的长，也是三角形的底。

生：4cm 既长方形的宽，又是三角形的高。

师：那你觉得三角形的面积公式可能怎么表达？

生：长方形面积÷2=三角形面积。

生：底×高÷2=三角形面积。

师：这两个公式都正确，你觉得以后用哪个公式更方便？

生：用下面的公式，因为我们推导的过程是用上面的公式，要求三角形的面积就要用三角形的底和高。

板书公式：底×高÷2=三角形面积。

●学习任务（三）：提供数据，巩固三角形面积计算方法

1.提供数据，列式计算

呈现3 个没有数据的三角形，思考：要计算三角形面积，你需要老师提供哪些数据？

生：需要知道底和高。

教师呈现底和高的数据（如图10），计算3 个三角形的面积。

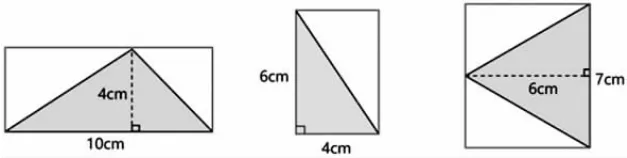
图10

生：10×4÷2=20（cm2），4×6÷2=12（cm2），7×6÷2=21（cm2）。

2.提出思考，回顾推导

师：请你想一想算式中的“10×4”“4×6”“7×6”分别是在算什么？你能把这个长方形画出来吗？

通过课堂实践，发现把三角形面积作为单元起始课是可行的，学生也能顺利地进行面积公式推导，并理解其中的道理。同时，将平行四边形和梯形面积公式推导放在“例2”，教学实践效果也较好。在“例3”专项巩固练习中，继续开展三角形、平行四边形和梯形面积其他的推导方法，丰富推导方法，满足不同层次学生的需求。在不断思考和教学实践中，找到了多边形面积教学的新路径，我们不比哪个学习路径更好，而是在单元视角下打开教学研究的一种思路，提升研究能力和实践能力。