基于分组优化改进粒子群算法的无人机三维路径规划*

蔺文轩，谢文俊，张 鹏，纪良杰

（1.空军工程大学研究生院，西安 710043；2.空军工程大学装备管理与无人机工程学院，西安 710043）

0 引言

近年来无人机凭借其优异的性能在战争中崭露头角，表现出极强的战斗力，成为一种新兴的作战力量，无人机能否成功、高效地完成作战任务，路径规划起到了至关重要的作用。针对无人机路径规划问题，目前研究成果较多，主要的研究算法有遗传算法［1］、蚁群算法［2］、A*算法［3］、人工势场法［4］、粒子群算法［5］等。岳秀等人针对多无人机多目标分配问题，首先采用A*算法对无人机进行了最优路径的求解，再将多目标分解为多个子目标，利用改进的模拟退火算法针对子目标进行航迹规划，实现了无人机巡航状态下对子目标区域的高覆盖［6］。贾会群等针对使用传统粒子群算法对机器人进行路径规划时出现的搜索滞留的缺点，向算法中引入鸡群优化算法中的母鸡和小鸡更新策略，对停滞粒子进行扰动，提高了算法的全局搜索能力［7］。范叶满等针对植保无人机在丘陵山地区域工作效率低下的问题，以四旋翼无人机为例建立了相应的运动学模型，并通过模拟退火算法完成了无人机在山地作业情况下最优能耗的路径规划［8］。无人机路径规划需要考虑战场环境、目标威胁、自身条件等约束条件，实质上是一个典型的多目标优化问题［9］，粒子群算法凭借其算法简单、高效、运算迅速的特点广泛应用于寻优问题求解［10］，但其在求解无人机三维路径规划问题时存在易陷入局部极值、早熟、全局搜索能力较差等问题。本文以粒子群算法为基础，针对其缺点提出了一种基于鸡群分组优化策略的粒子群算法，通过对粒子进行分组提高粒子群算法的局部搜索能力，并采取模拟退火操作对粒子更新规则进行处理，在算法早期增加了粒子的多样性，能够有效避免粒子群算法易陷入局部极值和早熟的问题，并通过实验仿真验证了其在解决无人机三维路径规划问题上的可行性。

1 算法原理

1.1 粒子群算法

粒子群算法通过模拟鸟类的捕食现象，利用群体中个体信息的共享，使得整个群体在求解空间中实现从无序到有序的过程，并寻得最优解。算法的主要内容为：假设在D 维搜索空间中，存在种群数量为N 的粒子群，每个粒子的位置及速度分别表示为Xi={Xi1，Xi2，…，Xin}，Vi={Vi1，Vi2，…，Vin}，每一个粒子的最优解Pbest表示为Pi={Pi1，Pi2，…，Pin}，全局最优解Gbest表示为Pg={Pg1，Pg2，…，Pgn}，粒子群中的每个粒子根据Pbest和Gbest更新自己的位置和速度，具体方法为：

式中，t 表示当前迭代次数；Pid表示当前更新粒子最优解，Pgd表示当前全局最优解；c1，c2为学习因子，主要控制粒子根据现有信息进行判断，对自身位置进行调整，向潜在最优位置移动；r1，r2为［0，1］上的随机数。

1.2 鸡群优化算法

鸡群算法［11］（chicken swarm optimization，CSO）是一种模拟鸡群觅食行为的仿真算法，根据鸡群内的等级制度对粒子进行分类，能够有效地解决智能算法常见的早熟现象，且具有收敛速度快，寻优能力强的特点。其算法原理如下：

鸡群在觅食过程中根据公鸡的数量进行分组，小组内的公鸡在组内具有领导作用，母鸡的觅食线路受限于公鸡，小鸡的觅食线路受限于母鸡。在算法初期根据粒子个体的适应度差异对粒子进行分组，根据适应度的好坏将粒子依次分为公鸡、母鸡、小鸡。

公鸡的适应度最好，具有最大的搜索范围负责全局搜索，其位置更新规则如下：

母鸡跟随公鸡的觅食路线，其位置更新策略如下：

式中，k1为母鸡所在小组内公鸡对其的影响因子；k2为其他鸡对其的影响因子；rand 表示［0，1］的随机数；r1表示母鸡跟随的攻击；r2表示任意小组的公鸡或母鸡。

小鸡跟随母鸡的觅食路线，其位置更新策略入下：

式中，m 表示当前小鸡i 跟随的母鸡，FL 表示［0，2］上的随机数。

2 基于分组优化的粒子群算法设计

2.1 鸡群算法与粒子群算法对比

粒子群算法与鸡群算法的相同点：1）都是仿生智能算法；2）都是全局随机搜索算法；3）都容易陷入局部最优解；4）都选择适应度较好的个体作为更新标准；5）都受到先前经验的影响。

粒子群算法与鸡群算法的不同点：1）粒子群算法在运算过程中整体是一个种群，鸡群算法在进化过程中将鸡群分为若干小组，组内与组间进行信息交互与竞争；2）粒子群算法每个粒子都会存储最优适应度，鸡群算法中只有小组内的公鸡记录小组的最优解，其余成员根据公鸡位置进行位置更新；3）粒子群算法中每个个体的地位都是同级的，鸡群算法中将个体按照适应度进行了等级划分，适应度好的个体具有较强的搜索能力，适应度差的个体需要跟随适应度好的个体进行搜索。

通过对两种算法的对比发现其有很多相同之处，都强调个体的搜索功能，但在个体的等级划分上存在区别。在进行搜索的过程中，粒子群算法容易受到当前全局最优解的影响，容易陷入局部最优循环，导致算法性能下降。综合分析将两种算法结合，以鸡群分组更新策略改进粒子群迭代更新策略，避免算法陷入局部最优循环，提高全局搜索能力。

2.2 基于分组优化的粒子群算法设计

改进的算法描述为：在初始化过程中，根据鸡群算法的分组策略，选择适应度较好的粒子作为排头粒子，并将所有粒子分为n 组，将适应度较好的粒子作为小组内的最优粒子。根据鸡群算法原理，小组内的最优粒子能够搜索较大的目标区域，其余粒子主要在最优粒子的影响下进行局部区域的最优搜索，小组内的等级变化通过适应度的改变进行调整。经此改进，粒子群算法中的所有小组最优粒子负责全局空间的最优搜索；各小组内的粒子负责目标空间的局部搜索，提高算法的局部搜索能力。改进后小组的粒子更新规则如下：

1）最优粒子更新规则：

xij表示小组i 内的第j 个粒子，S1=exp（fi，j-fi，jd）/（abs（fi，j）+ε），S2=exp（fi，gd-fi，j），是改进后学习因子，fi，j表示当前粒子的适应度，pi，jd表示小组i 的最优粒子xi，j的最优解，pi，gd表示小组i 内处最优粒子外任一粒子的最优解。k 为该小组内最优粒子外的任一其他粒子。

2）小组内粒子更新规则：

式中，pid为小组内粒子的最优解；pgd为全部粒子的最优解。由式（8）易得，小组粒子更新速度几乎只受惯性权重ω 的影响，ω 的值随着迭代次数的增加逐渐减小，这就导致了小组内粒子更新的停滞，陷入局部最优解，为解决这一问题，在小组粒子进行局部搜索时加入模拟退火操作，增加小组粒子的多样性，进一步提高小组粒子的局部搜索能力。

模拟退火算法的基本原理为：当固体温度较高时，粒子区域无序；当温度降低时，粒子逐渐趋于稳定［12-13］。当固体具有一定的温度时，算法具有绝对收敛到全局极值的能力，采用Metropolis 准则［14］进行算法更新，如下式所示：

设初始粒子数量为N，最大迭代次数为T，根据初始适应度确定分组数量为n，具体的算法流程如下：

Step 1：初始化算法，设定各参数值；

Step 2：计算每个粒子的适应度，根据适应度将粒子分为n 组，确定小组最优粒子；

Step 3：初始化小组最优粒子、全局最优粒子、模拟退火温度；

Step 4：判断是否符合终止条件。若符合条件输出最优规划路径，否则执行Step 5；

Step 5：计算粒子适应度fi（t），更新小组最优解和全局最优解；

Step 6：更新粒子速度和位置；根据式（7）、式（8）更新小组最优粒子速度和位置，根据式（10）、式（11）更新小组内其他粒子速度和位置；

Step 7：计算各粒子更新后的适应度fi（t+1）和适应度变化量Δf；

Step 8：根据式（12）判断是否接受粒子更新后的速度和位置；

Step 9：进行模拟退火操作，并跳转Step 4；

改进后的算法流程图如图1 所示。

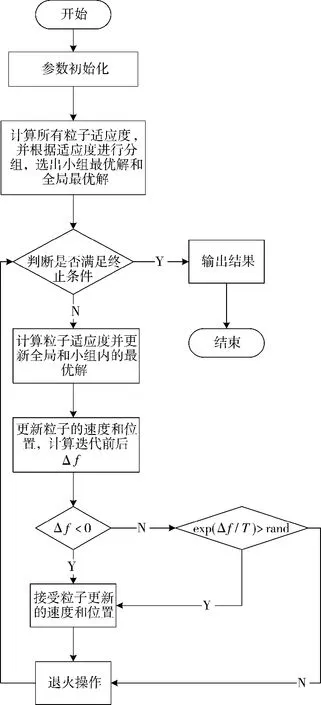
图1 基于鸡群分组策略的粒子群算法流程图Fig.1 Flow chart of particle swarm algorithm based on chicken swarm grouping strategy

3 无人机航迹规划代价函数

3.1 航程代价

航程代价主要指无人机在飞行过程中的燃油消耗，假设无人机在执行任务过程中达到规划速度后保持匀速飞行，故燃油消耗量与无人机的总航程成正比，航程代价表示如下：

其中，ε 表示单位航程的燃油消耗量；Qv表示无人机所携带的燃油总量；Li表示第i 段航迹的长度。

3.2 飞行高度代价

无人机在飞行过程中，被敌方雷达探测到的概率与其飞行高度成正比，受地形威胁的概率与飞行高度成反比，为了提高无人机的生存概率，设定最高飞行高度Hmax和最低飞行高度Hmin，设当前飞行高度为Hi，飞行高度代价函数表示如下：

3.3 威胁代价

受环境地形、禁飞区、防空火力等的影响，无人机航迹规划时需考虑环境的威胁代价，设在规划的第i 段航迹无人机接近威胁点k，将当前航迹段Li分割成m 小段，则威胁点k 对航迹段Li的威胁代价函数表示如下：

式中，ni表示航迹规划中的第i 段航迹Li；Pk表示第k 个威胁点的对无人机的毁伤概率；dm，k表示第k 个威胁点到航迹段Li中第m 小段的距离。

无人机航迹规划受到的总威胁代价为：

3.4 多无人机协同航迹规划收益函数

4 实验仿真及结果分析

4.1 实验仿真

为验证本文设计算法的可行性，使用Matlab 软件对无人机三维路径规划进行实验仿真。本次仿真地图大小设置为：100 km*150 km*30 km，起飞点坐标为（10，90），目标点坐标为（130，10）。威胁区域的二维坐标参数如下页表1 所示。

表1 威胁区域二维坐标参数Table 1 2-D coordinate parameters of threat area

对威胁区域建模，使用粉色部分表示威胁区域，如图2 所示。

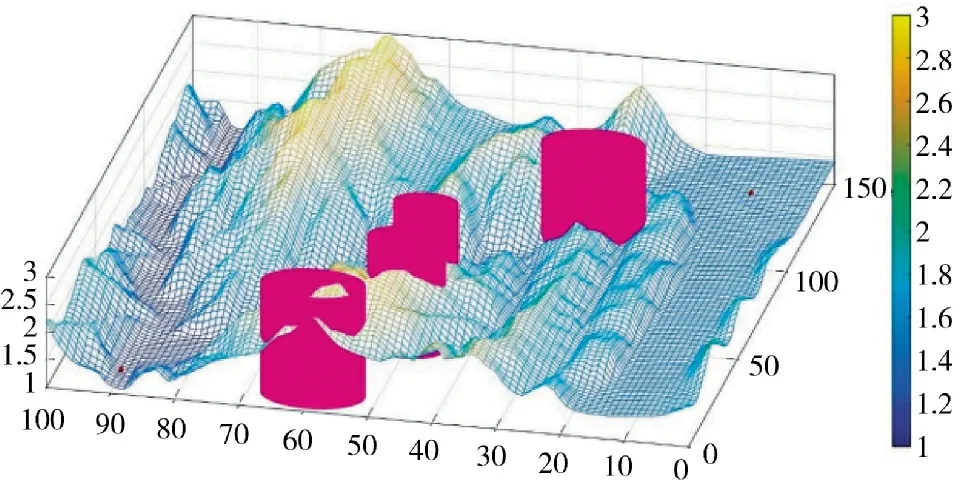
图2 三维威胁地形图Fig.2 Three-dimensional threat topographic map

使用标准粒子群算法对上述问题进行三维路径规划求解作为参考，其参数设置为：粒子数量N=30，最大迭代次数T=200，学习因子c1=c2=2，惯性权重ω=1，退化率为0.99。

仿真结果如图3～图5 所示。

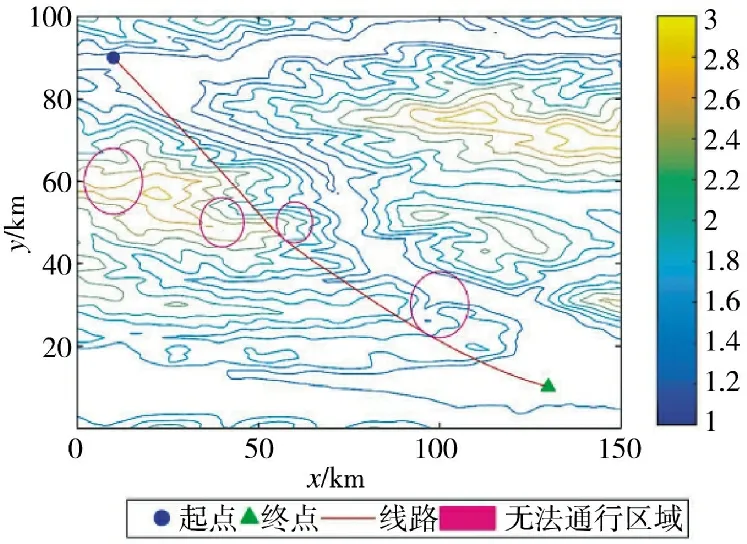
图3 二维航迹规划图Fig.3 Two-dimensional route planning diagram

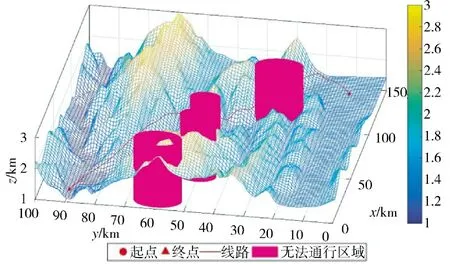
图4 三维航迹规划图Fig.4 3D route planning diagram

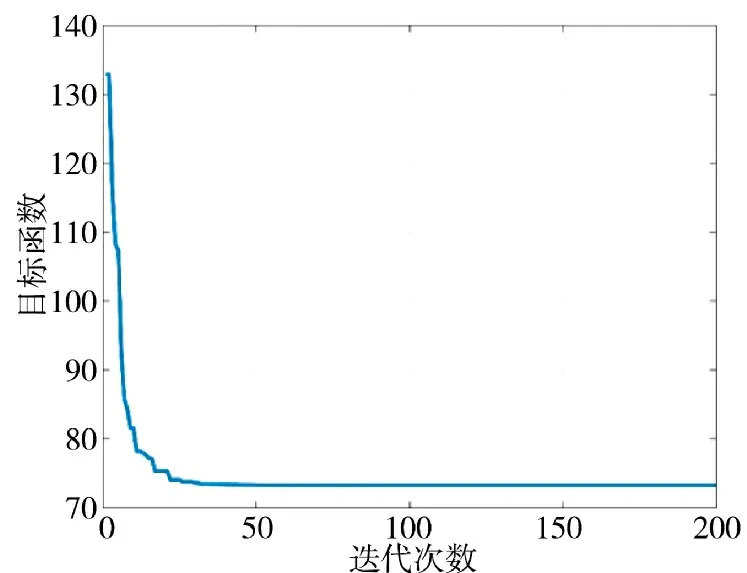
图5 适应度变化曲线Fig.5 Fitness change curve

优化后的粒子群算法的参数设置为：粒子数量、最大迭代次数、学习因子、惯性权重取值、退化率均不变，小组数量为5，模拟退火初始温度为400，温度衰减系数为0.99。在对标准粒子群算法增加了鸡群分组策略和模拟退火操作后的实验仿真结果如图6～图8 所示。

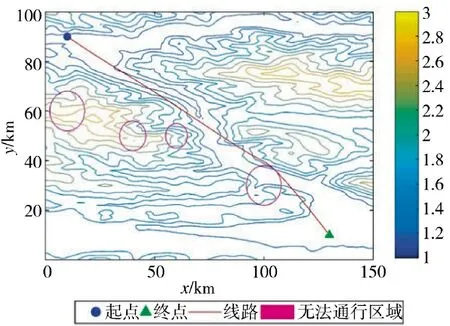
图6 改进后的二维航迹规划图Fig.6 Improved 2D route planning diagram

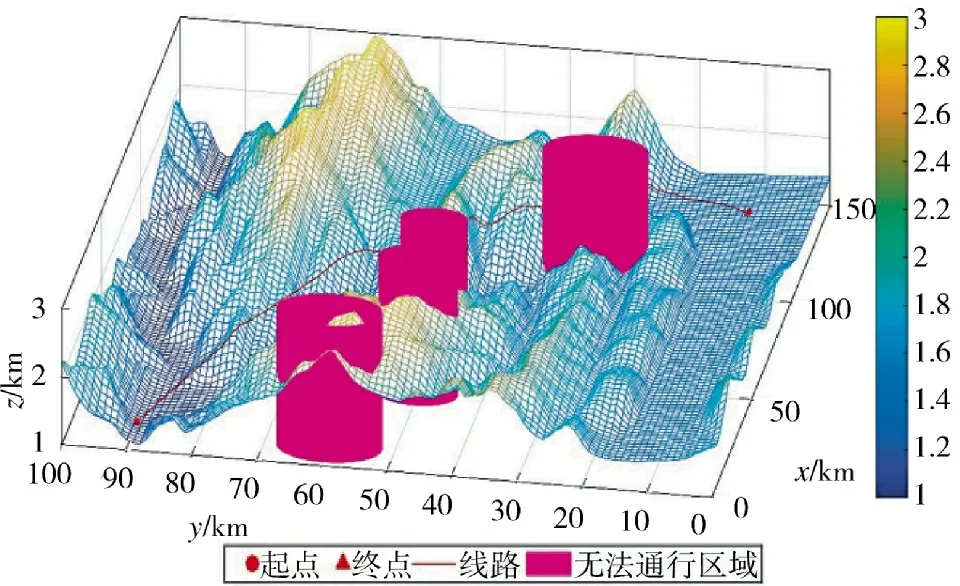
图7 改进后的三维航迹规划图Fig.7 Improved 3D route planning diagram

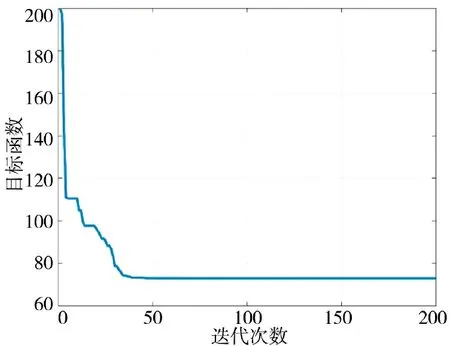
图8 改进后的适应度变化曲线Fig.8 Fitness change curve after improvement

4.2 仿真结果分析

针对两次实验结果进行分析，可以看出标准粒子群算法规划出的航线从两个威胁区域之间穿过，这种方式有较大的风险隐患，容易被侦察探测到。改进后的粒子群算法则避免了这种问题，最大程度规避了威胁区域，降低了执行任务的风险，同时改进后的粒子群算法规划的航迹飞行高度较低，更加贴近山体飞行，能够大幅降低被敌方地面雷达探测到的概率。根据适应度曲线的变化可以看出，改进后的粒子群算法迭代次数更多，迭代初期的目标函数值更高，最后收敛的目标函数值几乎相同，这表明改进后的算法搜索了更大的范围，在全局搜索能力上更强。综合考虑，改进后的粒子群算法规划的无人机航迹更好，验证了算法改进的有效性。

在相同的环境下，分别用两组算法进行30 次的独立仿真，对两种算法的综合代价模型进行统计，统计结果如表2 所示。

表2 实验结果统计Table 2 Statistics of experimental results

对两组实验结果易知，两种算法对无人机航迹进行规划时，最优代价相差不大，但是标准粒子群算法的平均代价及标准差都不如改进后的算法优秀，这表明使用改进的粒子群算法进行航迹规划时寻优的稳定性更好；改进的粒子群算法的平均迭代次数明显高于标准粒子群算法，表明改进后的算法搜索的范围更广，全局搜索能力更强；虽然改进后的算法在平均运算耗时上有所增加，但时间相差不大，总体来看，改进后的算法更加适用于无人机的三维路径规划。

5 结论

本文针对无人机三维路径规划问题，设计了一种基于鸡群分组优化策略的粒子群优化算法，在改进的算法中加入了模拟退火操作，并通过仿真实验验证了改进后算法的可行性和有效性，相较于标准的粒子群算法，改进后的算法在全局搜索能力上更强，寻优的稳定性更高，对局部区域的搜索能力较高，能够有效地避免陷入局部最优、过早成熟等问题，规划的无人机航线更加合理，代价更优。