河道清淤工程淤积方量计算方法的对比研究与应用

廖 月 侯 煜 张劲军 张楚楚 杨艳慧

（江苏省泰州引江河管理处 泰州 225321）

1 引言

淤积方量的计算是目前河道清淤施工中最为重要的工作之一，不仅在前期对工程预算和施工方案的选择有重要的指导意义，还是施工结束工作量复核的重要依据。对于不同地形地貌，选择计算方法是不一样的，目前常用的淤积方量计算方法主要有断面法、DTM法、方格网法及等高线法四种。本文采用基于AutoCAD平台的南方CASS软件，探究四种计算方法原理及优劣，结合高港枢纽下游引水河道清淤工程实例，分析四种计算方法在实际应用中的精确度。

2 河道淤积方量计算方法的原理

2.1 断面法

断面法多应用于河道、沟渠、管道等狭长的条状地形，同时也适用于面状及有台有坎地形。在地形图或碎部测量的平面图上，以固定的间距等分土方的计算范围，将其划分成数个相互平行的横断面，按照现有断面线及设计断面线组成的断面图计算挖填面积，两个相邻横断面的平均面积与断面间距的乘积即为两断面间的挖填方量，将各段区域的值累加即可得到整个区域的挖填方量。

设横断面面积分别是S1，S2，S3……Sn；断面间距为H，则总的挖填方量为：

2.2 DTM法

数字地面模型（DigitalTerrainModel，DTM）是地貌形态的离散表示，用坐标（X,Y,Z）表达区域内的地貌形态。DTM法适用于计算复杂地貌至水平平面的挖填方量，根据实测地面点坐标（X,Y,Z）和设计高程，利用复合线划定挖填分界线，生成不规则三角网计算每个三棱锥的挖填方量，最后累加得到整个区域的挖填方量。另外也可对同一区域进行两期测量，通过两次测量得到的高程数据进行建模，计算出两期整个区域的土方变化，即可得到整个区域完成的土方挖填量。

设E、F、G为三角网的三个顶点，它们到设计高程的高差分别是h1、h2和h3；S为三棱锥的底面积，则总的挖填方量为：

2.3 方格网法

方格网法与DTM法前期工作基本一致，但适用于地形变化较小的区域。根据实测地面点坐标（X,Y,Z）和设计高程，先将待计算的区域生成若干个方格，再将方格的四个角上的高程相加，取平均值与设计高程相减，然后根据方格边长利用长方体体积计算公式得到每个方格的挖填方量，最后累计得到整个区域的挖填方量。

设方格网边长为a、b；hij表示第i行j列的方格网高差；n为测区方格的个数。总的挖填方量为：

2.4 等高线法

等高线法适用于等高线完全闭合区域，利用两条等高线围成的面积和高差来计算两条等高线之间的土方量。两条等高线之间的体积可以近似看作截锥体，先计算出两条等高线围成的面积，再利用两条等高线之间的高差，通过计算公式可以算出两条等高线所围的土方量。

设Sn、Sn-1为任意两条等高线的截椎体底面积；hn、hn-1为任意两条等高线的高程，则任意两条等高线的挖填方量为：

3 河道淤积方量计算方法的优劣对比

3.1 断面法

用断面法计算清淤方量，断面线的布置十分关键，必须遵循以下布设原则：①在平顺且河床地形变化不大的河道，河道断面可以平均布设，垂直于河道主流方向，距离可以适当调远；②当河道弯曲或河床地形变化较大的区域，应加密设置河道断面线，满足计算淤积量的精度要求；③在河道主流方向变化较大的区域，同样应加密布置河道断面线，使划分的各个区域断面线垂直于主流方向，以便于确定断面间距，确保计算清淤方量的准确度。

用断面法计算清淤方量，当断面布置较近时，虽然计算精度有保障，但外业测量及内业计算量较大；当断面布置较远时，虽然外业及内业工作相对减少，但精度较差。同时断面法必须对各断面的参数包括设计坡比、河底高程的设置比较清楚，鉴于断面法受到的诸多限制，在河道弯曲及河床地形变化较大时，计算精度和可靠性很难获得保证。

3.2 DTM法

DTM法从理论上讲能够适应各种地形地貌，通过测深仪采集河床特征点高程，所形成的三角网能直观地展现地形特征，同时可以将使用的高程点作为水下地形图高程点而无须重新测量，具有较高的计算精度。但DTM法在建模时通常比较复杂，需要软件进行辅助测量，同时需要大量的数据来确保建模的准确性，这就要求在使用DTM法时要尽可能采集更多的高程点，高程点的精度、密度和均匀性与计算结果息息相关。

3.3 方格网法

方格网法相对简明直观、通用性强，可以生成挖填线，但由于方格网法需要提取4个角上的高程来计算方格网的体积，有时角上没有高程点，需要利用其他高程点内插得到该处的高程点，同时图上等高线与实际地形有很大的差距，计算出的清淤方量必然也有很大的差距。只有地形越平缓，各个方格点的图上高程与实际高程越接近，计算结果才能越精确。

3.4 等高线法

等高线法在计算时精度较低，不但需要地形图，等高线还必须是闭合的，不适合河道清淤方量的计算，所以等高线法不在本文进行具体讨论。但在一些山头或盆地区域，等高线法是比较合适的方法。

4 河道淤积方量计算方法的工程验证

4.1 项目概况

高港枢纽是国家南水北调东线规划的水源工程之一，高港节制闸为中型水闸，由下游（长江侧）向上游引水。下游引水河道总长约2.0km左右，平均淤积在2～3m，淤积总方量超过50万m³。近年来，高港枢纽对下游引水河道进行了3期河道清淤施工，清淤总方量超过16万m³。

4.2 精度对比

为了验证3种计算方法的理论精度，本次采用断面法、DTM法及方格网法分别对河道平顺区（C.S.13-C.S.16断面，河床地形变化较小）及口门区域（C.S.22-C.S.24断面，河床地形变化较大）进行计算，比对其在不同河道条件下的精确度。

区域土方量平衡是以挖填边界线为界，计算出一个土方平衡高度，使挖方量等于填方量，可以通过区域土方量平衡法计算的结果来判断3种计算方法的精确度。根据区域土方量平衡计算，C.S.13-C.S.16断面平场面积设置为29269.3m2，土方平衡高度-3.096m；C.S.22-C.S.24断面平场面积设置为26440.6m2，土方平衡高度-2.458m。图1为区域平衡法图。

图1 区域平衡法图

在平场面积、采样间隔和平场高度都采取以上数值时，3种计算方法计算结果如表1、表2。

表1 C.S.13-C.S.16断面相对精度计算表

表2 C.S.22-C.S.24断面相对精度计算表

通过精度计算表可知，DTM法精度最高，计算结果是可信任的；方格网法次之，无论河道地形有何变化，方格网法的相对误差均在10%以内；而从结果看，断面法精度最低，在平顺及地形变化不大的河道误差在10%～15%，而在弯曲及地形变化较大的河道误差超过了25%。

4.3 清淤方量计算

通过与区域平衡法在两个区域的比较，发现DTM法在河道清淤方量的计算中精度最高，方格网次之，断面法精度最低。下面就以C.S.13-C.S.16断面两期数据为例，对比三种计算方法得到的数据误差。

4.3.1 断面法

应用断面法计算，该段河道标准断面的设计高程、坡比均已知，断面间距为50m。将两期数据分别生成里程文件，利用二断面线间土方计算法计算每个断面清淤前后横断面积变化，挖方量为15471.2m³，填方量为3253.3m³。

4.3.2 DTM法

应用DTM法分别对两期高程数据进行建模，计算出该区域的清淤方量。图2为DTM法图。深色部分表示高程发生变化，即此区域已进行了清淤施工。通过软件计算，得到挖方量为13918.5m³，填方量为1430.7m³。

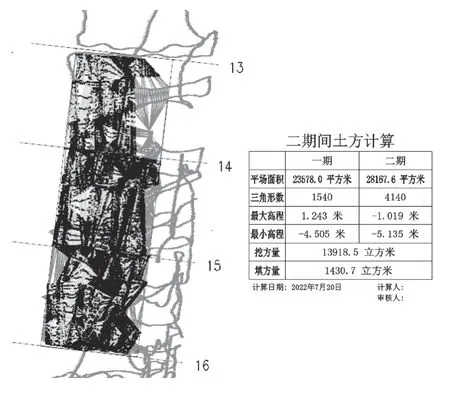
图2 DTM法图

4.3.3 方格网法

利用方格网法对相同的区域进行清淤方量计算，方格网法生成的网格以及各个网格自动生成的挖填方量较为利于组织施工。为了计算准确，将两期河底目标高程均设置为-4m，施工前挖方量为24551.1m³，填方量为500.3m³；施工后挖方量为11990.0m³，填方量为2881.0m³。施工后部分区域存在超挖，方量约为2380.7m³，实际的挖方量为14941.8m³。

4.3.4 计算结果对比

从计算结果显示，以DTM法13918.5m³为基值，方格网法误差7.35%，断面法误差11.16%。

5 结论

通过以上四种计算方法的对比以及实例研究可以得出：在河道清淤方量的计算中，DTM法在两期清淤土方的计算中具有无可比拟的精确度及速度优势，只要在外业中采集到足够的反应河床变化的高程数据，无论河床地形如何变化，DTM法都可以迅速地计算出清淤方量，不仅提高了工作效率，还可以为清淤工程的准确结算提供有力支撑，因此DTM法可以作为河道清淤方量计算的首选方法■