双层均质耦合网络信息传播动力学研究

罗章凯，裴忠民，熊 伟，刘 朦

(航天工程大学复杂电子系统仿真实验室，北京 101416)

1 引言

空间信息网络以网络化方法融合各类空天平台，形成一个综合复杂的网络系统，同时也是一个复杂网络信息系统，是进行信息支援的主要平台和进行态势感知的重要基础设施[1]。针对当前的空间信息网络，其实体多样性和连接互异性导致单层网络难以完全描述其结构功能特征。鉴于此，基于双层和多层网络结构对空间信息网络进行建模的方法被相继提出，如文献[2，3]根据空间实体物理位置不同，将空间信息网络中的实体节点分多层。文献[4]中提出基于3D-Mesh网络的体系结构，依据实体节点所处的层次和功能将空间信息网络划分为3个自治域，即骨干网络域、接入网络域和用户域，并分析了该结构的优势和基于此结构的空间信息网络协议架构模型。文献[37]针对空间信息的非均匀分布和邻近性特点，以及海量空间信息处理中逻辑覆盖网络与物理网络不一致的问题，引入对等网络(P2P)分层理论。将空间信息网络分为多层进行研究可以较好展现空间信息网络特征。

空间信息网络中各类空天平台和系统主要以无线通信方式互联互通，通信链路是否建立可以通过概率表示。基于图论理论可知[5]，空间信息网络中各类实体可以抽象为节点，节点之间是否联系可以抽象为是否有边相连，链路是否建立概率可以通过边的权重表示，从而可以将空间信息网络抽象构建为网络化拓扑结构模型。进而可以采用成熟的复杂网络理论和最新的智能技术对空间信息网络形成机制和内在机理进行分析和研究，包括空间信息网络的规划与设计、网络组网分析[6-8]和信息传播动力学[9-13]等研究。

当前对多层网络传播动力学研究已有部分研究成果，如文献[14]中以社会网络为背景研究传播动力学；文献[13]研究人类网络中传染病在多层网络中传播动力学，通过峰值判断传染病在多层网络中的传播行为；文献[11]以SIS传播模型为研究对象，研究双层网络上流行病传播动力学理论；文献[15]描述了一种多层网络构成竞争状态，研究其成功策略。文献[16]研究从物理学角度研究双层网络的上传播行为。然而，当前研究对传播动力学的研究大都以SIS模型为研究对象，并不适用于空间信息网络中信息传播过程。这是因为空间信息网络中节点从S状态接收到信息后变为I状态，并不会再次变为S状态，而更大概率的变为R状态。

为进一步丰富信息传播动力学理论，本文主要以未知状态(Susceptible)-传播状态(Infected)-移除状态(Removed)传播模型(SIR)为研究对象，研究双层均质耦合网络间信息传播动力学，为多层网络间信息传播动力学提供理论参考。首先，构建双层网络间信息传播动力学数学模型，并推导出传播阈值数学公式；进一步分析双层网络传播阈值与单层网络关系，证明双层网络传播阈值相比于单层网络阈值要小；最后通过仿真证明推导理论的正确性以及双层网络的层间连接促进了信息的有效传播。

2 双层网络模型

2.1 网络模型

本节构建的双层网络中信息传播模型存在三种状态：未知状态(Susceptible)，节点当前未知信息；传播状态(Infected)，节点已知信息并会以一定概率传播到与之相连的节点，或以一定概率转变为移除状态；移除状态(Removed)，节点已知信息并不会传播。

假设两个均质网络A网和B网构建成双层网络，A网节点数为M，平均度ka，B网节点数为N，平均度kb。A网和B网度分布符合均匀网络特征[17]。用AB(BA)表示A(B)网到B(A)网的层间耦合网络。双层网络总节点数为M+N，网络间连边为随机连边，如图1所示。

图1中实线为层内连边，表示系统内部实体之间连接关系，虚线为层间随机连边。两个子网中信息传播模型采用SIR模型[18]来描述双层耦合网络上的传播动力学。网络中的节点有边相连表示为邻居关系，信息可以通过节点之间的连边进行传播。未知状态节点(S)会从与其相连的同层已知节点(I)处以概率λa(λb)获得消息，也可以从另一层I状态节点处以概率λba(λab)获得信息，从而演化为I状态。同时，两层网络中I状态个体会以一定概率γa(γb)演化成移除状态(R)，处于移除状态的节点不再向其邻居节点传播信息。

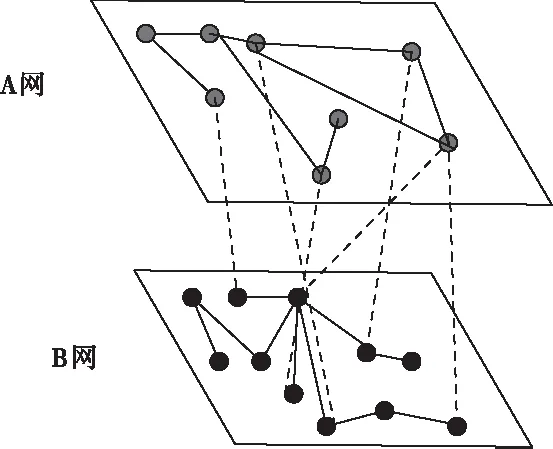
图1 双层网络示意图

2.2 动力学模型

在本文研究中主要考虑双层网络包含两个层间随机耦合的均质网络。子网A(B)节点平均度为ka(kb)，kab(kba)表示A(B)网层间链接平均度。sA(t)(sB(t))表示A(B)中I状态个体在t时刻密度。那么，两个子网信息传播动力学方程可以表示为

(1)

式(1)中第一个式子表示S状态节点减少速率，右边第一项表示S状态节点从层间I状态节点处获取信息，转变为I状态而减少速率，第二项表示S状态节点从B层网络中I状态节点处获取信息而减少的速率；第二个式子表示I状态节点增加速率，分别来自本层和B层S状态节点演化为I状态节点；第三个式子表示移除状态增加速率，μa表示I状态节点演化为R状态节点概率。对于A网，三种状态节点密度加和为1，即

sA(t)+iA(t)+rA(t)=1

(2)

对于B网，同样可得

(3)

根据式(1)和(3)可知，信息在A和B网络中传播，同时也会通过层间连边传播。那么，这种情况下整个网络传播阈值相比于单层网络传播阈值会发生哪些变化，下一节将详细分析。

3 双层网络传播动力学

基于式(1)和式(2)可得

(4)

考虑初始条件，sA(0)=sB(0)≈1，rA(0)=rB(0)≈0，代入式(4)，可得

sA(t)=e(-λa〈ka〉rA(t)-λba〈kba〉rB(t))

(5)

同理，可得

sB(t)=e(-λb〈kb〉rB(t)-λab〈kab〉rA(t))

(6)

结合式(5)和式(2)，可得

(7)

当双层网络信息传播达到稳态时，R状态节点速率不再变化，可得

1-rA(t)-e(-λa〈ka〉rA(t)-λba〈kba〉rB(t))=0

⟹rA(t)=1-e(-λa〈ka〉rA(t)-λba〈kba〉rB(t))

(8)

同理可得

rB(t)=1-e(-λb〈kb〉rB(t)-λab〈kab〉rA(t))

(9)

根据式(8)和式(9)可知，若某种信息可以在双层网络传播，一定是在两层网络都可以传播，因为0≤rA(t)，rB(t)≤1，rA(t)=0，rB(t)≠0不是方程的稳定解，同理，rB(t)=0，rA(t)≠0同样不是稳定解。主要原因如下

以式(9)为例，当rA(t)=0时，式(9)变为

rB(t)=1-e-λb〈kb〉rB(t)

(10)

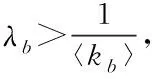
将式(8)写为

(11)

易知λab〈kab〉>0，设置随机参数，分别给出式(11)中y1和y2曲线。从图2中可见，当rB(t)>0时，无论A网有效传播率λa为多少，y1和y2必然会在rA正半轴有一个交点，即rA(t)>0。

另一方面，假设双层网络的传播阈值是λc，当0<λa，λb≤λc时，信息在整个网络中难以传播，当λa，λb>λc时，信息将可以在双层网络中传播。已知，当有效传播率接近传播阈值时，整个网络将会存在很少一部分感染节点，此时λc数值比较小，当单层网络阈值逼近整个网络传播阈值时，式(8)和式(9)可以写为

图2 式(11)中方程曲线比较

(12)

由于λc较小，rA(t)，rB(t)此时数值也较小，对方程左侧进行泰勒级数展开，即ln(1+x)=x+x2/2+O(x)，去除高阶项，可得

(13)

当λa，λb逼近λc时，数值较小，可以等效，λa=λb=λc，进一步可得

(14)

根据式(14)可知，双层网络间的关联矩阵可以表示为

(15)

+1-λabλba〈kab〉〈kba〉=0

(16)

通过求解方程(16)，去掉较大的解，将较小的解作为全局传播阈值[20]，可得

(17)

其中u=4λabλba〈kab〉〈kba〉>0，那么

(18)

显然，根据式(17)可得，

(19)

可见，全局传播阈值小于单层网络间传播阈值，且网络间有效传播率和层间度越大，即u越大，λc也越小，信息更容易在双层网络中传播，即层间链接加速了信息传播。通过合理的设计网络，可以观察到某种信息在A网和B网不能广泛传播，但是可以在双层网络中传播开。

4 仿真分析

图3 传播阈值的理论值(theoretical)与仿真值比较(simulation)

图4给出了双层网络传播阈值与单层网络(A和B)网传播阈值比较，参数与上一个仿真相同。可见，双层网络传播阈值小于单层网络传播阈值，这是由于层间连边增加了信息传播渠道，每个单层网络受到另一层网络影响，增加了信息传播几率，促进信息传播，降低了传播阈值，仿真结果与理论分析结果一致。

图4 双层网络与单层网络传播阈值比较

5 结论

本文以双层均质耦合网络中SIR信息传播模型为研究对象，从传播动力学角度推导了双层均质耦合网络信息传播阈值的数学表达式，分析影响网络信息传播相关因素，并证明了整体网络传播阈值比单层网络传播阈值低。本文研究基于均质耦合网络，是一种理想网络，下一步将以双层异质耦合网络中SIR信息传播模型为研究对象，探索影响双层异质耦合网络信息传播动力学的相关因素。