基于磁偶极子的磁信标标定方法

张明跃，李清华，周子健，李新年

(1.陆军工程大学，石家庄 050000； 2.哈尔滨工业大学，哈尔滨 150000)

0 引言

导航定位技术是社会生活、航空航天、军事武器、工程建设等领域的核心支撑技术。近年来，无人驾驶、水下探测、灾区救援等场景对导航定位技术提出了更高的要求。卫星信号、无线电信号穿透性差，惯性导航误差随时间积累[1-2]，在地下、室内、水中等存在高遮挡的复杂非视距环境中，磁信标导航定位技术因具备信号穿透能力强、误差不随时间积累、位置解算快速等优势，成为解决复杂环境下高精度定位问题的优选方案之一。在磁信标导航定位系统中，精确的磁信标模型是实现高精度导航定位算法的基础。

目前磁信标导航定位信源主要有通电螺线管和永磁体两种结构[3-4],由于永磁体磁场信号不易控制，通常会选择将通电螺线管作为信源，并且通过加入铁芯、优化绕法等方式增大磁场信号强度[5]。文献[6]提出了一种磁梯度张量定位方法，利用磁偶极子模型对环形线圈磁场分布进行了分析；文献[7]对磁偶极子模型进一步优化，提高定位精度；文献[8]提出通过对磁信标产生周期信号做傅里叶变换，进行对目标的相对定位；文献[9-11]提出了一种基于低频交变磁场的磁信标定位技术，通过构建磁场与位置的约束方程，实现对目标位置信息的估计；文献[12]提出基于低频时变磁场特征矢量的磁信标标定方法，提高了目标位置与姿态角解算精度。

目前，磁信标中心的确定方法主要包括以下两种：一种是直接对磁信标的大小进行测量，取几何中心作为磁信标的中心，标定精度受到测量手段与磁信标制作工艺的影响，并且存在通电螺线管几何中心与磁场中心不重合的情况；另一种是利用磁传感器在不同位置测量多组数据，通过每组磁场强度数据可以得到一组距离，进而可以通过求解非线性方程组得到磁信标中心的位置，标定精度受到磁传感器精度与测量数据数量的影响[13]，并且标定过程复杂。针对磁信标磁场中心难以标定的问题，对通电螺线磁场进行建模分析，提出了一种利用通电螺线管磁感应强度分布与位置的关系进行标定的方法，并将磁感应强度信息进行平滑处理，达到提升磁信标在导航定位系统中的解算精度的效果。

1 磁信标磁场模型

磁信标定位系统结构如图1所示。

图1 磁信标定位系统Fig.1 Magnetic beacon positioning system

信号发生器设置信号幅值、频率等参数，通过功率放大器进行电流放大后，传输至通电螺线管中，磁信标发出的磁场特性与设置的信号特性相同。磁通门传感器感受环境中的磁场变化，采集后将信号传输至信号处理装置中，信号处理装置将信号进行滤波后，根据信号的幅值频率等信息解算出位置信息。

低频交变磁场由通电螺线管产生，目标的位置信息由目标所在位置的磁场特征量决定，因此，对通电螺线管磁场分布进行建模与分析是低频交变磁场定位的基础。在实际应用中往往利用磁信标的几何中心近似代替磁信标实际磁场中心，但是由于制作工艺与安装误差等因素的影响，磁信标的几何中心与实际磁场中心并未完全重合，如图1中磁信标所示。

磁信标由具有正交结构的两组螺线管组成，以其几何中心为原点建立的坐标系的X轴、Y轴与以磁场中心为原点建立的坐标系的X′轴、Y′轴之间存在角度误差分别为α和β，根据坐标转换算式

(1)

在已知磁信标几何中心坐标系的坐标情况下，即可求出磁场中心坐标系下的坐标。

为求转换算式，需要先确定磁场中心。通电螺线管磁场模型可以用磁偶极子模型等效,将磁偶极子看作半径为R的圆形载流回路，设环境中磁导率为μ，载流回路中电流大小为I，螺线管的中心为坐标原点O，单磁偶极子模型如图2所示。

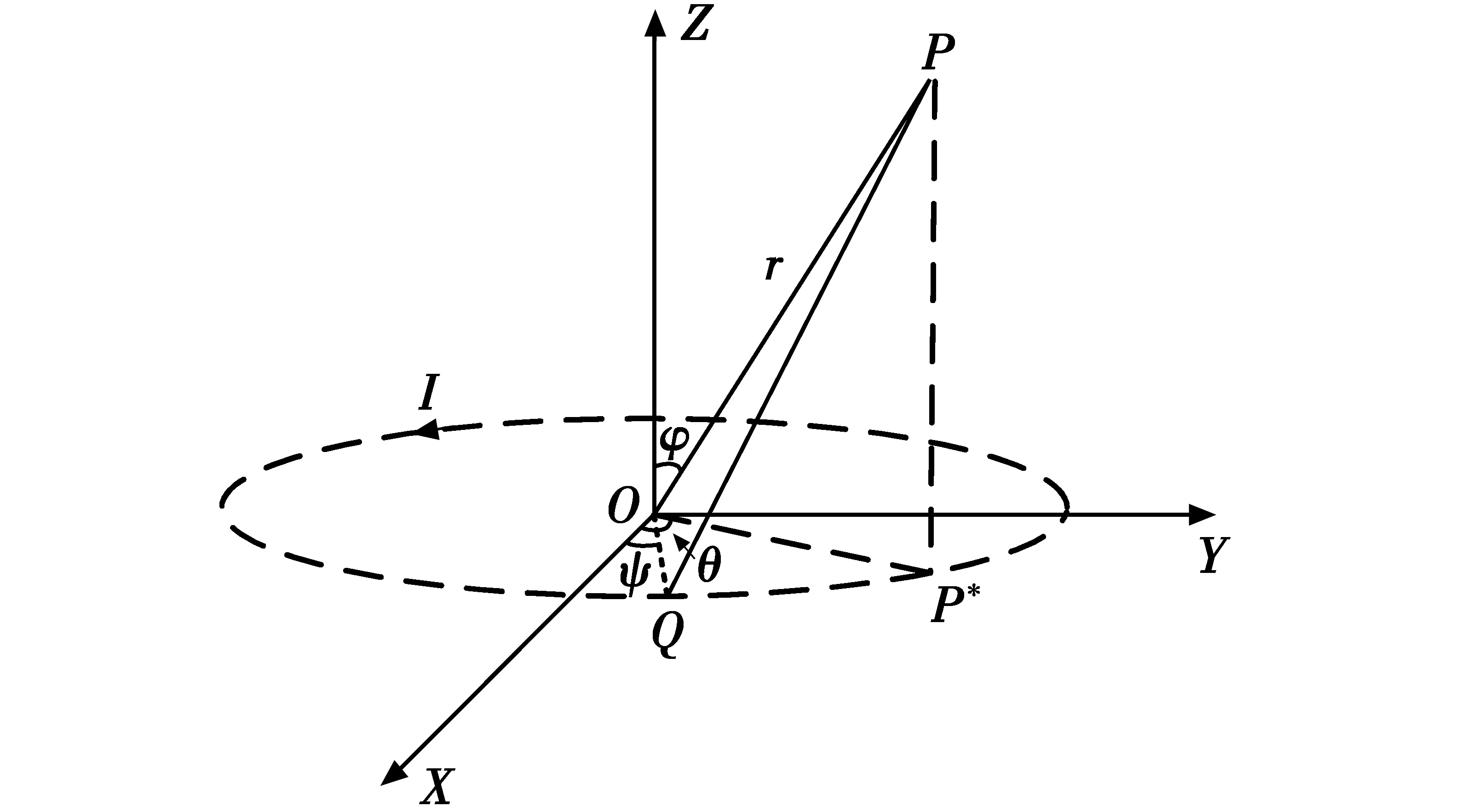
图2 磁偶极子模型Fig.2 Magnetic dipole model

磁偶极子圆形载流回路上任意一点Q(Rcosψ,Rsinψ,0)处取电流微元Idl，其中，ψ为点Q与X轴正方向夹角。根据Biot-Savrt定律，点Q处的电流元在球坐标系任意一点P(r,φ,θ)处(r为点P到坐标原点O的距离，φ为俯仰角，θ为方位角)的磁感应强度为

(2)

(3)

将式(3)代入式(2)得到电流元在点P的磁感应强度为

(4)

对式(4)进行圆周积分，得到单磁偶极子磁感应强度各个分量分布模型为

(5)

工程中测量磁感应强度的仪器是高斯计，其测量方法及其测量原理是将金属或半导体薄片垂直于磁感应强度方向置于磁场中后，根据霍尔效应，当有电流流过时，垂直于电流和磁场的方向上会产生感应电动势。

除了利用高斯计测量磁感应强度，导体切割磁感线产生的感应电动势可以间接反映磁感应强度大小。首先用恒定不变的直流电流信号激励磁信标的一根螺线管，产生恒定磁场，利用磁传感器在螺线管附近按固定方向匀速移动采集数据，或者利用导体在螺线管上方匀速运动，并通过A/D转换采集导体两端产生的感应电动势。

导体切割磁感线时，只有垂直于导体的磁场起作用，只需考虑单个轴向磁感应强度特征，感应电压E为

(6)

式中:S是导体的横截面积；v是导体的移动速度。

切割磁感线方式确定磁场中心的基本原理是电磁感应原理，使用L表示导体相对位置。当导体位于磁场中心时，L为0 mm。由式(6)可知，导体匀速运动时，感应电压与磁感应强度关于导体相对位置的导数成正比。

无论是利用高斯计测量磁感应强度，还是利用移动导体通过感应电压测量磁感应强度，都只能反映垂直于导体或高斯计方向的磁感应强度大小，所以在进行分析时需要计算磁感应强度各个方向的分量与相对位置的关系。

测量不同位置的磁感应强度时，俯仰角表示为φ，线圈中心与磁场中心之间的距离r用相对位置L和线圈垂直高度h表示为

(7)

将式(7)代入式(5)，得出导体相对位置与磁感应强度的关系表达式为

(8)

绘制磁感应强度与相对位置的图像，如图3所示。由图3可以看出，磁感应强度X轴的分量在中心点处为0 T，变化率最大；磁感应强度Z轴的分量在磁场中心处最大，变化率为0。

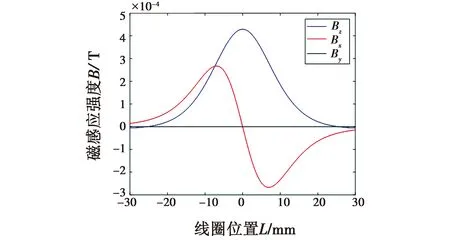
图3 磁感应强度与移动距离关系Fig.3 Relationship between magnetic induction intensity and moving distance

为了验证上述推论，将磁感应强度各个分量对相对位置L进行求导，可以得到

(9)

由式(9)可知，只有当位于磁场中心，即L=0 mm时，磁感应强度X轴分量为0 T，磁感应强度Z轴分量取值最大。另外，根据式(9)绘制出磁感应强度X轴分量的导数图像与磁感应强度Z轴分量的导数图像，可以得出结论，只有在磁场中心时，磁感应强度X轴分量关于相对位置的导数取到唯一最小值，磁感应强度Z轴分量关于导体相对位置的导数为零，在其他位置均不为零。利用这一性质，可以精确确定磁场中心位置。

进行测量时，同时采集通电螺线管磁感应强度X轴方向的分量和Z轴方向的分量，将测量结果取均值以提高精度。

2 仿真与实验

对单个线圈进行有限元仿真，其轴线磁场分量的分布仿真结果与图3计算结果相同。为更直观地研究磁信标中线圈磁场分布情况，对线圈正交方向磁感应强度进行仿真，仿真结果如图4所示。从图中可以看出，磁感应强度X轴分量关于轴线对称，方向相反，Z轴分量在中心处最大。

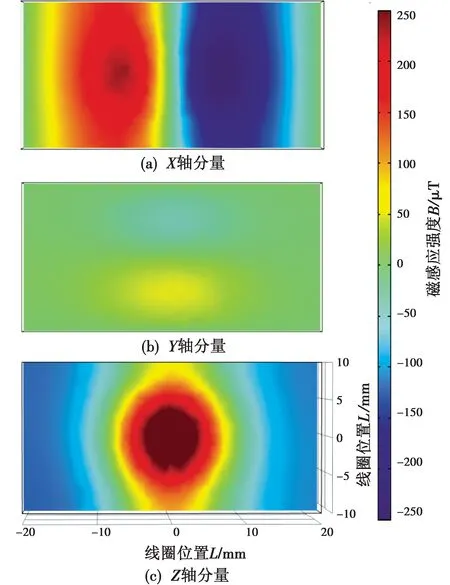
图4 磁感应强度仿真Fig.4 Magnetic induction intensity simulation

对比图4(a)～4(c)有限元仿真结果可以看出，在实际应用时，磁场分量在Y轴分量处有轻微磁场变化，但是与其他分量变化情况相比可以忽略不计。

外部磁场干扰会对磁信标磁场信号测量产生影响，并且由于磁场信号存在自身波动，需要对采集的磁场数据进行平滑处理，减弱自身扰动与外界干扰对磁场数据的影响，再进行求导验证。指数平滑是应用最广泛的一种平滑算法，既保留了移动平均法的优点，又降低了对数据量的硬性要求。由于磁场信号波动具有随机性，平滑系数需要动态调整，使用自适应指数平滑可以减小主观选择平滑系数时的误差。自适应指数平滑程序流程如图5所示。

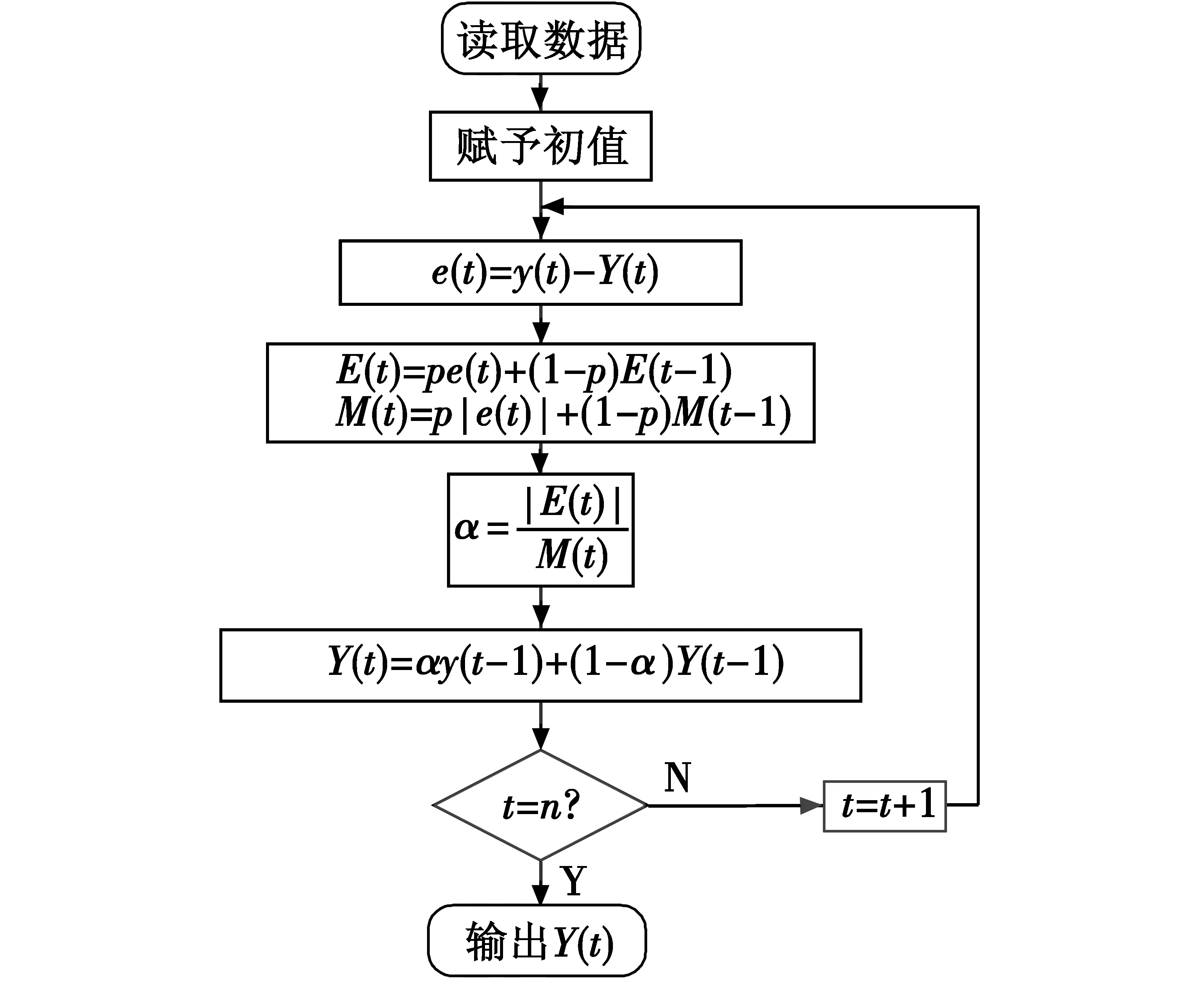
图5 自适应指数平滑程序流程Fig.5 Adaptive exponential smoothing process

图5中,y(t)为t时刻磁感应强度数据测量值，e(t)为t时刻平滑预测误差，Y(t)为t时刻平滑后的磁感应强度预测值，E(t)为t时刻平滑预测误差加权平均，p为加权系数，M(t)为t时刻绝对平滑误差，α为指数平滑系数,n为磁场数据序列数。平滑后的磁感应强度数据及其导数如图6所示。

图6 自适应平滑结果Fig.6 Adaptive smoothing results

从结果可以看出，最后确定的磁场中心误差在0.04 mm，有效减小了磁场中心与几何中心偏差对定位结果的影响。

对标定前后定位精度进行实验对比，实验时每隔3 m进行一次测量，使用磁通门传感器采集不同位置下的磁场，如图7所示。从对比结果可以看出两曲线衰减趋势相同，所以对磁场强度与距离分别进行对数运算。

按照理论推导，磁感应强度分量与距离的关系应该呈现-3次方衰减，将距离与磁感应强度分别取对数运算后，将取对数后的距离与磁感应强度分量进行曲线拟合，如图8所示。从拟合结果可以看出，标定前由于将磁信标几何中心作为起始点，在近距离情况下有较大误差；标定后可以有效提高定位精度。此外，进行标定后，将距离与磁感应强度分别进行对数运算，拟合曲线的系数计算结果为-2.810 7，符合磁场随距离呈-3次方衰减规律。

图7 标定前后磁感应强度曲线Fig.7 Magnetic induction intensity curve before and after calibration

3 结束语

针对磁信标定位中磁场中心与通电螺线管轴线不重合导致的定位误差问题，提出一种基于磁感应强度与位置关系进行标定的方法，推导了通电螺线管横向磁感应强度各个分量表达式，与仿真实验结果相同。利用所提方法将数据进行平滑处理后，使用两个分量进行的磁场中心标定相差0.04 mm，结果表明，使用该方法进行标定能够更精确地确定磁场中心，具有较高的应用价值。