露顶式弧形闸门静动态应力数值分析与试验验证

张 聪，张钰奇，王童童，王 茂，赵华东，李松涛

（1.郑州大学 机械与动力工程学院，河南 郑州 450001； 2.河南省智能制造研究院，河南 郑州 450001； 3.许昌机电职业学院，河南 许昌 461000）

弧形闸门以其优越的水力学特性，被广泛应用于水利工程建设中［1－2］。在实际工作过程中，闸门主要承受来自于水的静载荷及动载荷压力，因此研究闸门在不同水压力下的应力变形情况，对弧形闸门结构保持良好具有重要意义。

Kolkman［3］对某水利枢纽弧形闸门的振动情况进行了研究，应用流固耦合方法分析了水体附加质量情况下该水库闸门的动力响应。Lian 等［4］通过对锦屏水库中孔闸门启闭引起表孔闸门振动现象的研究，得出了接近弧形闸门固有频率的相邻闸门和坝体产生的共振会对弧形闸门的振动产生影响的结论。刘竹丽等［5］基于ANSYS Workbench 平台，对某水利枢纽工程的事故闸门进行了流激振动分析，研究了闭门过程中的水力特性，对闸门及闸室等水工设施的设计、运行及维护提供参考。曹慧颖等［6］对小湾泄洪洞弧形闸门进行有限元建模，分析了弧形闸门在静水压力下各结构的应力变形情况，校核了小湾泄洪洞弧形闸门在静水压力下的结构强度。

目前，对闸门的研究方法主要有原型观测法［7］、模型试验法［8］和数值模拟法［9］。原型观测法需要获取闸门不同运行工况下的实际数据，而闸门的启闭对应一定的泄洪蓄水任务，只能根据有限的启闭条件和水位获得有限的试验数据。基于试验平台的模型试验法要求的水弹性材料难以获得，模型只能在部分物理属性上与原型一致。基于数值模拟法的分析结果在实际应用层面的合理性有待商榷，缺少试验数据的对比使得其正确性难以得到检验。在以往弧形闸门的设计中，取静水载荷乘以动力系数来考虑动水载荷，但简单的动力系数并不能很好地反映闸门在不同工况下运行时的动水载荷情况。

弧形闸门作为重要的水工金属结构被广泛研究，但是自身结构的差异性和工作条件的复杂性使得弧形闸门的分析结果在指导实际工作时不具备普适性，因此针对具体弧形闸门及其特定的工作条件进行分析研究是必要的。本文结合陆浑水库溢洪道弧形闸门的具体结构参数和工作情况，对弧形闸门和门前水体进行建模，原型观测法和数值模拟法相结合，通过流固耦合分析得到闸门受到的动水压力，计算并分析静水压力和动水压力下弧形闸门的应力变形情况，再通过现场传感器获取易于采集的现场数据验证仿真结果的准确性。

1 流固耦合基本理论

闸门与水体的作用是典型的流固耦合作用，水流流动产生动水压力通过水体和门体的耦合作用在闸门门体上。在流固耦合结构分析中，水体遵循质量守恒定律和动量守恒定律，其守恒方程可表示为［10］

式中：t为时间；ff为流体体积力矢量；ρf为流体密度；v为流体速度矢量；τf为剪切力张量；∇为梯度算子。

不考虑能量方程，固体部分守恒可直接由牛顿第二定律导出：

式中：ρs为固体密度；δs为柯西应力张量；fs为固体体积力矢量；为固体域当地加速度矢量。

流体运动边界条件为

式中：x、y、z分别为水体沿水流方向、溢洪道宽度方向、垂直向上方向。

流体和固体耦合体系的有限元方程可以表示为［11］

式中：Aff、Ass分别为流体区、固体区的系统矩阵；Bf、Bs分别为流体区、固体区的外部作用力矩阵；Asf、Afs分别为流体区、固体区耦合矩阵；ΔXf，k、ΔXs，k为水体和结构节点上求解向量的第k个迭代步的改变量。

2 弧形闸门有限元仿真分析

2.1 水库工程概况

某水库设计指标（部分）见表1，其中溢洪道的进口底板高程为313 m［12］。溢洪道设置3 孔弧形闸门，近闸门段溢洪道截面为矩形。

表1 某水库设计指标（部分）

弧形闸门跨度为12 m，闸门的弧面半径为14 m，支铰相对弧形闸门底槛高度为10.5 m，主、次梁跨度均为11 600 mm。闸门结构示意见图1。

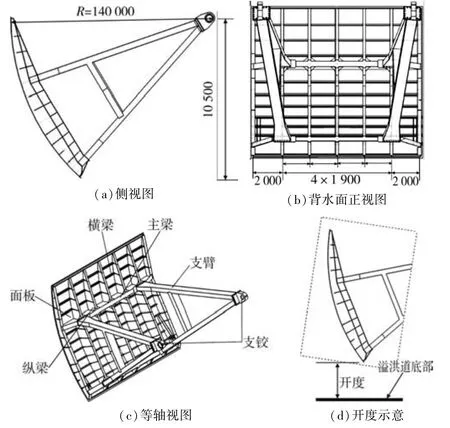
图1 闸门结构示意（单位：mm）

2.2 闸门许容应力及最大挠度

弧形闸门的门体材料为Q345B，弹性模量为206 GPa、泊松比为0.3、材料密度为7850 kg／m3，其材料许容应力［σ］＝225 MPa、［τ］＝135 MPa。参照相关设计规范［13］，在计算弧形闸门等效应力时，可将弧形闸门分为两组考虑。

（1）第一组：闸门面板，其允许应力＝1.43［σ］ ＝321.75 MPa，1.43 为考虑面板进入塑性的系数。

（2）第二组：支臂、主梁腹板、支臂肋板、次梁以及弧形闸门支臂等除弧形面板外的其他部分（在本文以下描述中，统称为其他部分），其允许应力＝0.95［σ］＝213.75 MPa，0.95 为应力折减系数。

通过比较主梁和次梁总变形与挠度之间的关系来校核闸门的刚度，参考相关设计规范［13］，主梁最大挠度与计算跨度之比为1 ∶600，次梁最大挠度与计算跨度之比为1 ∶250。

2.3 有限元模型建立

弧形闸门的面板主要承受水的压力载荷，支臂、翼缘、主横梁腹板、横梁和纵梁翼缘等结构承受面板及支铰传递来的载荷。这些结构的厚度尺寸远小于其他方向的尺寸，属于薄板结构，因此采用壳单元模拟以上结构，定义壳单元厚度为闸门结构的厚度。支铰部分符合实体单元的特征，采用实体单元对支铰部分建模，实体单元尺寸由弧形闸门的实际尺寸确定。水体长度取25 m，其中闸门前水体长度为10 m、闸门后水体长度为15 m。

本文采用ANSYS 仿真分析软件进行有限元分析，最终获得流固耦合有限元模型。离散后的弧形闸门包含32 150 个板壳单元，1 129 个实体单元，66 997 个节点；流体域包含16 320 个实体单元，18 970 个节点。

闸门关闭时，约束闸门两侧的位移，设置闸门竖直方向自由度为0，并在支铰处施加圆柱形支撑约束切向以外的所有自由度，取标准地球重力加速度为9 806.6 mm／s2。闸门开启时，在两吊耳处均施加1 500 kN 拉力，其他约束设置与闸门关闭时一致。

2.4 计算工况

（1）静水工况。静水作用下闸门门前水深为0、1.5、3.0、4.5（汛限水位）、6.5 m（兴利水位）5 种情况，此时闸门均关闭。静水压力可通过静力学分析模块直接设置，通过修改自由表面位置来模拟闸门受到的静水压力。

（2）动水工况。取弧形闸门工作水深为6.5 m（兴利水位），取弧形闸门开度为0（启门瞬间）、1、2、3、4、5、6 m。采用Fluent 软件模拟闸门附近流场，分析兴利水位下闸门的应力及变形随闸门开度的变化情况。流场的入口边界条件设置为速度入口，入口速度为5 m／s；出口设置为压力出口，出口压力为标准大气压力值。使用标准k－ω模型为湍流模型，自由表面的追踪采用VOF 方法实现。通过定义耦合面实现将水体流动产生的动荷载施加到弧形闸门面板上，将动荷载产生的压力导入到弧形闸门结构静力学分析中，以此来模拟动水压力下闸门应力变形情况。

2.5 仿真结果分析

2.5.1 静水工况

静水工况下，对弧形闸门进行静力学分析。6.5 m水深下闸门等效应力云图见图2。在此状况下，闸门面板受到的应力分布较为均匀，且面板受力为上小下大，符合静水压力的分布规律。下支臂的等效应力大于上支臂的，初步分析是因为此状态下支臂主要承受重力，闸门重心位置靠下导致下支臂等效应力较大。

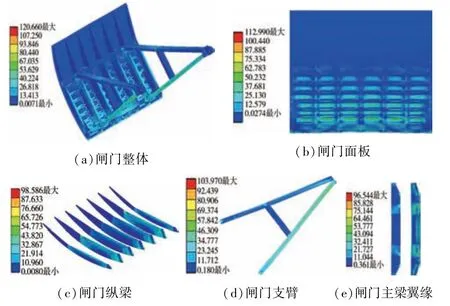
图2 6.5 m 水深下闸门各结构等效应力云图（单位：MPa）

分析闸门变形时主要考虑梁的变形情况，6.5 m水深下闸门总变形云图见图3。从图3 可知闸门纵梁最大总变形发生在中间梁的底部，闸门主梁最大变形发生在下主横梁与闸门支臂连接处，闸门次梁最大总变形发生在底部次梁中间。初步分析，由于闸门在静水压力下关闭时主要受到溢洪道底部的支撑力，因此最大变形部位均在闸门底部。

图3 6.5 m 水深情况下闸门总变形云图（单位：mm）

随着水位上升，闸门面板及其他部位的等效应力和闸门主、次梁的总变形数值变化情况见图4。闸门面板等效应力在0～6.5 m 水深下随着水位上升而增大，其中最大等效应力出现在6.5 m 水深时，为112.99 MPa；最小等效应力出现在0 m 水深时，为107.66 MPa。闸门其他部分的等效应力在0～6.5 m 水深下随着水位上升而增大，其中0 m 水深时等效应力最小，为83.64 MPa；6.5 m水深时等效应力最大，为120.66 MPa。在0～6.5 m 水深下，主梁和次梁的总变形均随水位上升而变大。主梁的最小总变形发生在0 m 水深时，为1.3 mm；最大总变形发生在6.5 m 水深时，为5.82 mm。次梁的最小总变形发生在0 m 水深时，为1.89 mm；最大总变形发生在6.5 m水深时，为7.01 mm。

图4 不同水深的仿真结果

2.5.2 动水工况

对应不同闸门开度，均取闸门门前水位达到稳定值后耦合面上的平均压力值作为闸门开启时的动水压力值。Fluent 流场仿真见图5。

图5 Fluent 流场仿真

兴利水位下，不同闸门开度对应的闸门面板及其他部位的等效应力和闸门主、次梁的总变形情况见图6。闸门在此工作状况下，面板的等效应力值随闸门开启高度的上升而减小，闸门其他部位的等效应力值随闸门开启高度的上升而变大；面板的等效应力由148.71 MPa减小到127.27 MPa，其他部位的等效应力由182.25 MPa 增大至207.63 MPa。初步分析，因为随着闸门开启，闸门面板受水流冲击的面积减小，闸门面板对应的水位降低，所以闸门面板的等效应力随开度增大逐步减小；闸门其他部位的等效应力随着闸门开度增大而变大是因为在闸门开启过程中，重心位置向后移动，应力逐渐集中于支臂等部位。随着闸门开度增大，闸门主梁和次梁的总变形量减小：主梁总变形从8.46 mm减小至4.56 mm，次梁总变形从8.65 mm 减小至4.78 mm。因为在闸门开启过程中面板应力在减小，面板传递给梁结构的荷载也随之减小，所以梁结构的变形随闸门开度增大而减小。

图6 不同闸门开度的仿真结果

2.5.3 结果分析

由以上仿真结果分析得出：闸门面板的最大等效应力为148.71 MPa（在6.5 m 水深下闸门启门瞬间），满足σmax＜321.75 MPa；闸门其他部位的最大等效应力发生在6.5 m 水深下闸门开度为6 m 时，为207.63 MPa，满足σmax＜213.75 MPa。闸门主梁和次梁的最大总变形均发生在6.5 m 水深下闸门启门瞬间，主梁最大总变形满足lmax＝8.46 mm＜10 500／600 ＝17.5 mm，次梁最大总变形满足lmax＝8.65 mm＜11 600／250 ＝46.4 mm。

综上所述，结合参考文献［13］，弧形闸门的等效应力和总变形均在其材料许用范围之内，闸门强度符合其在各工况下正常运行的要求。

3 现场数据验证

3.1 传感器布置方案

传感器在陆浑水库溢洪道闸门的安装布置相对位置见图7。

图7 传感器安装的位置

面板处传感器现场安装布置情况见图8。为保证传感器长期工作稳定，传感器和信号线都经过防水防潮的密封处理，其他部位传感器安装方法与面板处一致。

图8 面板处传感器现场安装布置情况

3.2 静动态应力测试

在实际采集过程中，部分传感器信号丢失，能采集到信息的传感器序号、安装位置、数量及布置形式见表2。

表2 传感器安装位置和数量

试验闸门门前水深为1.4 m，测试弧形闸门静止状态且闸门开度为1 m 时的静态、动态应力变化情况。图9（a）所示为弧形闸门关闭时，在静水压力荷载下的应力测量结果；图9（b）所示为弧形闸门开启至1 m，在动水压力作用下的应力测量结果。

图9 闸门静态、动态应力测量结果

3.3 结果对比

将弧形闸门动态应力测量结果分成两种工况，通过数值仿真分析模拟现场情况，与试验数据进行比较，见图10。

（1）静水工况。对弧形闸门进行静力学仿真，闸门面板受水深为1.4 m 的静水压力荷载。闸门的荷载及约束情况设置与“2 弧形闸门有限元仿真分析”一致。静水工况下仿真值与静动态测量平均值对比见图10（a）。

（2）动水工况。设置闸门开度为1 m，溢洪道进口水深为1.4 m，对弧形闸门进行流场分析与结构静力学单向流固耦合分析，流场设置和弧形闸门荷载及约束情况同“2 弧形闸门有限元仿真分析”。动水工况下仿真值与静动态测量平均值对比见图10（b）。

图10 仿真值与实测值对比

在静水工况和动水工况下，仿真结果和传感器实测应力变化趋势基本一致，且仿真值和传感器实测值的相对误差均在20%以内。因此，仿真结果具有可靠性，弧形闸门各工况的仿真结果能反映实际弧形闸门工作时的应力变形情况。

4 结 论

（1）结合仿真分析和试验验证得出闸门在不同工况下的应力变形情况，表明该弧形闸门符合各工况下安全运行的标准；同时闸门在实际运行过程中，应尽量避免闸门启闭过程中在小开度和大开度状态下的停留。

（2）采用流固耦合数值仿真法计算作用在闸门上的动水压力，最终得到弧形闸门在动水压力作用下的应力变形情况。

（3）结合数值模拟和原型观测两种方法，通过原型观测结果验证了数值仿真结果的准确性，为弧形闸门的结构安全监测技术提供分析依据。