含源项双曲守恒方程的保平衡HLL格式*

彭国良，王仲琦，张俊杰，任泽平，谢海燕，杜太焦

（1.北京理工大学 机电学院，北京 100081；2.西北核技术研究所，西安 710024）

引言

含源项的双曲守恒方程在很多领域都有应用，如气体动力学[1]、浅水波[2]、天文模拟[3]、血液流动[4]等.源项的存在会改变方程解的性质，当方程趋于稳态时，通量梯度与源项应处于完全平衡的状态，但由于网格离散误差，传统的计算格式不能保证平衡状态，导致解在平衡态附近有虚假的振荡.许多物理问题实际上是稳态解的小扰动，如果计算格式设计不好，离散误差可能淹没实际的扰动解.尤其计算网格较为粗糙时，这种误差更大.使用非常细的网格可以减少离散误差，但对大尺度问题细网格的计算成本过高.因此，设计保平衡格式对解决大尺度流动模拟具有重要意义.

为减少平衡态附近的离散误差，学者们发展了很多保平衡格式.Cui[5]和Ozcan[6]通过将动量方程的源项空间积分后合并到压力项，发展了保平衡中心迎风格式(WB-CU).计算中发现这种方法存在的问题是压力不能保正，对高空大气等低密度、低压力问题容易出现负压力.文献[7]介绍了通过引进新的变量将含源项的非守恒方程变为守恒方程的形式，源项与压力等变量的离散保持一致，从而保证平衡.这种方法求解的是原问题的松弛方程，对大尺度高空大气扰动问题，其计算精度较差.Chalons 等[1,7]和Franck 等[8]利用基于Lagrange 投影的方法，求解Lagrange 坐标形式下含源项的近似Riemann 问题，针对Euler 方程发展了新的保平衡格式.这类方法精度较高，但向波系更复杂的磁流体等问题推广时计算较复杂，对已有成熟程序的改动也比较大.本文基于常见的HLL 有限体积方法[9-11]，发展了一种新的保平衡格式，期望尽可能简单地实现含源项双曲守恒方程保平衡的求解.

1 含源项的HLL 近似Riemann 求解器

含源项的双曲守恒方程为

式中，U为待求解变量，F为矢通量，Q为源项.

如图1所示，方程（1）的HLL 近似Riemann 解为

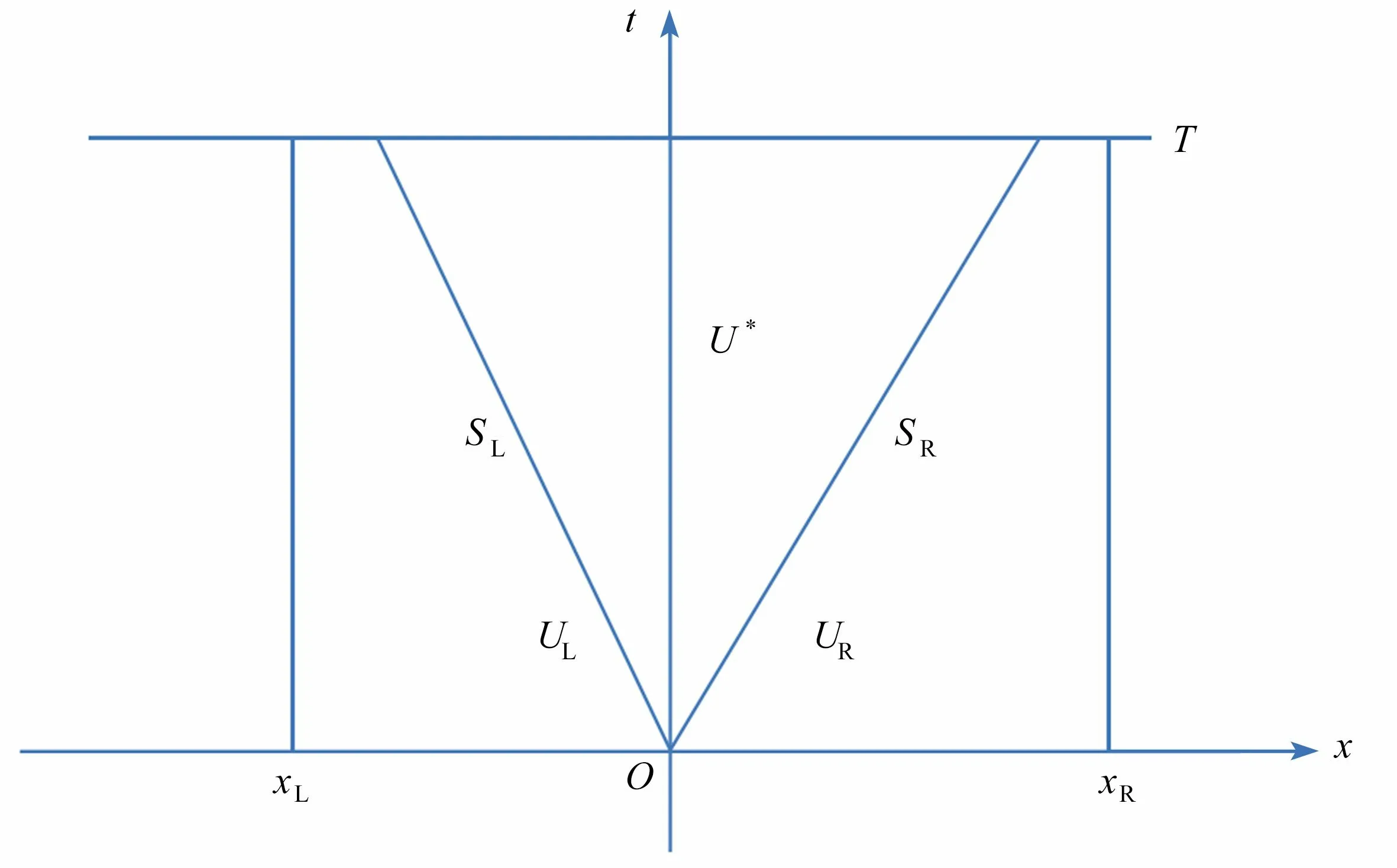
图1 HLL 近似Riemann 解示意图Fig.1 The sketch of HLL approximate Riemann solvers

式中，SL表示左行波的最大波速，SR代表右行波的最大波速.

在控制体[xL,xR]×[0,T]内，式(1)可写成积分形式[12]：

式中，∆x=xR−xL.另外，等式左边可写成

比较两式右边可得

通量项F的表达式为

将式(5)代入可得

源项的平均值可近似写成

从而得到计算格式为

含Van-Leer 限制器的二阶守恒重构格式为[13]

时间积分可用2 阶Runge-Kutta 方法，即

2 保平衡HLL格式

对含重力源项的一维流体Euler 方程，方程（1）中的各项可写成

波速为

式中，a为声速.最大波速为

对含重力源项的一维理想磁流体方程，有

波速为

式中，a，c分别为声速、磁声波速.最大波速为

平衡态时u为0，与u相关的对流输运通量也要为0，故需对通量计算公式(7)进行修正.利用文献[5]使用的技巧，以磁流体方程的通量式(15)为例，速度u为0 时，对流通量的第1，3，4，5 分量也应为0.故式(7)可以写成

式中，上标（i）表示第i个分量，H(u)为与速度相关的修正项，需满足

可取

式中，C和m是与精度有关的计算参数，本文中C取1000，m取6.

传统的HLL 格式的通量项为[9]

对比式(18)和式(21)可知，新格式与传统格式相比，仅需很小的改动.

下面以理想磁流体方程为例证明本文提出的修正HLL 格式满足保平衡的要求，即格式在平衡态时能恢复为静力平衡方程.Euler 方程的情形的证明也可同理得到.

平衡态时，满足条件uL=uR=0.由式 (15)可得

代入式(18)可得

化简为

即稳态情况下计算的方程变为∂xp=ρg，满足静力平衡条件.故本文提出的格式是保平衡格式.

3 数值算例

等温大气的扰动算例是用来测试保平衡格式的常用算例[5,6,8]，但一般文献中设置的计算尺度较小.本文测试在大尺度条件下各种格式的效果.

3.1 大尺度大气流体的扰动

设大气的初始条件为

g=9.8 m/s2,c=300 m/s,l=80 km,xc=50 km,η=1 Pa

式中，.设大气为理想气体，比热比取1.67，计算域为[10,90]km，边界条件采用文献[14]给出的静态等温边界：

时间积分采用2 阶Runge-Kutta 积分，重构方法采用含Van-Leer 限制器的二阶守恒重构格式.网格数取两组：N=20 和N=100，分别用传统的HLL 格式、本文提出的WB-HLL 格式、松弛格式（relax）、Lagrange 投影格式（LA）和WB-CU 格式计算，计算时长100 s.另外，用WB-HLL 格式计算了N=1000 的情形作为参考的精确解.由于计算中WB-CU 格式出现负压力无法完成计算，下面只比较其他4 种格式.

图2 给出了不同格式和网格计算的扰动速度.由于松弛格式计算结果与其他格式相差较大，为了便于比较，在图2(b)中没有展示松弛格式计算的结果.从图中可以看出，相同网格精度下，WB-HLL 格式与Lagrange 投影格式精度相当，比传统的HLL 格式计算精度更高；网格加密时，WB-HLL 格式也比传统的HLL 格式收敛更快.

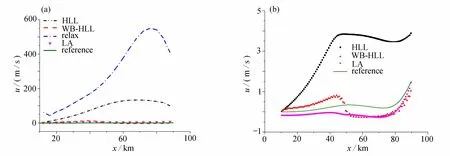
图2 不同格式计算的流体扰动速度：(a)网格数N=20；(b)网格数N=100Fig.2 Fluid perturbed velocities with different schemes:(a)grid number N=20;(b)grid number N=100

3.2 大尺度大气磁流体的扰动

为验证WB-HLL 格式在磁流体问题中的计算效果，我们将3.1 小节的算例改成磁流体算例.由于Lagrange 投影格式推广到磁流体问题时较为复杂，本算例仅比较WB-HLL 格式和HLL 格式.初始条件为

图3 给出了磁流体方程不同格式和网格计算的扰动速度，图4 给出了不同格式和网格计算的磁场结果.从图中可以看出，对磁流体方程，与传统的HLL 格式相比，WB-HLL 格式计算精度更高，收敛更快.

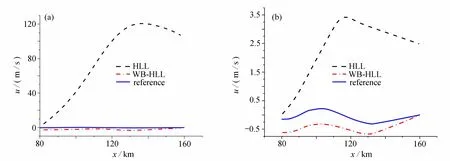
图3 不同格式计算的磁流体扰动速度：(a)网格数N=20；(b)网格数N=100Fig.3 MHD perturbed velocities with different schemes:(a)grid number N=20;(b)grid number N=100

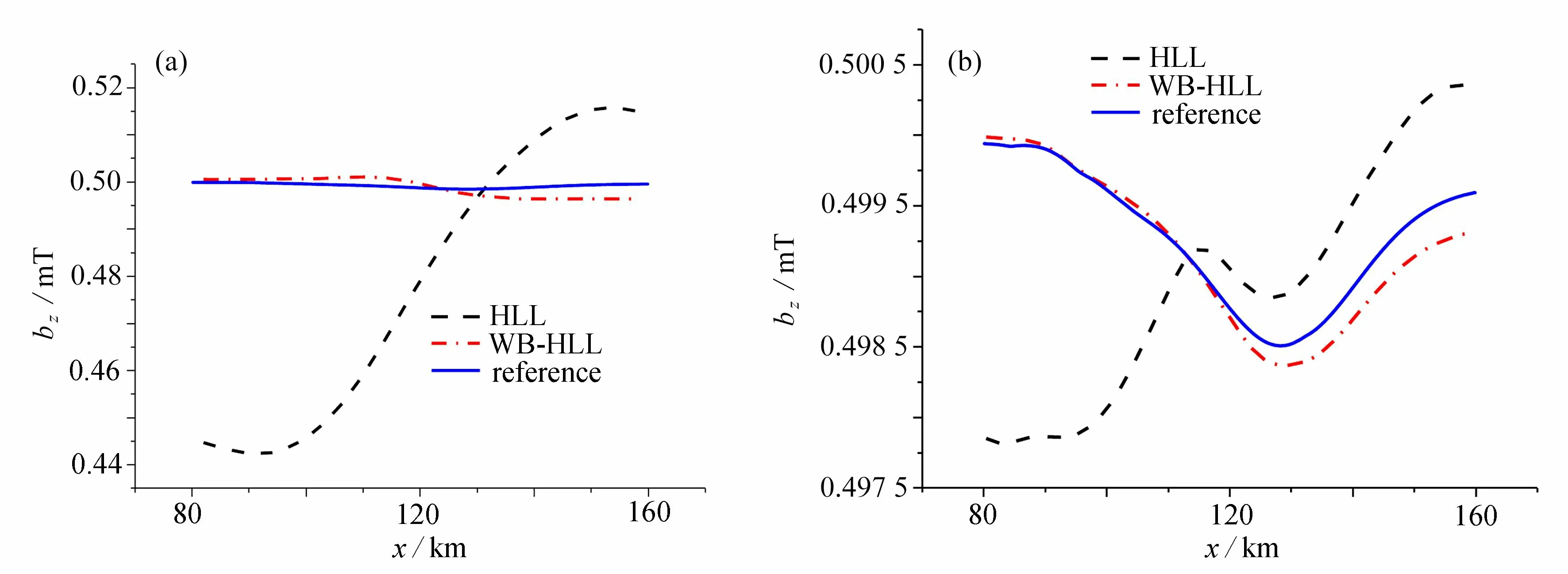
图4 不同格式计算的磁流体磁场：(a)网格数N=20；(b)网格数N=100Fig.4 MHD magnetic results with different schemes:(a)grid number N=20;(b)grid number N=100

4 结论

本文构造了含源项的HLL 型近似Riemann 求解器，对通量计算格式进行修正，提出了保平衡的HLL 有限体积计算格式，并给出了保平衡证明.与经典HLL 格式相比，本文的计算格式只需很小的改动.数值算例表明，针对大尺度含重力源项的Euler 方程，在精度与收敛速度方面，本文的新格式与Lagrange 投影方法相当，与传统HLL 格式相比有较大提高.针对大尺度含重力源项的理想磁流体方程，新格式在精度与收敛速度方面与传统HLL 格式相比也有较大提高.