计及微网发电与电力交易数据的柔性优化控制算法建模与仿真

黄靖茵，胡鑫，黄康乾，周睿，黄志生

（广东电力交易中心有限责任公司，广东广州 510600）

近年来，随着分布式发电(Distributed Generators，DG)的不断发展，光伏、风电等装机容量逐年上升，微网在本地完成电力交易也成为了必然趋势[1]。由于DG 输出存在随机性、波动性和间歇性，传统电力交易市场机制已无法满足微网电力市场交易需求[2-3]。与原有电力市场单一的销售模式不同，微网的发展使用户有了更多的购电选择。因此如何灵活地完成电力交易，并实现微网电能的优化控制成为了当前的研究热点[4-5]。

针对上述问题，该文构建了一种柔性优化控制算法模型，采用柔性电价来构建目标函数，并通过改进鲸鱼优化算法(Whale Optimization Algorithm，WOA)进行求解，得到了最佳的电力交易方案与系统运行方式。

1 微网电力交易的建模

1.1 微网电力交易

在低碳环保政策的推动下，光伏、风力等清洁能源开始广泛用于发电，且在电网中的渗透率越来越高，从而促进了微网电力交易的发展[6-7]。微网电力市场交易模式如图1 所示。

图1 微网电力市场交易模式

不同于传统电力交易，微网电力交易市场主要集中于用户侧，其交易量相对较小且较为灵活。同时，用户与发电厂商能够在本地市场进行电力交易，且交易双方处于平等地位。而电能传输等物理层面由交易平台保障执行，即电网公司负责运营和监管平台[8]。

1.2 柔性电价

由于微网中的分布式能源发电存在不确定性，且需要考虑该不确定因素对系统的影响[9]。因此引入经济性目标，并提出柔性电价，通过调节微网的交易电价，实现系统的稳定、经济运行。柔性电价的计算方式为：

1）当发电量小于用电量时：

2）当发电量大于用电量时：

式中，ψ′为柔性系数；Bi为各电厂投资成本下的日发电量；λ为发电成本因子；Cα为年投资成本；Cβ为年维护成本。

由于柔性电价会随着发电量而改变，因此可能会出现极端波动情况，故需要根据微网的最大和最小资源量水平以及标准电价来设置电价的上下限[10-11]。

2 电力交易的柔性优化控制算法

根据微网运行成本最小化的优化目标，利用改进WOA 算法进行求解，以得到最佳的电力交易方案，进而实现系统的柔性优化控制。

2.1 改进鲸鱼优化算法

WOA 是一种新兴的基于鲸鱼捕猎行为的优化算法，其可使用特殊的方法成功捕获猎物[12]。WOA的处理流程如图2 所示，其包括搜寻猎物、包围猎物、泡网攻击三个阶段。

图2 WOA的处理流程

1）搜寻猎物：若p＜0.5 且，则进入随机搜索猎物阶段，且搜索代理在空间中随机游荡以搜寻猎物。该数学模型与位置变换公式如下：

2）包围猎物：若p＜0.5 且 ||A→≤1，则进入包围猎物阶段，并确定猎物所在位置并包围猎物。此时搜索代理将更靠近最佳位置，且该位置更新计算如下式所示：

3）泡网攻击：若p≥0.5，则进入螺旋收缩包围和泡沫网攻击阶段。计算搜索代理与最优搜索代理间的距离，进而构建螺旋数学模型，以更新代理位置。该阶段计算公式如下：

WOA 的全局搜索能力较弱，且易陷入早熟收敛。为解决这一问题，引入长步长的柯西变异以及短步长高斯变异，以增强WOA 的局部搜索能力，从而提高收敛精度[13]。柯西变异具有变异范围广的优势，但通过柯西变异进行随机搜索容易跳出局部极值[14-15]。因此，对WOA 随机捕食阶段的位置更新修改如下：

式中，r3是介于[0,3]之间的随机数。

高斯变异是一种改进关键搜索区域局部搜索能力的变异操作方法[16]。其在突变过程中，使用随机数替换原始基因值，即对全局最优搜索代理进行变异，以加强WOA 的局部搜索能力。则全局最佳搜索代理更新如下：

式中，n∈N(0,1)；为通过高斯变异得到的全局最优搜索代理；r4为介于[0,1]之间的随机数；k为局部变异概率。

2.2 微网柔性优化控制策略

假设微网中存在G个发电厂商，且集合为g={1,2,…,G}，则其可能的电力交易策略表示为：

式中，Eu为用户侧所需的电量；Eg为第g个发电方售出的电量。

通过优化交易策略以及调节柔性电价实现系统运行成本的最小化，其优化控制流程如图3 所示。

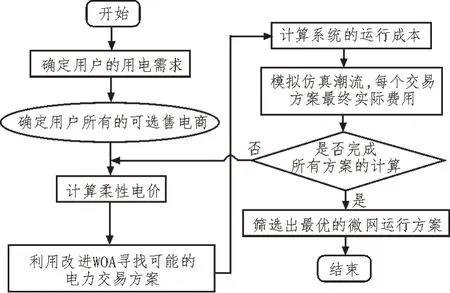
图3 电力交易柔性优化控制流程

在电力交易中，首先确定用户的负荷需求以及微网中的发电量，确定用户可选的售电商，并依据双方电量的实际情况计算柔性电价；然后根据柔性电价，发电方和用户均会进行相应的调整，例如用户增加或减少自身用电量，发电厂将电量存储或售出；最终通过改进WOA 算法寻找电力交易方案，并模拟每种交易策略的成本，筛选出最优的微网运行方案。

3 实验结果与分析

基于Matlab 搭建实验仿真平台，其中包括三个光伏电厂、两个风电厂、一台柴油发电机组以及储能站。由于光伏(PV)和风力(WT)发电量几乎不可控，因此其电量调节仅能通过外加电量或存储电量，PV和WT 的功率输出情况如图4 所示。

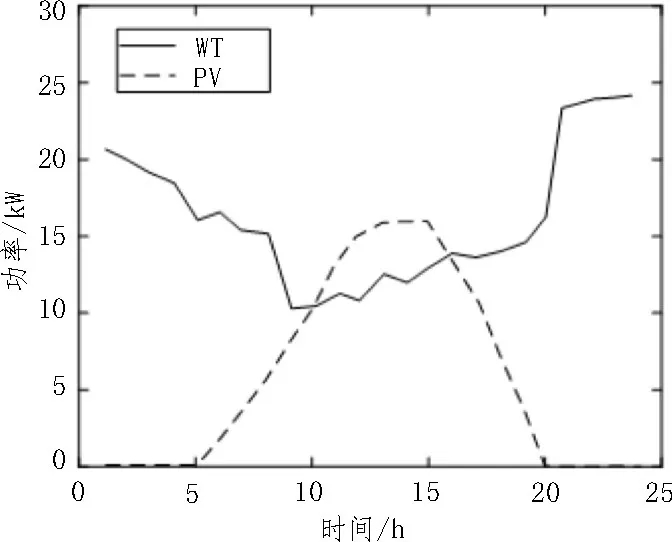
图4 PV和WT的功率输出

3.1 柔性电价结果分析

柔性电价随着用电量和发电量的变化而实时变化。通过控制柔性电价能够优化分布式能源的功率输出，并减少系统运行费用。选取时段6:00-18:00内微网电量与柔性电价的关系，如表1 所示。

表1 微网电量与柔性电价

从表1 中可以看出，柔性电价随着用电量和实际发电量的改变而改变。当实际发电量无法满足用电需求时，即分布式能源发电无法满足微网用电需求，则上调柔性电价；反之，当微网电量过剩时，则下调柔性电价并减少电力输出。在14:00-16:00 时间段内，光伏发电量较大，而用户需求较低，故降低电价至0.437 元。这样不仅可以鼓励用户多用电，且能控制储能装置进行储能并减少柴油发电机的出力，从而实现微网运行的最大经济化。

3.2 优化结果对比

基于微网实时电力交易数据，并利用所提柔性优化控制算法进行处理，最终得到除光伏、风力以外分布式电源的最佳功率输出，如图5 所示。

图5 其他分布式电源的最佳功率输出

从图5 中可以看出，当分布式能源发电大于负荷时，可将剩余电量储存在储能装置中，如14 h 左右，储能出现明显的上升趋势，而燃料电池(FC)减少发电量以控制成本；当分布式能源发电小于负荷时，储能装置放电，当储能未有剩余电量后，燃料电池(FC)和柴油发电机(DE)开始产生大量电能，如19 h 左右。由此可以看出，该控制算法保证了FC、DE 发电单元输出的平稳并尽可能地降低输出。由于二者具有相对较高的燃料成本与污染排放，所以不平稳的输出也会降低其运行效率。

为了论证所提算法的性能，将其与文献[3]、文献[5]进行对比。该微网总运行成本优化对比如图6所示。

图6 微网总运行成本优化对比

从图6 中可以看出，相较于其他算法，所提算法的运行成本最低，且最高点在晚间，平均值未超过3 万元。由于晚间用电量大且光伏等分布式能源出力不足，因此柔性电价高，其他燃油机组发电成本也相对较高。文献[3]采用群体主动学习算法，由于其寻优能力不足，所以整体运行成本较高，总体上平均值已超过4 万元。文献[5]主要考虑碳排放进行电力交易优化控制，其优先消耗分布式能源，所以导致整体经济性一般。而所提算法综合各方面成本因素并结合柔性电价，且利用改进WOA 进行了优化，从而得到最为经济的系统运行方式。

4 结束语

新能源发电的快速发展推动了电力市场的改革，而微网内电能交易的优化控制缺乏一定的经济性。为此，在充分考虑微网发电与电力交易数据的情况下，该文构建了一种柔性优化控制模型。基于Matlab仿真平台对该文算法进行实验论证的结果表明，柔性电价能够较好地呈现用电量与发电量之间的关系，并作用于系统，控制DG 功率最优输出，且在提高系统经济性的同时又优化了微网的能源结构。但该文仅考虑了单个微网，其优化控制性能存在一定的局限性。因此在接下来的研究中，将考虑微网互联以便提高微网能源的稳定性及系统的经济性。