锚拉桩-锚索框架梁组合结构加固边坡可视化模型试验

2023-03-10陈建峰杜长城石振明

同济大学学报（自然科学版） 2023年2期

陈建峰，杜长城，祁昊，彭铭，石振明

（1.同济大学土木工程学院，上海 200092；2.中国（广东）自由贸易区前海蛇口片区管理委员会，广东深圳 518052）

锚拉桩是在抗滑桩上安装预应力锚索，以减小抗滑桩桩身弯矩和剪力，并减小滑坡体位移量和较快稳定滑坡体的一种支挡结构。锚拉桩与锚索框架梁形成的组合结构既可依靠锚拉桩限制坡体深层变形，又可利用预应力锚索限制坡表变形、减小锚拉桩设计荷载，因此可同时保证边坡整体和局部稳定［1-2］。

目前对抗滑桩-锚索框架梁组合结构加固边坡已开展了一些研究。Yuan等［3］对抗滑桩和锚索框架梁组合结构加固边坡进行数值模拟，发现组合结构可使边坡的滑移模式发生改变。Li等［4］对抗滑桩和锚索框架梁组合结构加固边坡进行现场测试，发现锚索和抗滑桩协同受力，其荷载分担比分别为33.9 %和66.1 %。赵晓彦等［5］对抗滑桩和锚索框架梁组合结构加固边坡的设计方法进行优化，实现了锚索预应力和抗滑桩被动力的协调作用。付晓等［6-7］研究地震作用下抗滑桩和锚索框架梁组合结构加固边坡的动力响应特性，结果表明锚索与抗滑桩协同受力，且地震作用强弱对桩和锚的荷载分担比有较大影响。陈建峰等［8］采用三维有限元模拟抗滑桩-锚索框架梁组合结构加固边坡方案的稳定性，分析不同强度折减系数下抗滑桩和锚索的受力特性以及抗滑桩和锚索的荷载分担规律。

目前还未有对锚拉桩-锚索框架梁组合结构加固边坡开展研究的报道。本文采用一种光学镀膜用玻璃砂（高纯度熔融石英砂）和2种矿物油制备成的透明土［8-11］，开展锚拉桩-锚索框架梁组合结构加固边坡的可视化模型试验及无加固边坡的对比试验，并结合粒子图像测速技术，展现边坡内部位移场演化及其滑移破坏过程，以探讨锚拉桩和锚索框架梁在加固边坡过程中的协同作用机制，为相关支挡工程的设计提供参考。

1 模型试验概况

1.1 模型尺寸及试验装置

锚拉桩-锚索框架梁组合结构加固边坡模型试验模拟的原型边坡高度6 m、坡度37°、基岩倾角50°。距离坡脚4 m 处的坡中布置有截面尺寸为0.8 m×0.8 m的方形抗滑桩。桩长4 m，桩间距3.2 m，抗弯刚度EI=1.02×109N·m2。坡面沿x方向布设有2排锚索框架，每排3 根。相邻锚索沿x方向间距为1.4 m，沿y方向间距为1.6 m。锚索外径40 mm，孔径110 mm，锚固段长2 m，自由段长8～ 9 m。试验取模型率N=40。图1为缩尺后的模型示意图。

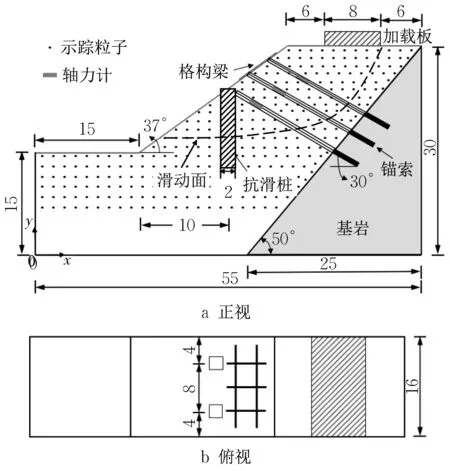
图1 模型示意（单位：cm）Fig.1 Schematic view of modeling (unit: cm)

模型试验装置主要包括模型箱、加载系统、数码相机和数据采集系统，如图2 所示。根据模型率制作模型箱，其内部长、宽、高分别为55 cm、16 cm、35 cm。箱侧壁为19 mm厚钢化玻璃，四周用角钢固定，相邻箱壁的连接处用玻璃胶密封。坡顶设置有刚性条形加载板，截面长、宽分别为15.6 cm×8 cm。可通过调节加载板与水平面之间的倾角以产生不同深度的滑动面。试验加载板倾角固定为10°。加载装置如图3所示。

图2 试验装置布置Fig.2 Site layout of experimental apparatus

图3 加载装置Fig.3 Loading device

加载系统为WDW-600KN 伺服控制电子万能试验机，采用位移控制方式加载。观测剖面（即抗滑桩和锚索中心线连线形成的纵剖面，距离箱壁4 cm）上均匀布置有示踪粒子（图1），用以结合粒子图像测速技术分析边坡土体位移场。试验中使用分辨率为2 592×1 728的佳能550D数码相机拍摄照片。

试验的同时开展了无加固边坡的对比试验，以确定其滑动面及其稳定性，为锚拉桩-锚索框架梁组合结构加固边坡模型试验提供合理的锚拉桩长度。

1.2 试验材料

模型边坡材料为均质透明砂土，其由光学镀膜用玻璃砂与孔隙液体配制而成。玻璃砂SiO2质量分数为99.99 %，折射率为1.458 5，颗粒比重为2.24，平均粒径D50=1.42 mm，不均匀系数Cu=2.08，曲率系数Cc=1.16。孔隙液体为3#白油和15#白油按体积比为5：1 混合配置的折射率为1.458 3 的无色、透明液体。此液体折射率与玻璃砂折射率基本一致，因此透明砂土的透明厚度可达14 cm。试验按相对密实度Dr=85 %建造均匀的透明土边坡，其初始孔隙比为0.628。通过直剪试验得到该密实度下透明土的黏聚力c=0，内摩擦角φ=45°。通过室内一维压缩试验可得在100～ 200 kPa 荷载范围内透明土压缩模量Es=18.1 MPa，压缩指数Cc=0.04，属于低压缩性土。

基岩采用水泥砂浆进行制作，其配比为水、水泥、砂的质量比为1：2：4。养护1 周后，其黏聚力c=3.54 MPa，内摩擦角为φ=46°。

支挡结构包括抗滑桩、锚索和框架梁。模型桩为铝合金制方形管桩，其截面边长D=2 cm，壁厚t=0.5 mm。锚索采用直径1 mm的钢绞线模拟，锚固段长5 cm，自由段长由原型缩尺后得到。锚固段的制作方式参照文献［7］，以模拟锚索的拔出失效，如图4 a所示。采用WDW-600 kN 伺服控制电子万能试验机对锚索的极限拉拔荷载进行了标定，其极限拉拔力约为15.8 N。模型框架梁采用铝合金制成，如图4 b所示，其长、宽、厚分别为14 cm、6.5 cm、0.7 cm。

图4 锚索框架梁照片Fig.4 Photo of anchor cable frame beam

1.3 试验步骤

（1）按照指定水灰比和试验方案制作基岩，并按规范养护1周，而后将基岩放入模型箱中，其周边用硅橡胶涂抹密封。

（2）将15#白油和3#白油按比例配制透明土孔隙液体并缓缓加入模型箱，而后将玻璃砂分层填入，按相对密实度85 %分层振密至地基高度15 cm，同时将抗滑桩底端埋入指定位置。将示踪粒子均匀布置于支挡结构两侧，形成观测剖面。

（3）将边坡成型装置放入模型箱内并与箱体固定，继续填入玻璃砂，按相对密实度85 %分层振密至边坡高度15 cm，同步布置示踪粒子。

（4）拆除边坡成型装置，通过穿孔螺栓将锚索和抗滑桩桩头、框架梁节点连接起来。通过向外旋转螺杆实现锚索预应力施加，观察并记录预应力动态变化情况直到预应力值稳定为止。

（5）布置数码相机并调整至合适位置，以得到清晰完整的边坡剖面图像，并设定连续2 张照片的拍摄时间间隔为10 s。

（6）固定条形荷载并将其调整至指定位置，而后启动万能试验机按2 mm·min-1的速率进行加载，同时进行数据和图像采集。采用基于MATLAB 的Geo-PIV 粒子图像测速分析程序对图像进行分析，以获得边坡位移矢量图。

2 试验结果与分析

2.1 无加固边坡的变形破坏特征

图5为无加固边坡坡顶（即加载区）荷载-位移曲线。由图可见，坡顶荷载随竖向位移先逐渐增大至峰值应力48 kPa，而后逐渐减小。

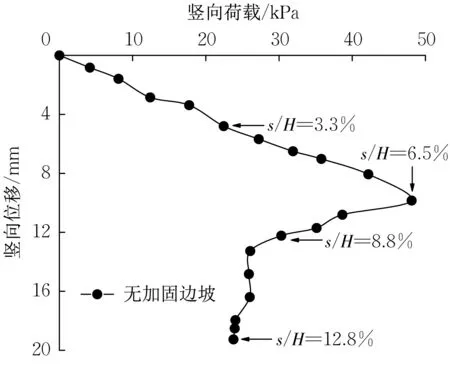
图5 无加固边坡的荷载-位移曲线Fig.5 Load-displacement curve of unreinforced slope

图5 曲线上标注了竖向位移s与坡高H的比值s/H分别为3.3 %、6.5 %、8.8 %和12.8 %所对应的点。图6 则为这些点对应的边坡位移矢量图，图中横坐标和纵坐标均通过除以抗滑桩截面边长D进行归一化处理。由图6可见，当s/H=3.3 %时，边坡变形较小，且主要集中在坡顶，边坡土体被压密；在荷载达到峰值时（s/H=6.5 %），土体位移向下和向坡面方向发展，坡体位移明显增大；随着继续加载至s/H=8.8 %时，土体变形范围扩大并持续向坡面方向发展；继续加载至s/H=12.8 %时，土体位移进一步增大，且根据图中位移矢量的方向和大小可判断边坡内滑动土体与周围土体存在明显的分界面，此分界面即为边坡滑动面（图6 d）。

图7 为加载至s/H=12.8 %时边坡的变形图，坡体内形成了一条近似圆弧形状的滑动面，与图6 d位移矢量图揭示的滑动面一致。

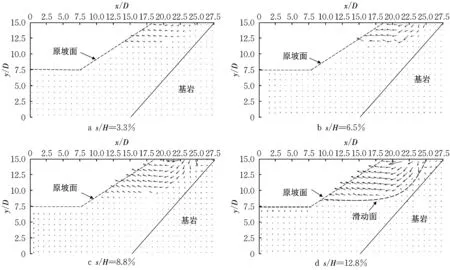
图6 无加固边坡的位移矢量Fig.6 Displacement vector of unreinforced slope

图7 加载末期无加固边坡的变形Fig.7 Deformation of unreinforced slope at the end of loading

2.2 锚拉桩-锚索框架梁组合结构加固边坡的变形破坏特征

模型试验中的锚拉桩嵌固长度是根据图7 所得出的无加固边坡滑动面深度确定的。依据滑坡防治设计规范［12］，初步选定锚拉桩嵌固长度时，桩嵌固长度可取桩长的1/4～ 1/3，而本文桩侧壁土体性质一般，其最终长度取为桩长的2/5。图8 为锚拉桩-锚索框架梁组合结构加固边坡所对应的坡顶荷载-位移曲线。由图可见，组合结构加固边坡的坡顶极限承载力为168 kPa，其值较无加固边坡提升了约250 %，这说明锚拉桩和坡面锚索框架组合结构可显著提升边坡的承载能力和稳定性。

图8 曲线上标注了s/H分别为 3.3 %、7.2 %、11.3 %和17.6 %所对应的点。图9 为各标注点对应的边坡位移矢量图。由图可见，加载初期s/H=3.3 %，边坡变形较小，仅桩顶及加载板附近土体产生微小位移；继续加载至s/H=7.2 %时，土体有向下和向坡面方向的发展趋势，但土体位移总体不大；加载至峰值荷载s/H=11.3 %时，土体变形范围明显加大加深，同时上部第1、第2 排锚索相继变形失效，锚拉桩发生轻微倾斜；最终加载至s/H=17.6 %时，土体位移进一步增大，锚拉桩发生明显倾斜，桩身锚索也发生失效，并于土体内部发展出切过桩端和坡脚的滑动面（图10）。

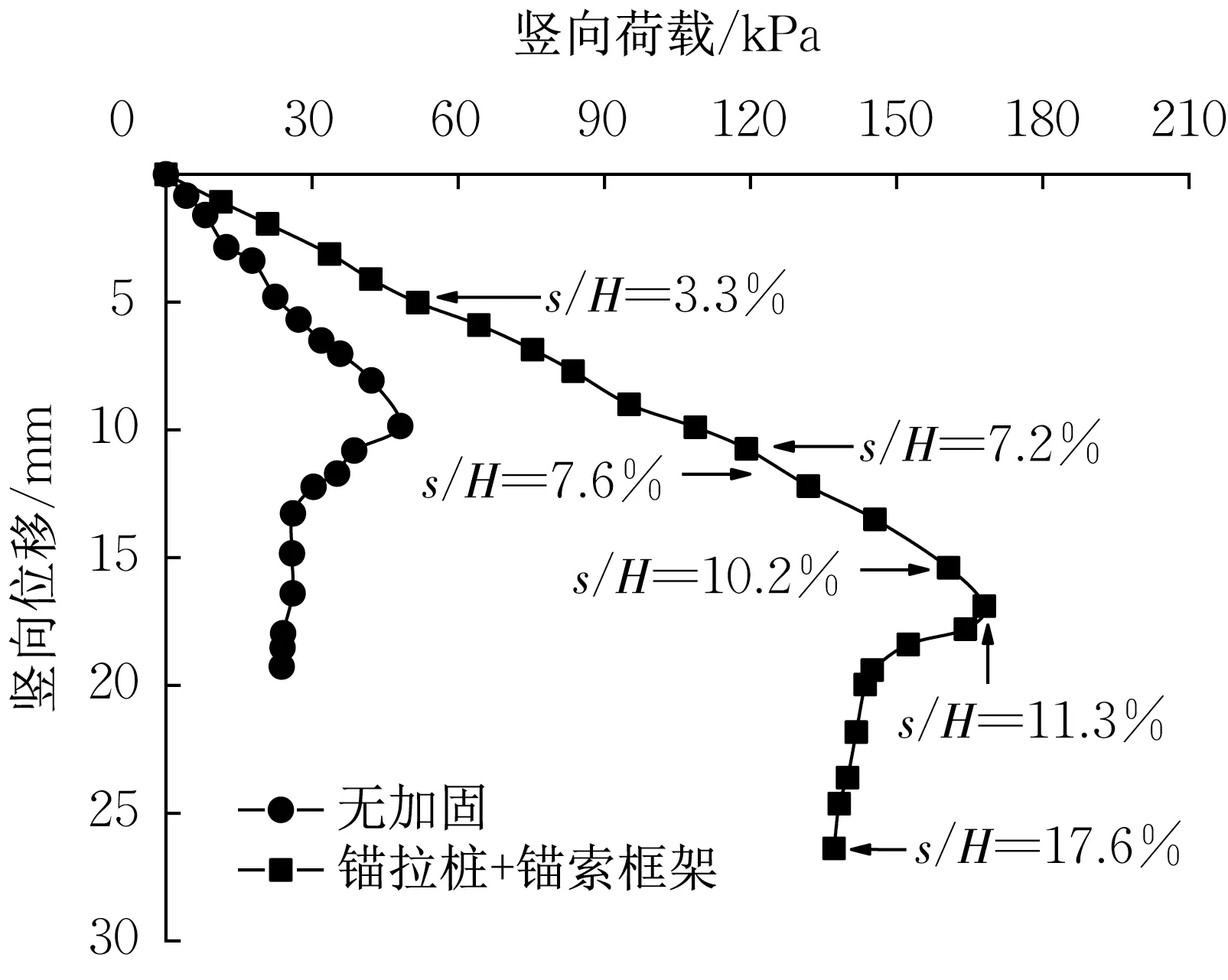
图8 锚拉桩-锚索框架梁加固边坡的荷载-位移曲线Fig.8 Load-displacement curve of slope stabilized with anchored piles and anchor cable frame beams

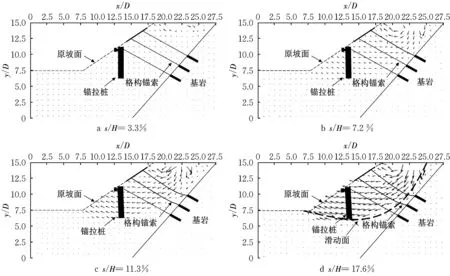
图9 锚拉桩-锚索框架梁加固边坡的位移矢量Fig.9 Displacement vector of slope stabilized with anchored piles and anchor cable frame beams

图10 加载末期锚拉桩-锚索框架梁加固边坡的变形Fig.10 Deformation of slope stabilized with an⁃chored piles and anchor cable frame beams at the end of loading

比较组合结构加固边坡与无加固边坡的变形特征，可见组合结构加固边坡的上部浅层变形明显减弱，说明锚索框架有效解决了坡体浅层变形过大问题。此外，组合结构加固边坡的滑面较无加固边坡变深，这是由于锚索框架和锚拉桩的联合约束作用，使得土体变形向深部发展并最终近水平剪出。

2.3 锚拉桩-锚索框架梁组合结构的锚索轴力变化

图11 为组合结构中锚索轴力随s/H的变化曲线。由图可见，加载初期s/H≤ 3.3 %时，第1、第2排锚索以及锚拉桩锚索的轴力均逐渐增大，但第1排锚索轴力增加速率明显大于其他2 排；加载至s/H=7.6 %时，第1排锚索轴力达到峰值14.8 N，而第2 排锚索和锚拉桩锚索轴力继续增大；加载至s/H=10.2 %时，第1 排锚索轴力越过峰值降至4.9 N，而第2 排锚索轴力达到峰值15.8 N，锚拉桩锚索轴力仍在继续增大；加载至坡顶极限荷载s/H=11.3 %时，第2 排锚索轴力越过峰值降至10.0 N，锚拉桩锚索轴力仍在增大；继续加载至s/H=11.9 %时，锚拉桩锚索轴力达到峰值16.1 N；加载末期s/H=17.6 %时，3排锚索轴力均降至残余值。

图11 锚索轴力随s/H值的变化曲线Fig.11 Axial force of anchor cables versus s/H

锚拉桩锚索轴力变化可反映作用于锚拉桩的荷载变化。在限制边坡变形过程中，坡体上部的第1、第2排锚索框架与坡体下部的锚拉桩结构存在协同受力现象。对于推移式滑坡，在坡顶加荷过程中，从上至下的3排锚索轴力先后达到峰值，其对应的s/H分别为7.6 %、10.2 %和11.9 %。结合图8坡顶荷载-位移曲线，上述坡顶位移对应的坡顶荷载分别为122 kPa、164 kPa 和165 kPa。定义边坡稳定安全系数为坡顶极限承载力与坡顶荷载之比。则第1排锚索失效时，边坡的稳定安全系数为168 kPa/122 kPa=1.38；第2 排锚索失效时，边坡的稳定安全系数为168 kPa/164 kPa=1.02。由此可见，锚拉桩-锚索框架梁组合结构并未在第1排锚索失效时出现“多米诺骨牌”效应，仍具有较高稳定性，需进一步提高坡顶荷载才可使第2 排锚索失效。当第2 排锚索失效时，坡顶荷载接近边坡极限承载力。当第3排锚索失效时，坡顶荷载已衰减至极限承载力以下，边坡处于不稳定状态。

这说明锚拉桩-锚索框架梁组合结构加固推移式滑坡时，3 排锚索共同分担荷载，但最上面的锚索首先发挥作用，承受荷载最大。在其拔出失效后，后面的锚索依次发挥作用直至拔出失效，同时边坡的稳定性逐步降低。因此，目前基于极限平衡理论将所有锚索的极限拉拔力作为抗滑力分量，计算得到的锚拉桩-锚索框架梁组合结构的稳定性是偏于危险的。建议验算锚拉桩-锚索框架梁组合结构加固推移式滑坡整体稳定性时，同时验算最上面锚索的稳定安全系数，使其满足工程所需的安全系数，由此可保证整个加固边坡的稳定性。