一种顾及轨道误差的实时GPS钟差估计方法

谭 粤，黄观文，付文举，王 乐，谢 威，曹 钰

(1. 长安大学地质工程与测绘学院，西安 710054； 2. 武汉大学测绘遥感信息工程国家重点实验室，武汉 430079)

0 引言

实时精密单点定位(Real-Time Precise Point Positioning, RT-PPP)技术因其独特的优势，如可以单站作业、实时性强、模型简单、定位精度高、不受距离的限制等，目前广泛应用于低轨卫星精密定轨[1]、地震监测[2]和实时大气探测[3]等领域。精密的实时卫星钟差产品是支持全球RT-PPP技术的先决条件之一，其精度和稳定性决定了定位服务性能。因此，获得实时、精密和稳定的卫星钟差产品一直是该领域的研究热点[4-6]。国际GNSS服务(International GNSS Service，IGS)实时工作组于2013年4月正式通过实时数据流提供全球定位系统(Global Positioning System，GPS)轨道和钟差改正数。卫星原子钟受限于自身物理特性及太空环境因素，难以用数学模型对钟差进行准确建模预报[7]，实测钟差产品的24h预报精度约为3ns[8]，远低于IGS建议的0.3ns钟差精度。因此，利用地面监测站网的实时观测数据估计卫星钟差是获得实时精密钟差的有效方法。

随机模型作为实时卫星钟差估计数学模型的重要组成部分，其准确性决定了实时钟差估计的精度和稳定性。王浩浩等采用高度角定权模型进行了BDS-2/BDS-3实时卫星钟差估计[9]。赵齐乐等基于高度角定权模型，估计了BDS-2和GPS的实时卫星钟差[10]。Liu T.等把伪距和载波分别为0.3m和0.003m的先验观测值精度加入高度角相关的定权模型中，通过实时数据流解算获得了四系统的实时钟差[4]。谷守周等在进行BDS/GPS实时钟差融合估计时，将定轨时的卫星轨道精度信息加入定权模型中，一定程度上完善了定权模型[11]。刘站科等利用定轨时的卫星轨道精度信息进行了多模GNSS实时钟差融合估计，进一步推广了此定权模型[12]。在实时卫星钟差估计时，大多数钟差估计软件都是直接固定存在误差的预报卫星轨道，采用简单的与高度角相关的定权模型。然而，固定轨道后的残差模型不仅包含了观测误差，还存在轨道误差。不同卫星轨道的精度不同，且随着预报时长的增加而降低。综上所述，只考虑观测值误差和卫星经验定轨误差的定权模型是不完善的，随着钟差估计时间的增加，会对实时钟差估计精度和稳定性造成不利影响。因此，本文基于IGS超快速(IGS Ultra-rapid，IGU)实时轨道文件提供的轨道标准差信息，提出了一种顾及轨道误差的实时GPS钟差估计方法，并设计了两个实验方案验证其有效性。本文首先介绍了实时卫星钟差估计函数模型，详细推导了顾及轨道误差的定权模型。然后，介绍了实验数据、处理策略和数据处理流程，并对实验结果进行了详细分析。最后，给出了本文的结论。

1 实时卫星钟差估计函数模型

本文采用非差无电离层(Ionosphere-Free，IF)组合模型实时估计卫星钟差，GPS单系统实时钟差估计的函数模型如下

(1)

(2)

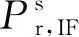
在实时钟差估计时，常固定地面测站坐标和卫星轨道并计算其几何距离，然后从观测方程中移除。传播路径的对流层延迟误差采用经验模型对其干分量进行改正，残差部分首先计算映射函数，然后估计天顶对流层湿延迟。卫星和接收机码偏差通常和相应的钟差参数融合。UPD被相位模糊度吸收。其他误差，如地球固体潮、海洋潮汐和极移潮改正，相对论延迟，相位缠绕，卫星和接收机相位中心偏差和变化等，通过经验模型改正。简化后的函数模型如下

(3)

(4)

本文采用序贯最小二乘平差方法进行实时卫星钟差估计，随着每个历元的测量更新和状态更新，估计的钟差将会逐渐收敛[14]。当先验信息严密可靠时，实时序贯最小二乘估计具有无偏最优性[15]。由于接收机钟差和卫星钟差线性相关，会导致法方程秩亏，因此选择一个参考钟来消除秩亏，计算的钟差都是相对于参考钟的相对钟差[1]。当参考钟的精度优于10-6s时，并不会影响用户的定位精度[16]。

2 随机模型

2.1 基于高度角的随机模型

实时钟差估计随机模型常用高度角相关的定权模型[10,14,17]，具体公式如下

(5)

式中，P表示权值；lc和pc分别表示载波相位观测值和伪距观测值的权；E表示卫星高度角；σ0表示单位权中误差；σlc和σpc分别表示载波相位和伪距观测值的精度。

2.2 顾及轨道误差的随机模型

设卫星位置为(xs,ys,zs)，各分量不相关，其坐标对应的精度为(σxs,σys,σzs)；设测站坐标为(xr,yr,zr)，其位置精确已知。则卫星到接收机的几何距离ρdis计算如下

(6)

由于GPS卫星到接收机的距离在20000km左右，在线性化时可忽略高阶项的影响[18]，只考虑一阶项的误差。把几何距离ρdis在卫星位置初值(xs0,ys0,zs0)进行泰勒一阶展开可得

(7)

式中

dxs=xs-xs0，dys=ys-ys0，dzs=zs-zs0

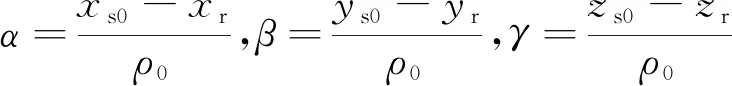
dρsp3=αdxs+βdys+γdzs

(8)

由协方差传播律可得几何距离ρdis的精度为

(9)

综上所述，结合2.1节，顾及轨道误差的定权模型如下

(10)

3 实验分析

3.1 实验数据与处理策略

3.1.1 实验数据及轨道精度分析

本实验采用IGS发布的6h更新的超快速产品IGU轨道综合产品。IGU轨道产品由不同IGS分析中心的超快速轨道综合而来，其中包含了48h的数据，前24h是实测产品，精度较高；后24h是预报产品，其精度随着预报时长增加而逐步降低，尤其是钟差产品[19]。IGU部分产品说明如表1所示[20]。如图1所示，IGU轨道文件中，第1～5列分别是卫星号，X、Y、Z坐标和钟差信息；第6～8列分别是轨道X、Y、Z坐标的标准差，即为内符合精度。假设x为轨道坐标内符合精度表示的数值，那么相应的轨道坐标精度为1.25x，单位mm(https://igs.org/formats-and-standards/)。由于IGU实时轨道的采样间隔为15min，且轨道内符合精度变化缓慢，因此本文通过线性插值得到实时轨道内符合精度信息。

表1 IGS发布的产品信息

图1 IGU 轨道文件中的轨道内符合精度信息(部分)

图2给出了IGU中的部分GPS卫星的轨道外符合精度和内符合精度时间序列，图中外符合精度表示以IGS事后精密轨道为参考得到的IGU轨道误差，内符合精度表示IGU轨道文件中给出的轨道标准差信息，两者都换算成距离表示。从图2可以看出，外符合精度和内符合精度的变化趋势相同。通过相关性分析，G15的相关性高达0.82，G24为0.50，都表现出较强相关。内符合精度信息可以在一定程度上反映出外符合精度，因此采用IGU轨道文件中的内符合精度定权具有一定的合理性。

(a) G15

图3给出了G32卫星在2020年积日(DOY)261的轨道外符合精度和内符合精度，可以看出，G32卫星的轨道外符合精度很差，从相应的内符合精度信息可以反映出来。由上一节提及的轨道内符合精度阈值可知，G32在DOY261天因为内符合精度大于0.06m被剔除。

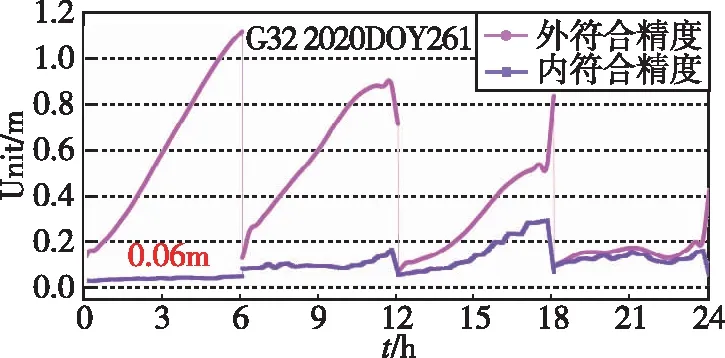
图3 轨道精度阈值

3.1.2 钟差估计策略及精度评定方法

本实验选用全球均匀分布的68个MGEX(Multi-GNSS Experiment)测站。GPS卫星可以被所有的测站实时跟踪。实验采集了2020年9月13～17日，年积日257-261(DOY，Day of Year)的30s采样间隔的实时观测数据，利用事后仿实时估计GPS卫星钟差，其中DOY 257存在钟差收敛过程，故不统计DOY 257的钟差估计结果[14]。

本实验设计了两个方案以验证本文提出的新的钟差估计策略的有效性，方案1：采用常规的高度角相关的随机模型；方案2：采用顾及轨道误差的随机模型。

本文采用团队自研事后仿实时钟差估计软件[14,21]，具体的实时钟差估计策略如表2所示，其中卫星钟差和接收机钟差作为白噪声进行估计，每个测站的天顶对流层延迟采用每小时分段常数估计，模糊度在一个连续的观测弧段内作为常数估计。

表2 实时钟差估计策略

实验数据处理流程如图4所示。首先，对实时观测数据和轨道数据进行数据预处理，得到干净、不含粗差的数据。然后，用线性插值计算卫星的内符合精度，并判断该颗卫星的内符合精度是否满足阈值，如果不满足，则剔除该颗卫星；如果满足，则采用顾及轨道精度定权计算该颗卫星观测值的权值。最后进行实时钟差估计。

图4 数据处理流程图

为了验证本文提出方案的可行性，本文选用IGS事后精密钟差产品评估两种方案的钟差估计精度。IGS事后精密钟差产品由多家IGS分析中心的事后精密产品综合得到，其产品稳定且精度高，精度优于0.02ns，因此可以客观地评估两种方案估计的钟差精度[20]。钟差的标准差(Standard Deviation, STD)可以反映实时估计的钟差精度，这将会直接影响RT-PPP的定位精度[25]。与选取特定卫星钟作为参考钟不同，本文选用虚拟钟(即所有卫星重心基准)作为参考钟，消除不同钟差产品的系统偏差，可以有效避免因为选取了较大误差的特定参考钟计算得到有偏差的STD值[16,26]。

3.2 实验结果分析

假设单位权中误差为伪距观测值精度，即σ0=0.6m，则当高度角大于30°时，方案1的伪距观测值权值为1.0，载波相位观测值权值为90000.0，且一直保持不变。在采用方案2的定权方式后，ABMF测站可观测的部分卫星轨道误差和载波相位观测值的权值如图5所示。从图5(a)可以看出，G32的轨道误差最大；对应图5(b)G32的载波相位观测值权值最小。因此，采用方案2后，当实时轨道误差增大时，对应的观测值权值将会降低，一定程度上纠正了轨道误差大造成的随机模型偏差。

(a) 轨道误差

GPS实时卫星钟差在2020 DOY258-261的平均钟差STD统计如表3所示。从表3可以得出，方案1的所有卫星平均钟差STD为0.086ns，方案2为0.079ns，方案2比方案1整体精度提升了8.1%。在DOY261卫星平均钟差STD提升最大，提升了15.2%。

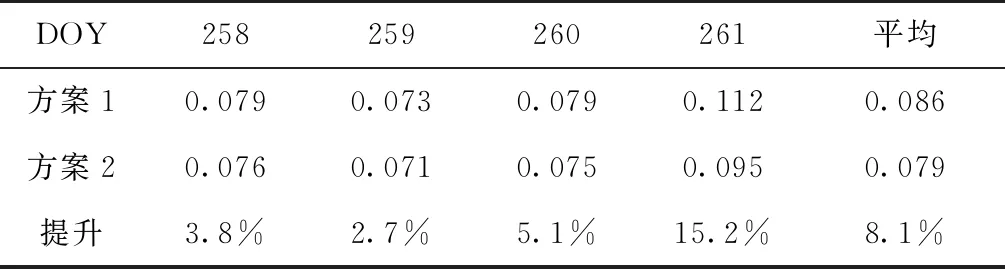
表3 每天钟差平均STD

图6统计了每天所有卫星的钟差STD平均值，可以看出，在前3天(DOY258-260)方案2因为采用了顾及轨道误差的定权模型，改进了目前常用的高度角定权模型，钟差估计精度比方案1都有所提高，平均提高了3.9%；其中DOY260提升较明显，提升了5.1%。图7所示为G19卫星在DOY260的钟差估计误差时间序列，可以看出，方案1的钟差误差波动较大，而方案2在采用新的定权模型后，钟差误差表现平稳，特别是在12点之后；前者的钟差STD为0.075ns，后者为0.036ns，精度提升了52.0%。在DOY261因为剔除了G32一部分轨道预报误差较大的弧段，因此整体的钟差估计精度提升最大，提升了15.2%。

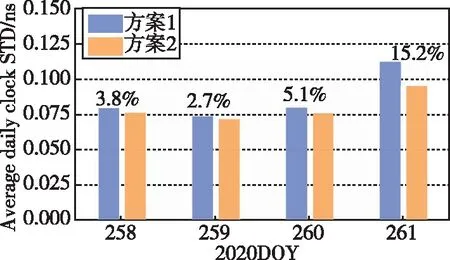
图6 每天的平均钟差STD精度

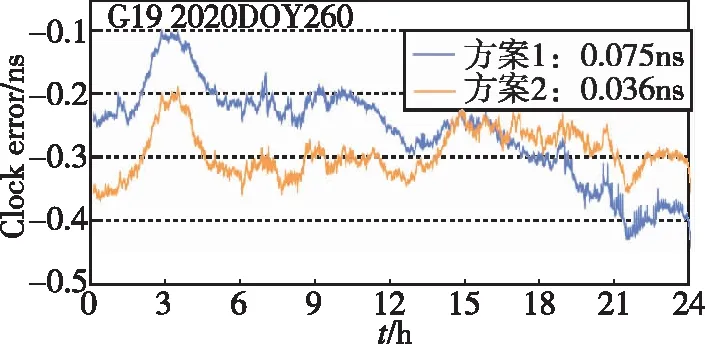
图7 G19卫星在DOY260的钟差误差时间序列

GPS每颗卫星在2020 DOY258-261的平均钟差STD统计如图8所示。其中，由于G32卫星在DOY261的轨道误差很大，采用方案1的钟差估计策略时，G32的平均钟差精度超过了0.25ns，误差较大。在采用方案2后，成功剔除了一部分轨道较差的弧段，使得G32卫星的钟差估计精度维持在正常水平，钟差估计精度提升了48.2%，所有卫星的钟差估计精度都在0.15ns以内。除G32卫星外，其他卫星钟差估计得益于采用了顾及轨道误差的随机模型，钟差估计精度有不同程度的提升，其中G16卫星提升幅度最大，提升了25.7%。由于轨道文件中的轨道精度信息变化相对缓慢，且存在少数卫星的轨道误差增大但是内符合精度变小的情况，如G09和G12等，造成定权模型存在一定偏差，因此有的卫星钟差估计精度有一定降低[27]。特别对于轨道预报精度已经较高的卫星，如G11和G13等，由于实验采用的是模糊度浮点解，钟差估计模型本身存在一定偏差，因此两种方案的钟差精度差异在合理范围之内。但总的来说，钟差估计精度是有一定提高的。

图8 每颗卫星的平均钟差STD

4 结论

本文提出了顾及轨道误差的实时钟差估计策略。首先利用IGU综合轨道的内符合精度信息，通过线性插值得到每颗卫星的实时轨道内符合精度，然后按照一定数学模型将其融入到常用的高度角定权模型中，并根据内符合精度阈值，剔除了轨道内符合精度超限的卫星。研究结果表明：

1)超快速轨道产品中提供的轨道标准差与绝对轨道误差表现出较强相关，把轨道标准差视为轨道误差融入定权模型具有一定合理性；

2)顾及轨道误差的定权模型可以完善常用的高度角定权模型，整体提高了实时钟差估计精度，当卫星轨道预报异常时能有效识别并剔除；

3)与常用的高度角定权模型相比，采用顾及轨道误差建模的钟差估计方法，在2020 DOY258-261，GPS卫星钟差估计精度最大提升15.2%，平均提升8.1%;

4)通过轨道内符合精度阈值成功剔除了一部分轨道较差的弧段，使得G32卫星的钟差估计精度保持在一个正常水平。