基于轨迹拐点滤波的激光雷达里程计定位算法研究

邹筠珍，赵 伟，许舒晨，孙永荣

(南京航空航天大学自动化学院，南京 210016)

0 引言

随着自动驾驶汽车的发展，作为前沿发展技术之一的自定位技术成为一个热门的研究方向，特别是在全球定位系统(Global Positioning System，GPS)拒止环境下的自定位算法是需要研究的重点。近年来，激光雷达里程计(LiDAR Odometry，LO)的应用逐渐兴起，相对于视觉定位来说，激光雷达可以提取到深度信息，同时摆脱了对光照环境的依赖，在车辆定位的应用方面具有一定的优越性。

LO以激光雷达点云信息作为输入，利用帧间匹配实现车辆定位，但是长距离行驶产生累积漂移的问题不容忽视。目前主要有三种解决方式：多源传感器融合、同步构建地图以及利用已有地图进行定位校正。多源传感器融合方式[1-2]虽然定位精度较高，但融合前标定的传感器外参容易受到机械变形及环境影响，数据处理耗时长、操作复杂且成本昂贵[3]。而同步定位与建图(Simultaneous Localization and Mapping，SLAM)方法[4-5]需要进行全局的地图构建并利用回环检测来消除误差[6]，极大地限制了车辆的运行轨迹。利用已有地图进行定位校正方式的低成本、易操作的特点，使得其在解决里程计累积漂移的问题时更具有优势。已有地图主要包括点云地图和路网地图等。点云地图存储需要较大的内存，且没有开源的数据，需要提前构建；相较而言，路网地图例如开放街道地图(OpenStreetMap，OSM)，由于其开源及轻量级的特点，能减少系统所需成本及内存。文献[7]和文献[8]利用OSM路网及建筑信息构建特征描述子，并利用激光点云信息进行定位，但OSM建筑信息及描述子存储增加了额外的内存。文献[9]仅利用OSM路网信息，将里程计与路网数据结合于统一的框架中，利用基于快速定向倒角匹配的蒙特卡罗定位对轨迹的每一帧进行匹配，能在更低内存的情况下达到类似的定位精度，但其在里程计轨迹失真的情况下，效果并不佳。文献[10]利用轨迹与地图进行匹配，依据拐点通过距离阈值约束并选择最佳路线，避免了里程计误差发散，但是对于长路径来说，穷尽搜索会变得极其耗时，而且将原有轨迹固连至路网上将会带来额外的误差。文献[11]和文献[12]在此基础上考虑了路宽的影响，采用多源粒子滤波方法进行轨迹匹配，相对于文献[10]来说误差有了进一步优化，但是以事后推定的方式计算轨迹-路网匹配关系，不具有实时性。不过文献[11]和文献[12]利用拐点进行滤波的思想，极大地节约了定位成本，且达到不错的定位效果，此思想为本文的算法提供了启发。

综合上述分析，本文提出了一种基于路网节点的粒子滤波优化算法，将LO及OSM数据作为输入，并依据轨迹的拐点进行粒子滤波，对LO的累积误差实现有效的抑制，在满足校正精度的同时避免频繁使用滤波器，且可以满足系统的实时性要求。

1 基于路网节点的粒子滤波系统框架设计

本文选用LeGO-LOAM的前端[13]作为LO，平面点和边缘点作为激光雷达点云图像中显著的特征点，可以通过曲率的大小对其进行分别提取，并进行特征匹配，实现实时定位。但是在没有回环检测等后端处理的情况下，不可避免地会出现误差逐渐发散。为了补偿LO随着时间推移而积累的漂移，本文使用轻量级地图OSM以及轨迹拐点信息对LO定位误差进行校正，基于路网节点的粒子滤波系统的结构框架如图1所示。

本系统主要包含三部分，分别是利用LO获取位姿、拐点提取及匹配和利用粒子滤波器对拐点进行定位校正。首先，将LO的位姿作为运动方程对粒子进行预测；同时利用航向角信息对运动轨迹进行拐点提取，并与OSM地图节点进行匹配；然后，当拐点被提取出来后，根据其与地图节点的匹配程度更新粒子权重实现滤波，获得粒子的新位姿；最后将其均值作为车辆的真实位姿，实现误差校正，其中拐点提取及匹配和利用粒子滤波器对拐点进行定位校正是本文的研究重点。

2 基于路网节点的粒子滤波优化算法研究

2.1 轨迹拐点提取及匹配

轨迹拐点是粒子进行权重更新的依据，拐点提取与匹配的正确与否很大程度上决定了LO定位优化的好坏。为了避免漏检及错检的情况发生，本节利用航向角变化速率、轨迹的直曲比及转角变化约束进行拐点提取，保证拐点提取的可靠性，并将提取的拐点与路网节点进行匹配。拐点的提取主要包括粗筛和精筛两个步骤。

1)拐点的粗筛：在拐弯处，航向角变化比较明显，会出现连续段航向角变化速率较大的情况。故设置阈值θt与帧数m1，当存在连续m1帧以上的航向角速率大于θt时，则认为出现拐弯情况，以航向角速率最大的点作为拐点。为了避免出现拐弯处提取不完整，或者在同一个拐弯处提取出多个拐点的现象，如图2(a)所示，本文对拐弯结束处的终止条件进行优化，认为拐弯结束处需满足连续若干帧(m2)对应的角速率小于阈值θt。通过此法可以将拐弯处轨迹全部提取出，如图2(b)所示。

(a) 原提取效果

2)拐点的精筛：通过航向角速率变化提取出的拐点并不可靠，在直线段行驶时也可能出现上述情况(例如：超车、急刹车等)，为了去除此类伪拐点，需要对其进行精筛。本文采用轨迹的直曲比及转角变化[14]进行判别实现拐点的精筛。某次粗筛结果如图3中黑框所示，设定直曲比阈值S1和角度阈值β1，只有当同时满足直曲比小于S1和转角变化大于β1时，才认为此为拐点，否则认为是伪拐点进行去除，从而达到精筛的目的，精筛结果如图3中蓝框所示。

图3 精筛后提取出的拐点

提取出拐点之后，需要将此点与路网节点进行匹配，遍历路网节点，利用两相邻拐点间长度误差阈值LT及角度误差阈值θT约束获取匹配候选集P。

2.2 基于拐点的粒子滤波算法研究

为了解决LO误差漂移问题，本文基于粒子滤波器框架[15-16]，提出了一种新的粒子权重模型，并于拐点处更新粒子权重。每一次拐点滤波都会校正相应位姿，进而抑制LO误差发散，具体的算法流程如下：

(1)粒子初始化

假设已知小车初始位姿，选定粒子数N，将粒子分布在初始位姿附近，其分布符合高斯正态分布，每个粒子代表小车可能的位姿，初始权重均为1/N。

(2)预测阶段

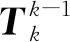
根据运动模型，小车从k-1帧到k帧位姿变化可表示为

(1)

(2)

(3)

(4)

(3)测量阶段及粒子权重更新

粒子滤波算法通过不断更新粒子的位姿及权重来近似系统的真实后验概率，通过运动模型，粒子的位姿获得更新，相应权重由测量模型更新。与传统的粒子滤波不同的是，本算法不对每个位置进行测量及粒子权重更新，只对位于拐点处的粒子进行处理，这样在保证定位精度的同时，也可以提高效率，保证实时性。

通过2.1节中的方法进行拐点的识别及匹配，可获得候选匹配集P。如图4所示，P点集可能不止一个点，为了避免错误的拐点数据关联导致定位误差加大，本文不直接进行数据关联，而是利用不同节点的相似度模型及测量值作为粒子权重的更新依据，提出了一种新的粒子权重模型如下

图4 候选匹配集P

(5)

受到文献[11]和文献[12]的启发，本文轨迹与道路候选段相似度模型ω1构建如图5所示。

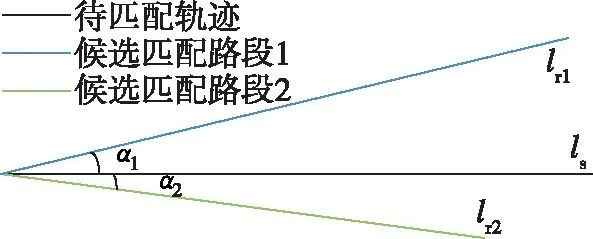
图5 相似度模型

轨迹的相似度模型主要基于长度误差及朝向角误差，其中相对长度误差和朝向角误差分别为

(6)

α=|αs-αr|

(7)

构建的相似度模型为

(8)

其中，λ为归一化权重因子，其值介于[0,1]之间，其大小表征了相似度模型对长度相似度和角度相似度的依赖程度。通过此模型可以看出，当轨迹与道路候选段相似度越高，ω1的值会越大。

基于测量值的概率密度函数ω2的构建方式如下

(9)

d′的表达式为

(10)

其中，μd为0，d代表粒子与路网节点的距离，即测量值，如图6所示，dth为设置的距离阈值，旨在考虑到路宽因素的影响。即认为在一定范围内(d≤dth)，粒子的可靠性相同且最高，当超过一定范围时，认为粒子与路网节点越远，粒子越不可靠。

图6 粒子与节点分布

根据式(5)可以看出，粒子的权重是由相似度模型及测量值联合决定的，当LO获得的轨迹与某一道路候选段相似度越高，则表明拐点与匹配集P中对应节点关联程度越大，故距离此节点测量值越小的粒子理论上应该拥有更大的权重，而此次构建的粒子权重模型很好地实现了这一点。

(4)重采样

为了避免粒子退化，需要进行重采样操作，根据权重比例复制粒子，在这一过程中，权重较大的粒子将保留，权重小的粒子会舍弃。将得到的新粒子集代入状态转移方程中，对其进行预测和测量，反复迭代，并将每次获得的粒子集均值作为轨迹校正后的位姿输出。在每确定一处拐点后，再依据路网中边的朝向信息对粒子进行方向约束，此优化算法可以有效减小LO带来的定位误差，实现小车准确定位。

3 实验结果与分析

本章设计了相关实验以验证本算法的有效性，选用公开数据集KITTI[17]，激光雷达型号选用Velodyne HDL-64E，水平分辨率为0.2°，频率为10Hz。其中序列00-10由GPS/IMU进行标定并作为真实位姿，本文选用序列00、02、05、08进行实验，各序列的OSM地图于OpenStreetMap官网下载，并进行节点标定。

在本次实验中，选取的角速率θt为0.01(°)/帧，直曲比S1为0.998，角度阈值β1为15°，角度阈值θT为25°，长度阈值LT为0.3，选取高斯预测噪声[vxk,vyk,vzk,vγk,vθk,vφk]T标准差为[0.2,0.2,0.2,0.005,0.0005,0.0005]T，均值为[0,0,0,0,0,0]T，归一化权重因子λ为0.5，选取的粒子总数N为300个。

(1)算法耗时分析

不同的粒子数目对算法的准确性和运行效率存在影响。当粒子数量越多，准确性提高，算法耗时也会随之增加。为了平衡两者，需要通过实验确定最佳粒子数N。某次实验中粒子数量与均方根误差(Root Mean Squared Error，RMSE)及算法耗时如图7所示。其中，均方根误差用来表征算法的准确性，算法耗时选取本次实验中粒子滤波的最长耗时。

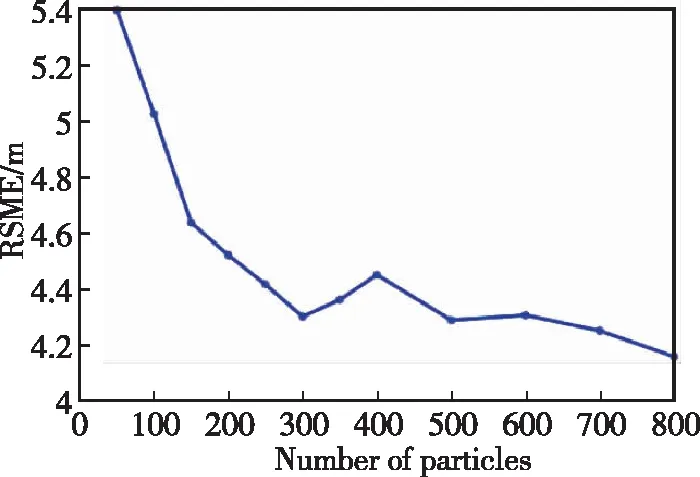
(a) 算法误差与粒子数关系

通过图7可以看出，当粒子数N小于300时，误差变化较大，当N大于300时，耗时增加明显，故选取最佳粒子数N为300。此时，误差为4.30m，粒子滤波最大耗时为12.9ms，只在LO运行时间上增加了很小的成本，可以满足系统的实时性要求。

(2)本算法与LO定位结果比较

由于高斯预测噪声随机，每次通过粒子滤波得到的轨迹略有不同，本次对每个KITTI序列进行50次实验，计算每一次实验轨迹的均方根误差，取50次实验的均值结果如表1所示。

表1 KITTI序列算法对比

通过表1的实验结果可以看出，本算法能有效抑制LO的误差漂移，定位误差均明显减小，其优化程度主要和拐点数目、路况、行驶距离和原LO误差等有关。由于序列KITTI05的拐点数较少，其优化程度较低，而序列KITTI08行驶距离较短，拐点多，优化程度较高。

将算法前后的轨迹及误差进行对比分析，以序列KITTI00为例的滤波前后的结果如图8所示。

由图8(a)可以看出，经过本算法校正后的轨迹分布在路网周围，与真实轨迹有较高的重合度，定位轨迹的误差存在明显的改善；由误差曲线图8(b)可以看出，LO的误差会随着时间逐渐发散，而本算法由于拐点的约束，每经过一处拐点，误差都会得到校正，最终输出误差持续较低，显著地解决了LO的累积误差过大的问题。

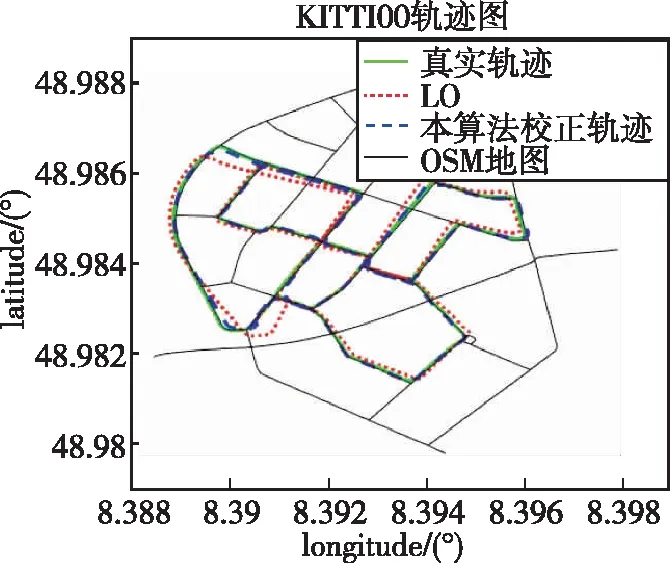
(a) 序列KITTI00滤波轨迹对比图

(3)与其他粒子滤波算法比较

为了说明本算法的定位效果，选取文献[11]中算法进行对比。文献[11]提出了一种拐点滤波(Turning Point Filtering，TPF)算法，通过相邻点关系约束拐点与路网节点的匹配关系，并使用多源粒子滤波算法实现里程计误差校正。选用同样的参数进行50次实验，得到的误差结果如表2所示。

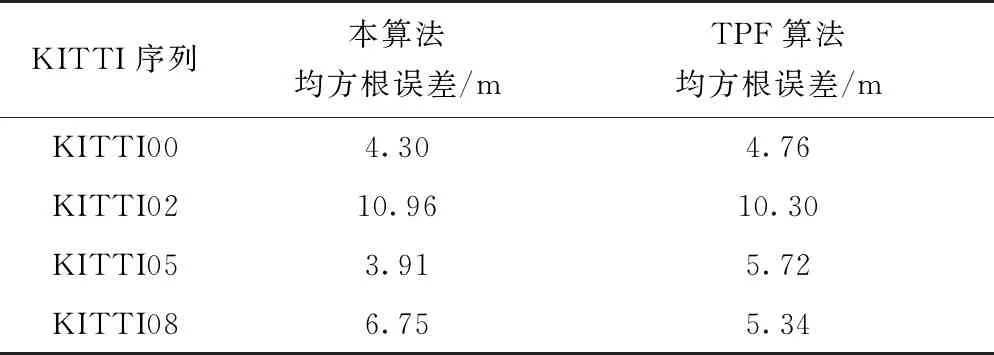
表2 KITTI序列优化算法对比

可以看出，本算法与TPF算法得到的误差结果相差不大，但是由于TPF算法是通过事后推定的方式计算轨迹-路网匹配关系，优化定位误差，不具有实时性；而本算法是基于实时定位的，相对于TPF算法来说，本算法具有更广的应用空间。某次实验结果如图9所示。

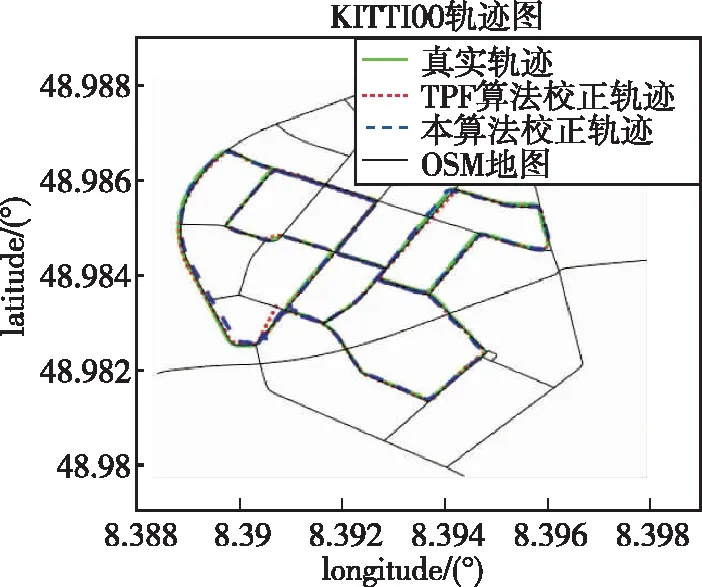
(a) 序列KITTI00轨迹对比图

4 总结

本文针对GPS拒止环境下车辆自定位问题，提出了一种基于路网节点的粒子滤波优化算法，该算法基于粒子滤波框架，在运动过程中对粒子进行状态预测，并于拐点处对粒子权重进行更新以校正位姿，消除激光雷达带来的累积误差。通过对KITTI数据集的实验可以看出，本算法具有显著的优化效果，可以避免LO在长距离定位中带来的漂移。本文的主要结论如下：

1)对于拐点的提取，采取两次筛选，利用航向角变化速率、轨迹的直曲比及转角变化约束进行拐点提取，避免出现拐弯处提取不完整，对直线段的伪拐点进行了较好的去除。

2)基于不同节点的相似度模型及测量值，设计粒子滤波的权重模型，此模型可以针对候选匹配集为多个节点的情况，避免拐点与节点的错误关联导致定位误差加大。

3)在LO的基础上，借助OSM地图，对其进行基于轨迹拐点的粒子滤波，消除激光雷达带来的累积误差。整个过程中没有对每一帧进行粒子滤波，节省了短时间内几乎无法获得额外有效信息带来的运行成本，同时保证了校正的模糊性，具有较好的定位精度和实时性。