一种基于灰色预测理论和抗差自适应Kalman滤波的滑坡监测算法
2023-03-09王建国
杨 旭,杨 旭,李 佳,王建国
(1.北京航空航天大学电子信息工程学院,北京 100089;2.北京航空航天大学合肥创新研究院,合肥 230000)
0 引言
山体滑坡灾害具有隐蔽性强、突发性强、破坏力大的特点。传统的山体滑坡监测方法主要有宏观地质观测法、简易观测法、设站观测法、仪表观测法等,它们普遍存在的问题是需要人工定期到现场进行数据的采集,缺少实时性,监测精度较低,并且对滑坡的预测预警能力差[1-3]。
近年来,在地质形变监测技术不断发展和完善的过程中,大地精密测量法、全球卫星导航系统(Global Navigation Satellite System,GNSS)高精度地质形变监测法、近景摄影测量法、时间域反射测试技术、遥感监测技术等方法常被用于地质形变监测中。目前主流的山体滑坡监测方法是通过合成孔径雷达(Synthetic Aperture Radar,SAR)技术进行监测,但是该方法受天气状况和植被覆盖的影响大,实时性差,难以实现长期监测[4-6]。
实时动态(Real-Time Kinematic,RTK)技术可实现实时定位,并且在静态情况下的定位精度可达mm级。与传统GNSS形变监测技术相比,RTK定位技术具有十分显著的优势。RTK技术被广泛应用于安全监测、土地勘探、城市布局、水利等领域[7-11]。在我国的金川二矿区地裂缝[9]、黄土坡临江I号崩滑体[10]等地质灾害的变形监测中,均采用了高精度的全球定位系统(Global Positioning System,GPS)静态相对定位技术,监测精度可以达到mm级;并逐渐开始尝试采用GPS定位技术监测滑坡体的垂直形变,发现在基线较短、观测时间较长和观测条件较好的情况下,其精度也可以达到mm级[11]。
作为形变监测中的重要数据处理算法,Kalman滤波算法广泛地应用于建筑、桥梁、地质灾害的形变监测中,并取得了非常不错的监测效果[12-15]。C.D.Ince等通过GPS定位技术和Kalman滤波方法对土耳其的伊斯坦布尔和马尔马拉进行形变监测,并取得预期的监测效果[12];朱建军等使用变形监测数据通过Kalman滤波模型动态分析链子崖危岩体位移变形规律[13];高雅萍、张勤使用自适应Kalman滤波在地理信息系统(Geographic Information System,GIS)滑坡监测中也取得了预期监测效果[14]。
影响山体滑坡的因素复杂多变,有已知因素和未知因素,具有典型的灰色特征。灰色预测理论在解决信息不完全的系统问题时具有十分显著的优势。对于具有这样特征的系统,可使用灰色预测理论对其进行深入的分析[16-19]。李晓鸽采用灰色预测理论对鲁地拉水电站对外交通公路滑坡监测数据进行了拟合和预测研究,得到了很好的预测效果[16];王旭昭等使用改进的灰色预测理论对新滩滑坡和黄茨滑坡进行预测分析,取得了良好预测效果[17];此外,K. Yin[18]、王东岳[19]等均使用灰色预测理论进行了山体滑坡预测,并取得良好预测效果。
针对当前的山体滑坡监测技术精度低、实时性差、缺少完善的预测预警机制的问题,本文提出了一种基于抗差自适应Kalman滤波和灰色预测理论的山体滑坡监测技术。该技术通过抗差自适应Kalman滤波进行包括RTK定位技术、土工带传感器技术、无人机近景摄影测量技术在内的多源数据融合,然后通过灰色预测理论与蠕变切线角判据实现对山体滑坡的预测预警功能。
1 抗差自适应Kalman滤波
1.1 抗差自适应Kalman滤波[12-15]
在目标系统中,设Xi为由一组随机变量组成的向量,称为该系统在i时刻的状态向量;设Zi为由一组观测变量组成的向量,称为该系统在i时刻的观测向量。当目标系统为离散时间系统时,系统的状态向量随时间的变化规律可以通过状态方程描述,目标系统的状态向量和观测向量的关系可以通过观测方程描述
(1)
其中,Xi-1、Xi分别是目标系统在i-1和i时刻的状态向量;Zi是目标系统在i时刻的观测向量;U称为控制向量;W称为系统动态噪声向量;V称为系统观测噪声向量;A称为系统从i-1时刻到i时刻的状态转移矩阵;B称为控制向量系统矩阵;H称为观测值系统矩阵。
抗差自适应Kalman滤波技术将抗差估计和自适应估计相结合,以减小观测误差和系统建模误差对滤波结果的影响,其技术原理可以通过如下方程加以描述:
时间更新方程
(2)
Pi/i-1=APi-1/i-1AT+Q
(3)
状态更新方程
(4)
(5)
(6)

1.2 观测噪声等价协方差矩阵的构造
典型的观测噪声等价协方差矩阵D的构造方法[14]有:Huber构造法、丹麦法、IGG法、抗差贝叶斯估计法等。本文选用IGG1构造法,具体内容如下
(7)
其中,一般取k0=2.5,k1=3.5。Vi为观测残差,表达式如下
(8)
1.3 自适应因子的构造
本文采用两段函数模型[14]进行自适应因子的构造
(9)
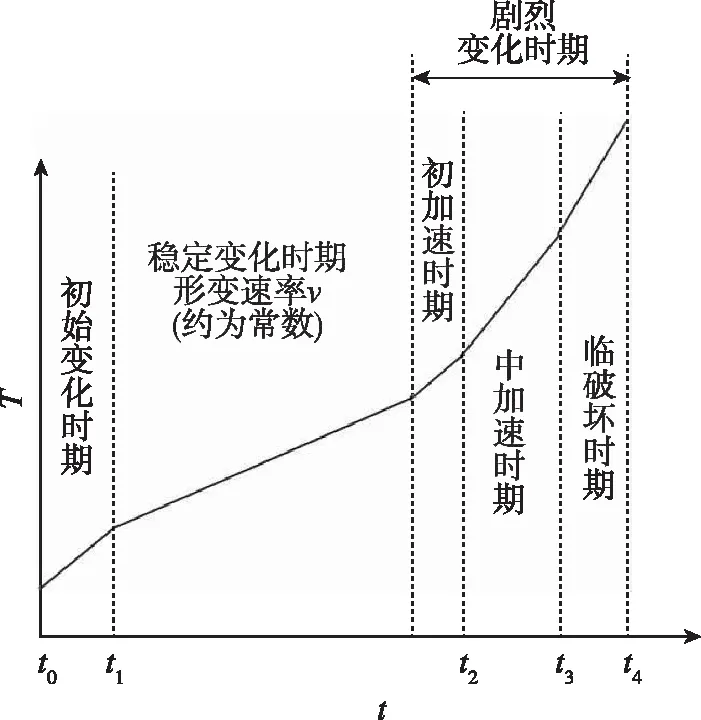
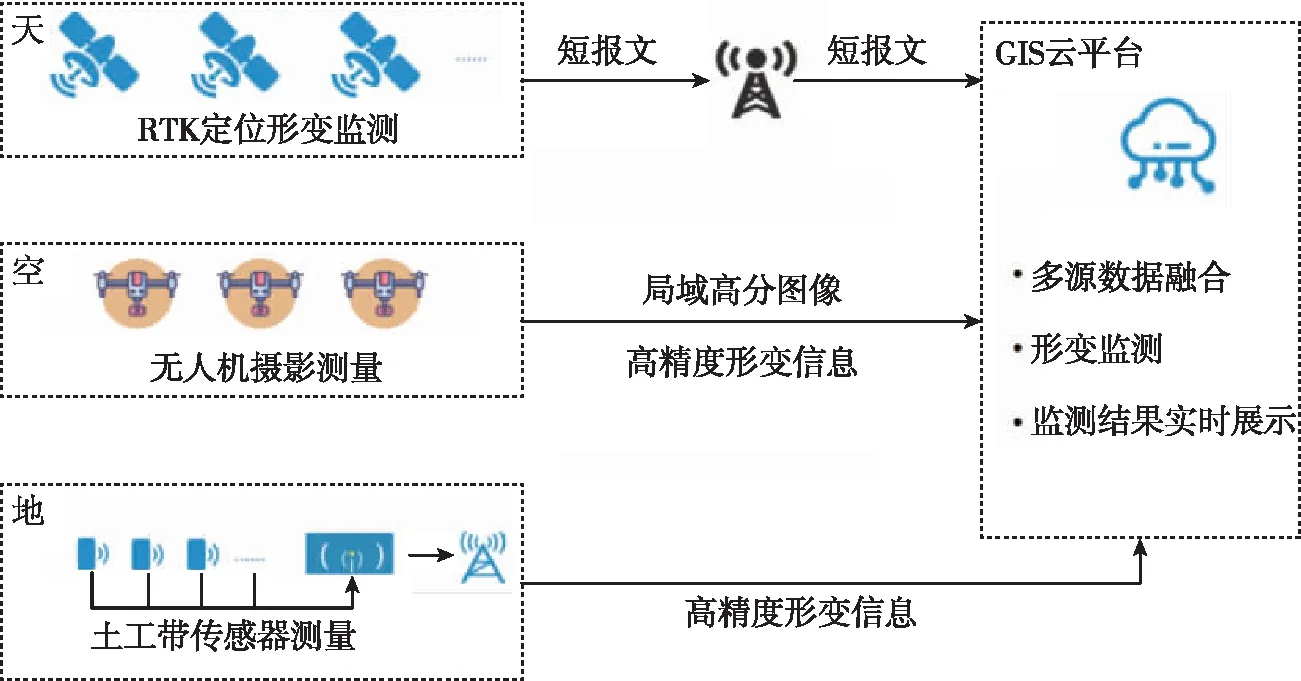
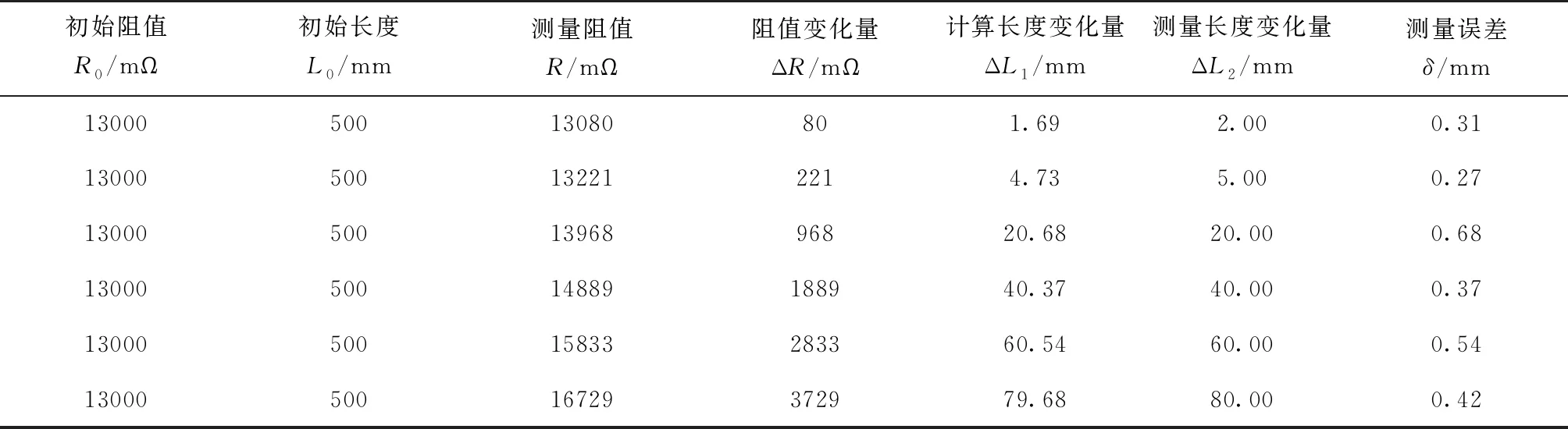
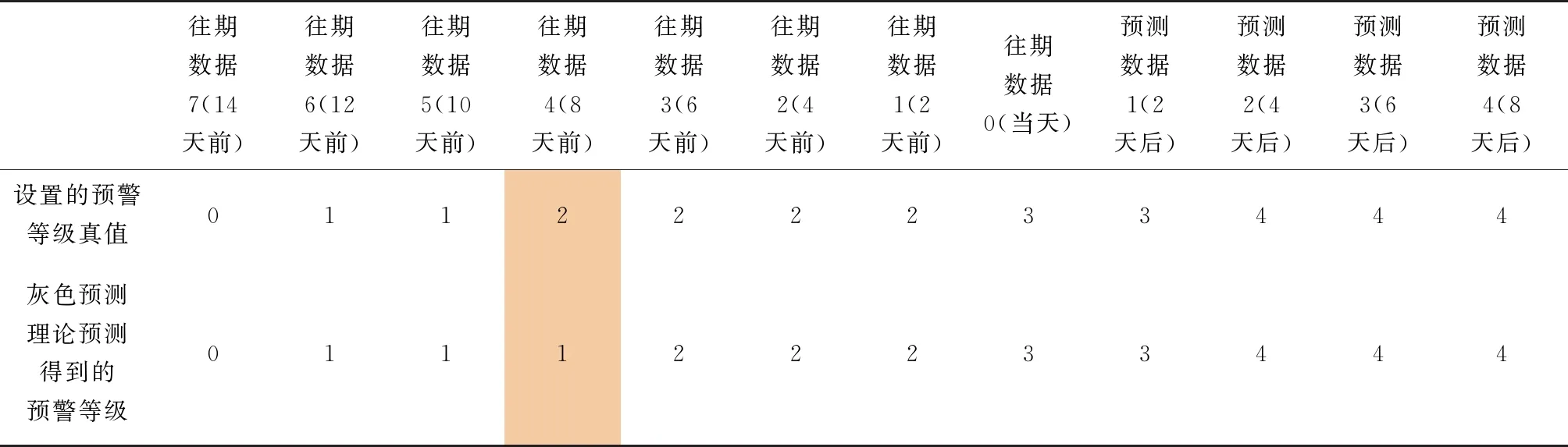
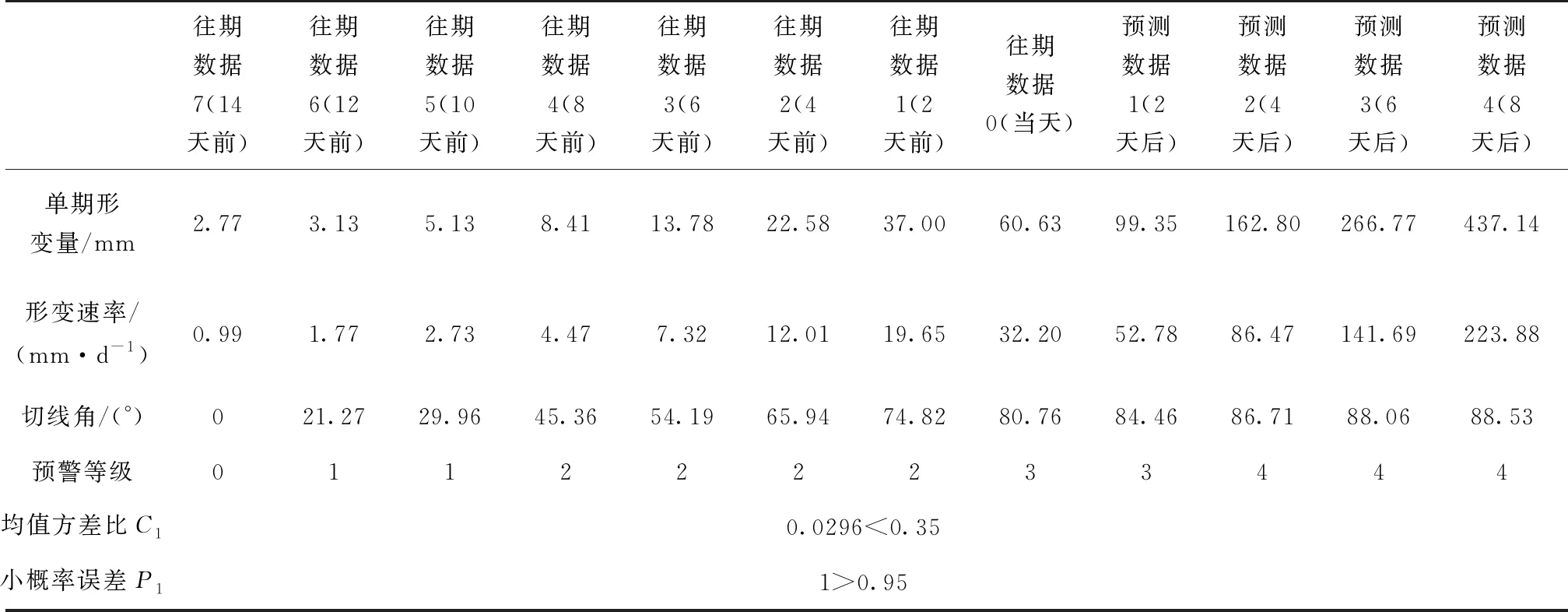
式中,c为常量,一般取c=1~2.5,0 2.1.1 基本GM(1,1)模型 设X(0)为含有n个元素的序列,其中x(0)(k)≥0,k=1,2,…,n。上角标处括号内的数字为序列模型的阶数,第二个括号内的数字为序列中元素的序号。对序列X(0)进行一次累加生成得到它的1-AGO序列X(1)。对序列X(1)进行一次紧邻均值生成得到序列Z(1)。称方程x(0)(k)+ax(1)(k)=b为GM(1,1)模型。其中a为发展系数,b为灰色作用量。令 (10) Y=[x(0)(2),x(0)(3),…,x(0)(n)]T (11) (12) 则有 (13) 方程x(0)(k)+ax(1)(k)=b的解 (14) 取x(1)(0)=x(0)(1),则 (15) 2.1.2 新陈代谢GM(1,1)模型 (16) (17) 在实际应用中,根据实际情况设定阈值A0,当A (18) 在实际应用中,根据实际情况设定阈值P0,当P>P0时,则认为该模型为小概率误差合格模型。关于均值方差比阈值A0和小概率误差阈值P0的设定准则与模型精度等级的关系如表1所示。 表1 模型精度等级参考[19] 通过大量的山体滑坡实例可知,山体滑坡的形变过程可分为3个时期:初始变化时期、稳定变化时期和剧烈变化时期。剧烈变化时期进一步细分为:初加速时期、中加速时期和临破坏时期[19,21-22]。如图1所示。 图1 山体滑坡演化过程中的形变曲线 本文基于上述分析建立蠕变切线角预警判据[20]。通过一定时间的观测得到稳定变化时期监测点的形变速度v0,将稳定变化时期的山体形变运动看作是匀速运动,可知v0是定值,定义 (19) 其中,S(k)为从起始监测时刻到当前监测时刻监测点处的累计位移量;T(k)为具有时间量纲的纵坐标值。由T(k)和t(k)绘制T-t曲线,如图2所示,通过T-t曲线可以得到切线角的表达式 图2 经过处理后得到的T-t曲线 (20) 其中,αk为切线角;t(k)为第k个监测时刻;Δt为采样时间间隔。 根据行业内的长期观测研究得到山体滑坡过程的预警判据表,如表2所示。该预警判据表综合考虑了山体滑坡监测点的形变速率V和切线角α包含的信息内容,对山体滑坡预警等级进行了5层划分,分别代表不同的山体滑坡可能性和危险性,从而实现对山体滑坡的等级预警功能。 课文大意:《综合英语》第四册中第七单元the Monster是一篇典型的描写文,栩栩如生地刻画了十九世纪德国剧作家瓦格纳的人物形象。作为剧作家,瓦格纳是一个天才,毕生创作十三部歌剧和音乐剧,其中十一部仍继续上演,八部被列入世界音乐名剧之列。但现实中,瓦格纳可以称得上是一个怪物,他病态,神经质,喜欢妄自尊大,丝毫不具责任感,喜新厌旧,甚至偷人妻子,赖账不还。(张伊娜,216)这就是本文的主人公,一个集所有缺点于一身的怪物,同时他又是音乐界的天才,具备超凡的禀赋。作者这种先抑后扬的写法极好地刻画了这个杰出的人物。 表2 山体滑坡预警判据表[20] 本文构建以RTK为核心的空天地一体化立体监测网络,实现对滑坡灾害的监测评估。 滑坡监测系统如图3所示,使用RTK进行地质沉降监测,在监测区域布置土工带传感器,采集监测区域的位移信息并上传到云端以待处理,利用无人机摄影测量技术提供空域增强信息,辅助RTK进行滑坡形变监测。北斗短报文通信技术可以实现全天候、全覆盖域、高可靠性的通信,其通信时延约为0.5s,点对点通信时延约为1~5s,同时该技术的设备成本低,适用于广泛的环境监测活动,所以RTK形变监测信息通过北斗短报文进行传递。 图3 山体滑坡监测系统 设计后处理轨迹平滑算法剔除异常测量信息,使用数据融合[23]技术对RTK定位数据、土工带传感器数据、无人机三维成像数据进行综合分析后,在滑坡监测点处计算得到位移、速度、加速度测量信息。本文选用抗差自适应Kalman滤波技术实现数据的融合分析,获得精确的形变监测结果。在获得经过融合处理的形变监测数据后,通过灰色预测理论对未来时刻的形变数据进行合理预测,得到未来时刻监测点处的形变信息,最后结合蠕变切线角判据实现对山体滑坡灾害的预测预警功能。 设备布设的具体情况如图4所示。在重点监测区域进行监测设备布设时,为合理兼顾设备成本和监测效果,主要将监测设备布设在可能滑坡体的顶部和底部,尤其是一些裂缝处。考虑到皖南山区植被覆盖程度大、连续性强,植被覆盖断裂痕迹处也需重点布设监测设备。RTK接收机安置在网络的中心位置。该土工带传感器与RTK接收机的排布网络与无人机摄影测量得到的形变监测数据相结合,三种形变监测数据在空间上具备了数据融合的条件。 图4 监测区域数据采集设备布设 对山体滑坡进行监测分析时,监测点的形变可以使用运动模型进行分析。运动模型的描述方程如下 (21) (22) 位移x(i)通过土工带传感器直接测得 x(i)=dLtu(i) (23) (24) 加速度a(i)通过定期无人机摄影测量形变量和飞行间隔时间计算得到 (25) 为保证监测系统的实时性,在平稳形变阶段,监测区域加速度信息基本稳定,无人机摄影测量周期TUAV可设置较大,TUAV≈30d≈15T。在加速形变易发生滑坡阶段,应按照实际情况进行调整,对于监测价值极高的区域,无人机摄影测量周期TUAV需大幅缩短;对于监测价值一般的区域,可屏蔽无人机摄影测量数据,仅仅使用土工带传感器测量数据和RTK接收机测量数据进行重点监测,此时将加速度信息作为一种随机噪声进行处理。在损失一定监测精度的情况下降低监测成本。 4.3.1 RTK定位数据 RTK定位数据包含RTK接收机的经度、纬度、天线高度、接收机的工作模式和观测卫星数量等信息。通过RTK定位得到监测点的经度、纬度和天线高度,则监测点位移量dLRTK与竖直位移量dL1和水平位移量dL2满足如下关系 (26) dL1=H1-H2 (27) (28) 其中θ1、φ1分别为在起始时刻监测点的经纬度;θ2、φ2为在观测时刻监测点的经纬度;R为地球半径,取平均值6371km。 已知目前RTK接收机动态定位精度可达cm级,平面精度最高可达1cm,高程精度可达2cm。观测时间足够长的情况下,RTK接收机的静态定位精度可达mm级,平均误差在1~2mm。考虑到山体滑坡在平稳形变时期形变速度极为缓慢,因此对于RTK接收机而言可以视为静态定位,形变监测精度可达mm级,使mm级的数据融合具有可行性。 4.3.2 土工带传感器数据 基于土工带电阻值计算其形变量dL的计算公式如下 (29) (30) 式中,R(mΩ)是土工带在观测时刻的电阻测量值;R0(mΩ)是土工带在布置完成时的初始电阻值;L0(mm)是土工带在布置完成时的初始长度;k是比例系数;T(℃)为土壤温度。 因为土工带排布网络的相对尺寸较小,所以忽略山体凹凸性,在对一套监测设备进行分析时,可以看作将土工带排布网络安置在监测点处的切平面上。土工带传感器排布方式如图5所示。10条土工带分成纵横两组,各有5条土工带。每一条土工带上有10个土工带传感器。10条土工带按照网格状排列,空心点是土工带传感器,实心点是2个土工带传感器重合点,RTK接收机安置在网络的中心位置。 图5 土工带传感器与RTK接收机的排布网络 在山体上布设土工带排布网络时,使方形网络的一边沿山体等高线,该方向定义为横向;2个临边垂直于山体等高线,该方向定义为纵向。对土工带数据进行中值滤波和平滑处理后得到监测点的横向位移x和纵向位移y,则由土工带传感器测得的监测点的形变量dLtu为 (31) 土工带传感器测试设备如图6所示,测试结果如表3所示。测试结果显示,土工带传感器的形变监测数据可以达到mm级的监测精度,为高精度地质形变监测提供了可能,使mm级的数据融合具有可行性。 图6 土工带传感器地质采集设备 表3 土工带传感器设备测试 4.3.3 无人机摄影测量数据 通过无人机近景摄影测量技术[24-25]获得监测区域的三维点云数据和倾斜摄影处理结果。使用ArcMap对多期测量数据中的影像控制点进行匹配后,在某一期的三维模型中加入另一期的相对三维模型,计算出前后两期摄影测量中滑坡监测点处的形变量dLUAV,并获得形变区域的位置和大小。目标区域的数字高程地图(Digital Elevation Map,DEM)和数字水平地图分别如图7和图8所示。无人机摄影测量技术的引入,在提供形变监测信息的同时,还提供了地形地貌、建筑分布、交通情况等诸多信息要素,直观地提供滑坡监测点的位置信息,有利于灾害防治工作。 图7 数字高程地图 图8 数字水平地图 以大疆精灵Phantom无人机摄影测量为例,像元大小为2.41μm,相机焦距为8.8mm,飞行高度约为36.5m时,可以满足客户1cm的监测精度要求,如图9所示。考虑到在平稳形变阶段TUAV≈30d≈15T,所以在进行数据融合计算时,由无人机摄影测量得到的形变信息dLUAV的精度在1mm内,在尺度与分辨率方面与土工带传感器形变量dLtu和RTK测量形变量dLRTKmm级精度保持一致。 图9 无人机摄影测量精度分析 本文按照已知的数据内容和格式,综合考虑典型案例中山体滑坡发生前后的形变规律,对数据进行模拟设置。基于模拟设置的警报级别滑坡监测数据对本文的数据处理算法进行仿真分析。最后通过对比模拟设置数据与算法处理结果,检验山体滑坡形变监测数据处理算法的功能。详细分析内容如下,主要包括警报级别数据模拟设置、抗差自适应Kalman滤波融合结果分析、基于灰色预测理论和蠕变切线角判据的预测结果分析、抗差自适应Kalman滤波算法对预测结果的影响分析4个方面的内容。 5.1.1 Kalman滤波效果展示数据模拟设置 为直观清晰地展示通过抗差自适应Kalman滤波算法进行数据融合的效果,本文模拟设置某期采集到的500条土工带传感器形变数据和500条RTK接收机形变数据,模拟设置无人机摄影测量到的滑坡监测点的加速度信息,将模拟数据代入抗差自适应Kalman滤波算法中进行数据融合。数据模拟设置如表4所示。 表4 抗差自适应Kalman滤波数据模拟设置说明 5.1.2 警报级别数据模拟设置 为了检验滑坡监测算法在预警等级为警报等级时的监测效果,按照处理算法的结构并综合考虑典型案例中山体滑坡发生前后的形变规律模拟出12期的数据进行仿真分析,前8期的数据为测量模拟数据,实现对第9、10、11、12期数据的预测和危险等级预警功能。警报数据模拟设置说明如表5所示,数据模拟结果如表6所示。 表6 警报级别数据模拟设置结果 上述内容已经说明每隔2d采集500条土工带传感器和RTK接收机的监测数据。针对每一期的大量监测数据,本文结合无人机近景摄影测量计算得到的监测点加速度信息,使用抗差自适应Kalman滤波进行数据融合,最终得到监测点处精确的形变量,为实现后续的山体滑坡预测预警功能做数据准备。抗差自适应Kalman滤波算法的数据融合效果主要通过某一期的数据融合结果进行展示。 抗差自适应 Kalman滤波前后的数据对比如图10所示。图10中,蓝色实线为经抗差自适应Kalman滤波之后的滑坡监测点的形变量,红色点代表RTK定位的形变监测数据,绿色点代表土工带传感器的形变监测数据,黑色实线表示模拟设置的形变真值。调整无人机摄影测量的形变加速度信息,使之与土工带数据和RTK数据相匹配,可以看出滤波融合效果良好,在真值附近收敛,本次数据融合效果展示中无人机近景摄影测量的形变加速度a=0.0015(mm·d-2)。 图10 抗差自适应Kalman滤波前后数据对比 从图10可以发现,滤波收敛并稳定之后数据的最大值为5.984mm,最小值为5.570mm,与最初设置的真值5.8mm之间的误差不超过0.23mm,满足mm级监测精度要求。需要说明的是,由于所选取的用于展示抗差自适应Kalman滤波效果的这一期数据具有普适性,其监测精度即可反映普遍数据经抗差自适应Kalman滤波之后的监测精度,满足本文数据处理精度要求,为之后的山体滑坡预测预警算法提供了精确的数据支撑。 灰色预测理论形变预测结果与原模拟数据对比如图11所示。对比结果显示警戒级别数据经过Kalman滤波融合并经过灰色预测理论得到的警戒数据预测形变量曲线与警戒级别数据的形变量曲线基本重合,说明灰色预测理论预测的形变量与模拟设置数据的形变量接近,预测效果良好。 图11 灰色预测理论的形变预测效果图 灰色预测理论预测等级与原数据等级对比如表7所示。对比结果显示由灰色预测理论形变预测结果得到的预警等级与模拟设置数据的预警等级基本符合,仅在第4期数据上存在些许偏差,滑坡监测算法具备有效的滑坡预测预警功能。 表7 灰色预测理论预测等级与原数据等级对比 警报级别数据实验结果如表8所示,均值方差比C1为0.0296,明显小于0.35,即均值方差比精度等级为优;小概率误差P1为1,明显大于0.95,即小概率误差精度等级为优,所以该灰色预测模型的精度等级为优,形变预测结果精确。经过抗差自适应Kalman滤波的监测点的精确形变数据通过灰色预测理论预测之后得到的多期数据dL_Kalman_Grey_predict呈现上升趋势,即每隔2d滑坡监测点的形变量越来越大,预计第12期(8d后)采集到的形变量能达到0.43714m;形变速度呈现明显上升趋势,即滑坡监测点做加速形变,预计第12期(8天后)的形变速率能达到0.22388m/d;蠕变切线角angle呈现上升趋势,预计第12期(8天后)能够达到88.53°;预警等级warning_results也呈现上升趋势,第8期(最近数据采集时刻)的预警等级为3级,预计第9期的预警等级为3级,第10、11、12期(未来8天)的预警等级为4级,即为警报等级,未来一周内有非常大的概率出现山体滑坡灾害。 表8 警报级别数据实验结果 为进一步说明抗差自适应Kalman滤波算法对预测结果的影响,本文对未经过抗差自适应Kalman滤波融合的RTK形变监测数据单独通过灰色预测理论模型进行形变预测和预警等级分析,将预测预警结果与模拟设置数据的形变量和预警结果进行对比,同时与前文所述的经过抗差自适应Kalman滤波融合之后的滑坡预测预警效果进行对比分析。如图12所示,未经过抗差自适应Kalman滤波融合的RTK形变监测数据单独通过灰色预测理论进行形变预测得到的结果与模拟设置数据的偏差较大,形变预测效果变差。如表9所示,未经过抗差自适应Kalman滤波融合的RTK形变监测数据单独通过灰色预测理论和蠕变切线角判据得到的预警等级与模拟设置数据的预警等级存在的偏差明显增大,预警错误率增加,监测算法的预警效果变差。由表7和表9可知,使用抗差自适应Kalman滤波融合之后的数据,进行形变预测和预警分析的效果明显优于使用单一形变监测数据进行预测预警分析。可见抗差自适应Kalman滤波融合得到精确的形变监测数据,对于形变预测和预警分析是非常重要的。 图12 灰色预测理论的形变预测效果图(未经Kalman滤波融合) 表9 灰色预测理论预测等级与原数据等级对比(未经Kalman滤波融合) 由上述分析可知,本文设计了一种基于抗差自适应Kalman滤波和灰色预测理论的山体滑坡监测技术。该技术通过多种监测方式对易发生滑坡的监测区域进行形变监测,通过抗差自适应Kalman滤波技术对包括RTK定位数据、无人机摄影测量数据、土工带传感器数据在内的多源数据进行数据融合,最后通过灰色预测理论实现对监测区域滑坡形变程度和危险等级的预测。 与以往研究工作相比,本文所设计的滑坡监测技术的价值主要体现在以下几个方面: 1)本文所设计的滑坡监测技术具有很强的实时性。RTK定位技术、土工带传感器的使用,使得山体滑坡监测功能受天气状况和植被覆盖等因素的影响大幅减弱,能够及时发现和准确预测到可能发生的滑坡灾害,有效预防财产损失和人员伤亡。 2)本文所设计的滑坡监测技术自动化程度高。场外的设备一经布设,不需人工定期到现场进行勘探。场外的设备故障能够及时反馈到云端监测平台,只需有针对性地进行修复即可。与此同时,少量故障设备回传的错误信息也能通过算法滤波自行消化,对预测结果造成的影响很小。 3)本文所设计的滑坡监测技术的监测精度高。由上述仿真分析可知,由于土工带传感器形变监测、RTK静态形变监测和无人机摄影测量形变监测的精度均能达到mm级,外加抗差自适应Kalman滤波融合处理,该技术对于监测点处的形变监测精度可达mm级。 4)本文所设计的滑坡监测技术的设备成本低。土工带传感器辅助RTK形变监测和无人机摄影测量形变监测,大大降低监测成本,为大范围的山体滑坡监测提供了可行性。 本文目前尚存在一些不足之处,主要体现在受疫情影响和时间限制等多方面因素制约,缺乏实测数据进行实验验证,算法的分析仍停留在仿真层面,该问题待采得实测数据后即可解决。此外,本文所设计的滑坡监测技术尚未考虑地理水文、人类活动等相关因素,后续工作计划引入随机森林模型对影响滑坡的诸多因素进行分析。2 灰色预测理论
2.1 灰色预测模型(GM模型)
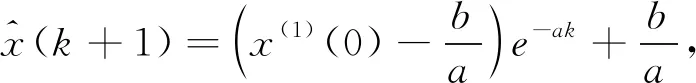

2.2 精度检验
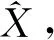
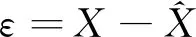
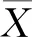

3 蠕变切线角判据


4 实验测试
4.1 滑坡监测系统

4.2 滑坡监测模型
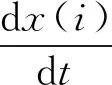

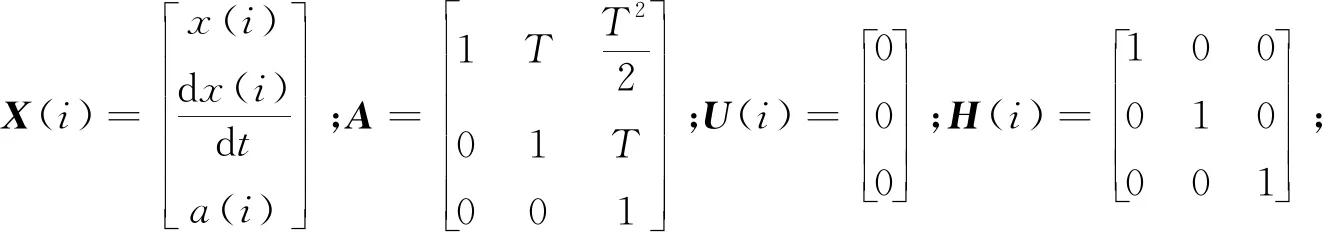
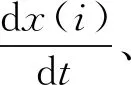

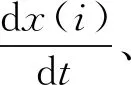
4.3 数据采集





5 结果分析
5.1 实验数据模拟设置


5.2 抗差自适应Kalman滤波融合结果

5.3 基于灰色预测理论和蠕变切线角判据的预测结果

5.4 抗差自适应Kalman滤波算法对预测预警的影响


6 总结
