基于总体性能最优的总体与动力联合优化

苏万兴，戴 林，张 赋，于建一

基于总体性能最优的总体与动力联合优化

苏万兴1，戴 林1，张 赋2，于建一1

（1. 北京机电工程总体设计部，北京，100854；2. 内蒙动力机械研究所，呼和浩特，010010）

为提升固体运载火箭总体性能，一方面不断提高发动机比冲与质量比等性能参数，另外，总体与发动机一体化联合优化也是切实有效的技术途径。以典型的固体运载火箭为例，探索了总体与发动机一体联合优化方向，对一级发动机与高空发动机开展了多途径优化，使火箭运载能力得到显著提升。

总体优化；固体发动机；联合优化

0 引 言

随着航天技术的发展，需要固体运载火箭具备更高运载能力和更轻的起飞重量。单纯依靠提升固体火箭发动机性能指标已难以满足上述要求，因此，固体运载火箭总体设计中越来越注重总体与发动机一体化设计[1,2]。通过联合优化设计，确定发动机的性能指标，以求挖掘系统潜力、从而提高火箭的综合性能。特别是对于多级固体火箭，发动机的内弹道形式、喷管扩张比、燃烧室压力等均是系统优化的核心要素；此外，通过合理优化动力系统的指标体系，使得运载火箭系统最优也是优化的重要方向之一[3]。

本文以典型的三级固体运载火箭为例，从运载能力最优的角度出发，开展总体与发动机一体化联合优化工作探索，对一级发动机的扩张比、内弹道形式进行了优化；对二、三级发动机的工作压强、扩张比等参数进行联合优化，提出了更加合理的比冲与质量比指标需求，结果表明可以实现运载能力的有效提升。

1 一级发动机扩张比优化

可见，扩张比是影响发动机比冲的重要因素，在低空下，喷管能量发挥最佳需要缩小扩张比，在高空下，喷管能量发挥最佳需要增加扩张比。

对一级发动机进行分析，图1给出了在海平面与海拔30 km高度条件下工作，不同工作压强、扩张比与比冲的关系曲线。

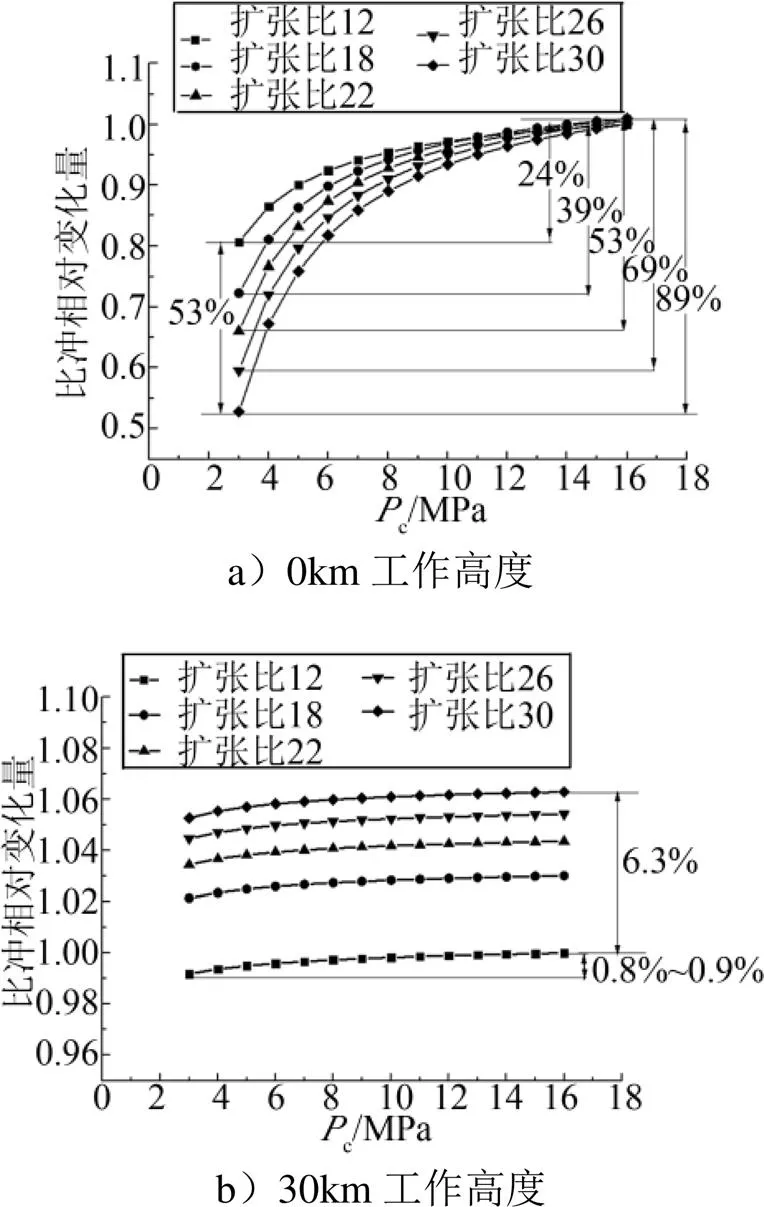
图1 不同工作压强与扩张比对比冲的影响

由图1可知，在海平面，影响发动机比冲的主要因素是工作压强与扩张比，在低工作压强下（以3 MPa为例），扩张比12与30相比较，比冲相差53%；在高工作压强下（以16 MPa为例），扩张比12与30相比较，比冲基本相当；在同一扩张比下（以扩张比18为例），随着工作压强的增加，比冲相应地提高，当压强由3 MPa提高至16 MPa时，比冲提升约39%。

在高空，影响发动机比冲的主要因素是扩张比，以工作压强16 MPa，扩张比为12与30为例比较，比冲相差6.3%。发动机高空工作时，工作压强对比冲的贡献较小，以扩张比12，工作压强3 MPa与16 MPa为例比较，比冲仅差0.8%～0.9%。

一级发动机工作过程经历的高度空间范围大，膨胀比随高度动态变化。根据上述分析，工作压强与扩张比对发动机比冲有较大的影响，一级发动机的设计应根据飞行弹道进行优化，按照飞行过程中能量发挥最优原则来设计喷管扩张比，从而实现火箭飞行过程总冲最佳，使运载能力提升。

对于三级固体运载火箭，结合飞行外弹道特点，对一级发动机的扩张比进行了多方案比较，表1给出了一级发动机不同初始扩张比下对运载能力的影响。

表1 初始扩张比对运载能力的影响

Tab.1 The Influence of Initial Nozzle Expansion Ratio on Launching Capability

设计高度/km初始扩张比总冲增幅运载能力增幅 000 4+8～1.0%～1.7% 5+12～1.2%～2.0% 6+15～1.3%～2.2% 7+16～1.3%～2%

以6 km高度最佳膨胀为例，发动机飞行过程总冲可增加1.3%，运载能力增加约2.2%。此外，扩张比的增大会导致喷管结构质量增加，总体设计中需综合考虑比冲对运载能力的效益、喷管增大后惰性质量对运载能力的损失以及喷管出口的约束条件，从而设计合理的初始扩张比。

2 一级发动机内外弹道一体化优化

考虑火箭一级飞行段的飞行过程和弹道约束，一级发动机推力大小、工作时间等参数对运载能力有显著影响。理论表明[5,6]，推重比对固体火箭的运载能力影响显著。在火箭一级飞行过程中，尤其是初始段，弹道倾角大，一级发动机若具备大的推重比，可减小重力损失，提升运载能力。假设火箭垂直向飞行（弹道倾角90°，全程飞行攻角为0，飞行高度单调变化），忽略地球自转和气动阻力的影响，重力、推力也近似按照常值考虑，研究发动机工作期间推力大小变化对机械能的贡献。

（4）

可见，在起飞质量和发动机总冲一定的情况下，发动机流量越大，对应的推力和推重比也越大，推力做功效率越高，火箭在一级发动机关机点获得的机械能也越大。

以固体运载火箭为例，推重比对推力效率的影响见图2。在发动机总冲不变的前提下，推重比从1.4提高到1.6，垂直向上飞行获得的机械能可以增加约13%，表明发动机推重比对火箭运载能力有显著影响。

图2 推重比对推力效率的影响

大推重比有利于提高运载能力，因此希望发动机具有大推力，但是，在发动机总冲不变的条件下，增大推力会导致工作时间缩短，快速助推火箭将承受更加严酷的热环境和更高的动压，将使一、二级级间分离动压增大，难以满足分离约束条件，这是一级发动机总体设计中存在的主要矛盾之一，见图3。根据固体运载火箭飞行弹道特点，总体与动力开展了内外弹道联合优化设计，对一级发动机进行了能量优化分配，在低空段采用大推力形式，以较大的推重比提升运载能力；在高空段采用小推力长时间飞行，弹道倾角已经较小，重力损失影响减弱。

图3 一级发动机工作时间与级间分离动压（无量纲）关系

通过上述优化，三级固体运载火箭运载能力提升3.5%，级间分离动压降低约15%，较好满足了提升运载能力与降低分离动压的需求，可以取得显著效果。

3 高空发动机工作压强优化

对于高空发动机，要获得高比冲，需要有大的扩张比，但会导致喷管质量增大，质量比降低。通过增加发动机工作压强，可以缩小喷管喉径，减轻喷管质量，但又会导致壳体结构质量增加。因此，高空发动机工作压强是平衡比冲与质量比关系的主要参数[7]，需以运载能力最优为目标，对发动机进行优化设计，寻找比冲与质量比之间的平衡点。

此外，各级发动机质量比、比冲对火箭运载能力的贡献有所不同，两者之间也需要进行综合优化选取，因此，有必要进行总体与发动机的一体化设计。

美国固体导弹的设计比较注重总体与发动机一体化设计，其设计思路是以获得全弹综合性能指标最优为目标，而不是单独追求发动机性能指标最优[8]。例如民兵-3导弹二、三级发动机平均扩张比分别为24.8、23.6，与传统高空发动机单纯追求大扩张比相悖，但其全弹的综合性能优越，体现了总体与发动机一体化设计的必要性。

3.1 二级发动机优化

以指标要求（质量比、比冲sp）下的运载能力为基准，对二级发动机工作压强进行了优化，优化目标为运载能力最佳。根据比冲与结构质量对运载能力的偏导数关系，计算分析了不同工作压强下质量比、比冲以及运载能力增量情况（见表2）。表2结果表明，方案3为最优方案，优化后运载能力增加7.5 kg。

表2 二级发动机不同方案对比

Tab.2 Comparison of Second Stage SRM Schemes

方案平均工作压强/MPa质量比比冲/s运载能力增益*/kg 1P-1.5μ+0.004Isp-0.74.5 2P-0.3μ+0.0035Isp6.4 3Pμ+0.003Isp+0.57.5 4P +0.5μ-0.001Isp+0.60.5 5P+1.3μ-0.003Isp+0.8-2.3

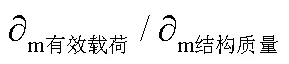
3.2 三级发动机优化

同样，以指标要求（质量比、比冲sp）下的运载能力为基准，基于三级发动机比冲和结构质量对运载能力的偏导数关系，对三级发动机的工作压强进行优化（见表3）。表3结果表明，方案3为最优方案，优化后运载能力增加6.2 kg。

表3 三级发动机不同方案对比

Tab.3 Comparison of Third Stage SRM Schemes

方案平均工作压强/MPa质量比比冲/s运载能力增益/kg 1P-1.2μ+0.0018Isp-0.463.9 2P-0.7μ+0.0009Isp+0.24.1 3Pμ+0.0003Isp+1.036.2 4P +0.4μ+0.0015Isp+1.512.3 5P +0.8μ+0.0025Isp+1.991.3

基于上述分析，总体与动力一体化联合优化是提升运载能力的有效途径之一，在固体火箭总体方案设计中，应结合火箭实际特点，根据比冲、结构质量对运载能力的偏导数关系，对高空发动机进行挖潜优化，合理设计比冲与质量比之间平衡点，从而优选能够更好满足总体要求的发动机方案。

4 结 论

a）对于固体运载火箭而言，一级发动机飞行空域跨度较大，扩张比的设计需根据飞行过程进行优化设计，按特定高度最佳膨胀设计，从而获取最佳的飞行总冲，有效提升了固体火箭的运载能力。

b）根据飞行弹道的特点与需求，通过内外弹道联合优化，合理地设计内弹道形式，进行发动机冲量的合理分配，较好满足了提升运载能力与降低级间分离动压的需求，此外，还降低了发动机的设计难度、提高了发动机工作可靠性，获得了总体与发动机共赢的效果。

c）高空发动机的设计应以运载能力最优为设计原则，按照比冲、结构质量对运载能力的偏导数关系对发动机方案进行优化，从而获得更为合理的发动机方案。

d）在总体方案设计中，应加强总体与动力的一体化联合优化，不单一地追求发动机单项指标最优，根据总体外弹道特点、基于固体运载火箭性能最优为目标，通过联合优化，合理设计发动机内弹道形式、优化能量分配、优化和完善动力系统指标体系，从而使火箭的综合性能达到最优。

[1] 徐玮, 孙丕忠, 夏智勋. 助推-滑翔导弹总体一体化优化设计[J]. 固体火箭技术, 2008, 31(4): 317-320.

Xu Wei, Sun Pizhong, Xia Zhixun. Integration design and optimization for boost-glider missile[J]. Journal of Solid Rocket Technology, 2008, 31(4): 317-320.

[2] 杨军, 陈汝训, 赵锡良. 战术火箭/固体火箭发动机一体化优化设计[J].宇航学报, 1999, 20(1): 21-27.

Yang Jun, Chen Ruxun, Zhao Xiliang. Integral optimization design for tactical rocket and it's srm by utilizing the synthesis of internal ballistic and trajectory[J]. Journal of Astronautics, 1999, 20(1): 21-27.

[3] 陈铁彪, 王洪波, 龚旻. 基于伪谱法的多级火箭总体/弹道一体化优化方法[J]. 导弹与航天运载技术, 2019, 5(3): 8-11.

Chen Tiebiao, Wang Hongbo, Gong Min. Study on the integrated optimization technique of multi-stage launch vehicle Based on Pseudo-spectral Method[J]. Missiles and Space Vehicles, 2019, 5(3): 8-11.

[4] 董师颜, 张兆良. 固体火箭发动机原理[M]. 北京: 北京理工大学出版社, 1996.

Dong Shiyan, Zhang Zhaoliang. Principle of solid rocket motor[M]. Beijing: Beijing Institute of Technology Press, 1996.

[5] 刘新建. 导弹总体设计导论[M]. 北京: 国防工业出版社, 2017 .

Liu Xinjian. Introduction to missile overall design[M]. Beijing: National Defence Industry Press, 2017.

[6] 蒋明明, 袁庆航, 赵长见. 助推-滑翔式导弹总体参数设计方法初探[J]. 导弹与航天运载技术, 2016, 2(4): 5-21.

Jiang Mingming, Yuan Qinghang, Zhao Changjian. Preliminary investigation of parameter design method for boost-glide missile[J]. Missiles and Space Vehicles, 2016, 2(4): 5-21.

[7] 万少文, 赵志敏, 胡昌宇. 工作压强对战术固体火箭发动机比冲的影响

分析[J]. 固体火箭技术, 2003, 26(2): 4-7.

Wan Shaowen, Zhao Zhimin, Hu Changyu. Effect of operation pressure on the specific impulse of tactical missile solid motors[J]. Journal of Solid Rocket Technology, 2003, 26(2): 4-7.

[8] 张宗美. 民兵洲际弹道导弹[M]. 北京: 宇航出版社, 1997.

Zhang Zongmei. Minuteman intercontinental ballistic missiles[M]. Beijing: Aerospace Publishing House, 1997.

Joint Optimization for Solid Rocket Motor based on the System Optimal Strategy

Su Wan-xing1, Dai Lin1, Zhang Fu2, Yu Jian-yi1

(1. Beijing System Design Institute of Electro-mechanic Engineering, Beijing, 100854;2. Inner Mongolia Power Machinery Research Institute, Hohhot, 010010)

In order to improve the performance of solid launch vehicles, on one hand, the specific impulse and mass ratio of solid rocket motor should be enhanced, on the other hand, joint optimization for solid rocket motor based on the system optimal strategy is a practical and effective method. Take the typical solid launch vehicle for example, the joint optimization for solid rocket motor is studied. The performance of solid launch vehicle is greatly improved via joint optimization for both the first stage and high altitude solid rocket motors.

system optimal strategy ; solid rocket motor; joint optimization

2097-1974(2023)01-0007-04

10.7654/j.issn.2097-1974.20230102

V421.1

A

2022-10-08；

2022-11-01

苏万兴（1987-），男，博士，高级工程师，主要研究方向为飞行器总体设计。

戴 林（1985-），男，高级工程师，主要研究方向为制导与姿态控制。

张 赋（1986-），男，博士，高级工程师，主要研究方向为固体发动机设计。

于建一（1990-），男，博士，高级工程师，主要研究方向为结构与防热设计。