非对称Colonel Blotto博弈模型下的多信道功率分配抗干扰*
2023-03-09王世练陆锐敏骆俊杉
魏 鹏,王世练,陆锐敏,骆俊杉
(1. 国防科技大学 第六十三研究所, 江苏 南京 210007; 2. 国防科技大学 电子科学学院, 湖南 长沙 410073)
随着人工智能的飞速发展和软件无线电能力的不断提升,无线通信面临的智能化干扰威胁越来越严重。传统以宽带高速跳频和非协调跳频等扩频技术为主的抗干扰通信技术,每次只使用一个信道,频谱利用率低[1],且难以有效应对跟踪干扰和超出扩频增益的宽带干扰。如何在干扰条件下通过功率控制提升通信系统效能,一直是通信领域关注的重要方面,特别是在通信对抗双方日益智能化的条件下,通过博弈论来解决双方的最优功率分配问题得到越来越多的研究。根据通信对抗双方可用信道数,基于功率分配的对抗博弈可分为单信道模型和多信道模型。对通信方而言,可用信道数定义为一次通信过程中用户不受其他用户干扰而独占的频分信道数,可以由连续或不连续的多个频段组成;对干扰方而言,可用信道数定义为一次干扰过程中可不受限制自由干扰的信道数,通常与通信方可用信道一致。
单信道模型的功率分配通常为对抗双方引入功率开销代价,以最大化、最小化通信容量或信噪比为目标,将对抗双方建模为非合作博弈[2-5]、二人零和博弈[6]、Stackelberg博弈[7-8]等,然后求解博弈的纳什均衡[2-5,9]或Stackelberg均衡[8]。在存在用户间互干扰的情况下,也可能进一步追求帕累托最优[10]。对模型中存在的某些未知参数,通常使用Q-Learning[6]等强化学习算法获取。其中,文献[2]将无线网络中的功率控制问题建模为一个广义非合作博弈,联合优化无线网络中的能效和延时,分别提出了分布式和集中式功率控制算法,并采用最大块改进方法解决了非凸集中功率控制问题,保证了功率控制算法收敛到较好的候选解,且复杂度适中。文献[3]将分布式无线传感器网络中的传感器功率分配建模为非合作博弈,提出了一种非协作功率控制算法,使节点能够快速收敛到使网络性能稳定的纳什均衡点。文献[4]将认知无线电中的功率控制问题建模为非合作功率控制博弈,提出了一种自适应非合作功率控制算法,证明了该算法存在唯一纳什均衡,并且能够降低功耗,克服远近距离效应。文献[5]考虑干扰温度,将认知传感器网络中的节能功率分配问题描述为非合作耦合约束博弈,设计了基于效率的集中式和分布式功率分配算法并得到纳什均衡,具有良好的能量效率、收敛速度和公平性。文献[6]将认知无线电与干扰机之间的功率分配交互建模为二人零和博弈,提出了一种基于Q-Learning的多通道功率分配算法,该算法在固定干扰策略下,学习解与平坦衰落信道下常见的显式注水解相等,选择性信道下略有不同;在智能干扰策略下,学习到的策略几乎等于完全信息博弈的均衡策略。文献[7]将DoS攻击下无线通信网络的最优功率调度问题建模为不完全信息Stackelberg博弈,将自适应惩罚函数方法和微分进化算法相结合,处理相应的非线性和非凸优化问题。文献[8]将智能干扰机存在下的单通道功率控制抗干扰建模为Stackelberg博弈,给出了Stackelberg均衡策略的闭式表达式,证明了Stackelberg均衡的存在性和唯一性。文献[9]分别采用非合作纯策略博弈和混合策略博弈对蜂窝网络中设备间功率控制问题进行了研究和探讨,针对每一种博弈,导出了功率受限的纳什均衡封闭表达式,并研究了纳什均衡的存在性和唯一性。文献[10]研究了多用户中继网络单流传输(single-stream transmission)中的功率分配问题,采用可行点跟踪逐次凸逼近和多目标分析方法来计算一组近似帕累托最优的信噪比,仿真结果证明提出的算法优于比较方案。
多信道模型的功率分配根据优化目标不同,求解方法差异很大。当优化目标为通信容量时,文献[8]引入了功率开销代价,证明了Stackelberg均衡的存在性,设计了计算干扰机的最佳响应策略和用户近似最优策略的算法。文献[11]证明了在白噪声信道下,通信对抗双方的纳什均衡策略是双方均在所有可用信道上平均分配功率,而在频率选择性衰落信道下,通信对抗双方的纳什均衡策略可用迭代注水算法求解。文献[12]以信干噪比(signal to interference plus noise ratio,SINR)作为优化目标,将中继网络多个合法中继节点与智能干扰器之间的功率对抗过程建模为一个两层Stackelberg博弈,分别研究干扰者与合法节点之间的敌对关系及合法节点之间的协作关系,并求得了Stackelberg均衡。这种以通信容量或SINR为优化目标的多信道功率分配方法虽然有完备的理论支撑,但在实际通信系统中并不适用。因为实际通信系统均以特定的速率传输信息,当接收信号不低于解调门限时,一包数据接收成功;反之,该包数据接收失败。而当SINR达到解调门限后,更大的通信功率并不能进一步提高通信容量。因此,通信对抗双方最大化或最小化的目标应为传输成功的信道数。这种以特定通信速率下传输成功的信道数为优化目标的多信道功率分配方法通常建模为Colonel Blotto博弈[13-15]。其中,文献[13]研究了认知无线电网络中的次级用户与攻击者之间的博弈,在次级用户与攻击者均可以访问多个信道场景下,将次级用户与攻击者之间的功率分配问题建模为Colonel Blotto博弈,通过构造一种匹配期望边际分布且满足总功率约束的联合分布,最终获得了纳什均衡策略,以最小化通信方最坏情况下的损失,但如何找到由联合概率分布确定的纳什均衡策略仍然是一个难题。文献[14]提出了一种基于Blotto博弈的多维拍卖子载波分配方案,主要用以解决兼顾效率和公平的多载波分配问题,其效用函数是加权的香农容量公式。文献[15]将认知无线电中二级用户与干扰者之间的多信道功率分配问题建模为双人Blotto博弈,并采用迭代纳什议价解对模型求解,其效用函数是信干噪比的偏置加权,等效于以通信容量为优化目标。
综上所述,单信道功率博弈问题和以通信容量为优化目标的多信道功率博弈问题已经得到了很好的解决,而以特定速率下传输成功的信道数为优化目标的多信道功率分配博弈仍有待深入研究。此外,随着通信对抗双方信号处理能力的提升,同时处理多个信道将变得越来越容易。通信方通过在多个信道上以某种优化策略分配通信功率,可作为一种智能抗干扰手段,在智能干扰条件下最大化通信方收益。
本文以文献[13]的多信道功率分配模型为基础,结合实际系统中数字化功率控制特点,针对非对称Colonel Blotto博弈模型以及该模型下的多信道功率分配抗干扰问题,首先建立了一种非对称Colonel Blotto博弈模型,将Colonel Blotto博弈应用范围推广至战场对博弈双方不公平的场景;然后基于所提模型,针对通信对抗双方数字化功率控制场景,提出了通信对抗双方不同功率约束下的最优混合策略及纳什均衡相关定理,并通过求解等效单信道最优功率分配策略进行了证明;最后基于等效单信道最优功率分布,设计了一种线性规划方法求解多信道混合功率分配矩阵,并针对该方法难以适应较多信道数和较广功率分布范围的不足,提出了一种多重扫描直接列元素交换算法,可快速构建多信道混合功率分配矩阵,并且具有更广的适用范围。
1 Colonel Blotto博弈及多信道功率分配
1.1 Colonel Blotto博弈
Colonel Blotto博弈是一种二人零和博弈,又称Divide Dollar博弈,博弈双方分别记为B(Blotto)和E(Enemy)。博弈的规则为B和E在K个独立的战场上同时分配各自有限的兵力,但均不知道对手某一次的具体分配策略。若一方在某战场上分配了比对方更多的兵力,则在该战场上获胜,收益记为1。博弈的收益为赢得战场的总数,赢得大部分战场的一方最终获胜[16]。

(1)
sign(z)表示取z的符号,即
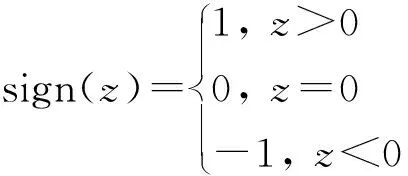
(2)
对该博弈问题的大量深入研究[16-20]表明,该博弈不存在纯策略纳什均衡,因此重点研究在各种约束下的混合策略纳什均衡。其中,与本文研究最相关的是文献[17]所做的工作。该文献首先将Colonel Blotto博弈等价为General Lotto博弈,即在单个战场上满足平均兵力约束的博弈,然后将其结果推广至K个战场完成Colonel Blotto博弈。遗憾的是,虽然General Lotto博弈得到完美的解决,但将其结果推广至K个战场时,并不总是存在可行解,因此并没有完全解决Colonel Blotto博弈问题。
受该文献思路的启发,本文提出了一种非对称Colonel Blotto博弈,用于解决数字化功率控制条件下通信对抗双方的多信道功率分配问题。不同于传统Colonel Blotto博弈中每个战场对博弈双方公平的假设,多信道功率分配博弈中,干扰方在每个信道上都有噪声进一步加强其干扰效果,这可等效为Colonel Blotto博弈中每个战场对博弈对抗双方不公平,也即一方占有主场优势,能够以相同或更少的兵力获胜。
1.2 多信道功率分配及非对称Colonel Blotto博弈模型
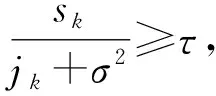
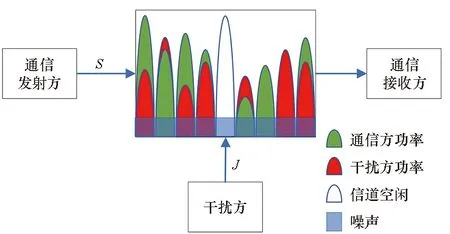
图1 多信道功率分配示意图Fig.1 Diagram of multi-channel power allocation
需要说明的是,即使通信方具有更小的功率分配粒度,也不能进一步增加其收益。因为当SINR等于门限τ时,通信成功,高于门限的功率不能带来额外的收益;同理,当S不能够被τd整除时,剩余不足τd的功率增加到任一信道上均不能改变对应信道上的收益。因而假定通信方总功率控制精度为τd,且总功率S能够被τd整除对通信方来说是最优的。此外,若干扰方能够进一步细化功率分配粒度d,使得通信方功率分配粒度达不到τd,则在某些干扰功率下,通信方无法使SINR等于门限τ,因此,通信方为正确接收数据,需付出比达到解调门限所需功率更大的功率代价,也即提升了干扰方收益。本文暂不考虑这种情况,均假定通信方具有较强的功率控制能力,使功率分配粒度达到τd。
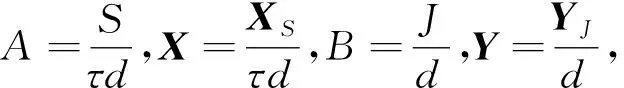
(3)
其中,gte(z)表示判断z是否大于等于0,即
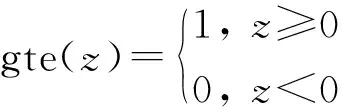
(4)
将式(1)~(4)给出的Colonel Blotto博弈模型进行对比,可见,因受白噪声影响,信道对通信对抗双方不再公平,即非对称。相比于Colonel Blotto博弈模型战场对博弈双方公平的假设,本文所提非对称Colonel Blotto博弈模型具有更广的适用范围,不仅适用于多信道功率分配,同样也可应用于非对称战场兵力分配。例如,当作战双方B和E中的某一方通过修筑防御工事或可更充分利用地形而占据主场优势时,战场对双方不再对称,占据主场优势的一方能以相同或更少的兵力获胜。
2 非对称Colonel Blotto博弈模型下的多信道功率分配策略
2.1 相关定义及定理
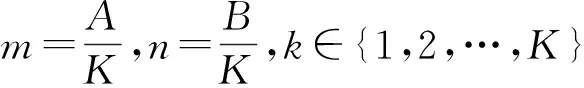
定义1通信方全信道功率均匀分布。若通信方同时有K个信道可用,第k信道上的功率分配服从u至2m-u之间的均匀分布,且任一纯策略i在K个信道上分配的功率满足总功率约束,即
则称之为通信方全信道功率均匀分布策略。 其中,u=「n0⎤为受功率分配粒度τd约束的大于等于归一化白噪声n0的最小整数,「·⎤表示上取整。
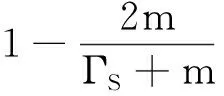
则称之为通信方以ΓS(ΓS>2m-u)为上限的部分信道功率均匀分布策略。 其中,O表示功率为0的集合。
定义3干扰方全信道功率均匀分布。 若干扰方可同时干扰K个信道,在第k个信道上分配的功率服从0至2n之间的均匀分布,且任一纯策略j在K个信道功率之和满足总功率约束,即
则称之为干扰方全信道功率均匀分布策略。
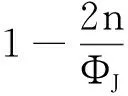
则称之为干扰方以ΦJ(ΦJ>2n)为上限的部分信道功率均匀分布。
假定通信对抗双方均能根据对方的混合策略分布,选择己方的最优功率分布策略,则根据上述定义,提出如下通信对抗双方多信道最优功率分配策略相关定理。
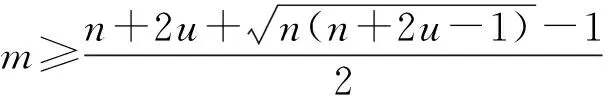
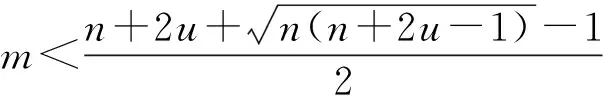
推论1干扰方的最优功率分配策略一定是以Φ(Φ>2n)为上限的部分信道功率分配策略。
对上述定理的证明利用了文献[17]的结论,即Colonel Blotto博弈具有与General Lotto博弈相同的值(value),然后取消K个战场的限制将其等效为单个战场的General Lotto博弈。结合本文多信道功率分配模型,可等效为通信方和干扰方在单个信道上满足平均功率约束的功率分配博弈,即任意第k信道服从的最优功率分布一致,期望收益均等于K信道Colonel Blotto博弈的期望收益。对该等效的合理性可直观理解为:既然在每个无差别信道上的功率分配都是最优的,则在所有信道上必然也是最优的。于是,从通信方角度出发,通信方收益可表示为:
RS(X,Y)=RS(xk,yk)
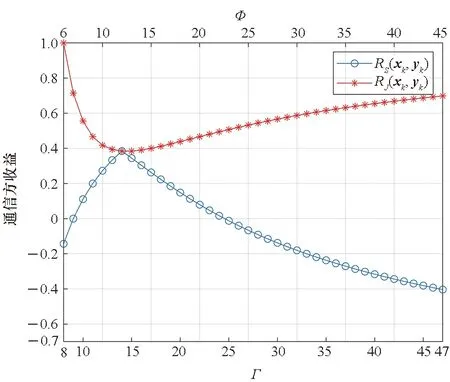
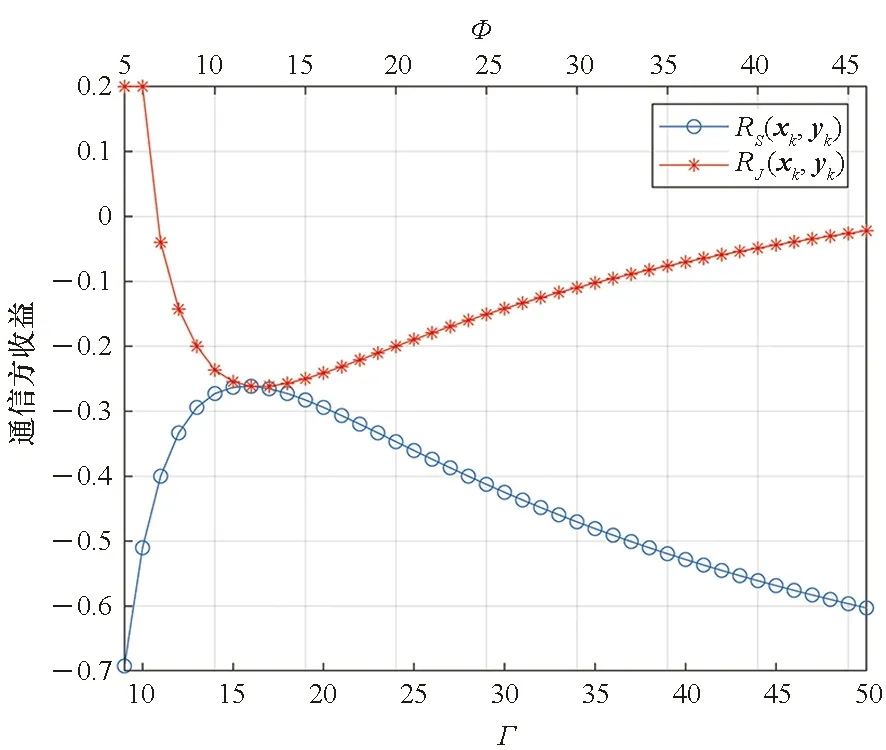
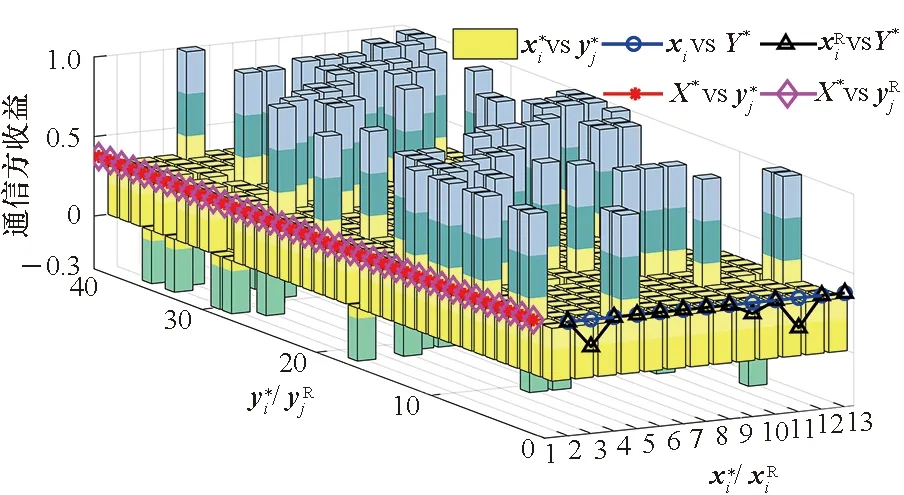
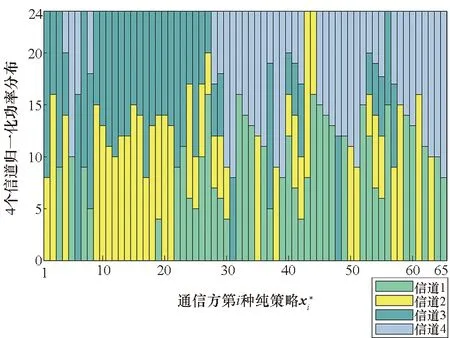
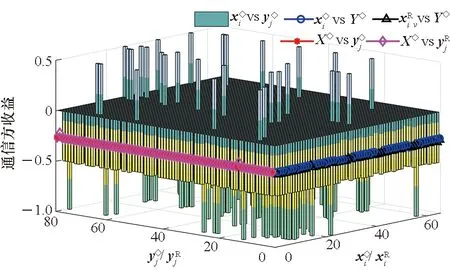
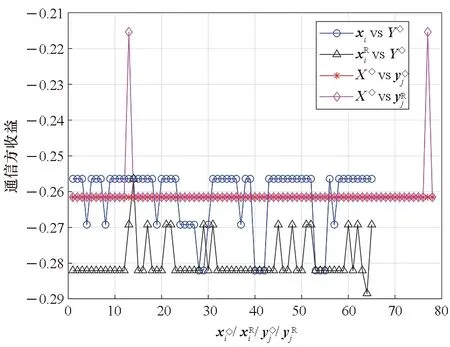
=P(xk≥yk+u)-P(xk (5) (6) 设通信方在第k个信道上分配的最大功率值为Γ。当Γ≤2m-u时,满足平均功率约束的通信方全信道功率均匀分配策略为xk=[2m-Γ,2m-Γ+1,…,Γ]。根据式(5),最坏情况下(因为干扰方可根据通信方混合策略分布选择使通信方收益最小的功率分配策略),通信方在第k个信道上的收益为: (7) (8) 综合式(7)和式(8)可得通信方收益随Γ变化的函数为: (9) 式中,当Γ≤2m-u时,通信方收益RS(xk,yk)随Γ增加而单调递增,因此通信方应使Γ=2m-u,即通信方全信道功率分配策略是通信方最优功率分配策略;当Γ>2m-u时,RS(xk,yk)对Γ求导可得: (10) 此结果证明了定理1和定理2中通信方的最优功率分配策略。 (11) (12) 式中,通信方可通过调整自身功率分配使ΓS≤Φ+u,使得等号成立。 综合式(11)、式(12)可得 RJ(xk,yk) (13) 当Φ>2n时,RJ(xk,yk)对Φ求导可得: (14) 上述结果证明了定理1和定理2中干扰方最优功率分配策略,以及推论1。 图 2给出了分别与式(9)、式(13)对应的通信对抗双方的收益变化曲线,两个横轴Γ和Φ分别表示通信方、干扰方的最大功率分布值,对应式(9)、式(13)中的自变量。纵轴对应式(5)和式(6)给出的从通信方角度和干扰方角度得到的通信方收益RS(xk,yk)和RJ(xk,yk)。可见通信方在Γ=ΓS=2m-u=14处使收益取得了极大值0.384 6,干扰方在Φ=ΦJ=2m-2u=12和Φ=ΦJ=2m-2u+1=13处使通信方收益取得极小值0.384 6,也即通信方对抗双方达到了纳什均衡,且纳什均衡收益为0.384 6。 图2 通信方收益随通信方、干扰方功率分布变化曲线1Fig.2 Payoff curve 1 of the communication system with the power distribution 图3 通信方收益随通信方、干扰方功率分布变化曲线2Fig.3 Payoff curve 2 of the communication system with the power distribution 由图 2、图 3纳什均衡点对应的通信对抗双方的归一化功率分布,可方便地得到实际功率分布,而由纳什均衡收益和信道数K容易求出可成功通信的信道数Ksuc,如式(15)所示。 (15) 另外还有两点需要说明:首先,上述纳什均衡点及其收益都是在通信方与干扰方均匀分布其功率的条件下求得的。事实上,若某一方不服从均匀分布,而更加偏好某些策略,则其对手总可以找到针对性策略,使得通信收益高于或低于纳什均衡收益,后续的数值仿真结果也验证了这一点。其次,上述纳什均衡是基于完全信息条件推导的,即对抗双方均已知对方总功率、功率分配粒度、可用信道数及通信方正确接收一包数据所需的门限信干噪比。实际应用过程中,干扰方可通过前期侦察获得所需的通信方参数,通信方也可通过干扰认知学习到所需的干扰方参数。 上述通信对抗双方最优功率分配策略及纳什均衡的求解是通过将K个信道上的功率分配博弈等效到单个信道上满足平均功率约束的功率分布求得的,而将求得的单个信道上的功率分布推广到K个信道,构建满足总功率约束的K信道混合策略功率分配矩阵,仍然是一项困难的任务。本文首先提出一种线性规划求解方法,可以对信道数少、功率分布范围小的混合策略功率分配矩阵进行快速构建。但当信道数较多或功率分布范围较大时,则求解速度过慢,甚至得不到可行解。为此,提出了一种多重扫描直接列元素交换算法,可以快速构造功率分布范围较大的K信道混合策略功率分配矩阵。以通信方K信道混合策略功率分配矩阵的构建为例介绍两种方法。 (16) (17) 其中,Pk为L×L行置换矩阵,其元素为pk(i,j),k∈{1,2,…,K},Pk的每行每列只有一个元素为1,其余元素均为0,A为通信方归一化总功率。 则X中各列元素的调整可通过求解K个列置换矩阵Pk实现,而Pk的求解可转化为标准的线性规划模型,具体步骤如下: 步骤2:确定约束矩阵方程CV=b。 约束矩阵方程由式(17)中的3个等式约束转换得到,C矩阵共(2K+1)L行、KL2列,满足 (18) 步骤4:求解整数线性规划。 综合步骤1~3,该线性规划问题的标准表达式如下: (19) 任意满足式(19)约束的整数解均能使优化目标f达到其极小值KL,该解可通过MATLAB、LINGO等工具软件中的线性规划工具箱求得。 步骤5:构建K信道混合策略功率分配矩阵。求得未知向量V后将其等分为K个列向量,并分别转换回Pk,即 Pk=reshape([v(k-1)KL+1,v(k-1)KL+2,…,vkKL],K,L) 最后,再利用式(16)求得X*。 使用该线性规划方法构造K信道混合策略功率分配矩阵所求解的未知数为KL2个,当KL2较小时(KL2<1 000),使用MATLAB可快速求解;但当KL2较大时,求解该线性规划耗时急剧增加,甚至难以找到可行解。 针对线性规划方法的不足,提出了多重扫描直接列元素交换算法来构造混合策略功率分配矩阵,算法流程如图4所示。 图4 多重扫描直接列元素交换算法流程Fig.4 Flowchart of the Multi-scan direct column element exchange algorithm 算法1中,row(Fr)表示矩阵Fr的行数,length(chx_n)表示向量chx_n的元素个数,find(X(Fr,k)==X(Fr(i),k)-sum(X(Fr(i),:)-A))为在Fr中所有不满足功率约束的行的第k列寻找能够使第i行之和为A的元素,并记其集合为向量chx_n,chx_n(randi(length(chx_n)))为在向量chx_n中随机选择一个元素,exchange(X(i,k),X(j,k))表示将矩阵X中第i行k列的元素与第j行k列的元素互换位置,rem(i,length(Fr))表示i对向量Fr的长度求余。 算法1 多重扫描直接列元素交换算法Alg.1 Multi-scan direct column element exchange algorithm 算法1(续) 使用算法1,可根据单信道功率分布快速构建通信对抗双方的功率分配矩阵,对于本文用于数值试验的4信道、每信道78种分布的功率分布矩阵构造,多数情况下在20次循环内可完成,耗时仅需数秒。而用线性规划方法,运行1 h以上仍得不到可行解。 选择2组参数对所提定理进行仿真验证,2组参数分别对应定理1和定理2所提的2种功率分布,且与图2、图 3所用参数保持一致。 图5 第1组参数下通信方最优混合策略功率分配矩阵Fig.5 Optimal mixed strategy power allocation matrix of the communication system under the first set of parameters 图6 第2组参数下干扰方最优混合策略功率分配矩阵Fig.6 Optimal mixed strategy power allocation matrix of the jammer under the second set of parameters 图7 第1组参数下各种策略组合的通信方收益Fig.7 Payoff of the communication system with various strategies combinations under the first set of parameters 图8 第2组参数下通信方最优混合策略功率分配矩阵Fig.8 Optimal mixed strategy power allocation matrix of the communication system under the second set of parameters 图10 第2组参数下各种策略组合的通信方收益Fig.10 Payoff of the communication system with various strategies combinations under the second set of parameters 图11 第2组参数下通信方或干扰方纯策略与对方最优混合策略组合下的通信方收益Fig.11 Payoff of the communication system with the combinations of a pure strategy and the optimal mixed strategy of the opponent under the second set of parameters 本文提出一种非对称Colonel Blotto博弈并将其应用于通信对抗双方多信道功率分配博弈,推导出了不同功率约束下通信对抗双方的最优功率分配策略,并证明了混合策略均衡的存在性和唯一性。提出了基于多重扫描直接列元素交换算法,使得通信对抗双方可根据各自等效单信道最优功率分布构建多信道混合策略功率分配矩阵。最后仿真验证了所提理论的正确性及算法的有效性。不足之处在于,本文仅考虑了通信对抗双方总功率均能够被信道数整除的情况,且信道均为一致的白噪声信道。因此,进一步研究方向包括通信对抗双方总功率不能被信道数整除以及各信道状态不一致时的功率分配博弈。这些条件下,博弈模型的建立和求解将变得更加困难,因而拟采用对抗学习的方法来解决该问题。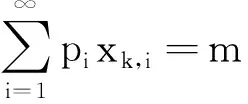
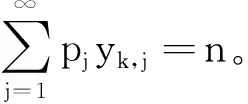
2.2 通信方最优策略证明
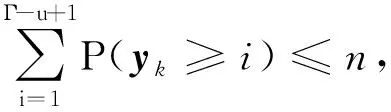
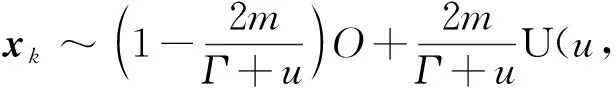
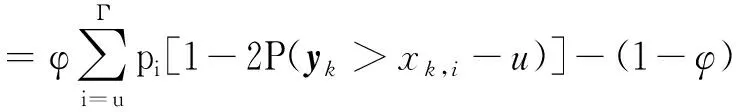
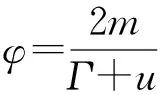
2.3 干扰方最优策略证明
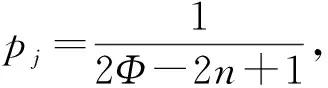
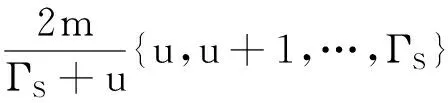
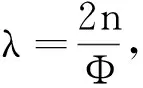
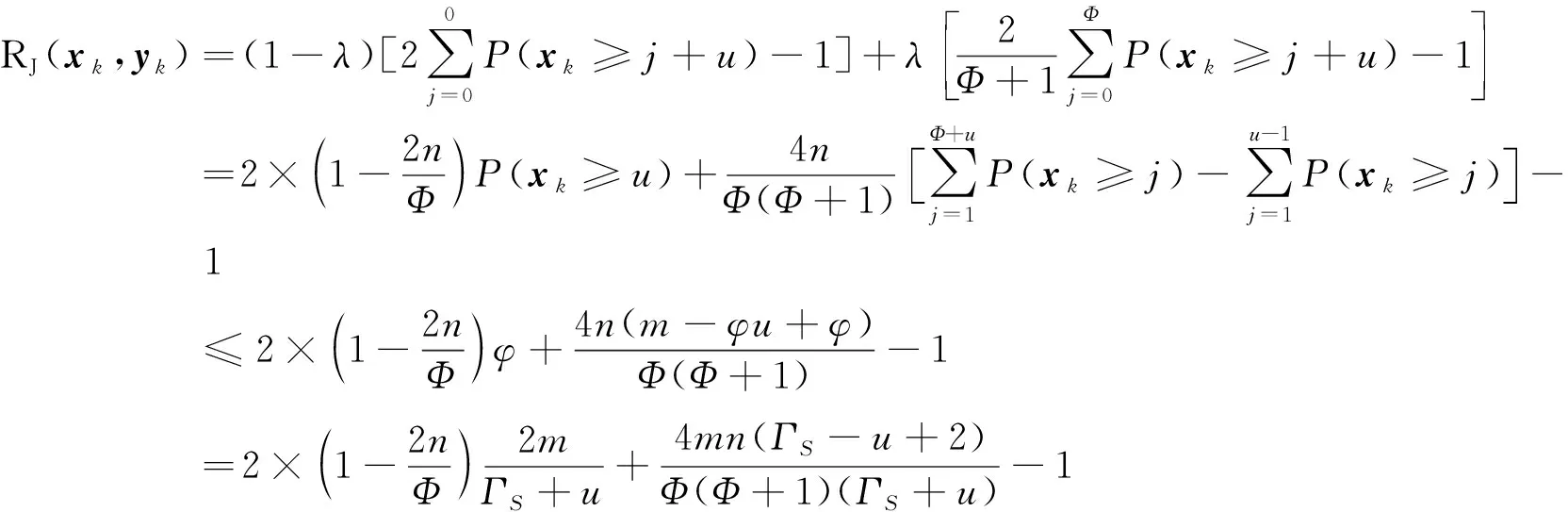
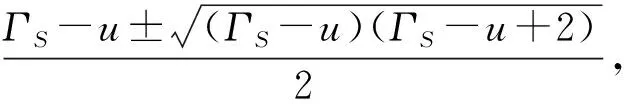
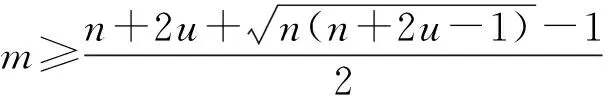
2.4 纳什均衡策略证明
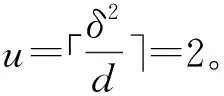
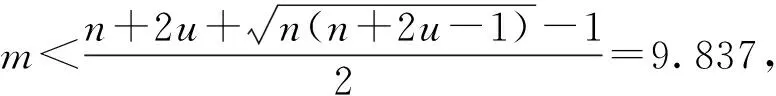
3 混合策略功率分配矩阵的构造
3.1 线性规划方法

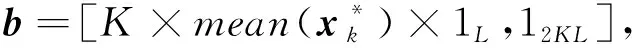
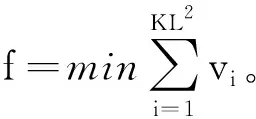
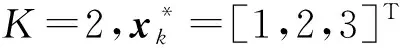

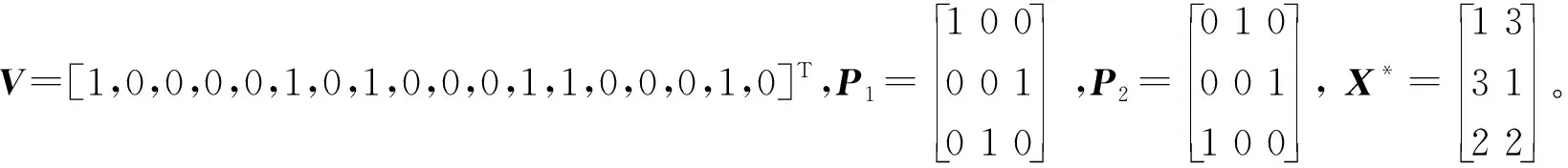
3.2 多重扫描直接列元素交换算法
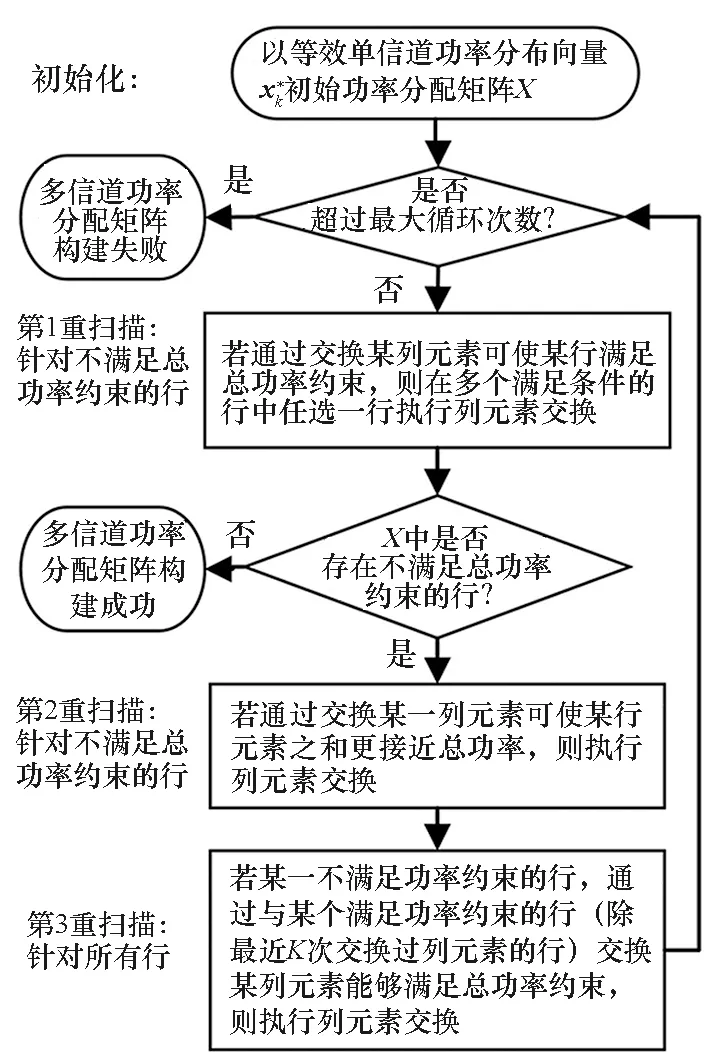
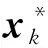


4 数值仿真验证
4.1 第1组参数仿真验证结果
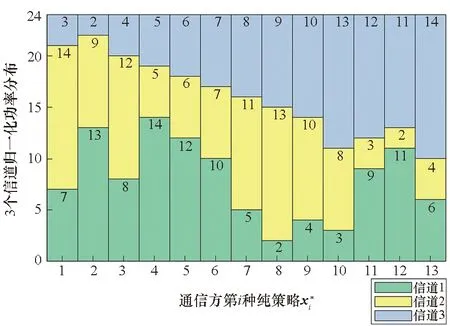
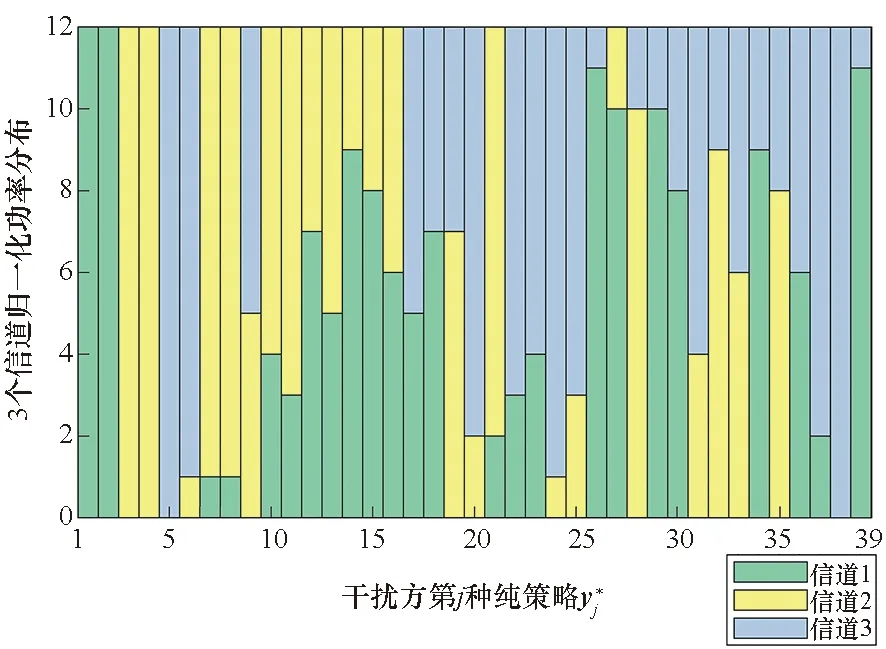

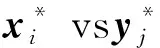
4.2 第2组参数仿真验证结果
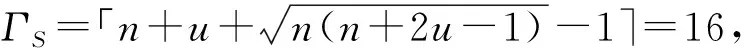
5 结论
