基于CatBoost算法的短期光伏功率预测方法
2023-03-09陈海宏易永利黄珅韩静怡
陈海宏,易永利,黄珅,韩静怡
(1.国网浙江省电力有限公司温州供电公司,浙江 温州 325000;2.亿可能源科技(上海)有限公司,上海 200090)
0 引言
目前,在“双碳”背景下[1],我国正在全力推进光伏发电的大规模开发与高质量发展,光伏发电呈现出良好的发展前景[2-3]。随着集中式光伏发电开发的有序推进,我国在大力推广光伏产业的同时,也在开展光伏发电功率预测相关工作[4]。在电网调度过程中,如果在获得精确的光伏发电功率预测结果的基础上制定生产计划,则能够保障电力系统连续、可靠供电,有效降低发电成本。
但光伏发电功率数据的准确性问题加大了光伏发电功率预测的难度,增加了光伏发电功率预测的不确定性,当光伏电站并网运行时,电力系统的稳定性与经济性会受到影响[5]。可靠的预测算法模型和精细的气象预报数据是准确预测光伏发电功率的决定性因素,而多变的微气象环境使功率预测变得更加复杂,传统的预测方法在建模难度与预测精准度上受到诸多限制。因此,全面了解和掌握先进的光伏发电功率预测方法、利用人工智能算法实现更加精确的光伏发电功率预测,是提升电力系统可靠性与经济性的有效解决方案[6]。
近年来,国内外学者通过不同算法建立模型,提出了多种光伏发电预测方法。刘家庆等[7]借助ARIMA(自回归差分平均)方法和SVR(支持向量机)算法,通过考虑功率修正建立模型从而预测光伏发电功率。李秉晨等[8]基于Kmeans 和CEEMD(完备总体经验模态分解)、PE(排列熵),与LSTM(长短期记忆)神经网络结合建立了用于光伏发电功率预测的模型。刘国海等[9]提出了一种结合注意力机制与GRU(门控循环单元)的Attention-GRU 短期光伏发电功率预测模型。A.I.Salamanis 等[10]提出了一个综合的基准框架,用于多步骤短期光伏发电预测的分析型、数据型和混合型模型。A.A.H.Lateko 等[11]提出了一种基于堆叠集成模型的提前一天到三天的光伏功率预测方法。C.C.Liu 等[12]根据预测过程、需求、时间和空间尺度对预测方法进行分类,罗列出了合适的评价指标。以上算法中,ARIMA等方法对于非线性时序的预测效果较差,而LSTM、GRU算法在模型训练过程中有较多超参数需要考虑,都不能对文字标签进行处理。
本文提出了一种基于CatBoost 算法的短期输出功率预测模型,该方法对于类别型特征有较好的识别能力,且降低了对超参数的要求。结合时间特征、历史光伏功率特征和气象因素特征对未来的光伏发电功率进行预测,同时采用SHAP(SHaplay 加法解释)方法对所构造的特征进行筛选,进一步提高了光伏发电功率预测精度。最后通过实例验证了所提模型在光伏发电短期预测中的优越性和可靠性。
1 光伏发电功率短期预测研究
常用的短期预测方法大致可分为线性预测法、非线性预测法和综合预测法[13]。
1)线性预测法通过结合历史气象数据与历史输出功率数据来预测光伏发电功率。目前大多采用ARMA(自回归移动平均)、ARIMA、ARIMAX(扩展的自回归移动平均)3种方法。
2)受气象因素的影响,光伏发电功率不稳定,为提升预测的精度,可以采用非线性预测法。首先通过对外界影响因素与光伏发电功率的分析,建立非线性模型,进而进行光伏发电功率预测[14]。
3)综合预测法是将非线性预测法与线性预测法相结合产生的预测方法。与单一预测方法相比更为复杂,但预测精度也随之提升。
1.1 预测算法
目前,为实现短期光伏发电的精确预测,提出了时间序列法、回归分析法、SVR、模糊预测法、人工神经网络等。诸多预测方法具有很好的预测精度,但因有过多的超参数调优,并且数据预处理过程中类别变量处理方式较为复杂,容易降低训练速度,影响预测效果。
另外,考虑到气象因素与突发事件对光伏功率预测精度的影响,本文在前期有针对性地收集了光伏电站附近的数值气象预报数据、天气实况数据、光伏电站机组特性数据、检修计划数据、光伏电站出力数据等多种类型数据,训练AI(人工智能)预测模型,预测未来光伏发电出力[2]。由于光伏发电功率具有不平稳、非线性特征,且外围数据中存在较多类别变量(如天气类型等数据),因此本文尝试采用CatBoost 算法建立光电预测模型[15]。
1.1.1 CatBoost算法
CatBoost 和XGBoost、LightGBM 是GBDT(梯度提升树)的主要算法。相比于传统的GBDT,XGBoost算法得到的模型更加简单,LightGBM算法的训练速度更快,而CatBoost 算法的准确率更高。
CatBoost 算法的机器学习参数少,支持类别变量且精度高,在处理类别数据方面具有显著优势,与其他算法相比,准确性更好并提高了泛化能力[16]。在光伏发电功率的预测过程中,可能会出现梯度偏差及预测偏移,从而导致过拟合问题,而CatBoost 恰好能够有效解决该问题。此外,CatBoost算法减少了对广泛的超参数调整的需求,具有很高的鲁棒性。与XGBoost、LightGBM 相比,CatBoost具有以下特点:
1)插入了能够自动将类别型特征处理为数值型特征的新算法。
2)通过组合类别特征处理不同特征的联系,丰富了特征维度。
3)采用排序提升处理数据集的噪声点,解决了预测偏移的问题。
4)采用完全对称树作为基模型,避免了过拟合问题,增加了可靠性,加快了预测进程。
1.1.2 CatBoost特征处理
GBDT 中存在离散的特征(类别型特征),此类特征在算法输入时需要经过处理。最简单的处理方法是Greedy TS,但Greedy TS采用类别特征对应标签的平均值来替换离散特征,当训练数据集与测试数据集的数据结构、数据分布不一致时,标签所替代的离散特征丢失了信息,会导致条件偏移。由此提出采用CatBoost 算法对Greedy TS进行改进[17]。
通过添加先验分布项,使得数据分布免受噪声和低频的影响,即打乱数据集D={(xi.yi)}i=1,…,n顺序,打乱后的序列是σ=(σ1,…,σn),遍历σ1到σn,用遍历到的前p个记录计算类别型特征的数值,具体公式如下:
式中:p为添加的先验项;a为权重系数。
1.1.3 参数优化
在参数优化方面有多种选择,最常用的是Grid Search和它的一些改进方法。
1)Grid Search
GSA(网格搜索算法)是一种穷举搜索,它对输入到搜索空间的每个超参数进行组合。将各个参数的可能取值进行排列组合,列出所有可能的组合“网格”。通过循环遍历,尝试每一种组合,最后选择表现最好的参数组合为每个组合创建一个模型并进行比较。网格搜索是目前比较常见的超参数优化算法,其缺点也很明显:确定最优超参数是一个NP-Hard 问题,因为需要处理的是超参数的组合,所以效率低下。
2)Optuna超参数优化算法
由于Grid Search 没有包含任何结构化的方法来搜索最优超参数集,因此考虑采用新算法对其进行优化,以提高效率。Optuna 超参数调优算法是基于贝叶斯优化算法中的树形帕曾优化器(Parzen)对模型参数进行优化的方法。
Optuna 可以通过不断试错的方法找到最好表现的最优超参数值,具有以下主要特征:可实现分布式并行优化;可修剪无希望调优的试验;通用于多个机器学习框架。
Optuna 主要基于运行的历史数据来确定接下来需要测试的超参数各值的组合。基于已有数据,选择一些超参数组合区域并在该区域中进行超参数搜索尝试。随着不断获取新的结果,它也将更新这一区域并继续搜索。在不断重复搜索、评价更新的过程中获取表现更好的超参数。
Optuna 可以在很复杂的空间中实现超参数优化;可以通过预测终止可能性较小的参数区间,把更多的算力用于可能性更高的区域以提高搜索效率。整体而言,这是一种基于改进贝叶斯的试错算法,当向某一区域尝试得到的效果变差即损失不再减小时停止该区域的搜索,尝试到错误即淘汰,最后选出最优的区域[18]。
1.2 特征工程
通常来说,短期光伏预测需要考虑多种因素,根据这些因素提取相应的特征作为模型的输入,从而提高模型的预测精度。但如果模型考虑了过多不必要的特征,反而容易陷入过拟合,降低模型的准确性;并且过多的特征也会导致模型变得更加复杂,在训练和预测时增加计算耗时。因此,本文提出利用SHAP 方法对模型进行解释,进而得到各个特征重要性,以便在进行特征选择时剔除特征变量中不重要的特征。
1.2.1 SHAP
SHAP 以博弈论思想为基础,用于解释复杂算法中某一个样本各个特征对预测结果产生的影响。SHAP 通过特征的归因值来解释其对模型预测的重要性。归因值为正,代表该特征对模型预测体现正向作用;反之则为负向作用。模型的预测值由模型预测的平均值和特征的归因值相加得到[19]。
如图1所示,根据不同特征对光伏预测影响程度的重要性自上而下排序,红色代表归因值的正向作用,蓝色代表归因值的负向作用。分析可知,历史同时刻负荷、气象数据中的动量通量、长波辐射通量、短波辐射通量、感热通量、云量、空气密度、2 m相对湿度、温度的部分统计量是影响光伏预测性能比较重要的变量。

图1 基于SHAP方法的特征重要性排序Fig.1 SHAP-based ranking of features by the dominance
1.2.2 时间特征
选择合适的时间特征可提高预测的精度。由前文分析可知,光伏发电功率数据具有日、月、季节的周期特性。因此,本文创建了如表1所示的时间特征[20]。

表1 时间特征Table 1 Time characteristics
1.2.3 功率特征
短期光伏预测具有明显的周期性规律,具体体现在:不同日相同采样点间的相似性;不同日之间整体变化规律的相似性;不同周、月、季节的相似性。
同时,受温度等气象因素的影响,光伏具有明显的时滞特性。因此,本文构建了如表2所示的光伏历史数据相关特征。

表2 历史发电功率特征Table 2 Historical generation power characteristics
1.2.4 气象因素特征
利用气象因素,采用更合理的数学模型与算法,可进一步提高光伏预测精度,减小误差。因此,选择的气象数据特征见表3。

表3 气象因素特征Table 3 Characteristics of meteorological factors
1.3 预测流程
开展光伏发电功率预测,首先要通过对现有的光伏历史数据进行数据预处理和相关分析,寻找其在时序上的结构性与规律性;同时分析外围因素(如温度、光照等天气因素)对光伏发电功率预测的影响,利用特征工程建立相应模型。预测流程如图2所示,具体步骤如下:
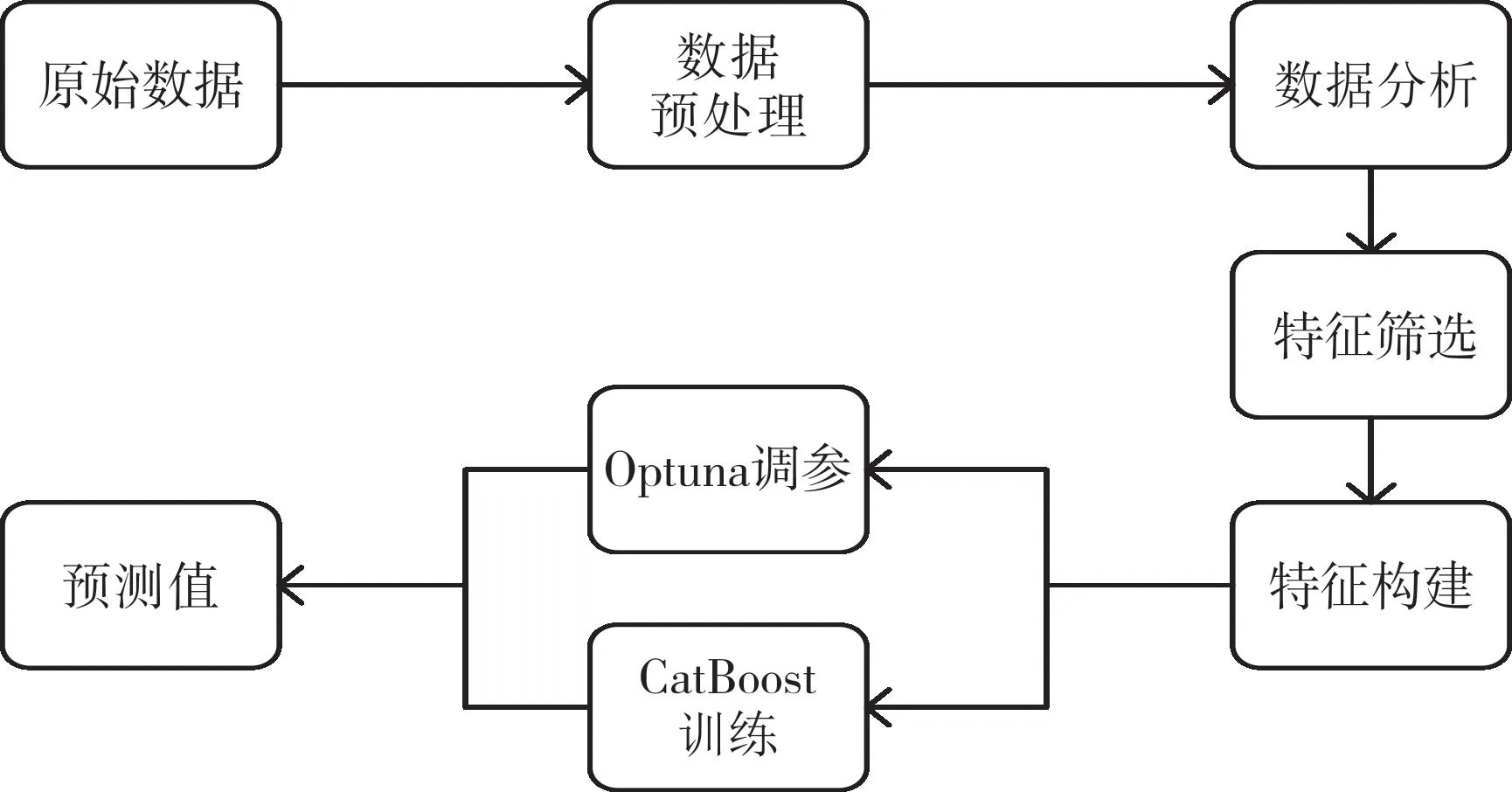
图2 预测流程Fig.2 Prediction flow
1)数据预处理:数据预处理是建立光伏发电功率预测模型的首要步骤。针对光伏以及相关的外围数据,本文考虑采用基于回归的缺失值处理、异常检测、鲁棒统计方法等多种方法对历史数据进行预处理,建立较为完整的预测训练数据集,用于预测模型的训练。
2)功率曲线聚类:功率曲线统计的是多个光伏电站发电功率的总和。通常的聚类方式是根据日期属性(如月、季节等)对数据集进行划分,即相似日方法。本文在实际数据预处理后,通过对数据特性的分析,结合额外因素进行更有针对性的聚类,并在此基础上构造合适的统计特征。
3)历史数据分析:历史数据分析是建立光伏发电功率预测模型的必要条件。本文考虑采用时间序列分析、相关性分析等方法对光伏历史数据及其外围数据进行分析。
4)特征工程:特征工程包括特征选择、特征转化、特征提取等。本文结合分析结果,针对光伏发电功率以及相关数据,利用SHAP 分析方法进行特征筛选。考虑在获得数据后进行详细的探索性分析,进而建立针对本文的功率预测特征集。特征集考虑的数据包括预测区域光伏历史数据和天气预报等数据。
5)模型训练:首先将数据分为训练数据、测试数据,其次训练数据细分为训练集和验证集,测试数据作为测试集。将所选择的特征作为输入,当日光伏发电功率作为输出,利用训练集训练模型,同时利用Optuna 方法优化调整模型参数,构建最佳模型。
6)应用:根据选择的多维特征和训练好的模型对未来光伏发电功率进行预测。
1.4 评价指标
为衡量预测模型的性能优劣,本文采用多种评判方式对模型预测精度进行评估,主要评价指标如式(2)—(5)所示[15,21-22]。
式中:yi为第i时刻的实际采集数据;为第i时刻的预测数据;n为预测值个数;SMAE、SMSE、SRMSE、SR2分别表示光伏样本数据的MAE(平均绝对误差)、MSE(均方误差)、RMSE(均方根误差)、决定系数。
2 算例分析
2.1 实验数据
本文采用某光伏电站2019-01-01 T 00:00 至2020-12-31 T 23:45 的光伏发电功率数据进行分析。该电站额定容量为2.41 MW,系统采样频率为每15 min一次,即一天96个点。选择前80%数据为训练数据,剩余20%数据为测试数据。
首先根据该光伏电站额定容量、扩容信息、限电信息对其历史发电数据进行缺失值、异常值的数据预处理,依据该电站的额定容量、检修信息、扩容信息进行标幺化处理,标幺化基值为可用功率,得到该电站的标幺值(即历史光伏发电功率与可用功率之比),这样可有效避免因训练集时间跨度长而变电站部分检修或扩容导致历史光伏发电功率骤减、骤升,进而影响预测精度。
选取处理后的部分光伏数据示于图3。可以看出,光伏发电功率具有很明显的日周期特性[23]。
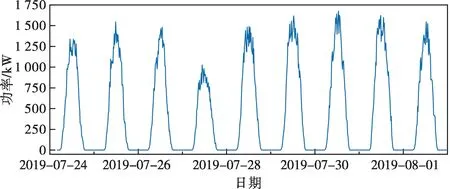
图3 光伏发电功率时序图Fig.3 Sequence diagram of PV generation power
2.2 功率曲线
太阳辐照度是影响光伏电站发电功率的主要因素,具有以年、月、日为周期变化的特性,因此会对光伏发电功率带来相应的周期性变化。因此,本文根据月属性对光伏历史发电功率数据集进行聚合分析,聚合结果如图4所示。
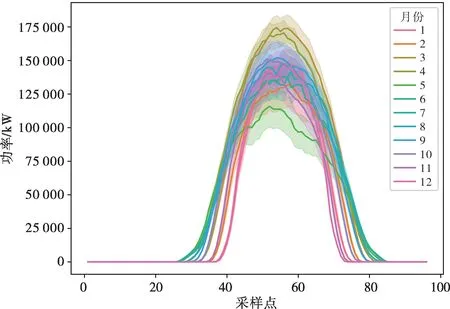
图4 光伏数据按月属性聚合图Fig.4 Diagram of monthly PV data aggregation
图4 的x轴表示采样点,即00:00—24:00 每15 min 采样一次,共96 个采样点。12 条曲线分别是1—12月的月均值曲线。从图4可以看出,光伏发电功率具有明显的日周期特性,出力大致集中在一天中的8:00—16:00,并在12:00—14:00 达到顶峰,太阳落山后光伏出力值为0;从每条曲线非0值宽度可以看出,光伏日发电时长明显随着日照时间长短而改变,冬天最短,夏天最长;从每条曲线高度可以看出,光伏发电功率大小明显随着月份、季节变化,冬天较低,夏天较高。因此光伏发电功率具有明显的日、月、季节周期性特征。
2.3 预测结果分析
根据1.2 节所选择的特征得到如图5 所示预测模型。通过监测历史光伏发电功率、天气数据、时间特征,结合当天天气数据、时间特征以及月度、年度光伏发电功率特征数据,利用CatBoost算法预测当日光伏发电功率。

图5 光伏预测模型结构Fig.5 PV prediction model structure
2.3.1 基于CatBoost算法的预测模型优势
图6是2021年6月某日光伏预测曲线,其中曲线分别是原始光伏曲线和基于DTR(决策树回归)、KNN(K 最邻近)、GBDT、LightGBM、CatBoost 算法的预测结果,均是利用Optuna 方法进行超参数调优后的结果。从图6可以看出,所有模型的预测曲线与原始时序曲线变化趋势均保持一致,但基于CatBoost 算法的模型预测结果更贴近真实曲线。

图6 光伏发电功率预测曲线Fig.6 Diagram of prediction curves of PV generation power
表4为光伏预测评价指标。可以看出,本文所提出的基于CatBoost 算法的光伏预测模型的SRMSE分别比DTR、KNN、GBDT、LightGBM 下降了26.66%、7.5%、22.14%、20%,说明在不同的评价指标下,基于CatBoost 算法的模型预测精度优于其他模型,CatBoost 用于光伏发电功率预测具有很高的精度,适用于真实数据预测。

表4 不同算法的光伏预测误差评价指标对比Table 4 Comparison of PV prediction error evaluation indicators of different algorithms
2.3.2 基于CatBoost算法的模型预测性能
为了验证本文所构建的特征的优异性和有效性,选取以下5种光伏模型进行验证:模型1,考虑近2 天光伏历史数据的CatBoost 算法模型;模型2,考虑近7天光伏历史数据的CatBoost算法模型;模型3,在模型2基础上增加相关时间特性及光伏统计特性的CatBoost 模型;模型4,在模型3上增加天气特征的算法CatBoost模型;模型5,对模型4中特征先根据SHAP值筛选再利用CatBoost预测的模型。
图7为采用5种模型得到的2021年6月某日光伏预测曲线与原始光伏曲线的对比。可以看出,所有模型的预测曲线与原始时序曲线变化趋势保持一致,但模型5的结果更贴近真实曲线。

图7 光伏发电功率预测曲线Fig.7 Prediction curves of PV generation power
表5 列出了不同类型的光伏预测误差评价指标,可以看出,模型5 的SRMSE比模型1—4 分别降低了38.11%、32.15%、19.86%、19.00%,说明本文提出的模型误差评价指标更优,所采用的CatBoost 算法具有很好的预测性能,且提出的先根据SHAP 值特征筛选再利用CatBoost 预测的方法有效提高了预测精度,适用于真实数据预测。
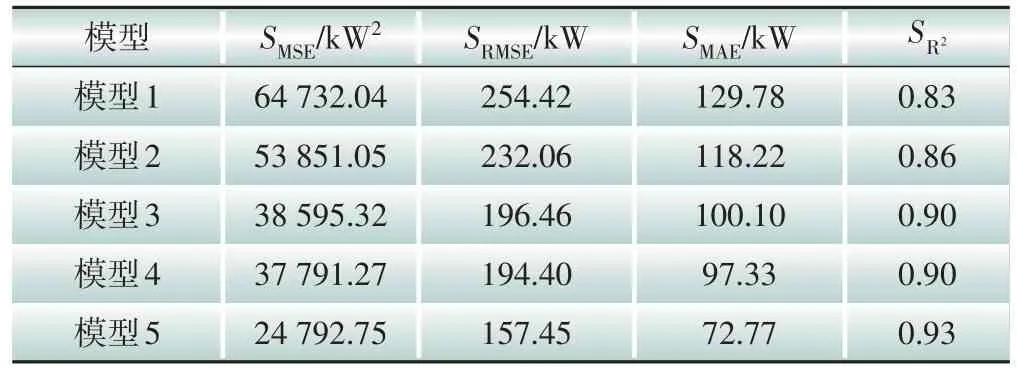
表5 不同类型的光伏预测误差评价指标对比Table 5 Comparison of different evaluation indicators for PV prediction errors
经对比分析,本文提出的基于CatBoost算法、融合多维特征的模型具有很好的预测性能,预测精度较高。本文提出的光伏预测模型SRMSE为157.45 MW,结合案例中光伏额定容量2.41 MW分析知,SRMSE控制在额定容量6.5%左右,而前期调研时了解到国内外同类光伏预测项目的SRMSE与额定容量的比值约为10%,从而说明本文所提光伏预测模型的优越性。
3 结语
在目前构造以新能源为主体的新型电力系统的大背景下,更加准确的光伏发电功率预测技术成为电网规划和电力调度不可或缺的一部分,本文提出了一种基于CatBoost 算法、融合多维特征的预测模型。
1)该模型通过特征之间的联系,使用组合类别特征,丰富了特征维度。CatBoost 还解决了梯度偏差以及预测偏移的问题。
2)利用SHAP 方法进行特征分析筛选,论证了结合光伏发电原理与发电功率特征分析结果的特征筛选对预测精度提升的重要性。
3)通过在同样特征上基于不同的机器学习算法模型的预测精度的对比,证实了基于CatBoost算法的模型具有很好的预测性能。
在进一步提升光伏功率预测精准度的探索中,有两个方向值得重点关注:一是考虑到光伏出力本身的波动性与不确定性,加入实时校正模块,使得在历史数据中训练的模型可以在线自我调节,更适合当前的气象情况;二是可尝试多种模型的组合,使得功率预测能兼顾到各个模型在不同时间段、不同特征上的局部优势,最终得到整体最优的模型和最精准的预测结果。
