Kn□Km,s的r-hued染色

梁玲梅, 刘凤霞, 赖虹建

(1.新疆大学 数学与系统科学学院, 乌鲁木齐 830046; 2.西弗吉尼亚大学 数学系, 美国 西弗吉尼亚 摩根城 26506)

1 引言与主要结果

(i) 对任意边uv∈E(G), 有c(u)≠c(v);

(ii) 对任意顶点v∈V(G), 有|c(NG(v))|≥min{d(v),r}.

对于固定的整数r>0, 图G的r-hued染色数[2-3]是指使图G存在(k,r)-染色的最小正整数k, 记为χr(G).图G的r-hued染色数相关性质可参见文献[4-9].

命题1[9]χr(Kn)=n.

命题2[9]设G是一个图,r≥2, 则χr(G)≥min{Δ(G),r}+1.

设G和H是两个图, 图G与图H的笛卡尔积图是指顶点集为V(G)×V(H)的图, 记为G□H.任意两个顶点(u,v)和(x,y)相邻当且仅当u=x且vy∈E(H)或v=y且ux∈E(G).根据定义知,Δ(G□H)=Δ(G)+Δ(H).

关于两个图的笛卡尔积图的r-hued染色数的研究目前已有很多结果.Suil[10]证明了对任意两个图G和H, 如果δ(G)≥r, 则χr(G□H)≤max{χr(G),χ(H)}; Akbari等[11]分别刻画了路与路、路与圈、圈与圈的笛卡尔积图的2-hued染色数; Kang等[12]证明了如果mn≡2(mod 4), 则χ3(Pn□Pm)=5, 其中Pn表示n个顶点的路; Jahanbekam等[13]刻画了路与路的笛卡尔积图的3-hued染色数和4-hued染色数; Shao等[14]刻画了路与路的平方图的笛卡尔积图的r-hued染色数; Kaliraj等[15]刻画了完全图与星图的笛卡尔积图的2-hued染色数, 以及完全图与轮图的笛卡尔积图的2-hued染色数, 并给出了完全图和完全二部图的笛卡尔积图的2-hued染色数为

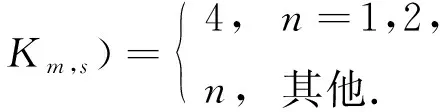
本文将文献[15]的结果推广到更一般的正整数r上, 主要结果如下：

定理1设Kn□Km,s是一个笛卡尔积图,m≥s≥2, 则

2 主要结果的证明

设完全图Kn的顶点集为V(Kn)={v1,v2,…,vn}, 完全二部图Km,s的顶点集为V(Km,s)={u1,u2,…,um,w1,w2,…,ws},m≥s≥2, 由笛卡尔积图的定义, 本文按如下方式记Kn□Km,s的顶点集:

为方便, 记V(Kn□Km,s)=X∪Y, 这里X={viuj|1≤i≤n, 1≤j≤m},Y={viwk|1≤i≤n, 1≤k≤s}.从而可得

(1)

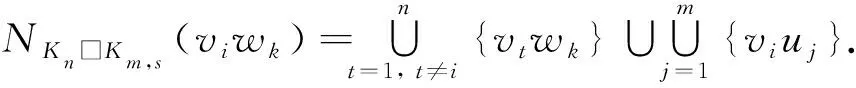
(2)

则有

d(viuj)=n-1+s,d(viwk)=n-1+m,

Δ(Kn□Km,s)=Δ(Kn)+Δ(Km,s)=n-1+m.

本文约定用n×(m+s)阶矩阵的各元素表示V(Kn□Km,s)对应顶点的染色.

定理2假设r

证明： 由于Kn□Km,s总包含Kn, 因此由命题1有χr(Kn□Km,s)≥χr(Kn)=n.

下面给出Kn□Km,s的一个具体(n,r)-染色, 以此说明χr(Kn□Km,s)≤n.定义映射c1:V(Kn□Km,s)→{1,2,3,…,n}为

即c1(V(Kn□Km,s))=A.由矩阵A知, 当i≠t时,c1(viuj)≠c1(vtuj),c1(viwk)≠c1(vtwk),c1(viuj)≠c1(viwk), 且A中每个元素都满足1≤aij≤n, 因此c1是Kn□Km,s的一个n-染色.下面证明映射c1满足条件(ii).对于viuj∈X这类顶点, 由式(1)可得|NKn□Km,s(viuj)|=n-1+s, 而s≥2,n>r, 因此d(viuj)=n-1+s>r.当1≤i≤n-1时,c1(NKn□Km,s(viuj))={1,2,…,n}{i+1}; 当i=n时,c1(NKn□Km,s(viuj))={2,3,…,n}.从而

|c1(NKn□Km,s(uivj))|=n-1≥min{d(viuj),r}=min{n-1+s,r}=r.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m>r.又因为c1(NKn□Km,s(viwk))={1,2,…,n}{i}, 所以

|c1(NKn□Km,s(viwk))|=n-1≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c1是Kn□Km,s的一个(n,r)-染色, 故χr(Kn□Km,s)≤n.综上所述,χr(Kn□Km,s)=n.证毕.

下面总假设r≥n.根据r与图Kn□Km,s的最大度和最小度的大小关系分类讨论.当r小于Kn□Km,s的最小度时, 有如下结论.

定理3假设r

情形1)r-n+1≤n.

对于顶点viu1∈X, 要满足条件(ii), 则有

|c(NKn□Km,s(viu1))|≥min{d(viuj),r}=min{n-1+s,r}=r,

故viu1的邻点集至少可染r种不同颜色, 由于viu1在Kn中, 所以满足正常染色时该点邻点在X中已有(n-1)种不同颜色, 因此在Y中的邻点至少有(r-n+1)种颜色.用W1,W2,…,Wr-n+1,…,Ws表示Kn在Kn□Km,s中Y部分的第1,2,3,…,r-n+1,…,s个拷贝, 于是可任意调整顺序, 不妨设前(r-n+1)个是用来满足X中顶点条件(ii)的.对于X中第一列顶点, 由于在Kn中, 不妨设染色为c(viu1)=i(1≤i≤n), 因此要使点v1u1满足条件(ii), 则W1中的顶点c(v1w1)∉{1,2,3,…,n}, 不妨设c(v1w1)=n+1.要使点v2u1满足条件(ii), 由v1w1与v2w1在W1中可知,W1中的顶点c(v2w1)∉{1,2,3,…,n,n+1}, 不妨设c(v2w1)=n+2.同理c(v3w1)∉{1,2,3,…,n,n+1,n+2}, 不妨设c(v3w1)=n+3.以此类推, 可设c(vnw1)=2n.故V(Kn□Km,s)至少需要2n种不同颜色, 即χr(Kn□Km,s)≥2n.

下面给出Kn□Km,s的一个(2n,r)-染色, 以此说明χr(Kn□Km,s)≤2n.定义映射c2:V(Kn□Km,s)→{1,2,3,…,2n}如下:

即c2(V(Kn□Km,s))=B=B1∪B2, 这里B1是X中顶点的染色方式,B2是Y中顶点的染色方式.由矩阵B可知, 当i≠t时,c2(viuj)≠c2(vtuj),c2(viwk)≠c2(vtwk),c2(viuj)≠c2(viwk), 且B中每个元素都满足1≤bij≤2n, 因此c2是Kn□Km,s的一个2n-染色.

下面证明映射c2满足条件(ii).对于viuj∈X这类顶点, 由式(1), 有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s>r.由矩阵B可知, 顶点viuj的邻点集在X中有(n-1)种不同颜色属于{n+1,n+2,…,2n}, 在Y中有(r-n+1)种不同颜色属于{1,2,…,n}, 从而

|c2(NKn□Km,s(uivj))|=n-1+(r-n+1)=r≥min{d(viuj),r}=min{n-1+s,r}=r.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m≥n-1+s>r.由矩阵B可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,n}, 在X中有(r-n+1)种不同颜色属于{n+1,n+2,…,2n}, 从而

|c2(NKn□Km,s(viwk))|=r≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c2是Kn□Km,s的一个(2n,r)-染色, 即χr(Kn□Km,s)≤2n.综上所述,χr(Kn□Km,s)=2n.

情形2)r-n+1>n.

对于顶点v1uj∈X, 要满足条件(ii), 则

|c(NKn□Km,s(v1uj))|≥min{d(v1uj),r}=min{n-1+s,r}=r,

故v1uj的邻点集至少可染r种不同颜色.由于v1uj在Kn中, 所以满足正常染色时v1uj的X中邻点已有(n-1)种不同颜色, 因此在Y中的邻点, 即Y的第一行顶点至少需要(r-n+1)种颜色.对于顶点v1wk∈Y, 由条件(ii), 有

|c(NKn□Km,s(v1wk))|≥min{d(v1wk),r}=min{n-1+m,r}=r,

故v1wk的邻点集至少可染r种不同颜色, 由于v1wk在Kn中, 所以满足正常染色时v1wk的Y中邻点已有(n-1)种不同颜色, 因此在X中的邻点, 即X的第一行顶点至少需要(r-n+1)种颜色.又因为同一行顶点是完全二部图的顶点, 故X和Y中第一行顶点染色必须不同, 于是V(Kn□Km,s)的第一行至少需要2(r-n+1)种不同颜色, 从而V(Kn□Km,s)至少需要2(r-n+1)种不同颜色, 即χr(Kn□Km,s)≥2(r-n+1).

下面给出Kn□Km,s的一个(2(r-n+1),r)-染色, 以此说明χr(Kn□Km,s)≤2(r-n+1).定义映射c3:V(Kn□Km,s)→{1,2,3,…,2(r-n+1)}如下:

即c3(V(Kn□Km,s))=C=C1∪C2, 这里:C1是X中顶点的染色方式, 该矩阵元素均小于等于2(r-n+1), 若有元素大于2(r-n+1), 则从r-n+2重新开始循环;C2是Y中顶点的染色方式, 该矩阵元素均小于等于 (r-n+1), 若有元素大于(r-n+1), 则重新从1开始循环.由矩阵C可知, 当i≠t时,c3(viuj)≠c3(vtuj),c3(viwk)≠c3(vtwk),c3(viuj)≠c3(viwk), 且C中每个元素都满足1≤cij≤2(r-n+1), 因此c3是Kn□Km,s的一个2(r-n+1)-染色.

下面证明映射c3满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s≥r.由矩阵C可知, 顶点viuj的邻点集在X中有(n-1)种不同颜色属于{r-n+1+1,r-n+1+2,…,2(r-n+1)}, 在Y中有(r-n+1)种不同颜色属于{1,2,…,r-n+1}, 从而

|c3(NKn□Km,s(uivj))|=r≥min{d(viuj),r}=min{n-1+s,r}=r.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m>r.由矩阵C可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,r-n+1}, 在X中有(r-n+1)种不同颜色属于{r-n+1+1,r-n+1+2,…,2(r-n+1)}, 于是

|c3(NKn□Km,s(viwk))|=r≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c3是Kn□Km,s的一个(2(r-n+1),r)-染色, 即χr(Kn□Km,s)≤2(r-n+1).综上所述,χr(Kn□K1,s)=2(r-n+1).证毕.

当r介于Kn□Km,s的最小度和最大度之间时, 有如下结论.

定理4假设n-1+s≤r≤n-1+m, 则χr(Kn□Km,s)=max{2n,r+1,s+r-n+1}.

情形1)n≥s.

①n≥r-n+1.对于顶点viu1∈X, 要满足条件(ii), 则

|c(NKn□Km,s(viu1))|≥min{d(viu1),r}=min{n-1+s,r}=n-1+s,

故viu1的邻点集至少可染(n-1+s)种不同颜色, 由于viu1在Kn中, 所以满足正常染色时该点邻点在X中已有(n-1)种不同颜色, 因此在Y中的邻点至少要贡献s种颜色, 于是Y中第一行元素必须与X中第一列元素不同.由于X中第一列顶点在Kn中, 不妨设染色为c(viu1)=i(1≤i≤n).用W1,W2,…,Ws表示Kn在Kn□Km,s中Y部分的第1,2,3,…,s个拷贝, 因此W1中的顶点c(v1w1)∉{1,2,3,…,n}, 不妨设c(v1w1)=n+1.要使v2u1满足条件(ii), 由v1w1与v2w1在W1中可知,W1中的顶点c(v2w1)∉{1,2,3,…,n,n+1}, 不妨设c(v2w1)=n+2.同理c(v3w1)∉{1,2,3,…,n,n+1,n+2}, 不妨设c(v3w1)=n+3.以此类推, 可设c(vnw1)=2n.故V(Kn□Km,s)至少需要2n种不同颜色, 即χr(Kn□Km,s)≥2n.

下面给出Kn□Km,s的一个(2n,r)-染色, 以此说明χr(Kn□Km,s)≤2n.定义映射c4:V(Kn□Km,s)→{1,2,3,…,2n}如下:

即c4(V(Kn□Km,s))=D.由矩阵D知, 当i≠t时,c4(viuj)≠c4(vtuj),c4(viwk)≠c4(vtwk),c4(viuj)≠c4(viwk), 且D中每个元素都满足1≤dij≤2n, 因此c4是Kn□Km,s的一个2n-染色.下面证明映射c4满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s≤r.由矩阵D可知, 顶点viuj的邻点集在X中有(n-1)种不同颜色属于{n+1,n+2,…,2n}, 在Y中有s种不同颜色属于{1,2,…,n}, 从而

|c4(NKn□Km,s(uivj))|=n-1+s≥min{d(viuj),r}=min{n-1+s,r}=n-1+s.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viuj)=n-1+m>r.又由矩阵D可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,n}, 在X中有(r-n+1)种不同颜色属于{n+1,n+2,…,2n}, 于是

|c(NKn□Km,s(viwk))|=r≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c4是Kn□Km,s的一个(2n,r)-染色, 即χr(Kn□Km,s)≤2n.综上所述,χr(Kn□Km,s)=2n.

②n

χr(Kn□Km,s)≥min{Δ(Kn□Km,s),r}+1=min{n-1+m,r}+1=r+1.

下面给出Kn□Km,s的一个(r+1,r)-染色, 以此说明χr(Kn□Km,s)≤r+1.定义映射c5:V(Kn□Km,s)→{1,2,3,…,r+1}如下:

即c(V(Kn□Km,s))=E.由矩阵E知, 当i≠t时,c5(viuj)≠c5(vtuj),c5(viwk)≠c5(vtwk),c5(viuj)≠c5(viwk), 且E中每个元素都满足1≤eij≤r+1, 因此c5是Kn□Km,s的一个(r+1)-染色.下面证明映射c5满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s≤r.由矩阵E可知, 顶点viuj的邻点集在X中有(n-1)种不同颜色属于{n+1,n+2,…,n+r-n+1}, 在Y中有s种不同颜色属于{1,2,…,n}, 从而

|c5(NKn□Km,s(uivj))|=n-1+s≥min{d(viuj),r}=min{n-1+s,r}=n-1+s.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m>r.又由矩阵D可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,n}, 在X中有(r-n+1)种不同颜色属于{n+1,n+2,…,n+r-n+1}, 从而

|c5(NKn□Km,s(viwk))|=r≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c5是Kn□Km,s的一个(r+1,r)-染色, 即χr(Kn□Km,s)≤r+1.综上所述,χr(Kn□Km,s)=r+1.

情形2)n

若n≥r-n+1, 则r-n+1

|c(NKn□Km,s(v1uj))|≥min{d(v1uj),r}=min{n-1+s,r}=n-1+s,

故v1uj的邻点集至少可染(n-1+s)种不同颜色, 由于v1uj在Kn中, 所以满足正常染色时在X中已有(n-1)不同颜色, 因此在Y中的第一行顶点至少需要s种颜色.对于顶点v1wk∈Y, 要满足条件(ii), 则

|c(NKn□Km,s(v1wk))|≥min{d(v1wk),r}=min{n-1+m,r}=r,

故v1wk的邻点集至少可染r种不同颜色, 由于v1wk在Kn中, 所以满足正常染色时在Y中已有(n-1)种不同颜色, 因此在X中的第一行顶点至少需要(r-n+1)种颜色.又因为同一行顶点是完全二部图的顶点, 故第一行X和Y中顶点染色必须不同, 于是V(Kn□Km,s)的第一行至少需要(s+(r-n+1))种不同颜色, 因此V(Kn□Km,s)至少需要(s+(r-n+1))种不同颜色, 即χr(Kn□Km,s)≥s+(r-n+1).

下面给出Kn□Km,s的一个(s+r-n+1,r)-染色, 以此说明χr(Kn□Km,s)≤s+r-n+1.定义映射c6:V(Kn□Km,s)→{1,2,3,…,s+r-n+1}如下:

即c6(V(Kn□Km,s))=F.由矩阵F知, 当i≠t时,c6(viuj)≠c6(vtuj),c6(viwk)≠c6(vtwk),c6(viuj)≠c5(viwk), 且F知中每个元素都满足1≤fij≤s+r-n+1, 因此c6是Kn□Km,s的一个(s+r-n+1)-染色.

下面证明映射c6满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s≤r.由矩阵F可知, 顶点viuj的邻点集在X中有(n-1)种不同颜色属于{s+1,s+2,…,s+r-n+1}, 在Y中有s种不同颜色属于{1,2,…,s}, 则

|c6(NKn□Km,s(uivj))|=n-1+s≥min{d(viuj),r}=min{n-1+s,r}=n-1+s.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m>r.又由矩阵F可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,s}, 在X中有(r-n+1)种不同颜色属于{s+1,s+2,…,s+r-n+1}, 从而

|c6(NKn□Km,s(viwk))|=r≥min{d(viwk),r}=min{n-1+m,r}=r.

因此c6是Kn□Km,s的一个(s+r-n+1,r)-染色, 即χr(Kn□Km,s)≤s+r-n+1.综上所述,χr(Kn□Km,s)=s+r-n+1.证毕.

当r大于Kn□Km,s的最大度时, 有如下结论.

定理5假设r>n-1+m, 则χr(Kn□Km,s)=max{2n,n+m,s+m}.

情形1)n≥s.

①n≥m.对于顶点viu1∈X, 要满足条件(ii), 则

|c(NKn□Km,s(viu1))|≥min{d(viu1),r}=min{n-1+s,r}=n-1+s,

故viu1的邻点集至少可染(n-1+s)种不同颜色, 由于viu1在Kn中, 所以满足正常染色时该点邻点在X中已有(n-1)种不同颜色, 因此在Y中的邻点至少贡献s种颜色.用W1,W2,…,Ws表示Kn在Kn□Km,s中Y部分的第1,2,3,…,s个拷贝, 则W1,W2,…,Ws中的顶点染色要满足X中顶点的条件(ii), 对于X中第一列顶点, 由于在Kn中, 不妨设染色为c(viu1)=i(1≤i≤n), 因此要满足v1u1的条件(ii), 则W1中的顶点c(v1w1)∉{1,2,3,…,n}, 不妨设c(v1w1)=n+1.要满足v2u1的条件(ii), 由v1w1与v2w1在W1中可知,W1中的顶点c(v2w1)∉{1,2,3,…,n,n+1}, 不妨设c(v2w1)=n+2.同理c(v3w1)∉{1,2,3,…,n,n+1,n+2}, 不妨设c(v3w1)=n+3.以此类推, 可设c(vnw1)=2n.因此V(Kn□Km,s)至少需要2n种不同颜色, 即χr(Kn□Km,s)≥2n.

下面给出Kn□Km,s的一个(2n,r)-染色, 以此说明χr(Kn□Km,s)≤2n.定义映射c7:V(Kn□Km,s)→{1,2,3,…,2n}如下:

即c7(V(Kn□Km,s))=G.由矩阵G知, 当i≠t时,c7(viuj)≠c7(vtuj),c7(viwk)≠c7(vtwk),c7(viuj)≠c7(viwk), 且G中每个元素都满足1≤gij≤2n, 因此c7是Kn□Km,s的一个2n-染色.

下面证明映射c7满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s

|c7(NKn□Km,s(viuj))|=n-1+s≥min{d(viuj),r}=min{n-1+s,r}=n-1+s.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m≤r.又由矩阵G可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,n}, 在X中有m种不同颜色属于{n+1,n+2,…,2n}, 从而

|c7(NKn□Km,s(viwk))|=n-1+m≥min{d(viwk),r}=min{n-1+m,r}=n-1+m.

因此c7是Kn□Km,s的一个(2n,r)-染色, 即χr(Kn□Km,s)≤2n.综上所述,χr(Kn□Km,s)=2n.

②n

χr(Kn□Km,s)≥min{Δ(Kn□Km,s),r}+1=min{n-1+m,r}+1=n+m.

下面给出Kn□Km,s的一个(n+m,r)-染色, 以此说明χr(Kn□Km,s)≤n+m.定义映射c8:V(Kn□Km,s)→{1,2,3,…,n+m}如下:

即c8(V(Kn□Km,s))=H.由矩阵H知, 当i≠t时,c8(viuj)≠c8(vtuj),c8(viwk)≠c8(vtwk),c8(viuj)≠c8(viwk), 且H中每个元素都满足1≤hij≤n+m.因此c8是Kn□Km,s的一个(n+m)-染色.

下面证明映射c8满足条件(ii).对于viuj∈X这类顶点, 由式(1)可知, |NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s

|c8(NKn□Km,s(viuj))|=n-1+s≥min{d(viuj),r}=min{n-1+s,r}=n-1+s.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m≤r.又由矩阵G可知, 顶点viwk的邻点集在Y中有(n-1)种不同颜色属于{1,2,…,n}, 在X中有m种不同颜色属于{n+1,n+2,…,n+m}, 从而

|c8(NKn□Km,s(viwk))|=n+m-1≥min{d(viwk),r}=min{n-1+m,r}=n-1+m.

因此c8是Kn□Km,s的一个(n+m,r)-染色, 即χr(Kn□Km,s)≤n+m.综上所述,χr(Kn□Km,s)=n+m.

情形2)n

已知s≤m, 因此n

|c(NKn□Km,s(v1uj))|≥min{d(v1uj),r}=min{n-1+s,r}=n-1+s,

故v1uj的邻点集至少可染(n-1+s)种不同颜色, 由于v1uj在Kn中, 所以满足正常染色时邻点集在X中已有(n-1)种不同颜色, 因此在Y中的第一行顶点至少需要s种颜色.对于顶点v1wk∈Y, 要满足条件(ii), 则

|c(NKn□Km,s(v1wk))|≥min{d(v1wk),r}=min{n-1+m,r}=n-1+m,

故v1wk的邻点集至少可染(n-1+m)种不同颜色, 由于v1wk在Kn中, 所以满足正常染色时邻点集在Y中已有(n-1)种不同颜色, 因此第一行在X中的顶点至少需要m种颜色.又因为同一行顶点是完全二部图的顶点, 故第一行X和Y中顶点染色必须不同, 于是V(Kn□Km,s)的第一行至少需要(s+m)种不同颜色, 因此V(Kn□Km,s)至少需要(s+m)种不同颜色, 即χr(Kn□Km,s)≥s+m.

下面给出Kn□Km,s的一个(s+m,r)-染色, 以此说明χr(Kn□Km,s)≤s+m.定义映射c9:V(Kn□Km,s)→{1,2,3,…,s+m}如下:

即c9(V(Kn□Km,s))=P.由矩阵P知, 当i≠t时,c9(viuj)≠c9(vtuj),c9(viwk)≠c9(vtwk),c9(viuj)≠c9(viwk), 且P中每个元素都满足1≤pij≤s+m, 因此c9是Kn□Km,s的一个(s+m)-染色.

下面证明c9满足条件(ii).对于viuj∈X这类顶点, 由式(1)有|NKn□Km,s(viuj)|=n-1+s, 则d(viuj)=n-1+s

|c9(NKn□Km,s(uivj))|=n+s-1≥min{d(viuj),r}=min{n-1+s,r}=n+s-1.

对于viwk∈Y这类顶点, 由式(2)可得|NKn□Km,s(viwk)|=n-1+m, 则d(viwk)=n-1+m

|c9(NKn□Km,s(viwk))|=n+m-1≥min{d(viwk),r}=min{n-1+m,r}=n+m-1.

因此c9是Kn□Km,s的一个(s+m,r)-染色, 即χr(Kn□Km,s)≤s+m.综上所述,χr(Kn□Km,s)=s+m.

由定理2～定理5即可证得定理1.