刚度等效在地坑过滤器滞留篮抗震分析中的应用

兰天宝，董娇娇，彭星铭，盛锋

重大工程装备

刚度等效在地坑过滤器滞留篮抗震分析中的应用

兰天宝，董娇娇，彭星铭，盛锋

（中国核电工程有限公司，北京 100840）

对地坑过滤器滞留篮的过滤板进行刚度等效计算。应用能量法和各向异性法对地坑过滤器滞留篮的过滤板进行等效刚度计算。基于变形能相等的能量法得到的频率远大于地震反应谱的截止频率，该方法适用于滞留篮模型的工程要求。基于各向异性法得到的主频率与实际模型主频率相差14%，该方法同样适用于滞留篮的工程要求。2种方法均可满足工程要求，各向异性方法更接近实际模型。最终采用基于能量法的模型和各项异性刚度等效过滤板都取得了较好的效果。

地坑过滤器；滞留篮；过滤板；等效；抗震分析

在压水堆核电事故的分析中，一些假想的极限事故（如主管道破裂、主蒸汽管道破裂等）如果发生在安全壳内，会引发安注、安全壳喷淋的动作，最终从主系统喷射出来的水、安注水、喷淋水都会进入安全壳底部，被收集在一个称为地坑的大水池中[1-3]。为保证应急堆芯冷却系统的正常运行，需要在安全壳底层设置地坑过滤器[4]，其主要功能是依靠自身滤网对事故工况下的碎片进行拦截，来保障冷却系统和喷淋系统的正常运行。压水堆核电站安全壳地坑过滤器在电厂严重事故工况下为防止堆芯融化，保证安全壳的完整性起着关键作用，核电规范设计要求对地坑过滤器事故工况下的应力有相应的要求[5-6]。

滞留篮是地坑过滤器的关键设备之一，破口或事故喷发的流体夹带安全壳内的碎渣全部流入滞留篮内，经过滞留篮过滤板的过滤，大部分碎渣留在滞留篮内[7]。地坑过滤器滞留篮由钢结构框架和过滤板构成，过滤板为三明治结构，上下2层为带穿孔的平板，由中间筋板连接固定，过滤板结构如图1所示。过滤板和钢结构框架尺寸细节相差较大，按照过滤板细节进行建模耗时、费力，因此在评估滞留篮抗震性能时，需要将过滤板进行简化，等效为平板。采用反应谱法对滞留篮进行抗震分析计算，由于滞留篮浸没在水中，若过于保守地简化，较大的附加水质量将会使得设计变得冗余笨重[8-9]，因此在计算时怎样将过滤板进行简化使其能逼近实际模型的刚度，是一个难点问题。

图1 过滤板结构

1 基于变形能等效的能量法

目前关于刚度等效的方法主要分2种[10]：第1种为平衡方程等效法，即直接利用等效后的板与筋板载荷和位移曲线协调一致，适合加筋板的结构等效，工程上有相关经验公式，适合结构简单的模型，较为成熟；第2种方法为基于能量法的变形能一致的刚度等效。第2种方法应用广泛，适合三明治结构类型的等效。首先从变形能等效原理出发，导出将过滤板等效为无肋板的等效刚度计算公式。

1.1 刚度等效的适用

对于使用刚度等效法应充分考虑其适用情形，刚度等效法是为了简化结构的一种等效方法，无法保证与原结构完全一致，需要考虑假设前提对该方法的影响，如等效后的结构变形与原结构相差较大，需要谨慎考虑该方法。如将一个突然变径的杆进行等效成粗细均匀的杆（如图2所示），其挠曲线是不同的，导致其临界力不同，尤其是当变径杆截面尺寸变化较大的情况下，即底部杆的刚度比上部细杆大很多，等效刚度法带来的误差更大[11]。

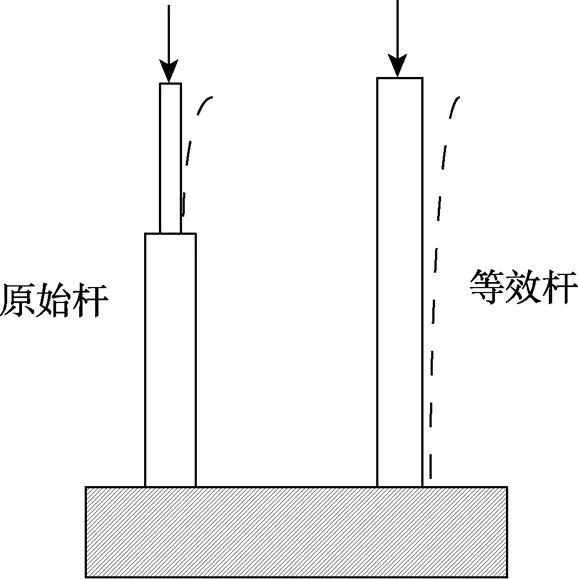
图2 杆的等效示意

将过滤板结构等效为单层板，无法展现模型的局部细节，但对于整体模型来说，并不会影响结构的整体振型和钢结构应力、基础载荷等。当需要对过滤板局部应力（如加强筋的应力）进行分析时，可建立局部细节模型分析。因此，采用刚度等效法适用于滞留篮整体模型的抗震分析。

1.2 能量法计算刚度等效

对于能量法计算等效刚度的研究已经十分成熟[12-15]，相关研究给出了理论和公式，见式（1）、（2）。理论推理过程的基本假设是：具有相同平面尺寸的加肋板和无肋板在相同荷载的作用下具有相同的弹性变形能，根据虚功原理，外力所做的功恒等于加肋板变形后板内积蓄的变形能a。同理，无肋板在外力所做的功恒等于板变形后板内积蓄的变形能b，过程如图3所示。

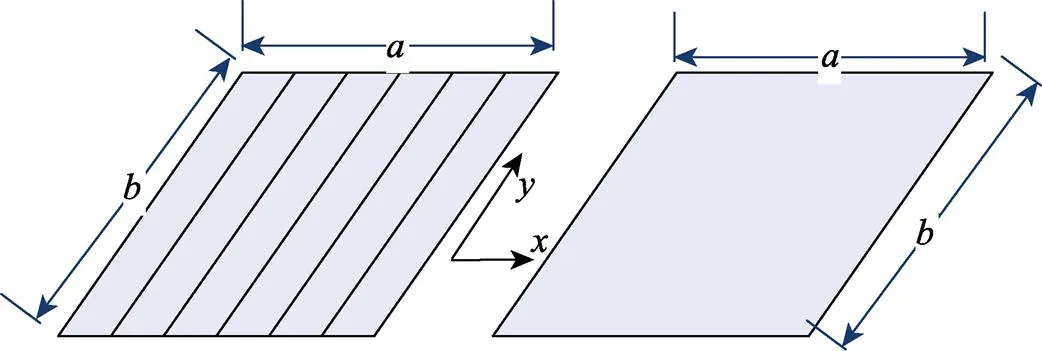
图3 肋板和无肋板的等效

根据假设：ab，假设两板具有相同的挠曲函数a(,)=b(,)=(,)，即肋板与无肋板的刚度相同，变形相同。对于a板，变形能由板和肋共同贡献，见式（3）。

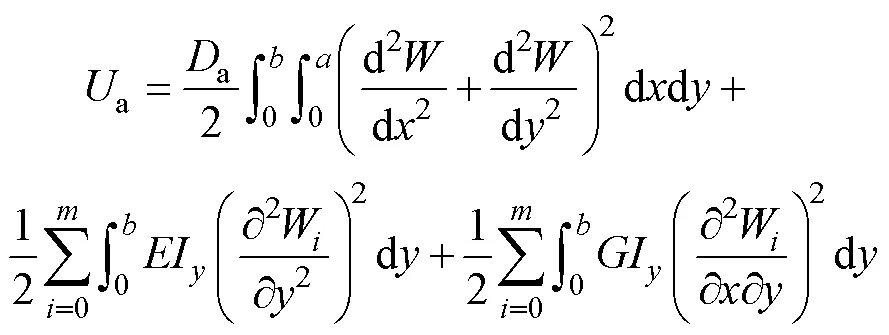
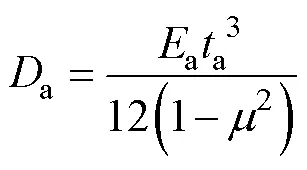
对于等效的b板，其弹性变形能为：

根据式（5）进一步计算板的频率：

根据以上公式，求得等效后板的频率为118 Hz。经分析得，若单方向加肋板，在2个方向的抗弯刚度是不同的，仅通过修改等效板的厚度并不能表征这种特性。本文使用的基于变形能相等的方法平均了2个方向的抗弯刚度，并且假设了挠曲函数，而实际的模型变形形态可能比试函数更复杂，忽略了剪切变形能，因此会与实际模型存在较大误差，低于实际模型的频率[16]。但是根据等效板厚得出的频率远大于地震反应谱的截止频率，该方法对于滞留篮模型可以满足工程要求。

2 各向异性刚度矩阵法

弹性体如果在各个方向的弹性都相同，称为各向同性体[17]；如果在各个方向的弹性并不完全相同，则称为各向异性体。对于各向异性的薄板研究表明，板的2个方向的尺寸、两向刚度及扭转刚度对板的频率均有直接影响[18]。对于加肋板，虽然可以用能量法计算它们的自然频率和临界载荷，但计算非常复杂[19]，将加肋条平板中肋条的刚度归入平板的刚度，从而把具有肋条的各向同性板变换为不具有肋条的各向异性板，则计算大为简化[20]。

为了进一步逼近实际模型，考虑板的横向剪切的板壳广义应力和应变的关系为：

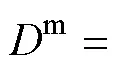
因此各向异性板的薄膜和弯曲刚度矩阵表示为：

式中：1212为截面力；1212为截面弯矩。

根据参考文献[21]，加肋板的抗弯刚度在沿着肋筋的方向可表示为：

式中：Ir为从肋板截面取出的某列（如图4所示）沿板中心线的惯性矩。另一方向的惯性矩，考虑为三明治层合板，将中间层弹性模量设为接近0。根据文献[21]，各向异性板的扭转刚度H为：

式中：0为无肋时板的抗弯刚度；为剪切模量；为肋肋的抗扭惯性矩。

3 验证与分析

为了对2种方法进行刚度等效后的计算结果进行验证，建立滞留篮过滤板的实际模型[22]。由于实际模型模态存在局部细节的肋板振型，但参与质量较小，因此选取参与质量较大的模态振型分析，将实际模型得到的计算主频率与以上2种方法得到的主频率进行对比，见表1。

表1 主频率对比

Tab.1 Comparison of main frequencies

实际模型主频率模态振型如图5所示，基于各向异性法对过滤板进行简化后计算得到的主频率模态振型如图6所示。可以看出，实际模型和各向异性法等效后的模型计算结果整体趋势相似，应力最大、最小值出现的位置相似。各向异性法计算的主频率为263 Hz，相较实际模型计算的主频率误差为14%，计算的主频率均已远超过地震谱的截止频率，认为该计算可以符合工程要求，且较基于变形能一致的能量法等效更接近于实际模型计算结果，该方法更适合在工程计算中用于对滞留篮过滤板进行刚度等效。

由于能量法假定了变形挠曲函数，忽略了层间剪切能量，考虑综合等效，因此相对过滤板实际模型的误差较大。刚度等效将实际几何模型包含的多层板简单等效为一层板，会丢失一些模态振型，如上下两层板的相离运动等一些振型，如图7所示。这是由于模型简化导致的，实际模型的质量分布也和等效后的板存在差异。因此，当需要重点关注过滤板的应力状态时[23]，则需要进行局部的模型应力分析，建立肋板符合实际的模型。工程上既要考虑进度更关注精度，在进行模型等效时，需要评估等效后带来的误差。

图5 实际模型主频率模态振型

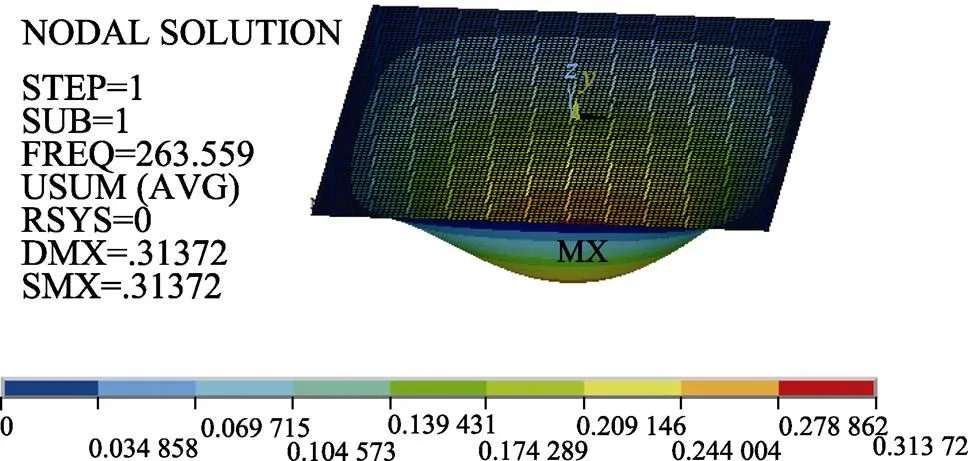
图6 各向异性法主频率模态振型

图7 过滤板的模态振型

滞留篮模型的整体尺寸约为7 000 mm×3 000 mm× 3 000 mm，由于板的刚度较大，对于采用等效板来建模获取梁的弯矩、轴力、剪力等和基础载荷是可行的。建立如图8所示的滞留篮有限模型，应用谱分法[24-25]对滞留篮进行抗震分析。在整体模型中，用各向异性法对过滤板进行刚度等效简化，过滤板的应力状态采用局部模型进行分析。

图8 滞留篮有限元模型

4 结论

本文阐述了刚度等效法的原理和适用条件，对比了能量法和各向异性2种方法在计算地坑过滤器滞留篮过滤板的结果区别，并根据实际模型对2种方法进行了验证，结果表明：

1）基于变形能相等的能量法和各向异性法对滞留篮过滤板的刚度等效计算均可满足工程要求，各向异性方法更接近实际模型。

2）由于几何上的简化和质量的分布会导致等效后的模型与实际模型存在偏差，使用刚度等效法应评估这种影响，最终本文采用各向异性法完成了滞留篮的抗震分析。

[1] 李春, 张庆华, 常猛, 等. 先进压水堆核电厂安全壳地坑滤网设计[J]. 核安全, 2012, 11(1): 61-64.

LI Chun, ZHANG Qing-hua, CHANG Meng, et al. The Containment Sump Screen Design in Advanced PWR NPPS[J]. Nuclear Safety, 2012, 11(1): 61-64.

[2] 路广遥, 任俊生, 向文元, 等. 大型压水堆核电站地坑过滤器发展及应用[J]. 电力与能源, 2011, 32(5): 389-391.

LU Guang-yao, REN Jun-sheng, XIANG Wen-yuan, et al. Development and Application of Containment Sump Strainer in PWR[J]. Power & Energy, 2011, 32(5): 389-391.

[3] 张卫, 龚钊, 朱京梅, 等. 秦山核电二期扩建工程安全壳地坑过滤器设计改进及遗留问题分析[J]. 核动力工程, 2013, 34(6): 128-131.

ZHANG Wei, GONG Zhao, ZHU Jing-mei, et al. Design Improvement and Open Item Analysis of Containment Sump Strainer in QINSHAN Phase II Extension Project[J]. Nuclear Power Engineering, 2013, 34(6): 128-131.

[4] 刘夏杰, 王德忠, 张臣刚, 等. 核电厂地坑过滤器附加质量试验研究[J]. 核动力工程, 2012, 33(1): 14-18.

LIU Xia-jie, WANG De-zhong, ZHANG Chen-gang, et al. Experimental Study on Added Mass of Sump Strainer in Nuclear Power Plants[J]. Nuclear Power Engineering, 2012, 33(1): 14-18.

[5] 陈俊. 基于变态模型的核电站新型安全壳地坑过滤器的研发[D]. 上海: 上海交通大学, 2015.

CHEN Jun. Design of a New Type of Rector Sump Strainer Based on Distorted Model[D]. Shanghai: Shanghai Jiao Tong University, 2015.

[6] 李石磊, 谢洪虎, 何英勇, 等. 安全壳地坑过滤器压损数值模拟与试验研究[J]. 核科学与工程, 2019, 39(6): 867-871.

LI Shi-lei, XIE Hong-hu, HE Ying-yong, et al. Simulation and Experimental Study on Head Loss of Containment Sump Strainer[J]. Nuclear Science and Engineering, 2019, 39(6): 867-871.

[7] 侯建飞, 王庆礼, 司恒远. 核电厂事故后安全壳内置换料水箱碎片传输性能分析[J]. 核动力工程, 2021, 42(5): 76-80.

HOU Jian-fei, WANG Qing-li, SI Heng-yuan. Analysis of Post-Accident Debris Transport Performance in In-Containment Refueling Water Storage Tank in Nuclear Power Plants[J]. Nuclear Power Engineering, 2021, 42(5): 76-80.

[8] 于肖宇. 核电站地坑过滤器附加质量的研究[D]. 上海: 上海交通大学, 2010.

YU Xiao-yu. Study of Added Mess the Containment Sump Strainer in Nuclear Plant[D]. Shanghai: Shanghai Jiao Tong University, 2010.

[9] 谢洪虎, 李石磊, 张峰, 等. 核电厂安全壳内置换料水箱过滤系统过滤性能及阻力特性研究[J]. 核动力工程, 2019, 40(6): 130-134.

XIE Hong-hu, LI Shi-lei, ZHANG Feng, et al. Assessment of Filtering and Pressure Drop Performances of IRWST Sump Strainers for Nuclear Power Plants[J]. Nuclear Power Engineering, 2019, 40(6): 130-134.

[10] SERTIĆ J, KOZAK D, SAMARDŽIĆ I. Calculation of Reaction Forces in the Boiler Supports Using the Method of Equivalent Stiffness of Membrane Wall[J]. The Scientific World Journal, 2014, 2014: 392048.

[11] 黄义仿, 贾汝民. 关于等效刚度法适用条件的讨论[J]. 力学与实践, 1996, 18(2): 59-60.

HUANG Yi-fang, JIA Ru-min. Discussion on the Applicable Conditions of Equivalent Stiffness Method[J]. Mechanics and Practice, 1996, 18(2): 59-60.

[12] 张煜, 包太, 秦永留. 加肋板在横向载荷和板中面力共同作用下的挠度分析[J]. 贵州大学学报(自然科学版), 2009, 26(1): 111-114.

ZHANG Yu, BAO Tai, QIN Yong-liu. Analysis of Deflection of Stiffened Plates with Rids under Transverse Load Together with the Neutral Plane Forces[J]. Journal of Guizhou University (Natural Science Edition), 2009, 26(1): 111-114.

[13] 丁婷, 丁圣果, 姜宇. 基于能量原理的肋型板等效刚度[J]. 西安建筑科技大学学报(自然科学版), 2013, 45(6): 858-863.

DING Ting, DING Sheng-guo, JIANG Yu. Equivalent Stiffness of Rib Board Based on the Energy Principle[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2013, 45(6): 858-863.

[14] 李绮文, 丁婷, 丁圣果. 计算肋形板自振频率的能量法[J]. 山西建筑, 2012, 38(26): 33-34.

LI Qi-wen, DING Ting, DING Sheng-guo. Energy Method of Calculating Natural Vibration Frequency of Rib Plate[J]. Shanxi Architecture, 2012, 38(26): 33-34.

[15] 孟维迎, 孙鹏文, 张兰挺, 等. 基于能量法的复合材料层合板性能等效算法研究与应用[J]. 太阳能学报, 2014, 35(8): 1505-1510.

MENG Wei-ying, SUN Peng-wen, ZHANG Lan-ting, et al. Research and Application of Property Equivalence Algorithm for Composite Lamination Plate Based on Energy Method[J]. Acta Energiae Solaris Sinica, 2014, 35(8): 1505-1510.

[16] 吴晓. 用改进能量法计算梁屈曲荷载和固有频率[J]. 工程与试验, 2019, 59(2): 1-3.

WU Xiao. Calculation of the Buckling Loads and Natural Frequency of Beams by Improved Energy Method[J]. Engineering & Test, 2019, 59(2): 1-3.

[17] 徐芝纶. 弹性力学(下)[M]. 北京: 高等教育出版社, 1980.

XU Zhi-lun. Elastic Mechanics (II)[M]. Beijing: Higher Education Press, 1980.

[18] 丁圣果. 分析结构力学[M]. 贵阳: 贵州科技出版社, 2010.

DING Sheng-guo. Mechanics of Analysis Structural[M]. Guiyang: Guizhou Science and Technology Publishing Press, 2010.

[19] 丁圣果, 刘广宁, 丁绮文. 肋型楼盖的一种有限元算法及其内力分布[J]. 建筑结构, 1999(6): 46-50.

DING Sheng-guo, LIU Guang-ning, LI Qi-wen. A Finite Element Method of Ribbed Floor System and Its Internal Distribution[J]. Building Structure, 1999(6): 46-50.

[20] 杨章, 童根树, 张磊. 对称布置2根单侧加劲肋的有效刚度[J]. 浙江大学学报(工学版), 2016, 50(8): 1446-1455.

YANG Zhang, TONG Gen-shu, ZHANG Lei. Effective Rigidity of Two One-Side Stiffeners Arranged Symmetrically[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(8): 1446-1455.

[21] BLEVINS R D. Formulas for natural frequency and mode shape[M]. New York: Van Nostrand Reinhold Co, 1979.

[22] 谢贻权, 何福保. 弹性和塑性力学中的有限单元法[M]. 北京: 机械工业出版社, 2000.

XIE Yi-quan, HE Fu-bao. Finite Element Method of Elasticity and Plastic Mechanics[M]. Beijing: China Machine Press, 2000.

[23] 陈学潮, 刘永仁, 金瑞椿. 加肋管板的变形和应力分析[J]. 上海力学, 1980, 1(3): 13-27.

CHEN Xue-chao, LIU Yong-ren, JIN Rui-chun. The Analysis of Deformations and Stresses of Ribbed Tube-Plate[J]. Chinese Quarterly of Mechanics, 1980, 1(3): 13-27.

[24] 钱浩, 邓晶晶, 徐定耿, 等. 安全壳再循环地坑滤网应力分析[J]. 力学季刊, 2007, 28(1): 165-169.

QIAN Hao, DENG Jing-jing, XU Ding-geng, et al. Stress Analysis of Recirculating Pit Filter in Containment[J]. Chinese Quarterly of Mechanics, 2007, 28(1): 165-169.

[25] 朱贺. 循环水浸泡影响下的新型地坑过滤器抗震分析[J]. 核安全, 2014, 13(4): 90-94.

ZHU He. Anti-Seismic Analysis on a New Type of Sump Filter in Circulating Water Immersion Condition[J]. Nuclear Safety, 2014, 13(4): 90-94.

Application of Stiffness Equivalent In Seismic Analysis of Containment Sump Filter Retention Basket

LAN Tian-bao, DONG Jiao-jiao, PENG Xing-ming, SHENG Feng

(China Nuclear Power Engineering Co., Ltd., Beijing 100840, China)

The work aims to calculate the stiffness equivalent of the filter plate of the containment sump filter retention basket.Energy method and anisotropy method were used to calculate the equivalent stiffness of the filter plate of the containment sump filter retention basket. The frequency obtained by the energy method based on equal deformation energy was much larger than the cutoff frequency of seismic response spectrum, which was suitable for the engineering requirements of the stranded basket model. There was a 14% difference between the principal frequency obtained by anisotropy method and that of the actual model. Both methods can meet the engineering requirements, and the anisotropic method is closer to the actual model. Finally, the model based on the energy method and the anisotropic stiffness equivalent filter plates has good results.

containment sump filter, retention basket, filter plate, equivalent, seismic analysis

2021-04-13；

2022-02-14

LAN Tian-bao (1990-), Male, Master.

盛锋（1980—），男。

Corresponding author：SHENG Feng (1980-), Male.

兰天宝, 董娇娇, 彭星铭, 等. 刚度等效在地坑过滤器滞留篮抗震分析中的应用[J]. 装备环境工程, 2023, 20(2): 096-101.

TL362

A

1672-9242(2023)02-0096-06

10.7643/ issn.1672-9242.2023.02.013

2021–04–13；

2022–02–14

兰天宝（1990—），男，硕士。

LAN Tian-bao, DONG Jiao-jiao, PENG Xing-ming, et al. Application of Stiffness Equivalent In Seismic Analysis of Containment Sump Filter Retention Basket[J]. Equipment Environmental Engineering, 2023, 20(2): 096-101.

责任编辑：刘世忠