高超声速导弹随机振动响应分析

晁征，蒋书波，张广明，王刚

高超声速导弹随机振动响应分析

晁征1，蒋书波1，张广明1，王刚2

（1.南京工业大学 电气工程与控制科学学院，南京 211816；2.中国航天科工集团第二研究院201所，北京 100048）

研究某高超声速导弹飞行过程中的振动状态，获得导弹在给定压力载荷下的振动响应特性。结合有限元分析、随机振动理论，利用三维软件构建导弹有限元模型，并在Ansys Workbench平台对其进行模态分析及谐响应分析。基于模态分析结果，对导弹进行随机振动响应试验，探究导弹在频域及力学上的振动响应特征。计算得出导弹前六阶固有频率和振型，获得导弹上一检测点在给定振动激励载荷下的加速度响应曲线，并得到导弹整体结构的应力分布云图。导弹模型强度符合要求，导弹在振动激励载荷下的加速度响应峰值均出现在380～400 Hz，应力极值出现在导弹尾部区域，在此区域内，导弹更易产生结构性损伤。在飞行器地面环境模拟试验中，应着重考虑此频域及位置的振动条件。

高超声速导弹；随机振动；脉动压力；模态分析；加速度响应；应力极值

高超声速导弹是指飞行速度大于5马赫，在大气层内以高于声速的速度飞行的航天飞行器，其速度快，具备高机动性，军事、民用价值巨大。高超声速导弹在大气层飞行时，所遭遇的振动环境非常严酷，当导弹壁面受到强大脉动载荷时，易致使导弹结构产生持续振动，产生的动态响应可能会导致导弹设备及机体结构的疲劳损坏。因此，对高超声速导弹所承受的脉动压力进行计算预示，并得出其响应分析结果是十分有必要的。导弹在高速飞行过程中，承受的压力载荷是一种典型的随机载荷，其在载荷激励下的动态响应可通过有限元软件计算得到。随着科学技术的发展，以及大型有限元软件的飞速进步，可以在大型有限元软件中建立导弹模型，并输入振动环境相关的载荷量，得到导弹在脉动压力激励下的随机振动响应[1-2]。

国内外已有大量学者对高超声速飞行器飞行过程中受到脉动压力载荷产生的动态响应进行了分析。蔡晓蕊等[3]给出了详细的脉动压力的估算方法。韩博文等[4]、蒋华兵等[5]将脉动压力载荷的空间相关性加入到动态响应分析中。张善智等[6]、李凰立等[7]利用数值方法对飞行器的结构振动响应和脉动气动载荷进行了计算。许茂等[8]在进行自由体结构脉动压力下的响应分析时，考虑了载荷之间的相关性问题。盖晓男等[9]提出了一种适用于锥–柱飞行器跨声速的脉动压力等效预示方法。郭静等[10]自主研发了气动力及脉动压力耦合分析软件，研究发现，气动弹性效应能够对结构耦合响应特性产生影响。范宣华等[11-12]为了形成自主再入飞行数值模拟预测技术，自主研发了PANDA 高性能力学分析平台，通过实验验证了相关功能的正确性。在此条件下，他们完成了一系列飞行器在脉动压力载荷下的随机振动分析算法，并使之运行。研究表明，飞行器再入过程的刚体运动对结构在低频段的响应影响显著，在中高频段，弹性响应逐渐占据主导地位。

上述文献就脉动压力载荷对飞行器结构响应进行了理论性的预测研究，探究出脉动压力载荷的普遍规律，以及飞行器的响应情况，已经为脉动压力环境预示研究打下了基础。但仿真的模型主体普遍是二维，并且高超声速飞行器在力学与频率上的响应特征并不十分清晰。本文通过文献查询及方法对比，采取随机振动功率谱密度法，在Solidworks三维设计软件中建立了细致的高超声速导弹模型，并在ANSYS软件中进行了一系列结构性的分析，输入相关载荷的功率谱密度曲线，即可得出导弹在频率与力学上的动态响应特征，为高超声速导弹的地面振动环境模拟试验及导弹机身强度设计提供了依据和参考。

1 高超声速导弹振动环境

高超声速导弹在飞行过程中，高速气流与边界层互相干扰，会产生严重的气动噪声[13]。伴随而来的脉动声压，易致使导弹结构产生非线性共振响应，造成导弹结构被破坏，极大地缩短了其使用寿命。

导弹产生脉动压力的途径大致可分为2类：其一为发动机的喷流效应；其二是导弹外壳壁面与空气来流产生的相互作用。查阅脉动压力相关文献[3]，可将脉动压力来源分为3种：附着湍流边界层，分离流和激波/边界层及波系的相互干扰区域[14-16]。附着湍流脉动压力具备一致的表现形式，其脉动压力的数学表达形式已经有了相对成熟的经验公式。后两者流场的形态极为复杂，暂没有成熟的数学模型来表示。

高超声速导弹在飞行过程中所受到的振动激励主要是由气动湍流引起的，其来流速度变化具有随机性，致使导弹在飞行过程中遭受严重的随机振动的考验，这对飞行器的航行精度以及飞行环境安全性有着非常重要的影响。高超声速导弹的随机振动地面模拟试验通常是在振动台上完成的，但考虑到振动台的控制精度以及夹具等其他要求限制，可在有限元仿真软件中完成随机振动仿真。由于根据脉动压力公式推演导弹所受激励载荷的功率谱密度过程较为复杂，现根据国军标及相关文献论述[17]，采用某型导弹挂飞试验振动试验的功率谱密度曲线[18]作为随机激励，对超声速飞行器进行随机振动响应分析。功率谱密度曲线如图1所示，1=0.005 22/Hz，2=0.082/Hz，1=500 Hz，2=1 500 Hz，1拐点处频率为30 Hz，总输入能量量级为11.62。

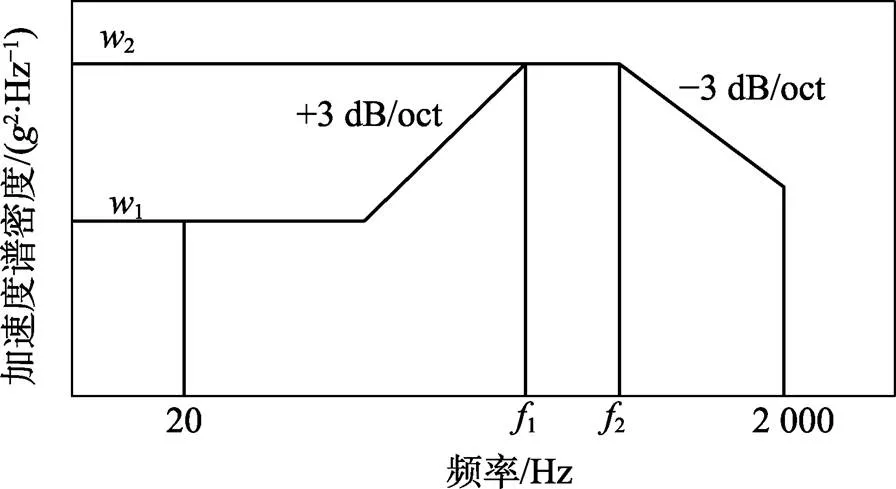
图1 某型导弹振动功率谱密度曲线

2 导弹有限元分析

有限元分析方法主要有前处理、分析求解、后处理三大步骤，其主要流程如图2所示。

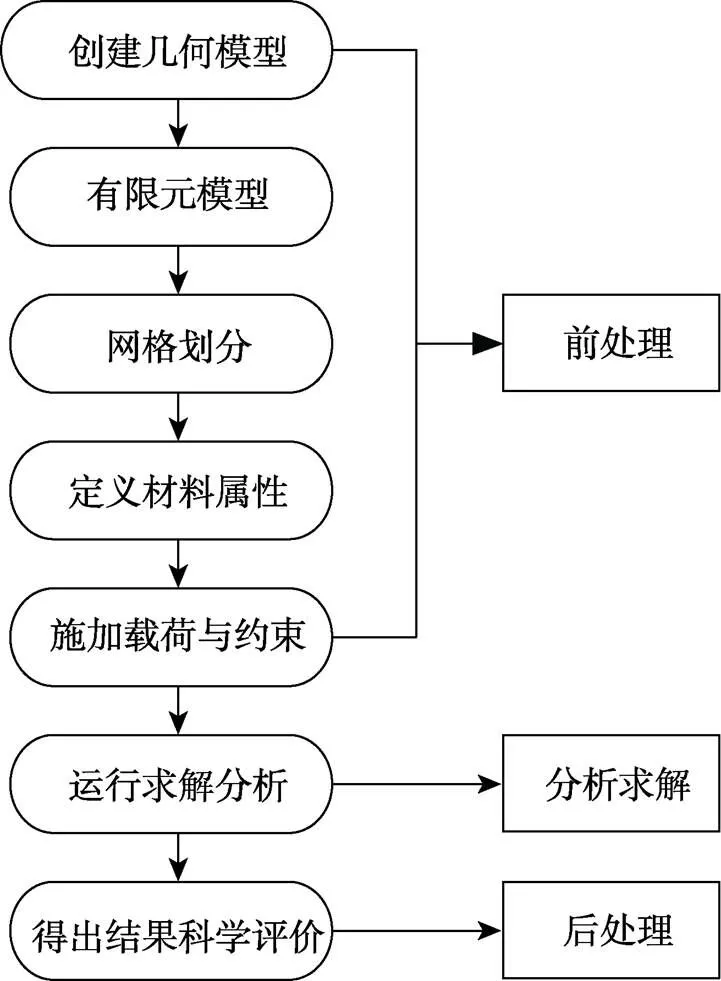
图2 有限元分析流程

2.1 导弹模型简化

有限元模型与有限元分析法相对应，它是一个只在节点处进行连接的单元组合体，也只能靠节点来传递力，且仅仅在节点处受到约束。有限元模型需与本文的分析内容和硬件性能相匹配[19]。简化模型不仅保障了计算的精确性，而且还有利于后续进行的网格划分。

1）删除细节。实际结构虽复杂，但有限元建模时可以将一些细节忽略删除，如果保留它们，会直接影响分析结果，出现应力集中。如删除构件的小孔、退刀槽等，用直角代替倒角圆角，去掉螺纹孔的螺纹，继而以圆孔代替。

2）装配体的简化。机械几何体的装配方法多种多样，例如螺栓连接和焊接等。当装配体的连接处所受的力很小，可以忽略时，就可以对其进行简化。如螺栓连接可以用节点的耦合来代替。对于本文的焊接装配体，可以将其焊接处当作一个整体来进行分析。

3）利用对称性。一部分结构相对于另外一部分结构在几何形状、支撑条件和力学性能等方面完全相同，这就是结构的对称性。当结构具有对称性时，只需对其结构的1/2进行分析即可，这也可以降低有限元模型的复杂程度，达到简化模型的目的。

在对整体系统进行三维建模后，剔除掉不必要的圆角和圆孔，对复杂曲面进行合并，最终得到的三维模型如图3所示。

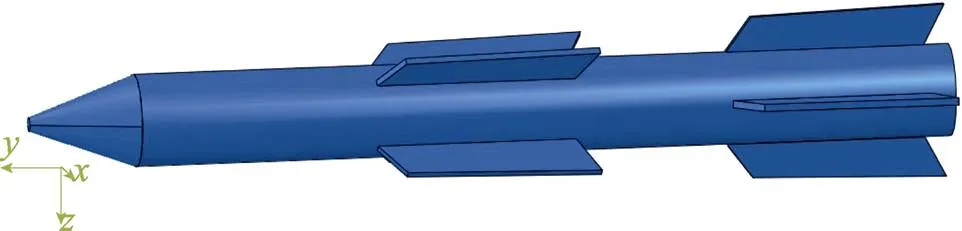
图3 某型导弹三维模型

2.2 导弹装置材料属性

经查询参考文献及导弹资料，导弹模型所用材料的属性参数见表1。

表1 某型导弹材料属性

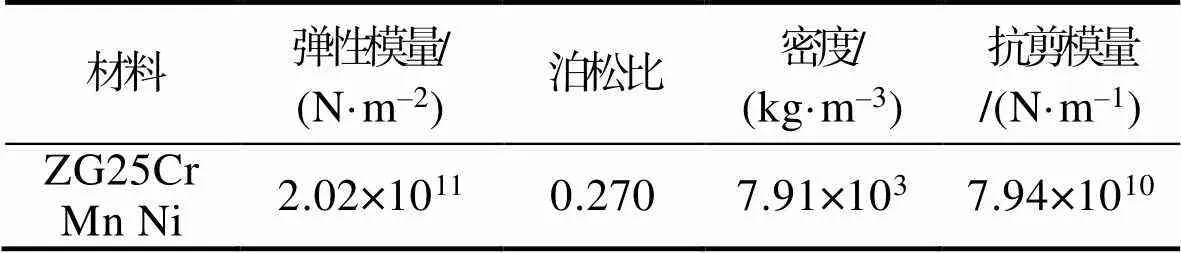
Tab.1 Material attribute of a certain missile

2.3 导弹装置网格划分

网格划分是有限元分析法中最重要的一个步骤，其对有限元数值分析结果的准确性有着至关重要的作用。由于划分网格是一个重要环节，下面对网格划分的基本原则进行简单介绍，以便合理、准确地建立有限元模型。

本文采用ANSYS软件进行网格划分，采用六面体及四面体十节点网格划分2种划分法。本项装置总共有22 110个单元，35 468个节点。模型划分结果如图4所示。由图4可知，导弹模型的网格整体质量在0.85～1，说明网格质量达标，符合要求。

图4 网格划分模型

3 导弹动力学分析

3.1 导弹模态分析原理

模态分析法通过计算结构的固有频率和振型，与激振频率相对比，频率相近的极易产生共振现象，从而找到结构上的薄弱点，对其作出改进[20]。现对高超声速导弹进行模态分析。

由机械振动理论可知，自由度无阻尼线性系统的运动方程为[21]：

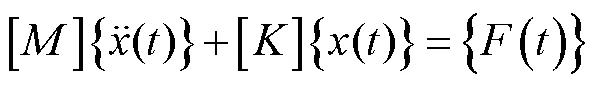
忽略外载荷的影响，则式（1）可以进一步化简为：

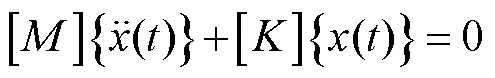
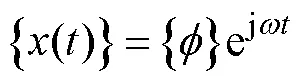
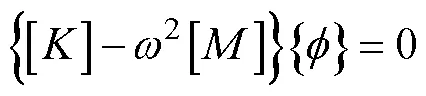
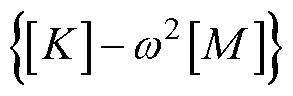
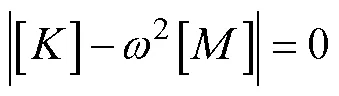
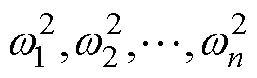
3.2 导弹模态结果分析

通过对导弹结构进行模态分析，可以掌握该结构在实际工况中的变形情况和相关变形量的大小，从而对提高结构稳定性发挥重要作用[22]。在软件中进行导弹的随机振动响应分析，是对地面随机振动试验的仿真，因此应对导弹施加约束。约束位置的选取会对导弹模态分析产生影响，现选取合适的壁面施加、、三个方向的位移约束。

导弹装置前6阶模态的振型如图5所示。从图5中可以看出，由于飞行器设计为锥柱体结构，其结构具有对称性，出现了对称振型。第一、二阶模态导弹机身出现轻微弯曲，变形量最大值出现在导弹头部位置。对于第三、四阶模态振型，机身弯曲程度加剧，最大变形量从头部位置延伸到机身。第五、六阶模态在三、四阶模态的基础上，出现了整个形体的扭转弯曲变形。此处振型并不是反映导弹真实的结构位移，而是以模态坐标的形式去反映振后变形的趋势[23]。在实际工作过程中，要避开导弹装置的模态频率，特别是一阶和二阶频率。

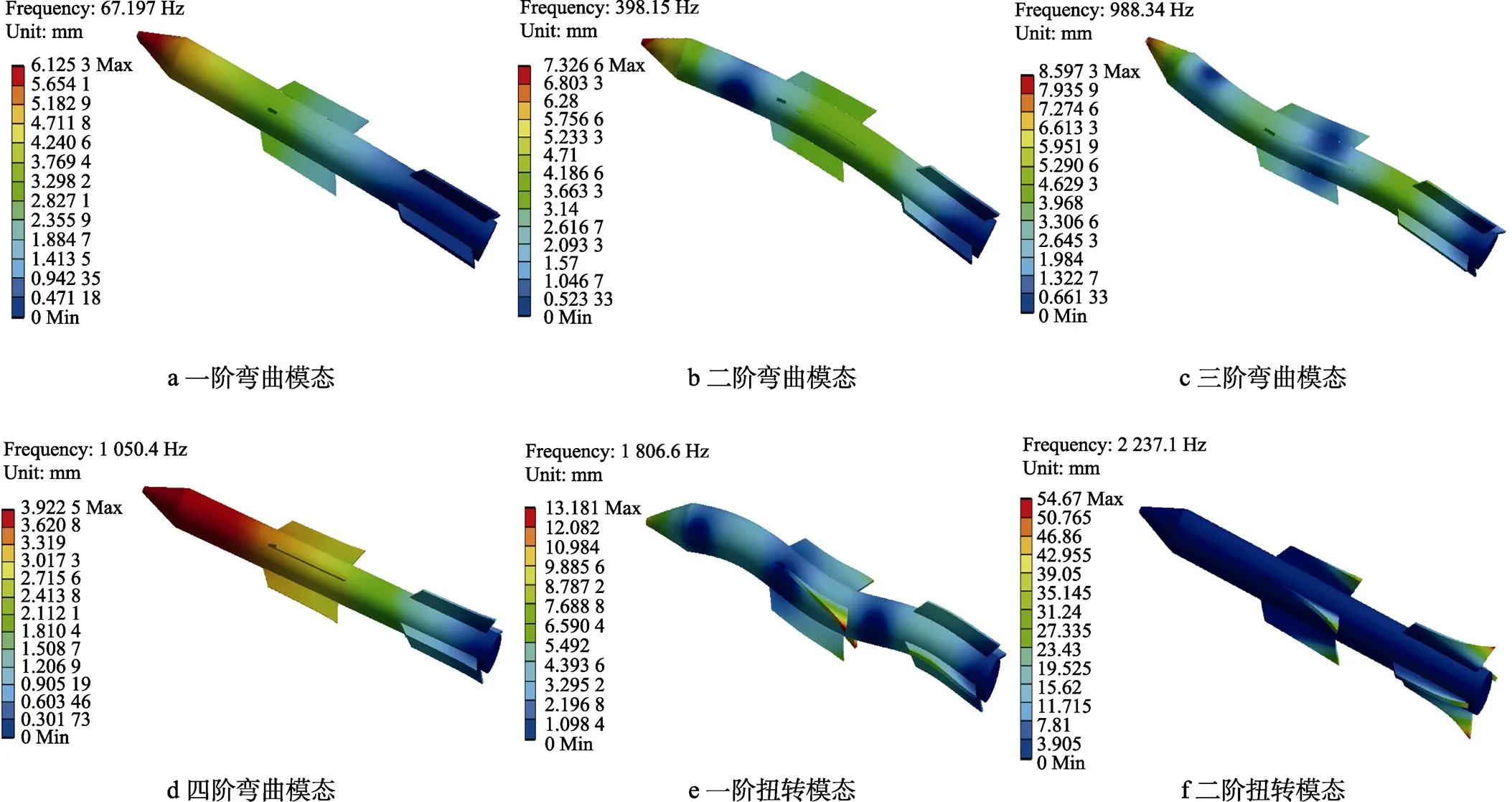
图5 导弹装置前六阶模态的振型

导弹装置的前6阶模态频率见表2。

表2 某型导弹前6阶模态频率

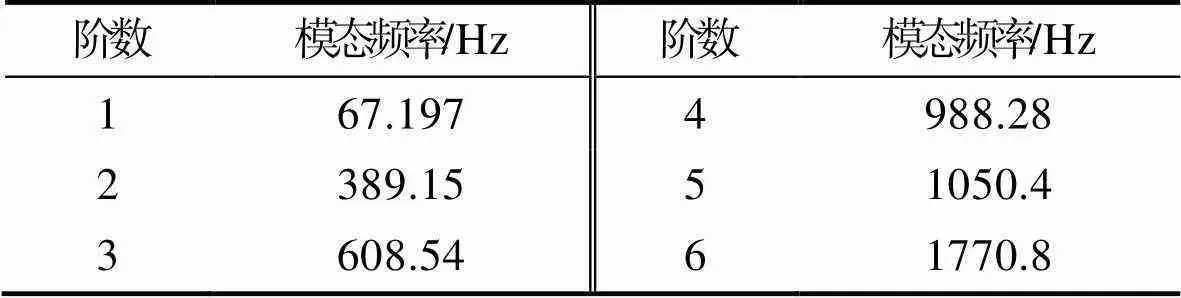
Tab.2 The first six modal frequencies of a missile

3.3 导弹装置谐响应分析

任何持续的周期性荷载，都会使装置结构产生持续的谐响应。谐响应分析是为了求解物体在受到周期载荷时的动态响应，可计算出结构系统在频域内的振动情况，并得到其振动的幅值曲线。高超声速导弹飞行时，由于长期受周期性载荷的作用，因此在对高声速导弹作模态分析的基础上，对导弹进行谐响应分析也是十分必要的[24]。谐响应分析通常采用3种方法进行：完全法、缩减法、模态叠加法。本次仿真中使用的是模态叠加法。

随着导弹激励载荷频率的上升，导弹振动过程中产生的应力值变化曲线如图6所示，其中Δ设置为195 Hz。从图6可知，应力值在振动频率245～830 Hz内逐渐增加，但数值变化很小。在830～1 025 Hz内，应力值随频率的增加而剧烈上升，当频率达到1 025 Hz时，达到峰值2.35 MPa。在1 025 Hz以后，幅值开始逐步衰减。因此分析可知，导弹受到载荷激励时，振动频率会对导弹的稳定性产生较大影响，当导弹振动频率达到1 025 Hz时，振动响应最为显著。结合模态分析结果可知，该频率是第五阶模态所对应的振动频率，所以导弹的第五阶模态是整个结构在谐响应载荷下振动的主振型，对振动的贡献量最大。

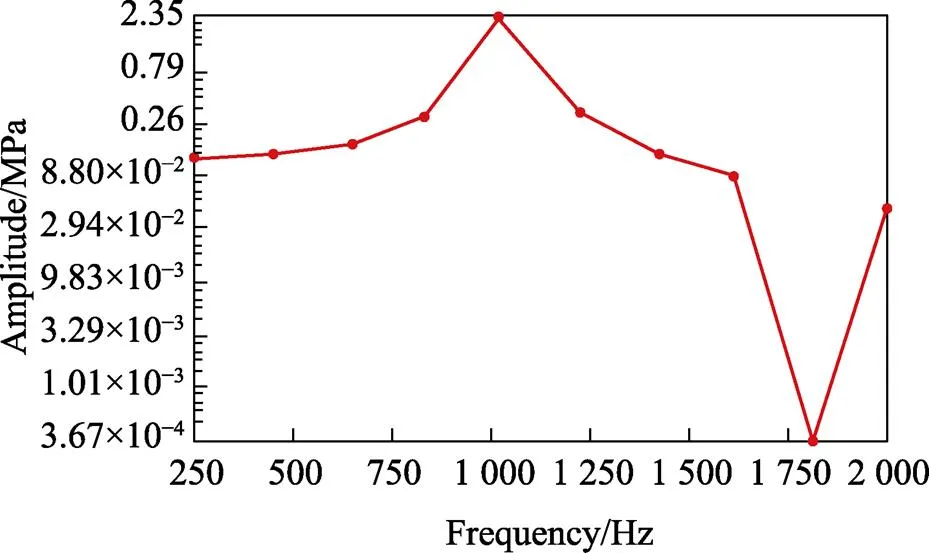
图6 导弹装置幅频响应曲线

4 导弹随机振动分析

随机振动的激励信号是随机波。导弹装置在工作过程中，同时存在各种可能的频率，某些频率比较复杂，存在很多不确定性，但该频率有可能对导弹系统比较薄弱的部位会产生破坏[25]。基于3.2小节所进行的模态分析，本节通过随机振动分析方法，采用载荷功率谱法分析计算导弹装置的整体响应曲线。

4.1 加速度响应

在模态分析以及谐响应分析的基础上，进行随机振动响应分析。按图1条件分别在、、方向对导弹输入加速度激励，导弹上的监测点在、、方向上的加速度响应如图7所示。由响应结果可知，3个方向的加速度响应均在380～400 Hz出现峰值。说明在此频率区间内，导弹的结构强度更易遭到破坏，甚至产生共振现象，是飞行器整体结构振动的危险点所在。因此，在导弹地面振动环境试验中，应尽量避免此区间内的振动频率，以免对装置产生结构性损伤。经比对模态分析所得固有振型，380～400 Hz内对应其第二阶模态，导弹开始产生显著变形，说明导弹在此区间经受比较严重的振动激励，二者分析的结果相符。

4.2 应力云图

导弹受、、方向随机振动试验的应力响应如图8所示。由应力云图可以看出，导弹受到振动载荷，产生应力的最大值集中在导弹尾部位置，3最大值可达到388.75 MPa。最大值远低于导弹材料所能承受极限强度，因此在应力强度方面可满足要求。由分析结果可推断，高声速导弹在飞行过程中，其尾部位置更易受到压力载荷的作用，产生结构上的疲劳和损伤，为导弹的危险部位。在进行导弹结构设计及地面振动模拟试验时，也应着重考虑飞行器尾部位置的振动强度。

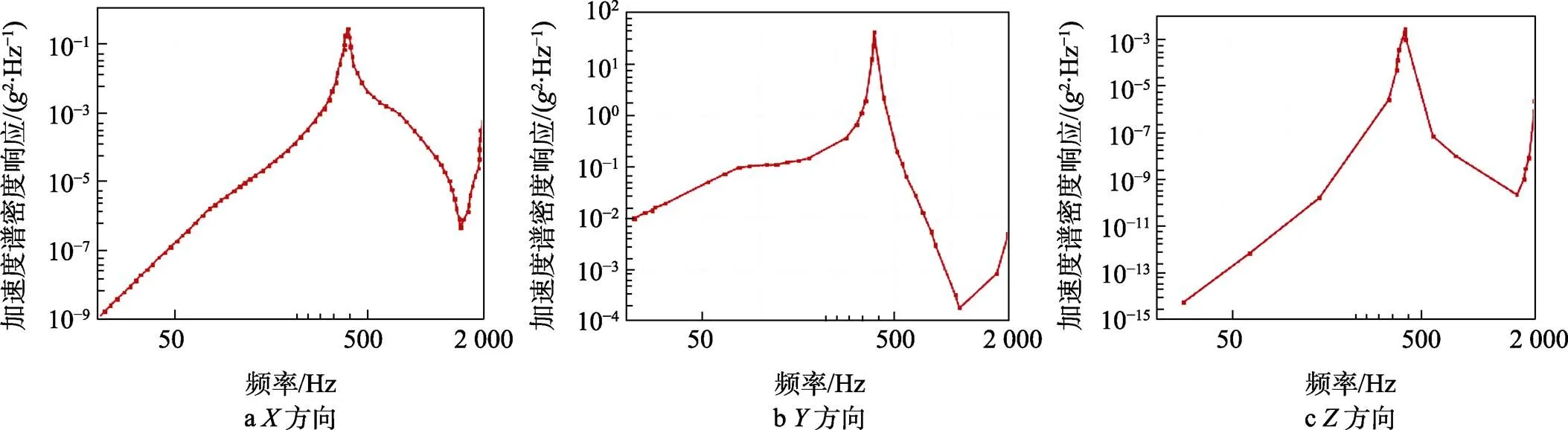
图7 振动加速度响应

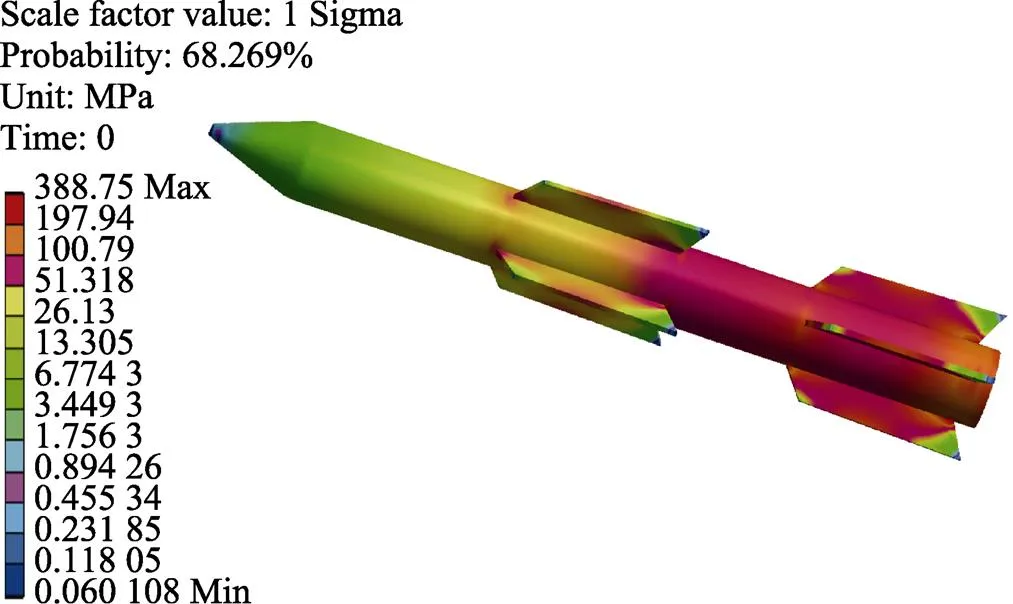
图8 导弹应力分布云图

5 结语

针对某型号高超声速导弹整体结构，依据国家相关标准，选取某挂飞试验振动实测数据的功率谱密度曲线作为随机激励谱，进行了多软件联合仿真，对导弹进行了模态分析及谐响应分析。最后在给定激励条件下进行了随机振动试验，得出三维导弹模型在频域与力学上的响应特征。

本文给导弹结构设计以及地面环境模拟试验提供了一定参考依据。由于载荷输入采用的是某型导弹挂飞试验振动试验的功率谱密度曲线，并不能代表脉动压力环境对高超声速导弹造成的整体载荷量，且脉动压力下高超声速飞行器的响应频带很宽，甚至可以达到10 kHz，因此在随机振动试验的振动激励以及高频响应方面，还需进一步的研究与分析。

[1] SAHOO R, GROVER N, SINGH B N. Random Vibration Response of Composite–Sandwich Laminates[J]. Archive of Applied Mechanics, 2021, 91(9): 3755-3771.

[2] 袁名松, 冯建伟, 黄云, 等. 巡飞攻击导弹红外成像导引头随机振动响应分析[J]. 红外技术, 2015, 37(4): 342-346.

YUAN Ming-song, FENG Jian-wei, HUANG Yun, et al. Random Vibration Response Analysis of Loitering Attack Missile Imaging Infrared Seeker[J]. Infrared Technology, 2015, 37(4): 342-346.

[3] 蔡晓蕊. 高超声速脉动压力的计算方法研究[D]. 南京: 南京航空航天大学, 2019.

CAI Xiao-rui. Research on Calculation Method Of Hypersonic Pulsating Pressure[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019.

[4] 韩博文, 冷小磊. 脉动噪声环境下飞行器结构的响应分析[J]. 江苏航空, 2012(S1): 35-37.

HAN Bo-wen, LENG Xiao-lei. Response Analysis of Aircraft Structure in Pulsating Noise Environment[J]. Jiangsu Aviation, 2012(S1): 35-37.

[5] 蒋华兵, 李春丽, 陈强洪. 再入飞行器脉动压力环境特性分析[J]. 航天器环境工程, 2010, 27(3): 378-382.

JIANG Hua-bing, LI Chun-li, CHEN Qiang-hong. The Characteristics of the Fluctuating Pressure Environment for a re-Entry Vehicle[J]. Spacecraft Environment Engineering, 2010, 27(3): 378-382.

[6] 张善智, 闫云聚, 崔盼礼. 高速飞行器结构与气流耦合振动特性研究[J]. 机械强度, 2010, 32(1): 21-24.

ZHANG Shan-zhi, YAN Yun-ju, CUI Pan-li. Research on Interaction Characteristic between Flying Missile Structure and high-Speed Airflow[J]. Journal of Mechanical Strength, 2010, 32(1): 21-24.

[7] 李凰立, 苏虹, 沈丹, 等. 飞行器脉动压力的CAA方法研究[J]. 强度与环境, 2019, 46(2): 13-20.

LI Huang-li, SU Hong, SHEN Dan, et al. Fluctuating Pressure Simulation of Aircraft Based on Computational Aeroacoustics[J]. Structure & Environment Engineering, 2019, 46(2): 13-20.

[8] 许茂, 李上明, 吴连军. 考虑脉动压力相关性的自由体随机振动分析[J]. 装备环境工程, 2021, 18(3): 29-33.

XU Mao, LI Shang-ming, WU Lian-jun. Random Vibration Analysis of Free Body under Fluctuating Pressure Considering Correlation[J]. Equipment Environmental Engineering, 2021, 18(3): 29-33.

[9] 盖晓男, 于开平. 飞行器跨声速段肩部脉动压力等效预示方法[J]. 噪声与振动控制, 2020, 40(1): 1-4.

GAI Xiao-nan, YU Kai-ping. An Equivalent Prediction Method for Shoulder Pulsating Pressure of Flight Vehicle in Transonic Phase[J]. Noise and Vibration Control, 2020, 40(1): 1-4.

[10] 郭静, 张忠, 谷迎松, 等. 空气舵气动力-脉动压力-结构耦合响应分析[J]. 航天器环境工程, 2020, 37(3): 235-239.

GUO Jing, ZHANG Zhong, GU Ying-song, et al. Analysis of Aerodynamic Force-Fluctuating Pressure-Structure Coupled Response for Air Rudder[J]. Spacecraft Environment Engineering, 2020, 37(3): 235-239.

[11] 王柯颖, 胡杰, 范宣华, 等. 基于PANDA平台的飞行器脉动压力激励随机振动响应分析[J]. 装备环境工程, 2021, 18(3): 38-44.

WANG Ke-ying, HU Jie, FAN Xuan-hua, et al. Random Vibration Response Analysis of Aircraft with Pulsating Pressure Excitation Based on PANDA Platform[J]. Equipment Environmental Engineering, 2021, 18(3): 38-44.

[12] 范宣华, 王柯颖, 肖世富, 等. 强脉动压力下飞行器随机振动分析算法与并行实现[J]. 计算物理, 2021, 38(2): 192-198.

FAN Xuan-hua, WANG Ke-ying, XIAO Shi-fu, et al. Algorithm for Multi-Point Random Vibration Analysis of a Flight Device under Strong Fluctuating Pressures and Parallel Implementation[J]. Chinese Journal of Computational Physics, 2021, 38(2): 192-198.

[13] 黄寿康. 流体动力·弹道·载荷·环境[M]. 北京: 宇航出版社, 1991: 65-81.

HUANG Shou-kang. Fluid Power, Trajectory, Load and Environment[M]. Beijing: Aerospace Publishing House, 1991: 65-81

[14] ROBERTSON J E. Prediction of In-Flight Fluctuating Pressure Environments[J]. The Journal of the Acoustical Society of America, 1971, 50(1A): 120-121.

[15] 陈伟芳, 张志成, 石于中, 等. 再入体表面脉动压力环境的预测[J]. 国防科技大学学报, 2001, 23(6): 20-23.

CHEN Wei-fang, ZHANG Zhi-cheng, SHI Yu-zhong, et al. The Prediction of Fluctuating Pressure on the Surface of Reentry Vehicles[J]. Journal of National University of Defense Technology, 2001, 23(6): 20-23.

[16] LAGANELLI A L, WOLFE H F. Prediction of Fluctuating Pressure in Attached and Separated Turbulent Boundary-Layer Flow[J]. Journal of Aircraft, 1993, 30(6): 962- 970.

[17] GJB 150.16A—2009, 军用装备实验室环境试验方法.第16部分: 振动试验[S].

GJB 150.16A—2009, Environmental Test Methods for Military Equipment[S].

[18] 赵青, 吴瑞轩. 空空导弹新研元器件振动试验条件探讨[J]. 装备环境工程, 2020, 17(8): 115-118.

ZHAO Qing, WU Rui-xuan. Analysis of Vibration Test Condition of New Developed Components of Air-to-Air Missle[J]. Equipment Environmental Engineering, 2020, 17(8): 115-118.

[19] 吕金洲. 飞行器模型结构动力学及性能研究[D]. 成都: 西南交通大学, 2015.

LYU Jin-zhou. Research on Structural Dynamics and Performance for Aircraft Model[D]. Chengdu: Southwest Jiaotong University, 2015.

[20] 孙海文, 胥磊. 某火箭模态分析与模态试验[J]. 兵器装备工程学报, 2017, 38(6): 176-179.

SUN Hai-wen, XU Lei. Modal Analysis and Modal Test of a Rocket[J]. Journal of Ordnance Equipment Engineering, 2017, 38(6): 176-179.

[21] 张宏. 深海钻井用高压泥浆泵轻量化设计研究[D]. 兰州: 兰州理工大学, 2018.

ZHANG Hong. The Research on Lightweight Design of High Pressure Slurry Pump Used in Deep Sea Drilling[D]. Lanzhou: Lanzhou University of Technology, 2018.

[22] 杜振宇, 王学智, 李康, 等. 防空导弹起落架结构振动特性仿真分析[J]. 导弹与航天运载技术, 2017(5): 84-88.

DU Zhen-yu, WANG Xue-zhi, LI Kang, et al. Simulation Analysis on Vibration Characteristics of Landing Gear of Air Defence Missile[J]. Missiles and Space Vehicles, 2017(5): 84-88.

[23] 王胜超, 杜颖, 王鹏飞, 等. 扑翼飞行器测力平台设计与振动特性仿真分析[J]. 计测技术, 2017, 37(5): 16-19.

WANG Sheng-chao, DU Ying, WANG Peng-fei, et al. Design and Vibration Characteristics Analysis of Force Measuring Platform of Flapping Wing Aircraft[J]. Metrology & Measurement Technology, 2017, 37(5): 16-19.

[24] 刘进进, 尹明德, 张志龙. 基于ANSYS的某直升机尾梁管模态及谐响应分析[J]. 机械工程与自动化, 2013(1): 64-66.

LIU Jin-jin, YIN Ming-de, ZHANG Zhi-long. Modal and Harmonic Analysis Based on ANSYS for Light Helicopter Tail Beam Tube[J]. Mechanical Engineering & Automation, 2013(1): 64-66.

[25] 段飞飞, 王田宇, 温业堃, 等. 飞行器随机振动试验技术应用研究[J]. 电子产品可靠性与环境试验, 2022, 40(2): 56-59.

DUAN Fei-fei, WANG Tian-yu, WEN Ye-kun, et al. Research on the Application of Random Vibration Test Technology of Aircraft[J]. Electronic Product Reliability and Environmental Testing, 2022, 40(2): 56-59.

Random Vibration Response of Hypersonic Missile

CHAO Zheng1, JIANG Shu-bo1, ZHANG Guang-ming1, WANG Gang2

(1. College of Electrical Engineering and Control Science, Nanjing Tech University, Nanjing 211826, China; 2. 201 Institute of the Second Research Institute of China Aerospace Science and Industry Corporation, Beijing 100048, China)

The work aims to study the vibration state of a hypersonic missile during flight and obtain the vibration response characteristics of the missile under a given pressure load. Combined with finite element analysis and random vibration theory, the finite element model of the missile was constructed with the three-dimensional software, and the modal analysis and harmonic response analysis were carried out on the platform of Ansys Workbench. Based on the modal analysis results, the random vibration response test of the missile was carried out to explore the vibration response characteristics of the missile in frequency domain and mechanics. The first six natural frequencies and vibration modes of the missile were calculated. The acceleration response curve of a detection point on the missile under a given vibration excitation load was obtained. The stress distribution pattern of the overall structure of the missile was obtained. The strength of the missile model meets the requirements. The peak acceleration response of the missile under vibration excitation load appears between 380 Hz and 400 Hz, and the extreme stress appears in the tail area of the missile. In this area, the missile is more prone to structural damage. In the ground environment simulation experiment of the missile, the vibration conditions in this frequency domain and position should be emphatically considered.

hypersonic missile; random vibration; fluctuation pressure; modal analysis; acceleration response; extreme stress

2022-05-19；

2022-07-01

CHAO Zheng (1994-), Male, Postgraduate.

蒋书波（1975—），女，博士，副教授，主要研究方向为工业过程检测。

Corresponding author：JIANG Shu-bo (1975-), Female, Doctor, Associate professor, Research focus: industrial process detection.

晁征, 蒋书波, 张广明, 等. 高超声速导弹随机振动响应分析[J]. 装备环境工程, 2023, 20(2): 050-056.

TJ760

A

1672-9242(2023)02-0050-07

10.7643/ issn.1672-9242.2023.02.007

2022–05–19；

2022–07–01

晁征（1994—），男，硕士研究生。

CHAO Zheng, JIANG Shu-bo, ZHANG Guang-ming, et al.Random Vibration Response of Hypersonic Missile[J]. Equipment Environmental Engineering, 2023, 20(2): 050-056.

责任编辑：刘世忠