深海压力–流速耦合环境下基于灰色系统理论的有机涂层寿命预测研究

陈宇凡，孟凡帝，刘莉，崔宇，刘叡，王福会

船舶及海洋工程装备

深海压力–流速耦合环境下基于灰色系统理论的有机涂层寿命预测研究

陈宇凡1，孟凡帝1，刘莉1，崔宇2，刘叡1，王福会1

（1. 沈阳材料科学国家研究中心 东北大学联合研究分部，沈阳 110819；2. 中国科学院金属研究所 师昌绪先进材料创新中心，沈阳 110016）

建立深海压力–流速耦合环境下有机涂层的寿命预测模型，并预测有机涂层在该环境下的服役寿命。首先针对涂层的湿态附着力变化结果，基于灰色系统理论，建立湿态附着力的GM(1,1)模型。随后再基于耦合环境下的试验结果，建立涂层水传输的扩散模型。最后，在此基础上，利用灰色关联分析方法，计算这2种失效影响因素在涂层失效过程中所占的权重因子，并基于这2个影响因素建立涂层失效的数学模型。经过数学统计验证和试验结果对比验证，该模型精度良好，可靠性高。该模型能够对深海压力–流速耦合环境下有机涂层的寿命进行准确预测。

深海压力–流速耦合环境；有机涂层；灰色系统理论；湿态附着力；水传输；寿命预测

在金属表面涂覆有机涂层是一种经济有效的防护手段[1-3]。因此，涂层的寿命预测对涂层的维护和性能评价具有现实的指导意义。然而，由于涂层失效机制的复杂性，寿命预测一直是涂层研究领域的一项艰巨任务[4-5]。对于服役于不同环境下的有机涂层，目前并没有发展出普适的寿命预测模型。Doherty等[6]建立了涂层起泡面积的数学模型，提出涂层的寿命可由涂层起泡的临界面积来确定。Maitland等[7]提出了基于聚合物薄膜电解电阻的预测公式。Bierwagen等[8]将电化学阻抗谱（EIS）数据分别与有机涂层在盐雾环境下的服役时间和涂层吸水率数据进行关联分析，提出了一种基于EIS相关数据预测涂层服役寿命的方法。Nguyen等[9]则根据实际工况构建了涂层吸水率与时间的关系模型，并利用该模型成功对有机涂层进行了寿命预测。Shevchuk等[10]介绍了基于涂层系统的物理化学和电化学过程的预测模型。一般来说，一个好的寿命预测模型应该基于服役条件下明确的失效机制，其试验条件符合实际工况条件，且模型预测结果与试验结果相符。然而，大多数提出的预测方法都没有考虑到以上所有的条件，这会使预测模型在使用的过程中存在局限性。

在深海环境中，因设备服役的实际工况不同，使得有机涂层失效的主导因素也有所不同。在前期的工作中，笔者课题组就不同的模拟深海环境下有机涂层的失效机制进行了研究。Liu等[11-13]通过研究常压和静水压力条件下有机涂层的失效行为，发现静水压力加速了有机涂层的失效，腐蚀介质在界面快速聚集，从而引起涂层湿态附着力的丧失，进而导致涂层的失效破坏。Tian等[14]、Liu等[15]、曹京宜等[16]通过研究在交变压力条件下有机涂层的失效行为，发现交变压力会对有机涂层产生的一种“推–拉作用”，致使涂层发生鼓泡开裂，从而导致涂层失效破坏。除了压力之外，设备与海水的相对运动所产生的流速也成为了环境中一个不可忽略的影响因素。有机涂层实际上是在深海压力–流速的耦合环境下服役。高浩东等[17]通过研究深海压力–流速环境下环氧玻璃鳞片涂层的失效行为，发现压力和流速作为单一环境变量均会加速涂层的失效，二者耦合表现出协同作用，进一步加速了涂层的失效破坏。Meng等[18]进一步研究发现，在耦合环境作用下，流体流动为水提供了初始动能，静水压力降低了吸水的能垒，且在流速和压力的协同作用下，涂层缺陷处内应力的释放，导致聚合物片从涂层表面脱离和造成大面积起泡。根据之前的研究结果发现，涂层/金属体系如果在涂层/金属界面处被破坏，其他保护机制将变得毫无价值。有机涂层的失效破坏受到许多不确定因素的影响，包括水的传输、界面附着力的变化、界面电化学反应、界面应力状态等。这些因素可能存在的相互作用，使有机涂层的失效破坏变得更加复杂。

灰色系统理论由邓聚龙在1982年创立，并在经济、气象、工程等多个领域得到了广泛的应用[19-22]。数学建模的研究还涉及其他现代数学方法，例如“黑盒”方法[23]、模糊系统理论[24]和人工神经网络[25]。在运用这些方法时，往往需要大量的数据结果用于训练和验证，才能保证其数学模型的准确性，而在有机涂层的失效过程中，通过试验监测得到的数据比较有限，并不能提供大量的数据用于训练和验证。灰色系统理论则可以有效地规避这一点，其对于有限的数据能够给出准确的计算结果，所以应选灰色系统理论来建立数学模型。耿刚强等[26]将该理论运用到了钢桥防腐蚀涂层的寿命预测研究中，提出了合理的寿命预测模型。李瑞超[27]和周立建等[28]将灰色系统理论与人工神经网络相结合，利用灰色预测所需样本量少、方法简单的优点和神经网络非线性映射能力强、并行处理能力突出的特点，对有机涂层的使用寿命进行了预测。Meng等[29]利用灰色系统理论研究了静水压力下有机涂层湿态附着力与涂层寿命的关系，将有机涂层的失效过程与涂层的湿态附着力联系起来，提出了一种合理的寿命预测模型。

目前的文献对深海环境下有机涂层的寿命预测工作报道较少，深海压力–流速耦合环境下有机涂层的寿命预测更是还未见文献报道。因此，本试验基于涂层湿态附着力测试以及涂层吸水率结果，并结合涂层EIS测试结果，利用灰色系统理论，建立了深海压力–流速耦合环境下有机涂层的寿命预测模型。这对进一步探索深海复杂海洋环境下有机涂层失效行为的评价方法，以及新型涂层的研发具有重要意义。

1 试验

本次试验中所采用的涂层体系为环氧–云母涂层体系，其成膜物质为E-44双酚A型环氧树脂（南通星辰合成材料有限公司），固化剂为低分子TY-650聚酰胺（沈阳正泰防腐材料有限公司），稀释剂为二甲苯（国药化学试剂集团有限公司）与正丁醇（国药化学试剂集团有限公司）的混合溶剂，其质量比为7︰3。颜填料为云母粉（上海麦克林生化科技有限公司），其目数为400目。树脂、固化剂、填料以及溶剂的质量比为1︰0.8︰0.36︰0.3。该涂层体系的制备过程为：按上述比例先将环氧树脂与混合溶剂混合，在磁力搅拌器上以150 r/min的转速搅拌0.5 h；搅拌均匀后，按上述配比加入400目云母粉继续搅拌0.5 h，使得云母粉充分溶解；之后按上述比例加入低分子TY-650聚酰胺搅拌0.5 h；然后，在25 ℃、RH为30%的环境中放置0.5 h，使其充分熟化；熟化后，对其进行10 min超声处理，以去除涂层中的气泡；超声处理后，将其取出，等待后续涂刷。

试验中所用的试样为自由膜和涂层/金属试样，其中自由膜试样涂覆在硅胶板上，固化后，将其裁剪成尺寸为75 mm×10 mm的长方形试样，用于涂层吸水率测试，膜层厚度为(400±10) μm。涂层/金属试样所用的基体金属为Q235钢，尺寸为40 mm×15 mm× 2 mm。打磨前均采用环氧树脂进行封装，其中用作电化学测试的试样需在钢片表面焊接铜导线。涂刷前，需将封装后的基体金属用水磨砂纸打磨至240#。涂刷完成后，需经25 ℃固化10 h、40 ℃固化2 h、60 ℃固化24 h后使用。膜层厚度为(200±10) μm。

利用模拟深海试验装置开展压力–流速耦合环境条件（6 MPa，3 m/s）下的试验[18]。该试验装置采用3.5%NaCl水溶液模拟海水环境，通过气体增压来控制服役环境的压力，利用搅拌电机驱动装置内的旋转笼，进而实现设备与服役环境相对运动速度的控制。试验装置如图1所示。

图1 模拟深海试验装置[18]

采用美国Delesko公司生产的PositestAT-A全自动拉拔式附着力检测仪对浸泡前的附着力试样，以及在深海压力–流速耦合环境下服役后的湿态附着力试样，按照ASTM D4541—02进行拉拔法附着力测试，每组试验取5个平行样，试验结果取其平均值。采用精密电子天平（BSA124S，精确度为0.000 1 g）测量涂层浸泡不同时间后的质量，通过涂层的质量变化测算出涂层的吸水率变化，吸水率计算公式为：

式中：Q为涂层在时刻点时的吸水率；m为涂层时刻点时对应的质量；0为涂层的初始质量。为保证试验的精确性，每组试验取5个平行样吸水率的平均值。

涂层/金属试样的电化学EIS测试是借助电化学工作站（PARSTAT 4000A）来完成的。测试采用三电极体系，测试频率为105～10-2Hz，电解池溶液为3.5%的NaCl水溶液，工作电极为待测涂层/金属试样，参比电极为饱和甘汞电极（SCE），对电极采用40 mm× 15 mm的Pt片。试验过程中，为了同涂层阻抗匹配，保证测试结果的准确性，对工作电极所加载的正弦扰动为60 mV。EIS测试结束后，使用ZSimpWin软件对所得到的数据进行拟合分析。

2 腐蚀机理及腐蚀预测

2.1 涂层湿态附着力GM(1,1)模型构建

环氧–云母涂层在深海压力–流速耦合环境下服役的附着力变化情况如图2所示。由图2可知，在深海压力–流速耦合环境条件下，其附着力均随着服役时间的增加而下降，呈非线性的变化规律。涂层的附着力丧失迅速，在72 h内从7.20 MPa下降到了2.44 MPa。结合涂层服役后的宏观形貌（如图3所示）以及涂层发生断裂时的断口形貌（如图4所示）可以看出，服役72 h后，深海压力–流速耦合环境下的涂层出现大面积的起泡，涂层遭到严重破坏，涂层/金属界面处完全断裂。这说明深海压力–流速耦合环境条件加速了涂层湿态附着力的下降，加剧了涂层的失效破坏。

图2 深海压力–流速耦合环境下涂层的附着力随时间的变化

图3 在深海压力–流速耦合环境下服役不同时间后涂层/金属样品的表面宏观形貌

图4 在深海压力–流速耦合环境下服役不同时间后涂层/金属样品的断口宏观形貌

由上述分析可知，在深海压力–流速耦合环境下，涂层的湿态附着力在短时间内迅速丧失。这个过程是一个极其复杂的过程，其影响因素很多，包括环境变量、界面处的电化学行为以及涂层应力释放等。这些因素虽然作用机制不明确，但最终都将导致涂层的湿态附着力数值下降。由于涂层所处的环境严苛，所得的数据有限，因此选用灰色系统理论来建立涂层湿态附着力变化情况的数学模型最为合适。

灰色系统理论的建模要求原始数据必须等时间间距。首先对原始数据进行累加生成，目的是弱化原始时间序列数据的随机因素；然后建立生成数的微分方程GM(,)，是微分方程的阶数，是参量的个数。其中，GM(1,1)模型，即单序列一阶灰色微分方程，由于其所需原始信息少，计算方法简便，模型精度高，是目前最常用的灰色模型。

涂层湿态附着力随浸泡时间变化的原始序列为(0)，(0)数列的一次累加数列为：

定义(1)数列的平均数列(1)为：

灰色微分方程GM(1,1)的最小二乘预测序列为：

(1)(k)的白化式微分方程为：

其中，参数和可由最小二乘法确定：

根据式（5），(1)(k)在时刻的解为：

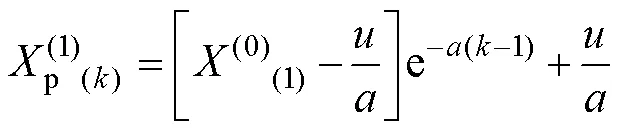
式中：代表预测值。进而得到还原数列(0)(k)在时刻的解为：

由于：

用替换，并代入式（7）可得：

式中：1为时间序列的初始时间，初始时间为0；是时间间隔，取12 h；和的值分别为0.149 3和6.975 6。拟合结果如图5所示。可以看出，模型值和实测值符合得较好，说明GM(1,1)模型能够正确地反映深海压力–流速耦合环境下涂层湿态附着力随浸泡时间的变化规律。

图5 深海压力–流速耦合环境下涂层湿态附着力GM(1,1)模型的拟合结果

为了分析该模型的精度，对其相对误差（RE）和平均相对误差（ARE）进行了计算分析，结果见表1。相对误差和平均相对误差的计算公式为：

从表1可以看出，对于深海压力–流速耦合环境，其GM(1,1)模型每个时间点的相对误差在±12%以内，其平均相对误差为6.65%。对浸泡96、120 h的湿态附着力进行预测后，其相对误差也在±12%以内，平均预测误差为8.05%。可见，所建立的GM(1,1)模型其整体精度较好，能正确地反映深海压力–流速耦合环境下涂层湿态附着力随浸泡时间的变化规律，具有良好的可靠性。

表1 湿态附着力的GM(1,1)模型与实测数据的相对误差分析

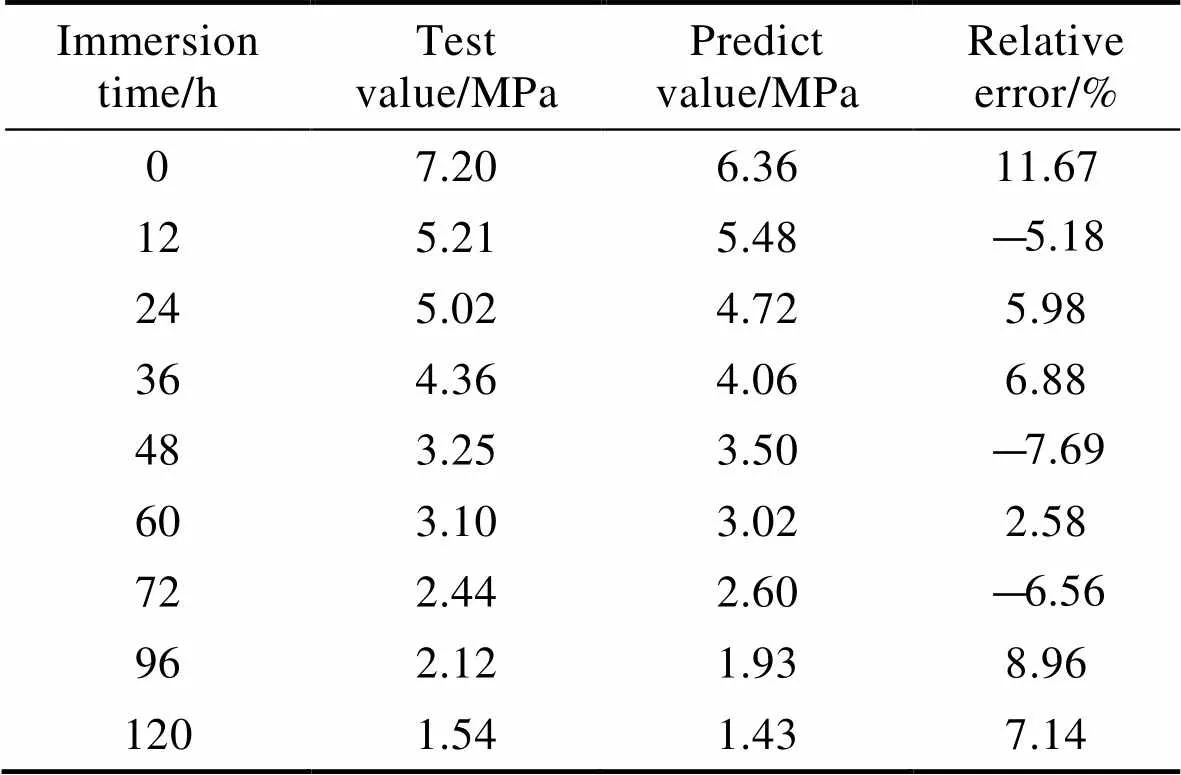
Tab.1 Relative error analysis between the GM(1,1) model and the measured data of wet adhesion

2.2 涂层的水传输模型构建

涂层中水等腐蚀介质的传输是导致涂层失效破坏的因素之一。涂层的吸水动力学可以反映涂层内部缺陷的变化情况，以及表征涂层的抗渗透能力，是评价涂层失效破坏的重要参数。在深海压力–流速耦合环境下，环氧–云母涂层的吸水率随时间的变化曲线如图6所示。从图6中可以看出，涂层吸水率的变化经历了明显的2个阶段。在初始时刻至96 h这段时间内，吸水率随着时间的增长而上升，上升速度逐渐减慢；在96～240 h这段时间内，吸水率随时间的增长变化幅度不大，且逐渐趋于稳定，饱和吸水率为2.06%。

图6 深海压力–流速耦合环境下涂层吸水率随服役时间的变化曲线

根据Tian等[14]的研究表明，当涂层的吸水率小于饱和吸水率的60%时，即本试验中0～24 h这段时间，可以认为涂层处在水的吸收阶段。在吸收阶段，水的传输主要是通过涂层中缺陷产生的扩散通道进行。可认为在水的吸收阶段为Fick扩散阶段，应满足如下关系：

式中：M和分别为时刻和饱和时的吸水量；Q和分别为时刻和饱和时涂层的吸水率；为涂层厚度，取0.4 mm；为扩散系数；为浸泡时间。

根据式（13）对深海压力–流速耦合环境下涂层相对应的数据进行线性拟合，拟合结果如图7所示。根据图7可知，斜率为0.112 77，代入式（13）算得压力–流速耦合环境下涂层的扩散系数为1.60× 10–5cm2/s。

图7 深海压力–流速耦合环境下涂层吸水动力学曲线拟合结果（0～24 h）

根据高浩东等[17]和van der Wel等[30]的研究结果表明，在深海压力–流速耦合环境条件下，水在涂层中的传输属于2阶段的Ⅱ类扩散，并非理想的Fick扩散。涂层的吸水率是由浸泡初期的Fick扩散部分Q(t)和涂层聚合物结构松弛引起的非Fick扩散部分Q(t)共同决定的。此时的吸水动力学方程应为：

式中：为常数。在前面的试验结果中，仅在0～24 h这段时间内，水在涂层中的扩散可以认为是Fick扩散。但利用式（14）计算后发现，在0～24 h这段时间内，涂层吸水率结果的相对误差较大，说明深海压力–流速耦合环境下涂层的水传输行为在浸泡初期也偏离了Fick扩散，逐渐偏向了非Fick扩散部分Q(t)，计算结果见表2。因此，进一步对式（14）进行修正，此时的吸水动力学方程为：

表2 2种扩散方程拟合结果的相对误差分析

Tab.2 Relative error analysis of fitting results of two diffusion equations

基于式（15）的拟合结果如图8所示，可以看出，模型值和实测值符合得较好。说明此时的吸水动力学方程能够正确地反映深海压力–流速耦合环境下涂层吸水率随浸泡时间的变化规律。

图8 基于Qt=QR(t)扩散方程的深海压力–流速耦合环境下涂层吸水率曲线的拟合结果

2.3 基于灰色关联理论的涂层寿命模型搭建

通过前面的分析，得出了涂层湿态附着力和吸水率随浸泡时间变化的涂层失效模型。由式（10）和式（15）分别可以搭建出由湿态附着力主导的涂层寿命模型，以及由涂层吸水率主导的涂层寿命模型，分别见式（16）和式（17）。

式中：W为涂层在时刻所测得的附着力。通过以上分析，笔者认为，在深海压力–流速耦合环境下，涂层湿态附着力的丧失和涂层的水传输过程均可以导致涂层的失效破坏。因此，通过添加权重因子来建立预测涂层寿命的总模型：

式中：1+2=1。

式（18）即为有机涂层寿命预测的数学模型。为了得到1和2在涂层总使用寿命中所占的权重，进一步利用灰色关联方法分析了湿态附着力和水传输与涂层失效的关联性，计算出了各自的关联度，并得到了1和2的权重因子。

2.4 预测及验证

灰色关联分析方法是灰色系统理论的一个分支，该方法是从不完全的信息中，对所研究的各因素通过一定的数据处理，在随机的因素序列中找出它们的相关性，得到主要影响因素。然后根据因素之间发展趋势的相似性或相异程度，来衡量因素间的接近程度。其具体分析过程如下：

首先确定反映系统行为特征的参考数列和影响系统行为的比较数列。反映系统行为特征的数据序列，称为参考数列，即母序列；影响系统行为的因素组成的数据序列，称为比较数列，即子序列。本试验中，选取各时间点下涂层电化学EIS测试所得的总阻抗值|Z|为母序列，将各时间点下涂层的湿态附着力和涂层的吸水率定义为子序列。子序列数据和母序列数据见表3。

表3 涂层相应的子序列和母序列数据

Tab.3 Corresponding subsequence and parent sequence data of coating

电化学EIS测试所用到的等效电路模型如图9所示，浸泡前涂层EIS测试过程中所用的等效电路模型为Model A，在耦合环境中服役后涂层测试所用的等效电路模型为Model B。总阻抗值|Z|在经等效电路模型拟合后，由ZSimpWin软件计算得到。等效电路模型中，s为溶液电阻，c为涂层电阻，t为电荷转移电阻。考虑到由于涂层表面的不均匀性所引起的“离散效应”，在等效电路模型中常利用常相位角元件（）代表涂层电容，其中c为涂层电容，dl为双电层电容。

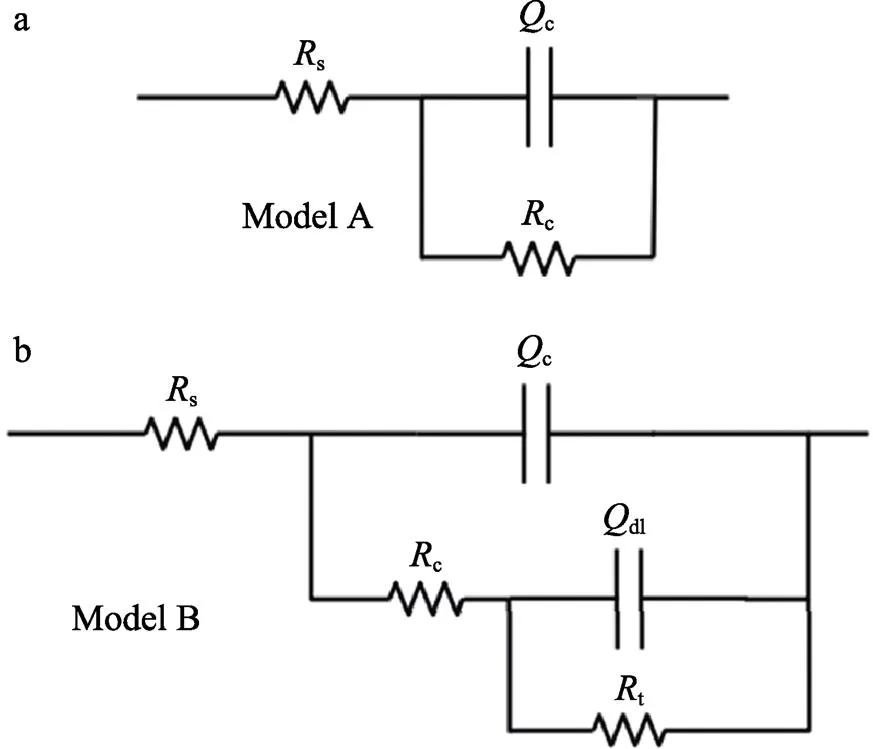
图9 涂层EIS测试所用的等效电路模型

进一步对试验原始数据进行均值化处理，而后计算各序列的关联系数，计算公式为：

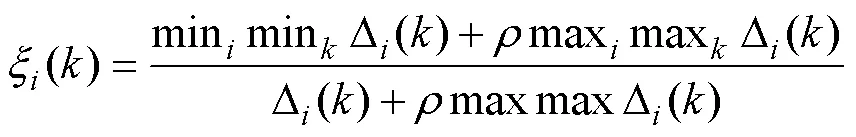
式中：为分辨系数，Î(0,∞)。一般的取值区间为(0,1)，具体取值可视情况而定。当≤0.546 3时，分辨力最好，通常取=0.5。

由于关联系数是子序列与母序列在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，因而信息过于分散，不便于进行整体性比较。因此，有必要将各个时刻（曲线中的各点）的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示。关联度w的计算公式为：

根据式（21）可以得到权重因子r为：

式（22）即为利用灰色关联度法所计算的权重因子，其结果见表4。将模型预测值和实测值进行对比，结果见表5。可以看出，通过该模型计算出来的涂层寿命预测值，与试验所得的试验值吻合较好，平均相对误差为7.56%。其中，96、120 h作为预测组，其平均预测误差为3.76%，说明该模型的精度较好。

表4 涂层湿态附着力和吸水率的关联度和权重因子

Tab.4 Correlation degree and weight factor of wet adhesion and water absorption of coatings

表5 基于灰色关联理论所得模型的预测值与实际值分析

Tab.5 Analysis of predicted and actual values of models based on grey relational theory

3 结论

1）基于深海压力–流速耦合环境下环氧–云母涂层的湿态附着力结果，构建了湿态附着力的GM(1,1)模型。该模型平均相对误差为6.65%，平均预测误差为8.05%，能正确地反映压力–流速耦合环境下涂层湿态附着力随浸泡时间的变化规律，具有良好的可靠性。

2）基于深海压力–流速耦合环境下环氧–云母涂层的吸水率试验结果推导出来的吸水动力学模型的模型值和实测值符合得较好，能够正确地反映压力–流速耦合环境下涂层吸水率随浸泡时间的变化规律。

3）进一步利用灰色关联法计算了在深海压力–流速耦合环境条件下涂层的湿态附着力和吸水率这2种影响因素在涂层失效过程中的占比，全面建立了寿命预测模型。其平均相对误差为7.56%，平均预测误差为3.76%，说明该模型精度良好，可靠性高，能准确预测涂层在深海压力–流速耦合环境下的使用寿命。

[1] NIKRAVESH B, RAMEZANZADEH B, SARABI A A, et al. Evaluation of the Corrosion Resistance of an Epoxy-Polyamide Coating Containing Different Ratios of Micaceous Iron Oxide/Al Pigments[J]. Corrosion Science, 2011, 53(4): 1592-1603.

[2] GANJAEE SARI M, SHAMSHIRI M, RAMEZANZADEH B. Fabricating an Epoxy Composite Coating with Enhanced Corrosion Resistance through Impregnation of Functionalized Graphene Oxide-Co- Montmorillonite Nanoplatelet[J]. Corrosion Science, 2017, 129: 38-53.

[3] 栾浩, 孟凡帝, 刘莉, 等. 间苯二胺-氧化石墨烯/有机涂层的制备及防腐性能研究[J]. 中国腐蚀与防护学报, 2021, 41(2): 161-168.

LUAN Hao, MENG Fan-di, LIU Li, et al. Preparation and Anticorrosion Performance of M-Phenylenediamine- Graphene Oxide/Organic Coating[J]. Journal of Chinese Society for Corrosion and Protection, 2021, 41(2): 161-168.

[4] DOBKOWSKI Z, RUDNIK E. Lifetime Prediction for Polymers via the Temperature of Initial Decomposition[J]. Journal of Thermal Analysis, 1997, 48(6): 1393-1400.

[5] DOBKOWSKI Z, RUDNIK E. Lifetime Prediction for Polymers via the Temperature of Initial Decomposition—Part 2[J]. Journal of Thermal Analysis and Calorimetry, 2002, 69(2): 693-697.

[6] DOHERTY M, SYKES J M. A Quantitative Study of Blister Growth on Lacquered Food Cans by Scanning Acoustic Microscopy[J]. Corrosion Science, 2008, 50(10): 2755-2772.

[7] MAITLAND C C, MAINE J E O. Factors Affecting the Electrolytic Resistance of Polymer Films[J]. Official Digest, 1962, 34(452): 972-991.

[8] BIERWAGEN G, TALLMAN D, LI Jun-ping, et al. EIS Studies of Coated Metals in Accelerated Exposure[J]. Progress in Organic Coatings, 2003, 46(2): 149-158.

[9] NGUYEN V N, PERRIN F X, VERNET J L. Water Permeability of Organic/Inorganic Hybrid Coatings Prepared by Sol–Gel Method: A Comparison between Gravimetric and Capacitance Measurements and Evaluation of Non-Fickian Sorption Models[J]. Corrosion Science, 2005, 47(2): 397-412.

[10] SHEVCHUK P, GALAPATS B, SHEVCHUK V. Mathematical Modelling of Ageing and Lifetime Prediction of Lacquer-Paint Coatings in Sea Water[J]. International Journal of Engineering Science, 2000, 38(17): 1869-1894.

[11] LIU Ying, WANG Jiang-wei, LIU Li, et al. Study of the Failure Mechanism of an Epoxy Coating System under High Hydrostatic Pressure[J]. Corrosion Science, 2013, 74: 59-70.

[12] LIU Rui, LIU Li, MENG Fan-di, et al. Finite Element Analysis of the Water Diffusion Behaviour in Pigmented Epoxy Coatings under Alternating Hydrostatic Pressure[J]. Progress in Organic Coatings, 2018, 123: 168-175.

[13] LIU Li, CUI Yu, LI Ying, et al. Failure Behavior of Nano-SiO2Fillers Epoxy Coating under Hydrostatic Pressure[J]. Electrochimica Acta, 2012, 62: 42-50.

[14] TIAN Wen-liang, MENG Fan-di, LIU Li, et al. The Failure Behaviour of a Commercial Highly Pigmented Epoxy Coating under Marine Alternating Hydrostatic Pressure[J]. Progress in Organic Coatings, 2015, 82: 101-112.

[15] LIU Rui, LIU Li, TIAN Wen-liang, et al. Finite Element Analysis of Effect of Interfacial Bubbles on Performance of Epoxy Coatings under Alternating Hydrostatic Pressure[J]. Journal of Materials Science & Technology, 2021, 64: 233-240.

[16] 曹京宜, 王智峤, 李亮, 等. 深海压力交变加速条件下改性石墨烯有机涂层的失效机制[J]. 中国腐蚀与防护学报, 2020, 40(2): 139-145.

CAO Jing-yi, WANG Zhi-qiao, LI Liang, et al. Failure Mechanism of Organic Coating with Modified Graphene under Simulated Deep-Sea Alternating Hydrostatic Pressure[J]. Journal of Chinese Society for Corrosion and Protection, 2020, 40(2): 139-145.

[17] 高浩东, 崔宇, 刘莉, 等. 深海压力-流速耦合环境对环氧玻璃鳞片涂层失效行为的影响[J]. 中国腐蚀与防护学报, 2022, 42(1): 39-50.

GAO Hao-dong, CUI Yu, LIU Li, et al. Influence of Simulated Deep Sea Pressured-Flowing Seawater on Failure Behavior of Epoxy Glass Flake Coating[J]. Journal of Chinese Society for Corrosion and Protection, 2022, 42(1): 39-50.

[18] MENG Fan-di, LIU Li, LIU Er-hai, et al. Synergistic Effects of Fluid Flow and Hydrostatic Pressure on the Degradation of Epoxy Coating in the Simulated Deep-Sea Environment[J]. Progress in Organic Coatings, 2021, 159: 106449.

[19] DENG Ju-long. Control Problems of Grey Systems[J]. Systems & Control Letters, 1982, 1(5): 288-294.

[20] QIAN Wu-yong, WANG Jue. An Improved Seasonal GM(1, 1) Model Based on the HP Filter for Forecasting Wind Power Generation in China[J]. Energy, 2020, 209: 118499.

[21] ZHANG Lin, WEI Xiao-hui. Prediction of Variable Amplitude Fatigue Crack Growth Life Based on Modified Grey Model[J]. Engineering Failure Analysis, 2022, 133: 105939.

[22] WANG Zheng-xin, LI Qin, PEI Ling-ling. A Seasonal GM(1, 1) Model for Forecasting the Electricity Consumption of the Primary Economic Sectors[J]. Energy, 2018, 154: 522-534.

[23] NKUBA C K, KIM S, DIETRICH S, et al. Riding the IoT Wave with VFuzz: Discovering Security Flaws in Smart Homes[J]. IEEE Access, 2021, 10: 1775-1789.

[24] XIE Wen-bo, ZHENG Hua, LI Ming-yang, et al. Membership Function-Dependent Local Controller Design for T-S Fuzzy Systems[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(2): 814-821.

[25] DU Jia-wei, WU Fang, YIN Ji-chong, et al. Polyline Simplification Based on the Artificial Neural Network with Constraints of Generalization Knowledge[J]. Cartography and Geographic Information Science, 2022, 49(4): 313-337.

[26] 耿刚强, 林杰, 刘来君, 等. 钢桥防腐蚀涂层寿命的预测方法[J]. 长安大学学报(自然科学版), 2006, 26(5): 43-47.

GENG Gang-qiang, LIN Jie, LIU Lai-jun, et al. Life Prediction System for Protective Coating of Steel Bridge[J]. Journal of Chang’an University (Natural Science Edition), 2006, 26(5): 43-47.

[27] 李瑞超. 海水中不同组分环氧涂料阴极剥离性能研究[D]. 大连: 大连海事大学, 2017.

LI Rui-chao. The Study on Cathodic Performance of Epoxy Coatings with Different Components in Seawater[D]. Dalian: Dalian Maritime University, 2017.

[28] 周立建, 穆志韬, 邢玮, 等. 基于灰色神经网络的有机涂层寿命预测研究[J]. 装备环境工程, 2011, 8(5): 62-65.

ZHOU Li-jian, MU Zhi-tao, XING Wei, et al. Study of Service Life Prediction of Organic Coatings Based on Grey Neural Network[J]. Equipment Environmental Engineering, 2011, 8(5): 62-65.

[29] MENG Fan-di, LIU Ying, LIU Li, et al. Studies on Mathematical Models of Wet Adhesion and Lifetime Prediction of Organic Coating/Steel by Grey System Theory[J]. Materials (Basel, Switzerland), 2017, 10(7): 715.

[30] VAN DER WEL G K, ADAN O C G. Moisture in Organic Coatings—A Review[J]. Progress in Organic Coatings, 1999, 37(1/2): 1-14.

Life Prediction of Organic Coatings Based on Grey System Theory in Deep-sea Pressure-Velocity Coupling Environment

CHEN Yu-fan1, MENG Fan-di1, LIU Li1, CUI Yu2, LIU Rui1, WANG Fu-hui1

(1. Joint Research Division of Northeastern University, Shenyang National Laboratory for Materials Science, Shenyang 110819, China; 2. Shi-changxu Innovation Center for Advanced Materials, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China)

The work aims to establish a life prediction model of organic coatings in the deep-sea pressure-velocity coupling environment, and predict the lifetime of organic coating in this environment. First, a wet adhesion GM (1,1) model was established according to the grey system theory and the results of wet adhesion change of the coating. Then based on the experimental results in this environment, the diffusion model of the coating water transport was established. Finally, the grey relational analysis method was used to calculate the weight factors of the two failure influencing aspects in the coating failure process and establish the mathematical model of coating failure based on these two influencing aspects. After mathematical statistics verification and experimental results comparison verification, the model had good accuracy and high reliability. The model can accurately predict the lifetime of organic coatings in the deep-sea pressure-velocity coupling environment.

deep-sea pressure-velocity coupling environment; organic coating; grey system theory; wet adhesion; water transport; lifetime prediction

2022-03-24；

2022-04-15

CHEN Yu-fan (1996-), Male, Postgraduate, Research focus: failure behavior and protection of organic coatings in deep-sea extreme environment.

孟凡帝（1988—），男，博士，副教授，主要研究方向为海洋环境有机涂层研究、深海环境金属腐蚀与防护。

Corresponding author：MENG Fan-di (1988-), Male, Doctor, Associate professor, Research focus: organic coatings in marine environment and metal corrosion and protection in deep sea environment.

陈宇凡,孟凡帝,刘莉,等. 深海压力–流速耦合环境下基于灰色系统理论的有机涂层寿命预测研究[J]. 装备环境工程, 2023, 20(2): 064-072.

TG174.4

A

1672-9242(2023)02-0064-09

10.7643/ issn.1672-9242.2023.02.009

2022–03–24；

2022–04–15

国家自然科学基金（51901040）

Fund：The National Natural Science Foundation of China (51901040)

陈宇凡（1996—），男，硕士研究生，主要研究方向为深海极端环境下有机涂层的失效行为与防护。

CHEN Yu-fan, MENG Fan-di, LIU Li, et al.Life Prediction of Organic Coatings Based on Grey System Theory in Deep-sea Pressure-Velocity Coupling Environment[J]. Equipment Environmental Engineering, 2023, 20(2): 064-072.

责任编辑：刘世忠