Sm+1中超曲面的一个Moebius刚性定理*

马江涛， 管山林， 李虹

(云南师范大学 数学学院,云南 昆明 650500)

1 引言

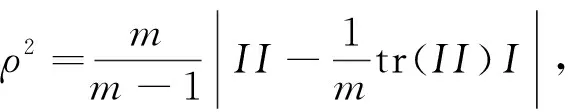
(1)

(2)

Bij=ρ-1(hij-Hδij),

(3)

其中Hessij和∇为I=dx·dx在基底ei下的Hesse矩阵和梯度算子.称B的特征值为x的Moebius主曲率.Rm+3是m+3维欧式向量空间，定义内积〈·,·〉1如下:

〈X,Y〉1=-x0y0+x1y1+x2y2+x3y3+…+xm+2ym+2,

(4)

其中

X=(x0,x1,x2,…，xm+2)，Y=(y0,y1,y2,…，ym+2)；

定义

(5)

定义

Qm+1:={[Y]∈RPm+2|〈Y,Y〉1=0}

(6)

为RPm+2的二次曲面.

本文运用Moebius几何的方法，得到如下定理.

定理1设x:Mm→Sm+1(m>3)是无脐浸入超曲面，B为Moebius第二基本形式，则有不等式

等号成立当且仅当Mm是单参数球族的包络.

2 Sm+1中超曲面的Moebius不变量

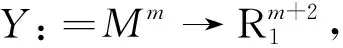
(7)

设Δ为(M,g)的Laplace算子，则

〈ΔY,ΔY〉=1+m2κ；

(8)

设{E1,E2,…，Em}是(M,g)的一个局部标准正交基，{ω1，ω2，…，ωm}为其对偶基.由Ei(Y)=Yi,得

〈Yi,Yj〉=δij,1≤i,j≤m.

(9)

定义

(10)

则

〈Y,Y〉=〈N,N〉=0,〈Y,N〉=1,〈Yi,Y〉=〈Yi,N〉=0；

(11)

〈Y,dY〉=0,〈ΔY,Y〉=-m,〈ΔY,Yk〉=0,1≤k≤m.

(12)

因此

span{N,Y}⊥span{Y1,Y2,…,Ym}.

(13)

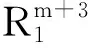
(14)

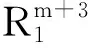
1≤i,j,k,l≤m.

其结构方程为

(15)

(16)

(17)

(18)

其中{ωij}是Moebius度量g诱导的联络形式.由(16)-(18)可知

(19)

称B为x的Moebius第二基本形式，Φ为x的Moebius形式.

定义Bij的一阶协变导数为

(20)

那么(15)-(18)蕴含可积条件为[3]

Bij,k-Bik,j=δijCk-δikCj,

(21)

Rijkl=BikBjl-BilBjk+(δikAjl+δjlAik-δilAjk-δjkAil),

(22)

(23)

其中Aij,k,Bij,k和Ci,j是A,B和Φ关于g诱导的联络的协变导数在标准基下的分量.由(21)得

(24)

由(22)式得

(25)

3 定理1的证明

证明由Weyl曲率张量的定义

(26)

可得

(27)

因为W为无迹张量，因此

(28)

(29)

由(22)、(23)、(25)和(29)可以得到

(30)

由(22)、(26)和(30)可得

(31)

由(28)和(31)式可得

(32)

将(31)式代入(32)可得

(33)

最终得到

(34)

由(34)得

(35)

所以

(36)

等号成立当且仅当Mm是共形平坦的,再根据E. Cartan定理[4]知Mm是单参数球族的包络.定理得证.