实际电极系系数的有限元模拟研究

2023-03-08刘子强齐兴华王有龙

甘肃科技 2023年1期

刘子强，齐兴华，王有龙

（1.新疆煤田地质局一五六勘探队新疆乌鲁木齐 830023；2.新疆工程学院新疆乌鲁木齐 830022）

高密度电阻率法（HDR）是一种网络勘探方法。根据岩石和土壤导电性的差异，研究了人工稳定电流场作用下土壤中导电电流的分布。现场测量时，所有电极（几十到几百个）都可以放置在观测段的测量点上。然后利用程控电极转换装置和微机工程机电测量仪实现数据的快速自动采集。将测量结果发送到微机后，还可以对数据进行处理，并给出地电剖面分布的图形结果[1-2]。

电阻率采集过程中，电极系系数是将测得的电阻值转换为电阻率值的关键系数。一般认为，该系数主要由电极间的相互位置决定，其中α排列的电极系系数理论计算公式如下：

式中：K为电极系系数，单位为m；AM、AN、BM、BN为电极间距，单位为m。

如公式（1）所示，电极系系数K是一个仅仅与各电极之间的距离相关的数值，但当电阻率测量装置形式和极距确定，K值便可以通过公式进行计算[3-4]。但是在实际使用过程中，所使用的电极材料和大小不同的电阻率剖面仪制造商不同和地层的深度是不同的，由于人为因素和环境因素，有时可能使用不同的供电方法或电极并非完全插入到地层[5]。这些都可能导致实际电极系系数与理论电极系系数之间存在差异，导致所计算出的视电阻率与真电阻率之间的误差较大。

为了使计算得出的视电阻率与真电阻率之间的误差变小，有必要对各种因素对实际电极系系数的影响开展研究，为校正影响奠定基础。因此，提出了一种基于COMSOL的模拟计算方法[6-8]，利用有限元法建立一种电阻率法的三维正演模型对实际电极系系数进行模拟计算，重点分析了不同电极半径、电极插入地层深度和不同电极间距的条件下对实际电极系系数的影响，从而加深从业者对电极系系数的理解，对在生产用采用高密度电法及与之类似的其他电阻率测量方法时能够提高探测精度，有较好的参考价值。

1 模型建立

文章从3个方面进行了论述。第一，在保持电极材料、电极间距、电极埋入地层深度等因素不变的情况下，通过改变电极半径来探讨电极半径对实际电极系系数的影响。第二，在保持电极材料、电极间距、电极半径等各因素不变的情况下，只改变电极插入地层的深度，以探讨电极插入地层深度对实际电极系系数的影响。第三，在保持电极材料、电极插入地层深度、电极半径等各因素不变的情况下，通过调整电极间距来探讨电极间距对实际电极系系数的影响。

在解决简单模型的模拟问题时，使用偏微分方程即可满足需求，但是当几何结构或者物理场复杂时，偏微分方程便无法取得解析解。将复杂模型进行离散化从而构建近似方程并获取近似解以达到对复杂模型模拟的目的即是有限元法的本质。COMSOL Multiphysics是一款基于有限元法的模拟软件，近年来被各领域学者广泛使用，取得了良好的效果，本文即采用该软件开展上述研究。

1.1 理论基础

在地球物理勘探中，经常通过对目标地质体电阻率的测量来完成对其大小、形状、矿物种类、含量等多方面性质的判断。其中，经常用到的一种方法就是电阻率剖面法。电阻率剖面法是指A、M、N、B电极距保持不变，同时沿—定剖面方向逐点观测视电阻率（ρs），研究剖面方向地下一定深度的岩、矿石电阻率变化的一组方法。

在地下介质均匀各向同性的条件下，电阻率计算式：

式中：R为电阻率，单位为Ω·m；

U为电压值，单位为V；

I为电流值，单位为A。

由公式（2）可知在模型中只要能够获取到除K以外的物理量则可求出实际的K值。

对于时变电场和电流，在磁效应可以忽略不计的情况下，物理场应遵循电流守恒方程：

式中：J为电流密度，单位A/m2；

ρ为电荷密度，单位C/m3；

t为时间，单位为s。

其中

式中：σ为电导率，单位为S/m；

V为电压，单位为V（伏特）；

E为电场强度，单位为V/m。

1.2 模型参数

模型由地层和电极棒组成，如下图1所示，其中正方体为地层，其长宽高均为100 m，其电导率设定为1 S/m，即电阻率为1 Ω·m。其上4个小圆柱为铜电极，电极直径初始0.004 m，电极初始间距2 m，自左起依次为A、M、N、B电极，其中A电极和B电极分别为正负供电电极，向地层中供直流电流，M电极和N电极为测量电极，测量所处位置的电压。模型中设定A电极与B电极之间的电流恒定为1A，并通过探针的形式测量M点电压及N点电压。

图1 模型示意图

为满足使用有限元法进行模拟的精确度，在地层中所使用的网格最大为1 m，在电极上采用的网格最大为0.001 m，网格剖分后的结果如图2所示。为保证模型计算精度的可靠，特采用了100 m尺寸的地层模型，保证地层的尺寸在研究范围内足够大以减小电场边界效应对模拟结果的影响，因此，对模型的边界未进行虚拟域或其他边界设置。

图2 网格剖分结果

2 模拟结果及分析

初始状态下的电场分布情况如图3所示。由图3可以看出，A电极电势最大，B电极电势最小，M电极和N电极电势差别难以用肉眼观察但软件可通过探针进行准确探测。

图3 电场分布图

在此情况下理论电极系系数计算过程如下：

AM=2 m，AN=2 m，BM=2 m，BN=2 m代入公式（1）中，得出理论电极系系数K=12.56，单位为m。

实际电极系系数计算过程如下：

地层电阻率R为1 Ω·m，A电极与B电极之间的电流I为1 A，模拟结果显示M电的电压为1.8313 V，N点的电压为1.754 7 V，因此M、N电极的电压差U为0.076 6 V。将上述物理量带入公式（2），可知此时的电极系系数为：

由上述计算过程可以看出，在初始情况下，实际电极系系数与理论电极系系数并不完全一致，存在由各种因素导致电极系系数有较大变化从而影响电阻率计算精度降低的可能性。

2.1 当电极半径改变时的模拟结果

在其他条件均不改变时，电极半径从0.002 m逐步增加到0.007 m时，通过仿真计算得到的实际电极系系数的变化，并与由（1）式得到的理论电极系系数进行比较，其结果见图4。

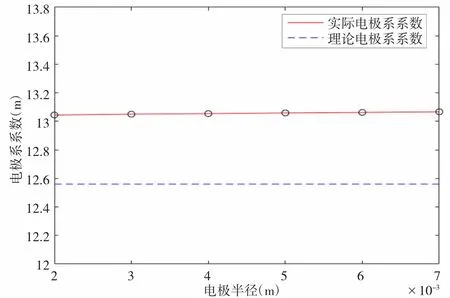
图4 电极半径对电极系系数的影响变化模拟结果

从图4中可以看出，实际电极系系数与理论电极系系数的差值随着电极半径的增大而增大。但是从变化的程度可以看出，电极的半径变化对电极系系数的影响非常有限，因此在实际使用过程中，采用常用的电极基本不需要对电极系系数进行半径方面的校正。

2.2 当电极插入地层深度改变时的模拟结果

当电极插入地层深度逐渐由0.1 m逐渐变为0.5 m且其他条件均不改变时，得出的实际电极系系数的变化并与由公式（1）得出的理论电极系系数作对比如图5所示。

图5 电极插入地层深度对电极系系数的影响变化模拟结果

从图5中可以看出，实际电极系系数随着电极插入地层深度的增大而增大，且与理论电极系系数的差值越来越大，因此，对电极插入地层深度为0.45 m时的电场分布情况（如图6所示）开展了相关研究。

图6 插入深度为0.45 m时的电场分布图

通过图6可看出，A电极供电是电势最大，B电极电势最小，M电极和N电极电势近乎相等，但与图3未改变地层深度时的电场分布情况相比，电极附近的电场分布情况发生了明显的改变，电场强度最高的地方与电极的深入程度直接相关，因此，随着电极插入程度的加深，电场的整体分布发生了与理想电极系情况下的点电极电场分布有了很明显的区别，这种电场分布的变化最终导致了实际电极系系数与理论电极系系数之间的差别随着插入深度的变化而发生明显变化。

2.3 当电极间距改变时的模拟结果

在其他条件不变的情况下，在电极间距从2 m逐步增加到6 m时，得到了实际的电极系系数的变化，并将其与公式（1）中的理论电极系系数进行比较如图7所示。

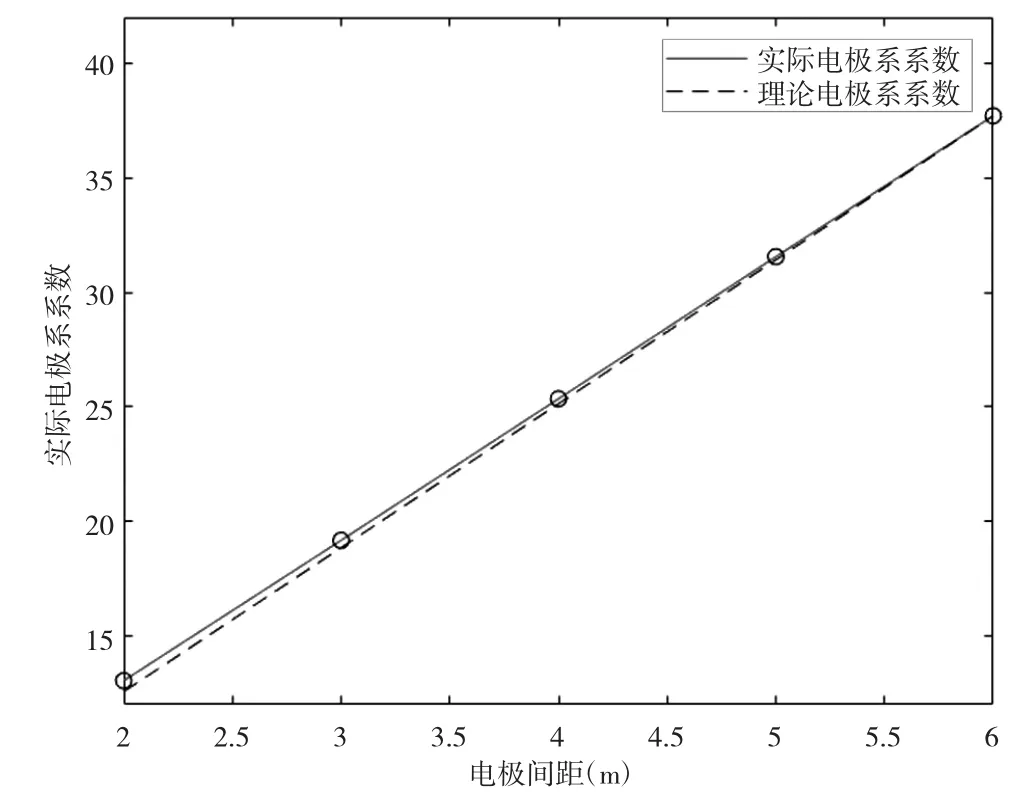
图7 电极间距对电极系系数的影响变化模拟结果

从图7中可以看出，当电极距增大时，实际电极系系数与理论电极系系数之间的差值逐渐减小，在达到一定的电极距之后二者基本趋于相同。这是由于在电极尺寸和插入地层深度不变的情况下，随着电极距的增大，整个电极系的尺寸在不断的增大，因此，电极的相对尺寸越来越小，即电极系的工作状态越来越趋近于点电极时的工作状态，从而导致实际电极系系数与理论电极系系数越来越接近。这也说明，在使用较大电极距时，电极系系数可以近似采用理论电极系系数，而在电极距较小时，则应对电极系系数进行相应的校正以降低视电阻率的计算误差。