基于深度学习的飞行器故障情况下可配平能力快速预示方法

武天才，王宏伦，刘一恒，杨志远，余跃

1.北京航空航天大学，北京 100191

2.北京航天自动控制研究所，北京 100854

飞行器在复杂的大气环境中长期飞行时，由于部件老化和烧蚀，极有可能引发执行机构故障，从而导致飞行性能下降甚至任务失败[1-3]。因此，当执行机构出现故障时，快速准确地判断飞行器故障情况下的可配平能力对飞行安全至关重要[4]。针对可重复使用运载器X-33 在进场着陆段的可配平能力问题，国外学者Shaffer和Fahroo等[5-6]对气动舵故障下的容错最优轨迹进行了研究，并将故障对配平能力的影响引入三自由度模型中，提升了飞行器的容错能力。中北大学王文虎等[4]针对亚轨道飞行器在上升段摆动发动机故障下的配平能力问题，采用相容性判定方法进行了分析，并给出配平能力不足时的应急策略。西北工业大学解永锋等[7]采用非线性控制分配算法进行了亚轨道飞行器返回段气动舵面故障下的配平能力分析。这类方法本质上属于数值优化算法，在进行配平能力分析时，具有求解时间较长的缺点。对具有较快飞行速度的飞行器而言，如果无法及时分析故障带来的影响，极有可能导致事故发生。

近年来，人工智能技术的快速发展为飞行器技术的研究提供了新的技术途径[8-10]。余跃和章吉力等[11-13]利用深度学习方法进行飞行器落点的映射，大大提升了预测校正算法的实时性。吴健发和王延祥等[14-15]利用深度学习方法在线优化算法参数，有效地提升了飞行器路径规划的自适应能力和快速性。

基于上述分析，针对飞行器故障情况下的配平能力分析问题，本文首先将飞行器旋转配平条件转化为优化问题，利用二次规划方法进行求解。然后，为进一步提升可配平能力剖面求取的快速性，借助深度学习的强非线性拟合能力，提出一种基于深度学习快速预示方法。

1 飞行器旋转配平问题描述

1.1 作用在飞行器上的气动力矩

在机体坐标系下，作用于飞行器的气动力矩可分解为滚转力矩Mx、偏航力矩My和俯仰力矩Mz

1.2 执行机构布局

本文研究的轴对称飞行器的执行机构为气动舵，采用X 字形布局，双向偏转，执行机构布局示意图如图1 所示。等效舵偏δx,δy,δz与实际执行机构舵偏δ1,δ2,δ3,δ4的关系为

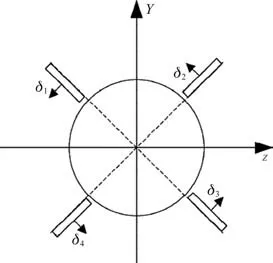
图1 飞行器执行机构布局示意图[1]Fig.1 Schematic diagram of vehicle actuator[1]

式中，B为控制分配矩阵。

1.3 执行机构故障模型

飞行器执行机构最常见的故障是增益故障和偏置故障，可用公式表示为

式中，δc=[δ1c,δ2c,δ3c,δ4c]T，表示期望的执行机构舵偏角；δ=[δ1,δ2,δ3,δ4]T，表 示 实 际 的 执 行 机 构 舵 偏 角；Λ=diag{λ1,λ2,λ3,λ4}，表示增益故障，增益故障取值范围为0 ≤λi(i= 1,2,3,4) ≤1；ρ=[ρ1,ρ2,ρ3,ρ4]T，为偏置故障。

当λi和ρi取不同值时，可以代表不同的故障类型。例如，λi= 0,ρi=ρˉi表示飞行器出现卡死故障；0 ≤λi≤1,ρi=0表示飞行器出现有效性损失故障。

1.4 飞行器旋转配平条件

能旋转配平飞行器的必要条件是：所有执行机构作动产生的力矩与机体产生的力矩大小相等，方向相反，可表示为

飞行器旋转配平条件可描述为如下的控制分配问题，该控制分配的首要任务是确定最优舵偏角使控制不足区域最小，即式（4）两端的差最小，用公式表示为

如果式（5）的值为零，则表明飞行器可旋转配平，处于可控状态；如果式（5）的值非零，则表明飞行器不可旋转配平（配平不足），处于失控状态。此时，迎角、侧滑角的配平不足区域可以绘成一张图，作为限制轨迹的飞行包线界，在设计迎角、侧滑角剖面时应避免配平不足区域。

2 基于二次规划的可配平能力求解方法

为方便求解飞行器可旋转配平区域，可将式（5）的优化问题进一步改写为如下的二次规划问题

当执行机构存在故障时，式（6）可进一步修正为

式中，δ=Λδc+ρ，fuBδ表示执行机构存在故障时的由执行机构作用引起的力矩系数项。

在气动系数给出的迎角和侧滑角范围内，进行遍历计算式（7）的值，则可以得到当前执行机构故障情况下可配平和无法配平的迎角—侧滑角二维区域。图2给出了执行机构δ2卡死在-6°时的配平能力示意图，其中，红色区域表示无法配平区域，蓝色区域表示可配平区域。

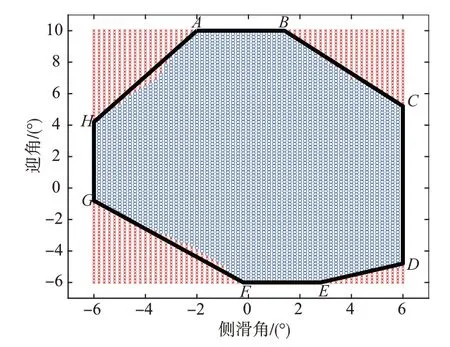
图2 执行机构δ2卡死在-6°时的配平能力示意图Fig.2 Schematic diagram of trim capability when δ2 is stuck at -6°

在进行飞行器可配平能力求解时，需要对迎角和侧滑角二维平面进行遍历求解，即每次均需进行对式（7）的优化求解，该过程是一个极其耗费时间的过程，难以在线应用。

通过对不同执行机构故障情况下配平能力示意图进行分析，可以发现可配平的区域可以通过8 个点进行包络表示，分别是：A(αA,βA)点：迎角取最大值时，侧滑角可取的最小值；B(αB,βB)点：迎角取最大值时，侧滑角可取的最大值；C(αC,βC)点：侧滑角取最大值时，迎角可取的最大值；D(αD,βD)点：侧滑角取最大值时，迎角可取的最小值；E(αE,βE)点：迎角取最小值时，侧滑角可取的最大值；F(αF,βF)点：迎角取最小值时，侧滑角可取的最小值；G(αG,βG)点：侧滑角取最小值时，迎角可取的最小值；H(αH,βH)点：侧滑角取最小值时，迎角可取的最大值。

按顺序依次连接A、B、C、D、E、F、G、H、A，则可以得到一个用于包络可配平区域的多边形，如图2中黑色实线所示。

为进一步提高飞行器可配平能力剖面求解的效率，本文在基于二次规划的可配平能力求解方法的基础上，进一步结合深度学习的强大拟合能力，利用深度神经网络进行迎角和侧滑角二维平面遍历优化过程的拟合，这样可大大提升计算实时性。

3 基于深度学习的飞行器故障情况下可配平能力快速预示方法

3.1 可配平能力预示网络结构

利用深度全连接神经网络的非线性拟合能力来预示可配平能力比较合适[11]，网络结构如图3所示。

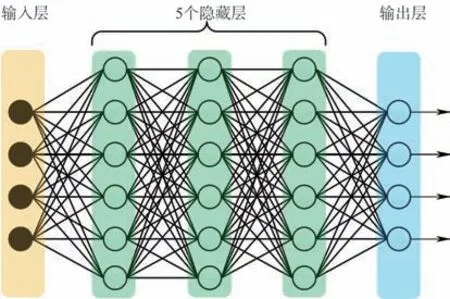
图3 可配平能力预示网络结构图Fig.3 Schematic diagram of network structure for trim capability prediction

对于隐含层层数和节点数的选取目前尚没有相关理论支撑，拟合精度会随着隐含层层数和节点数的增加而提高。但是，随着隐含层层数和节点数的增加，计算量也会同时增加。因此，在选择层数和节点数时需要综合考虑。本文将隐含层设置为5层，每个隐含层节点设置为20个。

可配平能力预示网络的输入设置为：执行机构故障Λ,ρ和由迎角和侧滑角引起的力矩系数项。可配平能力预示网络的输出设置为：用于包络可配平区域的多边形的8个顶点的迎角和侧滑角的值。

执行机构故障参数Λ^ ,ρ^ 可采用参考文献[2]中给出的基于深度学习的故障诊断方法获得；当存在气动参数不确定性时，由迎角和侧滑角引起的力矩系数项的估计值可采用参考文献[11]给出的估计方法计算获得。

3.2 可配平能力预示网络样本生成方法

有效的训练样本是检验可配平能力预示网络有效性的前提，本文在不同的执行机构故障情况下，采用第2节所述的基于二次规划的可配平能力求解方法进行离线计算，可以得到在不同气动参数摄动和执行机构故障情况下用于表征可配平区域多边形的8个顶点的迎角和侧滑角的值。

在样本生成中，执行机构故障设置为：执行机构δi(i=1,2,3,4)存在有效性损失与卡死故障，其中，有效性损失范围为：0～100%，卡死故障范围为-15°～15°。气动参数摄动也在(- 30%, 30%)的范围内随机取值。在上述条件下进行大量的数值仿真，并采集仿真过程中由迎角和侧滑角引起的飞行器机体力矩系数估计项；飞行器执行机构故障值Λ^ ,ρ^ 和多边形顶点A、B、C、D、E、F、G、H的迎角和侧滑角数据作为训练样本。在进行遍历求解时，有效性损失的间隔为1%，卡死故障的间隔为0.5°，气动参数摄动的间隔为5%，共生成19542692组数据。

3.3 可配平能力预示网络训练方法

可配平能力预示网络使用上述方法生成的样本进行训练，可配平能力预示网络训练方法结构如图4所示。

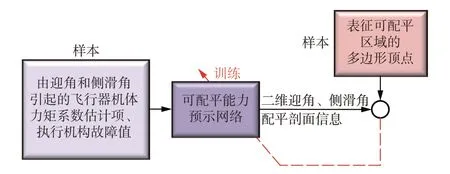
图4 可配平能力预示网络训练方法结构图Fig.4 Schematic diagram of network training method for trim capability prediction

可配平能力预示网络的损失函数设计为均方误差形式，即一个批量数据中可配平预示网络的估计值和样本真实值之差平方的平均值

式中，N表示批量数据的大小，= [αA,βA,αB,βB,αC,βC,αD,βD,αE,βE,αF,βF,αG,βG,αH,βH]T表 示 样 本 真 实 值，LNL+1=表示可配平能力预示网络输出的估计值。

采用Adam优化器根据损失值计算梯度来更新可配平能力预示网络的参数。经过充分的训练迭代，最终能够得到一个可以进行可配平区域预示的深度网络。通过使用训练好的可配平能力预示网络在未经训练的样本上进行测试，来验证可配平能力预示网络的性能。

根据3.2 节所述方法生成的样本，将80%的样本作为训练集，将20%的样本作为验证集，进行网络训练，图5给出了训练过程中训练集和验证集的损失曲线。可以发现，随着训练轮数的增加，训练集和验证集的损失曲线不断下降，最终降至0.15以下，体现出可配平能力预示网络的有效性。

图5 可配平能力预示网络训练损失曲线Fig.5 Training loss curve of network for trim capability prediction

4 仿真分析

本节通过数值仿真来验证所提可配平能力预示方法的有效性。仿真情况设置为：气动参数摄动30%，执行机构δ1出现卡死在6°的故障。飞行器的初始状态为：H=20km,V= 1275m/s，α=β=γv=0°，wmx=wmy=wmz=0 (°)/s。

仿真结果如图6所示，可以发现在气动参数存在摄动、执行机构出现卡死故障时，可配平的迎角—侧滑角剖面明显减小，图6 中黑色实线是根据实际气动参数和实际故障通过二次规划方法求得的，红色虚线是通过所提可配平能力预示方法求得的，可以发现预示的结果和真实结果差别很小。为定量说明可配平能力预示的有效性，统计了可配平能力预示方法的预示误差（见表1），可以发现，8 个顶点中迎角预示最大误差的绝对值为0.16°，侧滑角预示最大误差的绝对值为0.41°，可配平能力预示方法达到了较高的精度，验证了所提预示方法的有效性。为进一步验证所提可配平能力预示方法的有效性，在3.2节所述的执行机构故障范围和气动参数摄动范围内随机选取100 种情况，进行蒙特卡罗仿真验证。为避免重复，图7 给出蒙特卡罗仿真中对A点的迎角值的预示效果的统计图和预示误差的统计图，可以发现预示误差的绝对值保持在0.5°范围内，验证了所提预示方法的鲁棒性和有效性。图8给出蒙特卡罗仿真中预示方法与二次规划方法计算耗时的统计图，可以发现可配平能力预示方法计算耗时在0.003s 左右，远小于二次规划方法的4.5s左右，验证了所提预示方法的实时性。

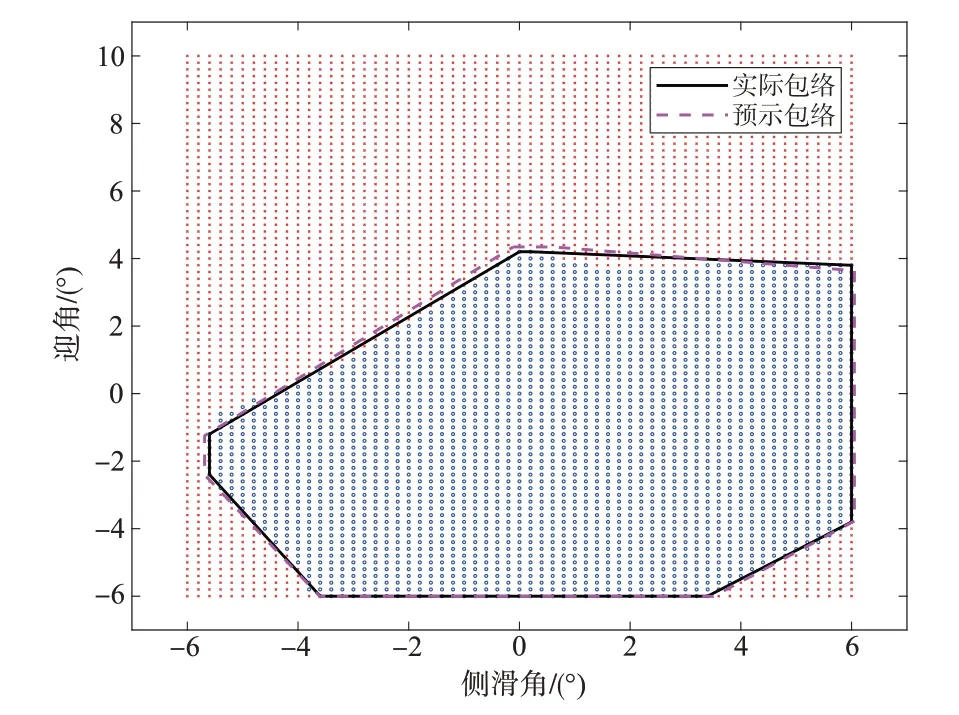
图6 可配平能力预示方法结果图Fig.6 Result curve of the trim capability prediction method

表1 可配平能力预示结果误差统计表Table 1 Result error statistics of the trim capability prediction method

图7 蒙特卡罗仿真预示结果统计图Fig.7 Statistical curve of Monte Carlo simulation results of the trim capability prediction method

图8 蒙特卡罗仿真计算耗时统计图Fig.8 Statistical curve of Monte Carlo simulation calculation time results of the trim capability prediction method

5 结论

本文针对飞行器在执行机构故障条件下配平能力受限的问题，为满足飞行器对故障情况下可配平能力剖面求取的准确性和快速性的要求，结合深度学习强大的拟合能力，提出一种基于深度学习的飞行器故障情况下可配平能力快速预示方法。从仿真结果可得所提方法的预示误差保持在0.5°量级，计算耗时保持在10-3s量级，表明该方法具有较高的鲁棒性和较强的实时性。