基于无参数高效算法的近红外光谱模型传递研究

刘翠玲 徐金阳 孙晓荣 张善哲 昝佳睿

(1.北京工商大学人工智能学院，北京 100048；2.北京工商大学食品安全大数据技术北京市重点实验室，北京 100048)

0 引言

近红外(Near infrared，NIR)[1-2]光谱技术因其快捷、无损、绿色等特点，目前已广泛应用于食品[3-5]、医药[6]和农业[7]等领域。但是，随着近红外光谱仪发展的多样性，不同光谱仪间的多元校正模型无法实现共享，重新建立校正模型需要大量的人力和财力。解决这类问题的方法称为模型传递[8](Calibration transfer)，其核心思想是消除样本在不同光谱仪器间测量信号的差异，从而实现校正模型的共享。

模型传递分为有标样传递与无标样传递[9]。近年来，国内外学者对有标样模型传递算法应用进行了研究。温晓燕等[10]利用直接标准化(Direct standardization，DS)和分段直接标准化(Piecewise direct standardization，PDS)算法对甲醇汽油进行模型传递研究；BROUCKAERT等[11]采用斜率偏差校正法(Slope/bias，S/B)对工业液体洗涤剂的成分进行模型传递研究。其次，国内外学者也对无标样模型传递算法的应用进行了研究。宋海燕等[12]将有限脉冲响应(Finite impulse response，FIR)算法应用到土壤有机质的模型传递研究；WANG等[13]将稳定竞争自适应重加权采样(Stability competitive adaptive reweighted sampling，SCARS)算法应用在树叶叶绿素浓度模型传递的研究。以上算法均实现模型传递，但方式相对单一且独立，只能选择有标样传递或无标样传递的其中一种方式实现，无法将两种方式联合应用，导致传递模型的适用范围较小。

无参数高效模型传递算法(Parameter-free and efficient calibration enhancement，PFCE)[14]根据有无标准样品分为无标样传递PFCE(Non-supervised PFCE，NS-PFCE)算法和有标样传递PFCE(Full-supervised，FS-PFCE)算法。PFCE算法将两种传递方式联合应用，具有效率高、设置简单的优点，并成功应用于药品[14]、植物叶片[15]、水果[16]模型传递的研究。

本文采用PFCE算法结合偏最小二乘回归(Partial least squares，PLS)建立传递模型，分别实现食用油酸值与过氧化值的有标样与无标样传递。并与经典的3种有标样传递算法和2种无标样传递算法进行对比，以期将模型传递更好地应用于近红外光谱检测。

1 材料与方法

1.1 实验仪器

实验在北京工商大学光谱技术与品质检测实验室完成，光谱检测仪器为Bruker公司的VERTEX-70型傅里叶红外光谱仪和MATRIX-F型傅里叶红外光谱仪。仪器参数见表1。

表1 光谱仪器和参数

主机和从机分别对同一样品进行光谱采集，采集范围为9 000～5 000 cm-1；光谱采集参数设置：样本扫描次数为32；背景扫描次数为32；光阑 6 mm；扫描频率10 kHz。

1.2 实验材料

为了构建食用油通用模型，选取北京古船食品有限公司的5种食用油样品，共计129个，其中包含19个玉米油、25个芝麻香油、56个大豆油、5个橄榄油、24个小磨香油样本。并依据文献[17-18]测定所有食用油样本酸值与过氧化值。

1.3 样品划分

在近红外光谱模型传递分析中，通常把样本划分成训练集和预测集。光谱-理化值共生距离(Sample set partitioning based on joint x-y distances，SPXY)[19]是一种有效的样品集划分方法，原理是分别采用光谱数据和样本理化值作为参数特征计算样品间距离，以保证最大程度表征样本分布，增加样本间差异性和代表性，并提高模型稳定性和准确性。

1.4 PFCE模型传递算法

根据使用场景不同，无参数高效模型传递算法(PFCE)分为NS-PFCE无标样模型传递算法和FS-PFCE有标样模型传递算法。NS-PFCE仅使用食用油样本光谱信息实现模型传递，而FS-PFCE则需要食用油样本的光谱信息与理化值信息共同作用实现模型传递。

1.4.1主机PLS多元校正模型建立

偏最小二乘回归(PLS)[20]是一种经典的统计学方法，已经成为衡量校正模型效果的最佳标准。采用PLS方法建立食用油的多元校正模型，并通过选择最佳潜在变量的数量来优化模型。

主机光谱仪采集的样品光谱数据记为Xmaster并与样本理化值y建立主机的线性回归模型，并得到预测值，即

(1)

式中b0,master——主机模型截距

bmaster——主机模型回归系数

e——和y之间的预测误差

1.4.2NS-PFCE无标样模型传递算法

从机光谱仪采集的样品光谱数据记为Xslave，将主机模型截距b0,master和回归系数bmaster代入NS-PFCE算法的成本函数，使从机模型尽可能接近主机模型，即：主机模型预测值与从机模型预测值误差最小，从而寻找最优的从机模型截距b0,slave和回归系数bslave，即

(2)

式中 corr(·)——bmaster和bslave间的相关系数运算函数

rthres——约束阈值

为了加快函数收敛速度并减少搜寻空间，在主机模型与从机模型的回归系数间施加相关系数的约束阈值rthres，且为了防止出现欠拟合与过拟合的情况，将rthres设置为0.98。

1.4.3FS-PFCE有标样模型传递算法

相比NS-PFCE无标样模型传递算法，FS-PFCE有标样模型传递算法不仅需要主机光谱数据Xmaster与从机光谱数据Xslave，还要食用油样本理化值真实值y。相似地，通过FS-PFCE算法的成本函数得到最优的从机模型的截距b0,slave和回归系数bslave，即

(3)

FS-PFCE算法的成本函数不仅计算了主机光谱与从机光谱的预测误差，还计算了真实值与从机预测值的误差。同样，防止出现欠拟合与过拟合的情况，将rthres设置为0.98。

1.5 模型传递评价指标

模型的评价指标选择决定系数(Correlation coefficient of cross-validation，R2)、训练集均方根误差(Root mean square error of calibration，RMSEC)和预测集均方根误差(Root mean square error of prediction，RMSEP)。R2越接近1且RMSEC与RMSEP越小，表明模型传递效果越好。

2 结果与分析

如图1所示，主机和从机所采集的食用油样品的平均吸光度在波段9 000～5 000 cm-1之间,共2 074个波数点。可以看出主机光谱和从机光谱存在明显的非线性差异，吸光度差值在波段 9 000～8 750 cm-1存在较大偏差。

图1 主、从机的食用油平均吸光度及光谱差值

2.1 样本划分

采用SPXY算法按照比例3∶1选取97个食用油样本作为训练集，32个样本食用油作为验证集，用于建立酸值和过氧化值定量分析模型。食用油样本酸值和过氧化值的数据集划分如表2所示，其中预测集的数值范围均在训练集之内，表明预测集可以对模型的性能进行验证。

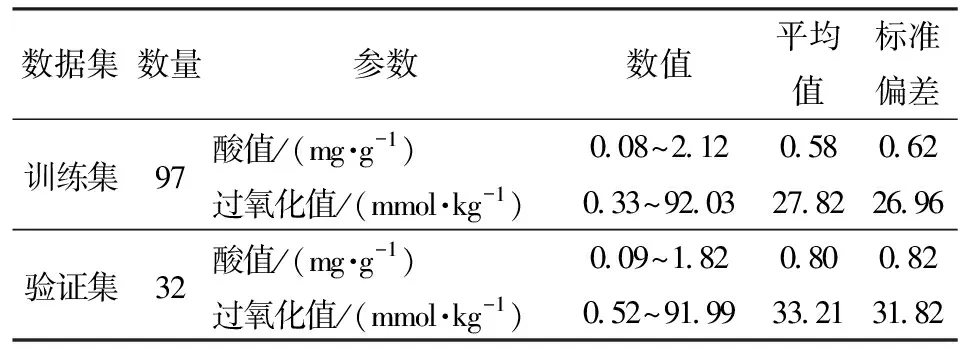
表2 食用油样品数据集划分

2.2 主机模型预测结果

为了消除噪声干扰等因素对建模效果的影响，分别采用Savitzky-Golay(S-G)平滑卷积[21]、多元散射校正(Multiplicative scatter correction，MSC)[22]、标准正态变量变换(Standard normalized variate，SNV)[23]、一阶导数和二阶导数[24]共5种预处理算法处理光谱数据。选择最优预处理算法后建立主机酸值与过氧化值偏最小二乘校正模型，不同预处理条件下主机PLS校正模型预测结果如表3、4所示。

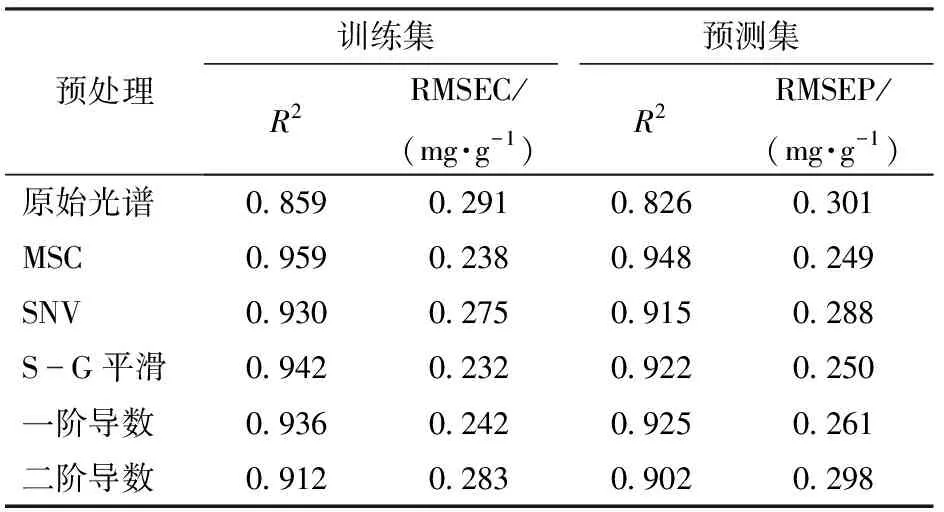
表3 不同预处理条件下主机PLS校正模型酸值预测结果

表4 不同预处理条件下主机PLS校正模型过氧化值预测结果

从表3、4可看出，采用5种不同预处理算法处理食用油光谱的建模效果比直接使用原始光谱的建模效果均有提升。其中，主机酸值模型MSC算法预处理效果最优，预测集决定系数R2达0.948，预测值均方根误差RMSEP为0.249 mg/g。主机过氧化值模型SNV算法预处理效果最优，预测集决定系数R2达0.954，预测值均方根误差RMSEP为7.749 mmol/kg。

MSC和SNV算法的本质是消除样品表面散射和光程变化等因素对光谱产生的影响，故二者算法不同程度地消除了食用油因液体表面张力引起的散射，所以预测效果优于其他算法，也有效提高了模型预测精度。

2.3 PFCE算法模型传递及预测结果

按照PFCE算法分类进行NS-PFCE无标样模型传递算法与FS-PFCE有标样模型传递算法。利用NS-PFCE与FS-PFCE算法得到的最优截距和回归系数分别构建从机预测模型，并将从机的32个食用油样本分别代入以上两种模型进行预测，预测的食用油酸值散点图如图2、3所示，预测的食用油过氧化值散点图如图4、5所示。

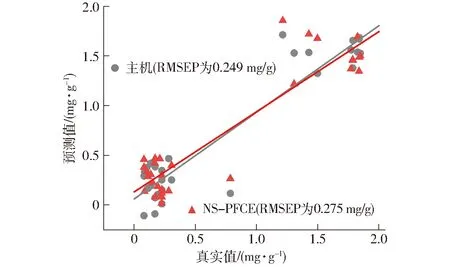
图2 主机与NS-PFCE算法预测食用油酸值散点图

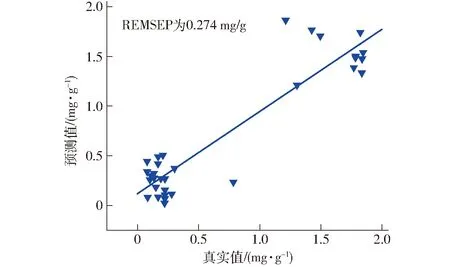
图3 FS-PFCE算法预测食用油酸值散点图

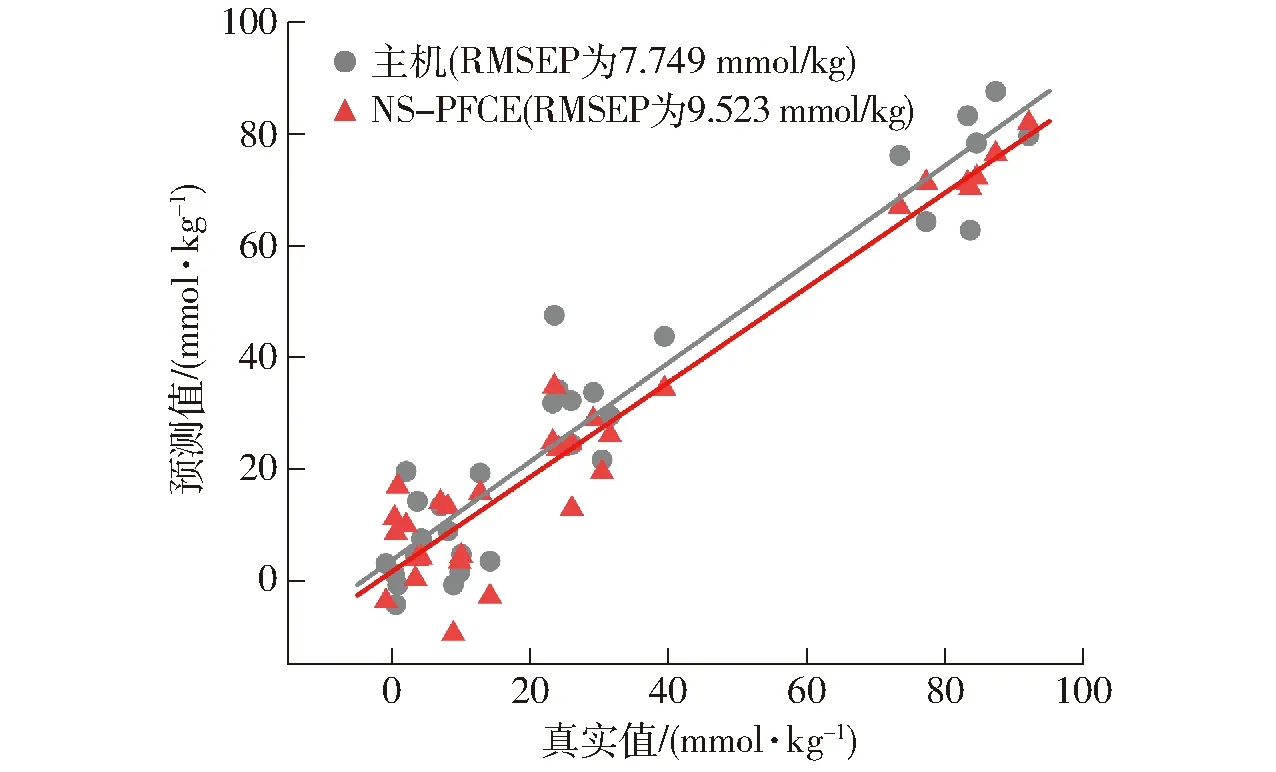
图4 主机与NS-PFCE算法预测食用油过氧化值散点图

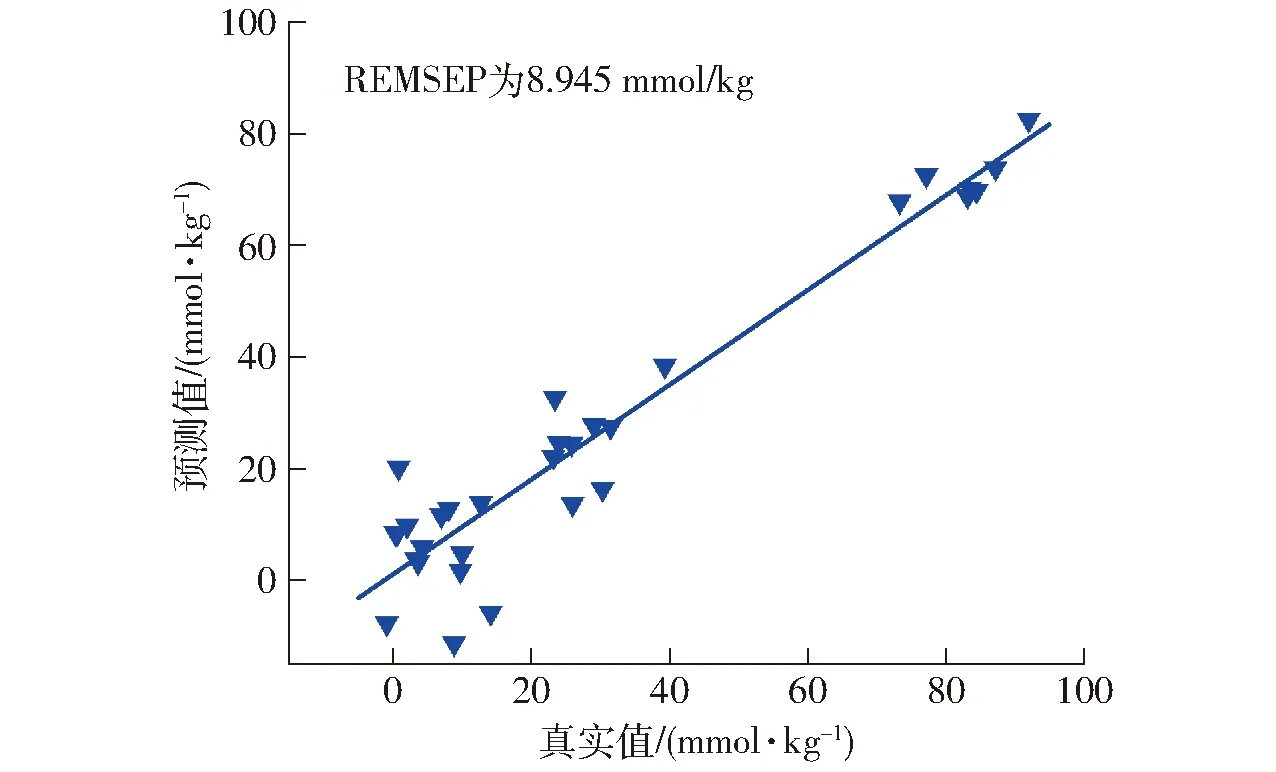
图5 FS-PFCE算法预测食用油过氧化值散点图

食用油酸值与过氧化值建模及预测结果见表5。由表5可知，当从机样品集未进行模型传递直接代入主机模型进行预测时，酸值预测集均方根误差从原先的0.249 mg/g上升到0.613 mg/g，过氧化值预测集均方根误差从原先的7.749 mmol/kg上升到16.153 mmol/kg，预测结果偏差较大，表明从机样本不能直接应用于主机模型，需要对从机样本进行模型传递。

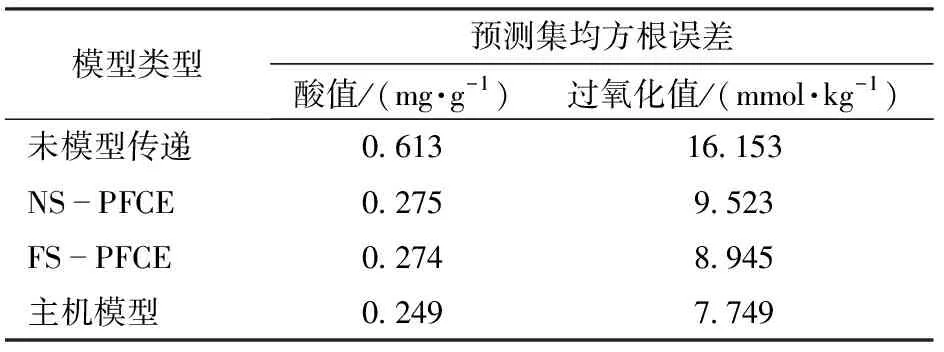
表5 食用油酸值与过氧化值建模及预测结果

分别采用NS-PFCE无标样模型传递算法与FS-PFCE有标样模型传递算法进行传递后，模型预测效果均有明显提升。NS-PFCE算法传递后，酸值的RMSEP下降到0.275 mg/g，过氧化值的RMSEP下降到9.523 mmol/kg。而FS-PFCE算法传递后，酸值的RMSEP下降到0.274 mg/g，过氧化值的RMSEP下降到8.945 mmol/kg。经两种算法传递后的模型预测效果均有所改善，说明PFCE算法使得从机样本能更好地适用于主机模型。且相比之下，FS-PFCE有标样模型传递算法的传递效果优于NS-PFCE无标样模型传递算法，说明有无标准样品成为PFCE算法传递效果的关键。

2.4 标准化样品数目对模型传递的影响

为了进一步探究标准化样品数目对PFCE算法模型传递效果的影响，采用SPXY算法依次从原批次食用油样本的训练集中选取20、40、60、80、100个标准化样品集，食用油酸值与过氧化值建模效果与预测均方根误差如图6所示。

从图6a可知，经NS-PFCE和FS-PFCE算法传递后的酸值预测均方根误差均与训练集标准化样品数目有关，且随着标准化样本数目的增加，预测集均方根误差越小。当标准化样品个数为100时，预测均方根误差达到最小值，经NS-PFCE算法和FS-PFCE算法传递后酸值的RMSEP分别下降到0.283、0.276 mg/g。由图6b可知，经以上两种算法传递后过氧化值预测均方根误差与训练集标准化样品数目呈相同规律，且当标准化样品个数为100时，预测均方根误差也达到最小值，传递后过氧化值RMSEP分别下降到9.498、8.945 mmol/kg。

图6 不同标准化样品数目预测均方根误差

相比之下，经FS-PFCE算法传递后的预测集均方根误差均小于NS-PFCE算法，说明FS-PFCE有标样模型传递算法的传递效果优于NS-PFCE无标样模型传递算法。

2.5 PFCE算法传递效果比较

为了评估PFCE算法的模型传递效果，研究比较S/B、DS和PDS有标样模型传递算法，同时也比较FIR和SCARS无标样模型传递算法。将从机32个样本集分别代入以上经不同算法传递后的校正模型进行预测，4种有标样模型传递算法与3种无标样模型传递算法预测结果如表6、7所示。

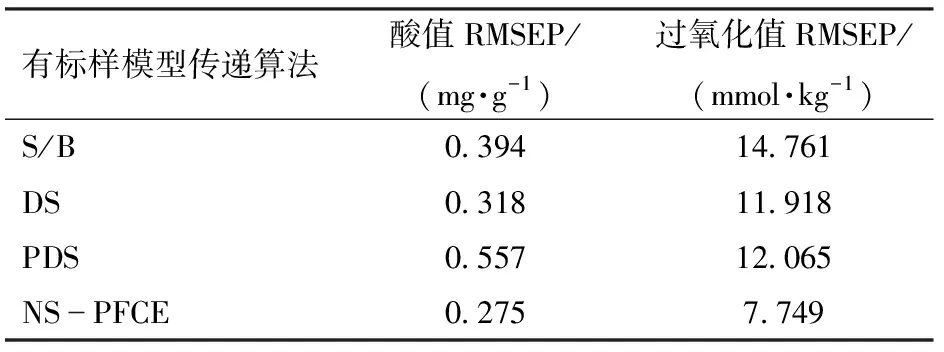
表6 4种有标样模型传递算法酸值与过氧化值模型预测结果

对比4种有标样模型传递算法，均有效地降低酸值和过氧化值预测集均方根误差，提升从机样本对主机模型的适应能力。其中NS-PFCE算法传递效果最优，对比3种无标样模型传递算法，也都有效地降低了酸值和过氧化值预测集均方根误差。FS-PFCE算法传递效果仍是最优。

表7 3种无标样模型传递算法酸值与过氧化值模型预测结果

2.6 讨论

PFCE算法包含无标样模型传递算法和有标样模型传递算法，其传递效果均优于经典有标样和无标样算法，使模型传递算法不再局限于其中一种传递方式，提高了模型传递适用性和包容性。且相比之下，有标样模型传递算法的传递效果优于无标样模型传递算法，说明有无标准样品成为模型传递算法效果的关键。另外，PFCE算法无参数，只需设置相关系数的阈值，模型传递效率高，使得从机样本更接近于主机模型，从而实现了不同仪器间多元校正模型的共享。

3 结论

(1)经NS-PFCE算法传递后的从机样本酸值预测模型RMSEP从0.613 mg/g降低到0.275 mg/g，过氧化值的RMSEP从16.153 mmol/kg降低到9.523 mmol/kg；而FS-PFCE算法传递后的从机样本酸值预测模型的RMSEP降低到0.274 mg/g，过氧化值的RMSEP降低到8.945 mmol/kg。分别对比其余4种有标样模型传递与3种无标样模型传递，PFCE算法的预测效果最优，且FS-PFCE算法均优于NS-PFCE算法。此外，PFCE算法随着标准化样本数目的增加，预测集均方根误差减小。

(2)联合模型传递的有标样传递算法和无标样传递算法，采用PFCE中NS-PFCE无标样算法和FS-PFCE有标样算法分别实现了食用油的酸值与过氧化值在不同仪器间的传递。并与DS、PDS、S/B的有标样算法和FIR、SCARS无标样算法进行对比研究。PFCE算法有效地降低主机与从机之间的光谱差异，提高了从机样本在主机模型的适应度，实现了不同光谱仪间的模型共享。