基于PSO的SURF IA选星优化研究

赵巍巍,段理智,李秀易，简旭红

(1. 中国民航飞行学院 飞行技术学院，四川 广汉 618300；2. 中国民航飞行学院 广汉分院，四川 广汉 618300)

0 引言

随着航班旅客流量逐年递增，在一些繁忙大机场的日常场面运行中，尤其是当航空器驾驶员在低能见度或复杂滑行路线的情境时，运行的风险也随之增加。场面新技术——机场场面情景意识显示和告警(Enhanced Traffic Situational Awareness on the Airport Surface with Indications and Alerts，SURF IA)的运用可以降低运行风险。

SURF IA作为广播式自动相关监视(Automatic Dependent Surveillance-Broadcast IN，ADS-B IN)信息的场面应用之一，通过驾驶舱交通信息显示器(Cockpit Display of Traffic Information，CDTI)向机组提供场面及其附近的其他交通信息，在机场运行的过程中，能够降低跑道侵入和飞机碰撞风险，提高机组情景意识。北斗卫星导航系统(BDS)是我国自主研发的导航系统，是为全球用户提供全天候、全天时、高精度的定位、导航和授时服务的国家重要空间基础设施。美国的GPS源数据可靠且精度高，但是SURF IA技术的精度要求更高。2020年，有研究人员对场面运行SURF IA的可行性进行了分析，单BDS或GPS不能满足运行监视性能要求，而采用GPS+BDS双星座组合系统则满足运行标准[1]。因此，本文采用BDS/GPS组合系统作为ADS-B水平位置信息源。

对于多星座系统，卫星数量的增加会改变卫星的空间布局，提高定位的精度，但在接收更多可见卫星的前提下，也会增加接收机的工作负荷。有鉴于此，在满足精度的条件下，减少使用的卫星数量，将会有效降低接收机工作负荷，且提高卫星的利用率。多年前，国外学者就利用几何精度因子(Geometric Dilution of Precision，GDOP)与多面体体积之间的关系，采用几何法进行卫星的筛选方法研究[2-4]。Mosavi等[5-6]利用群智能算法进行了卫星筛选研究，先后证明了算法的有效性，提高了定位精度。文献[7]通过定义每颗卫星对总GDOP所占的权重，对传统选星算法进行了改进。Teng等[8]严格推导了GDOP公式，研究了增加不同星座的卫星对GDOP的影响。宋丹等[9]使用了遗传算法进行了卫星筛选。徐小钧等[10]研究了多目标遗传算法的选星算法。王尔申等[11-12]针对多星座的卫星筛选采用粒子群算法(Particle Swarm Optimization, PSO)，并进行了一系列的改进，取得了非常好的效果。邱明等[13]使用了基于帝国竞争优化算法(Imperialist Competitive Algorithm, ICA)进行了选星策略的研究，减少了筛选卫星的数目和GDOP值。

本文将PSO创新性地应用于SURF IA中,通过对所有可见卫星进行筛选，验证了可以用更少的卫星满足SURF IA运行要求，筛选后的各关键性能参数符合性达100%，该研究结果有利于提高导航卫星定位的时效性，改善SURF IA场面监视性能。

1 SURF IA监视的最低运行性能标准

ADS-B IN的SURF IA最低运行性能标准中给出了对SURF IA监视质量指标的要求，可用于评估和确定SURF IA运行中的位置和速度信息能否达到规定的精度水平。

监视质量指标分为位置精度指标和速度精度指标，前者为位置导航精度类别(Navigation Accuracy Category for Position，NACp)，后者为速度导航精度类别(Navigation Accuracy Category for Velocity，NACv)。RTCA DO-323[14]中要求实施SURF IA的精度需要满足以下条件：

① SURF IA监视要求为NACp≥9(95%)。其中，指示和告警功能仅在NACp为10或11的情况下使用，则实施SURF IA全部功能位置精度要求为NACp≥10(95%)；

② SURF IA运行时，速度精度为NACv≥1(95%)。其中，95%表示监视质量指标达标概率大于95%，就认为满足监视性能的要求[14-16]。

2 多星座监视参数计算模型

BDS和GPS组合导航系统的定位原理如下：

ρk=rk+c·δG+c·δB(k=1,2,…)，

(1)

式中，ρk为所有的组合卫星中第k颗卫星的测量伪距；rk为组合卫星中第k颗卫星的几何距离；c为无线电信号的传播速度；δG为GPS地面接收机与标准时的钟差；δB为BDS地面接收机与标准时的钟差。通过泰勒定理将非线性方程式(1)展开，得到线性化方程：

HΔX+ε=Δρ，

(2)

式中，ΔX=[Δx,Δy,Δz,δG,δB]T，前3项是地面用户接收机位置与近似位置的偏移分量：ε为伪距测量总误差矢量；Δρ为预测近似值减去测量伪距值的矢量；H(i+j)×5为观测矩阵，即：

(3)

式中，gi=(gxi,gyi,gzi)表示GPS卫星系统中近似用户位置指向第i颗卫星的方向余弦；bj=(bxj,byj,bzj)表示北斗卫星系统中近似用户位置指向第j颗卫星的方向余弦。H是一个(i+j)行5列的矩阵，为了求解方程，必须要求i+j≥5。对式(2)，令b=Δρ-ε，利用最小二乘法求解式(2)得：

ΔX=(HTH)-1HTb。

(4)

dx=[(HTH)-1HT]dρ。

(5)

根据协方差的定义可得：

(6)

(7)

通过比较式(6)和式(7)可以知道，矩阵(HTH)-1各分量定量地表示伪距差如何变换成dx的协方差的各个分量。于是，可以定义权系数矩阵：

G=(HTH)-1。

(8)

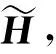
(9)

在BDS/GPS组合系统下的卫星筛选流程，如图1 所示。

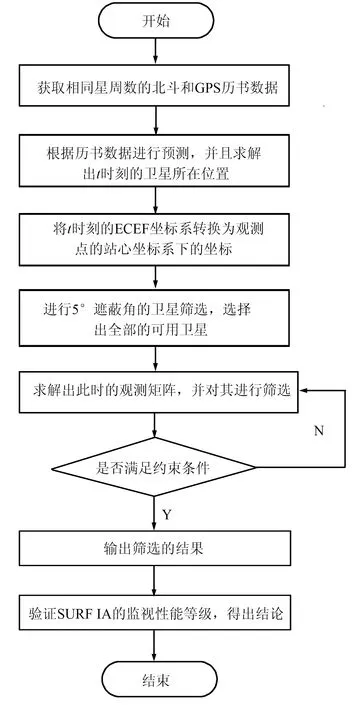
图1 BDS/GPS组合系统的卫星筛选流程Fig.1 Satellite selection flow chart of BDS/GPSintegrated system

3 SURF IA运行性能标准

3.1 监视精度要求

随着导航卫星定位精度的不断提升，在实际计算过程中，一般计算求解出的NACp≥7，而NACp编码是基于位置估计不确定度(Estimate of Position Uncertainty，EPU)确定的。EPU表示的是以ADS-B的报告位置为圆心，EPU为半径的圆，航空器的实际水平位置有95%的概率在该圆的区域内，即用户接收机解算位置与实际位置的偏差范围。当由GPS或GNSS系统报告导航信息时，EPU也被称为水平品质因数(Horizontal Figure of Merit，HFOM)。RTCA DO-323对实施SURF IA的监视精度要求有严格的规定[14-16]，具体如表1和表2所示。

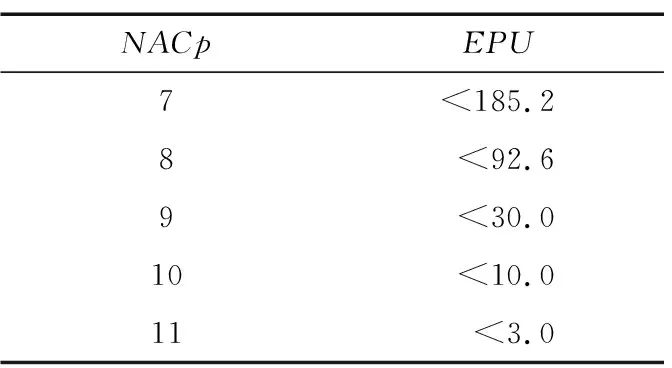
表1 位置导航精度类别Tab.1 Navigation accuracy category for position 单位：m

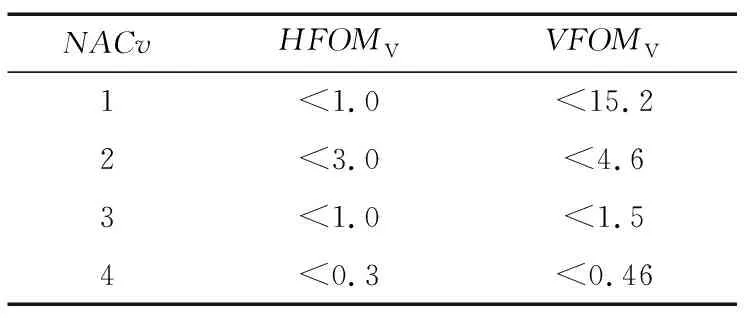
表2 速度导航精度类别Tab.2 Navigation accuracy category for velocity 单位：m/s

3.2 多星座定位精度

导航定位精度主要由卫星布局或测量误差影响，精度因子(Dilution of Precision, DOP)反映了可见卫星与接收机空间几何结构对用户测距误差的放大作用[17]，DOP与定位精度成反比，DOP越小，卫星布局越好，定位精度越高。根据DOP的定义可以得到：

(10)

根据定义可得EPU=HFOM=2·HDOP·σURE，由RTCA DO-242中定义的位置精度与速度精度可以得到SURF IA运行监视相关参数：

(11)

式中，f为比例因子；aH和aV为加速度因子；T为传感器接收时间；σURE值为空间信号用户测距误差。通常情况下，它们的取值为f=0.02 s-1，aH=aV=1 m/s2，T=1 s，σURE=5。根据HFOMV，VFOMV可在表2中找出对应的NACV值。

性能精度指标均基于FOM值，根据上述算法，FOM与DOP紧密相关且成正比。多星座导航系统增加了卫星数，DOP值随之减小，得到的FOM值也随之减小，参照编码规则可得的监视性能精度指标NACv，NACp增大，则能够获得相对更优的监视性能。根据现有的规则可以得到相应的监视等级。对所有可见卫星进行数据分析可以得到相关性能参数，如表3所示。

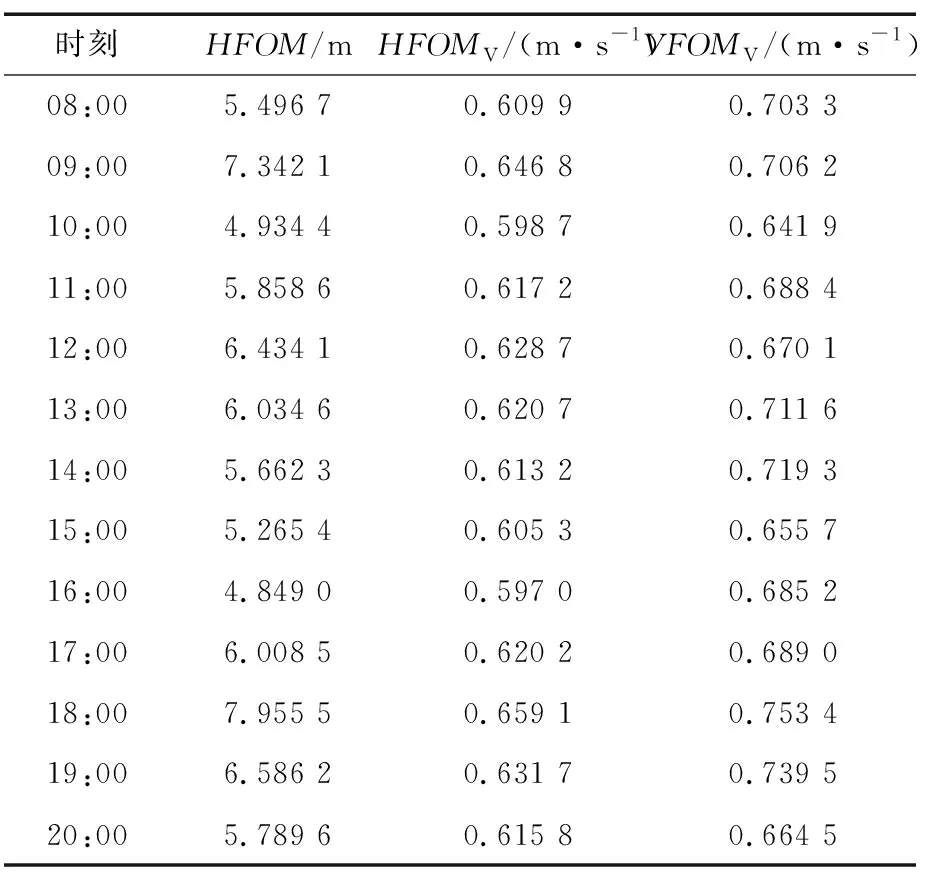
表3 使用所有可见卫星后的监视参数Tab.3 Monitoring parameters after using all visible satellites

使用GPS和BDS的所有可见卫星时，参照表1～表3可知，位置导航精度类别最高能达到NACp10，速度导航精度类别最高能达到NACv3。

4 基于PSO的卫星筛选

4.1 PSO

PSO[18-19]的灵感来自于鸟群捕食行为，在PSO中每一个寻优问题解都被想象成一只鸟，称为“粒子”，算法的初始化是生成一群随机粒子(随机解),每个粒子可视为N维搜索空间中的一个搜索个体，粒子的当前位置即为对应优化问题的一个候选解，粒子的飞行过程即为该个体的搜索过程，粒子的飞行速度可根据粒子历史最优位置和种群历史最优位置进行动态调整。速度和位置是粒子的2个属性，速度代表移动的快慢，位置代表移动的方向。每个粒子单独搜寻的最优解叫做个体极值，粒子群中最优的个体极值作为当前全局最优解。不断迭代，更新速度和位置，得到满足终止条件的最优解。更新速度和位置的公式如下：

Vid(t+1)=wVid(t)+C1random(0,1)(Pid-Xid)+

C2random(0,1)(Pgd-Xid),

(12)

Xid(t+1)=Xid(t)+V(t+1),

(13)

式中，Vid为粒子的速度；t为当前迭代次数；w为惯性加权因子；random为0～1的随机数，用来增加搜索随机性；Pid为每个粒子历史最佳位置；Pgd为群体中所有粒子的最佳位置；Xid为粒子的位置；加速度常数C1≥0且C2≥0，称为学习因子，调节学习最大步长。

4.2 组合卫星筛选模型

本文在BDS和GPS组合导航卫星系统中，通过PSO进行卫星筛选，以GDOP值最小为目标，根据式(10)和矩阵的迹可以得到如下的目标函数：

(14)

式(14)由式(9)得到，相应的约束条件如下：

(15)

式中，第1个约束条件表示满足卫星的可用性，即PDOP<6；第2个和第3个约束条件表示由前面的表3结果，使用SURF IA监视性能中的NACp10和NACv3作为筛选的标准；第4个约束条件表示未知量的求解需要至少5颗导航定位卫星，total表示所有观测到的导航卫星数量；Z为整数集合。

由于不同时刻下得到的H矩阵不同，粒子位置可由一组小于当前H矩阵最大维数的数组作为参数，式(9)可作为适应度函数，基于PSO算法的SURF IA选星步骤如下：

① 初始粒子群信息。设置种群规模为20个，迭代次数为100，惯性权重为0.9，加速度因子C1和C2都设为1.494 45，粒子的初始位置可随机产生。

② 由适应度函数计算粒子的适应度值，记录每个粒子历史最佳位置Pid以及群体中所有粒子发现的最佳位置Pgd。

③ 由式(7)和式(8)更新每个粒子的速度与位置。

④ 重复步骤②，计算粒子的适应度，更新历史最佳位置以及群体粒子中的最佳位置。

⑤ 满足约束条件，且达到最大迭代次数后停止计算。

5 仿真分析

5.1 PSO筛选后结果

本文选用BDS801周和GPS109周的BDS和GPS历书数据作为预测仿真的数据源。观测参考点为上海浦东机场的机场参考点(Airport Reference Point，ARP)，预测时长总计12 h、时间间隔1 h、起始时刻为2021-05-13T08:00:00(北京时间)。筛选前后的GDOP结果如图2所示。

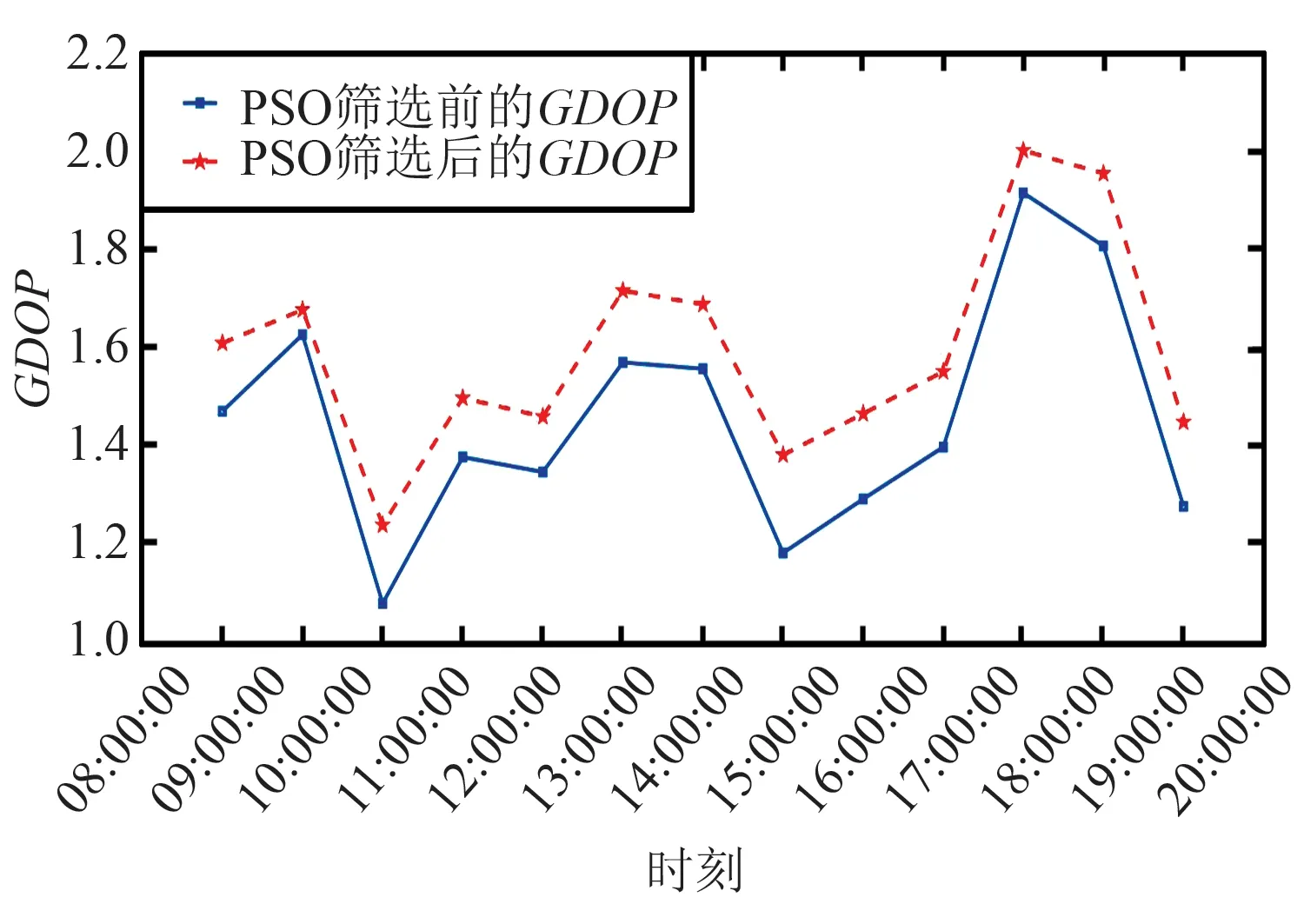
图2 采用PSO筛选前后的GDOPFig.2 GDOP before and after PSO selection

GDOP值可以反映用户和可见卫星在空间几何分布的好坏，采用PSO对所有可见卫星进行筛选，经过筛选后的GDOP值跟筛选前的结果相当。筛选前后的可见卫星数量如图3所示。

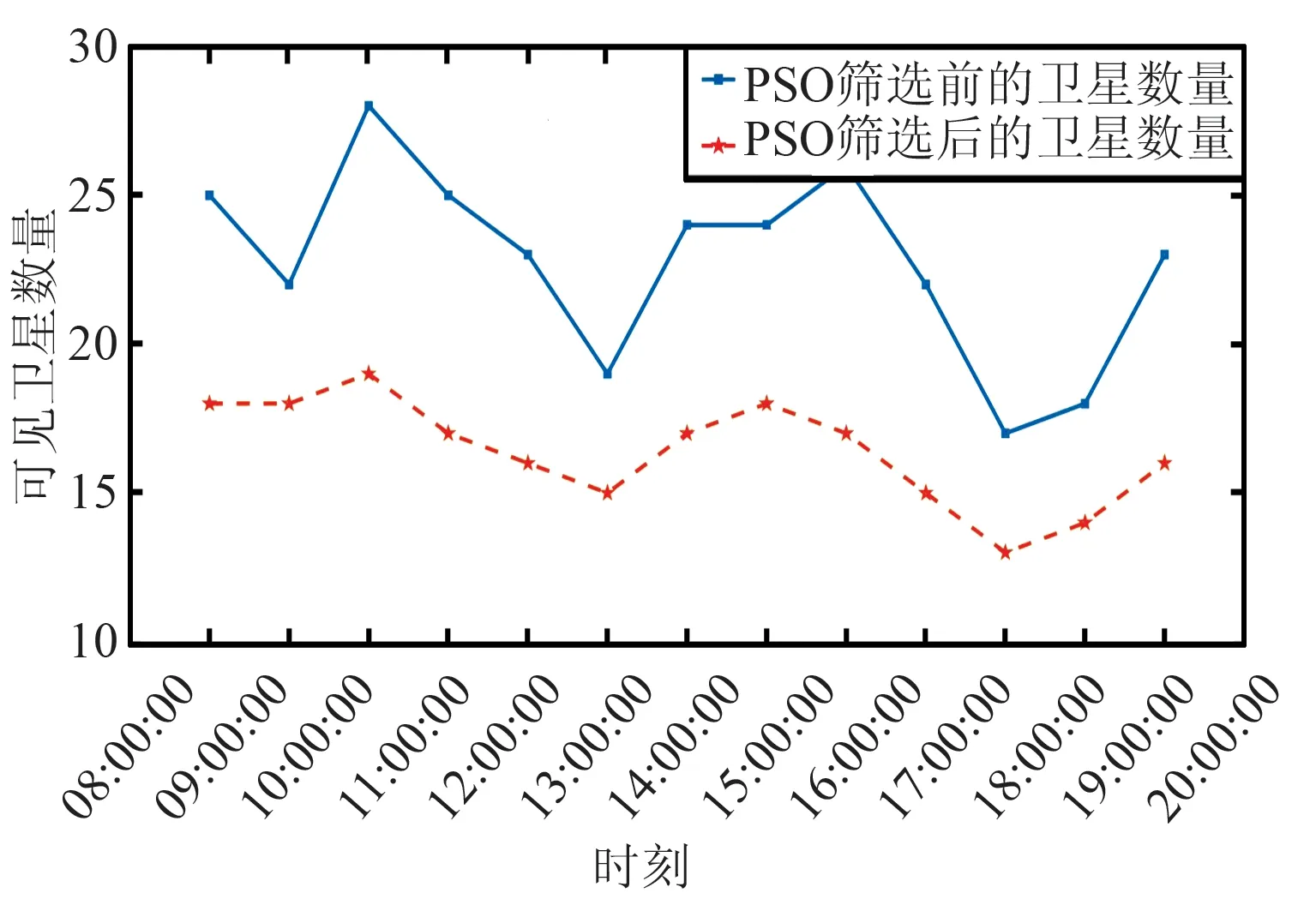
图3 采用PSO筛选前后的可见卫星数量Fig.3 Number of visible satellites before and after PSO selection

由图3可以看出，PSO进行筛选后,卫星数量平均每时刻减少6颗，减少的平均比例为28%；筛选后的卫星计算出的GDOP值比使用所有可见卫星的GDOP值大，是因为卫星数量的减少使得卫星布局劣于所有卫星可见时的布局。

5.2 筛选卫星后的SURF IA性能验证

根据水平精度因子和垂直精度因子，得出SURRF IA场面运行监视性能参数，观测点在12 h预测时间内的HFOM的统计结果如图4所示。观测点在12 h预测时间内的NACV性能仿真验证结果如图5、图6、表4和表5所示。

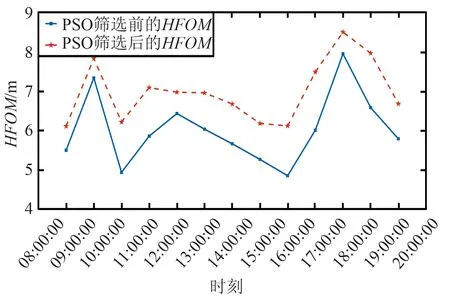
图4 筛选后的HFOMFig.4 HFOM after selection

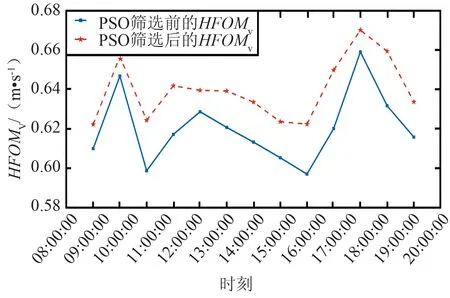
图5 筛选后的HFOMVFig.5 HFOMV after selection

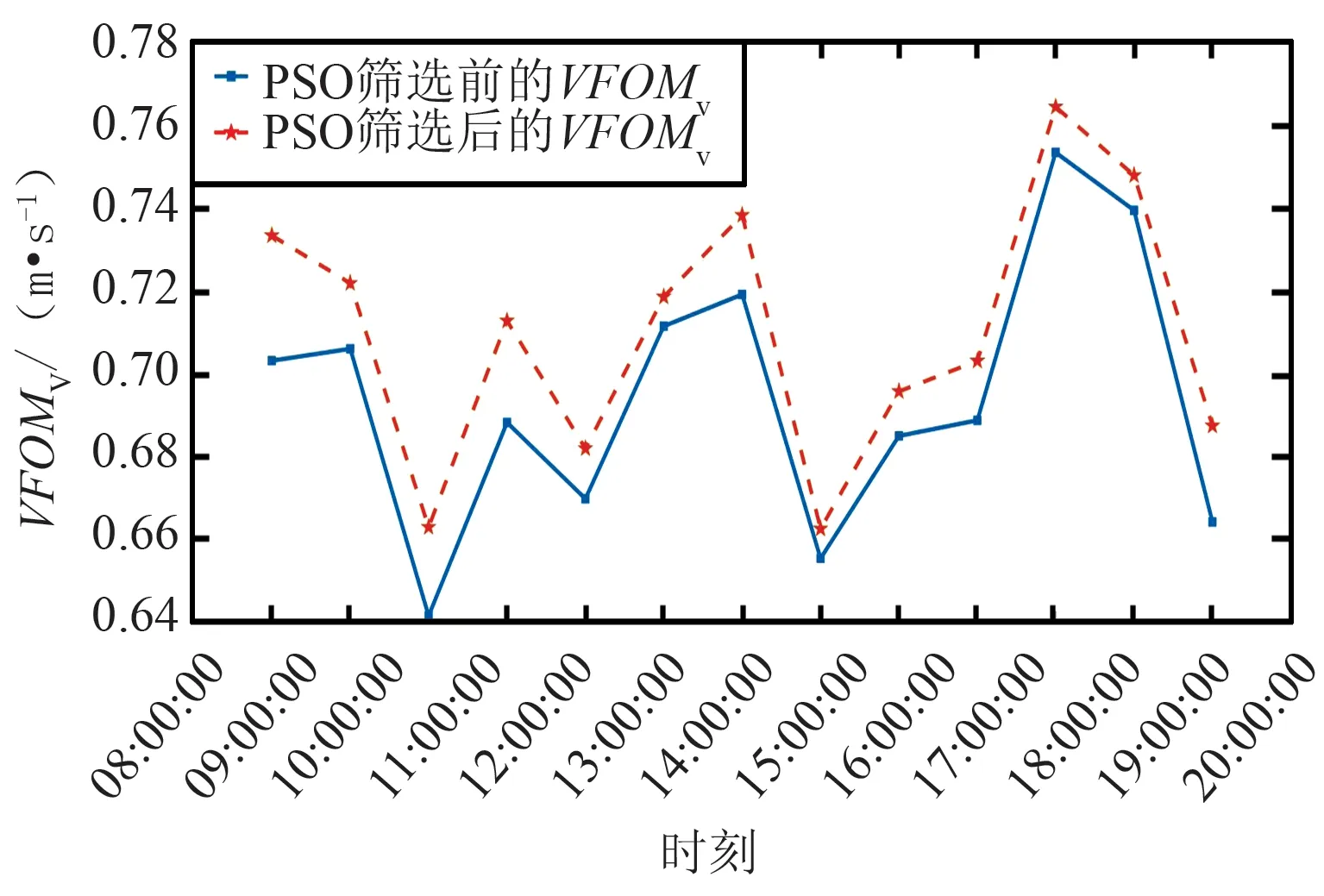
图6 筛选后的VFOMVFig.6 VFOMV after selection

表4 GPS+BDS的NACp性能等级Tab.4 NACp performance level of GPS+BDS

表5 GPS+BDS的NACV性能等级Tab.5 NACV performance level of GPS+BDS

由图4可以看出，HFOM的数值小于10 m。由表4可以看出，GPS+BDS的NACp性能等级达到10级。由图5和图6可以看出，HFOMV的数值均小于1 m/s，VFOMV的数值均小于1.5 m/s，GPS+BDS的NACV性能等级满足3级。

通过以上检验分析可以看出，经过筛选后的卫星，数量平均减少28%，并且定位精度与全部可见卫星相当，可以满足SURF IA监视运行的要求。

6 结束语

基于ADS-B IN的SURF IA监视运行新技术在复杂场面和低能见度场面滑行有着巨大的应用前景，从本文分析结果来看，基于GPS/BDS等多星座组合，采用PSO筛选后的卫星数量相比于当前时刻的可见卫星平均减少28%，同时，计算筛选后卫星的GDOP值，依然可以满足SURF IA运行监视性能的要求。HFOM和VFOM经过验证后，NACp和NACv等级分别达到10级和3级的要求，满足SURF IA运行监视性能要求的标准。本文通过卫星筛选，以更少的卫星数量满足SURF IA运行监视性能要求，为提高卫星定位解算效率提供了方法，对工程应用有重要的意义。