基于迭代更新的SIFT遥感图像配准算法

杨 毅，李大成，于 杰，韩启金

(1.太原理工大学 光电工程学院，山西 太原 030024; 2.太原理工大学 矿业工程学院，山西 太原 030024; 3.中国资源卫星应用中心，北京 100094)

0 引言

图像配准是通过一定的方法获得基准图像与待配准图像之间的映射关系实现图像的几何校准，是诸多遥感应用(如图像融合[1-2]和变化检测[3-4]等)的关键前置环节，对系统性能有着举足轻重的影响。图像配准方法大致可以分为2大类：基于区域的配准方法和基于特征的配准方法。其中，基于区域的配准方法[5-8]一般采用模板匹配策略，利用图像灰度信息寻找基准图像和待配准图像中的同名点实现图像配准。这类方法存在计算量大，对图像旋转、缩放等仿射变换鲁棒性较差的问题。基于特征的配准方法首先在基准图像和待配准图像上提取局部特征点，之后使用图像局部特征描述方法对局部特征进行描述，接着根据一定的评价准则如欧拉距离寻找同名点，最后根据同名点计算基准图像与待配准图像之间的映射关系实现图像配准。与基于区域的配准方法相比，这类方法的计算量更小，对图像旋转、缩放等仿射变换有更好的鲁棒性。例如，Lowe[9]于1999年提出并于2004年完善的尺度不变特征变换(Scale-Invariant Feature Transform，SIFT)算法，该算法通过构建高斯差分金字塔提取多尺度图像局部特征点，建立局部特征点支持区域的三维梯度直方图完成对图像局部特征的描述，使用欧拉距离作为准则寻找同名点。由于SIFT在提取图像局部特征时考虑了多尺度问题，因此在自然图像配准场景中(如图像缩放、旋转)表现出了良好的性能和鲁棒性。之后出现了很多SIFT的变种[10-13]，如Mikolajczyk等[10]使用对数极坐标系替换SIFT算法中使用的笛卡尔坐标系，进一步提升了图像局部特征描述方法的鲁棒性。Bay等[11]使用积分图像和箱式滤波器提高了算法的运行速度和配准精度。

由于SIFT算法在自然图像配准中展示出优良的性能，开始被引入遥感图像配准领域，衍生出多个适用于遥感图像配准场景的变种[14-18]。如Dellinger等[15]为降低合成孔径雷达(Synthetic Aperture Radar，SAR)图像斑点噪声的影响，在SIFT算法基础上改变梯度计算方法提出了SAR-SIFT用于SAR图像配准。Sedaghat等[16]于2011年在SIFT的基础上提出了UR-SIFT算法，该算法通过改变SIFT提取特征点的策略，使特征点在图像中的分布更加均匀，提高了遥感图像配准的精度。

遥感图像中全色图像通常是覆盖整个可见光波段(380～780 nm)的混合图像，多光谱图像是对多个单波段单独成像，获取相应波段的光谱信息。因此，全色图像与多光谱图像之间辐射差异并不是线性关系，造成相似的图像局部特征点在不同波段图像中占据比例和可重复性降低，使得图像局部特征的误匹配率上升，最终导致图像配准质量和精度下降。通过SIFT算法进行全色图像与多光谱图像配准时，由于不同波段遥感图像之间存在复杂辐射差异，使用SIFT算法进行图像配准时无法保证配准质量。因此，本文提出一种基于迭代更新策略的SIFT算法变种，该算法通过遍历基准图像与待配准图像之间的同名点对，迭代求解基准图像与待配准图像之间的映射关系(即单应性矩阵)，得到最优单应性矩阵，对待配准图像进行重采样完成图像配准。

1 本文方法

基于特征的遥感图像配准方法实施图像配准的一般流程是：① 在基准图像和待配准图像上检测并提取图像局部特征；② 通过图像局部特征描述方法对图像局部特征进行描述，使用一定准则寻找同名点；③ 根据同名点计算得出基准图像与待配准图像之间的映射关系，对待配准图像进行重采样完成图像配准。其中，通过基准图像与待配准图像间的同名点对计算单应性矩阵时，同名点对会直接影响单应性矩阵求解的质量，进而影响图像配准精度。本文提出一种迭代更新策略的SIFT算法，该算法的核心是通过遍历基准图像与待配准图像之间的同名点对，迭代求解单应性矩阵，得到最优单应性矩阵，根据单应性矩阵对待配准图像进行重采样完成图像配准，算法流程如图1所示。

图1 本文算法流程Fig.1 Flowchart of the proposed method

2 单应性矩阵质量评价

根据基准图像和待配准图像之间同名点对计算获得的单应性矩阵的质量直接影响图像配准的精度和效果，本文采用同名点对的RMSE作为单应性矩阵质量评价指标。为计算同名点的RMSE，首先使用单应性矩阵H计算待配准图像中的局部特征点xw和yw在基准图像中的坐标xb′=H·xw和yb′=H·yw，接着根据式(1)和式(2)分别计算其与SIFT算法确定的同名点坐标在xb和yb方向的残差Vx和Vy。之后根据式(3)和式(4)计算xb和yb方向的均方根误差mx和my，其中n代表特征点的数量。最后根据式(5)计算得到同名点之间的RMSE(x,y)。同名点集中的每对同名点均通过以上步骤获得其RMSE，RMSE值越小单应性矩阵质量越好。

(1)

(2)

(3)

(4)

(5)

3 实验及结果分析

为验证所提算法的有效性和鲁棒性，在网通一号卫星和高分二号某地区的遥感影像数据上进行了图像配准实验。用于图像配准实验的网通遥感图像如图2所示。

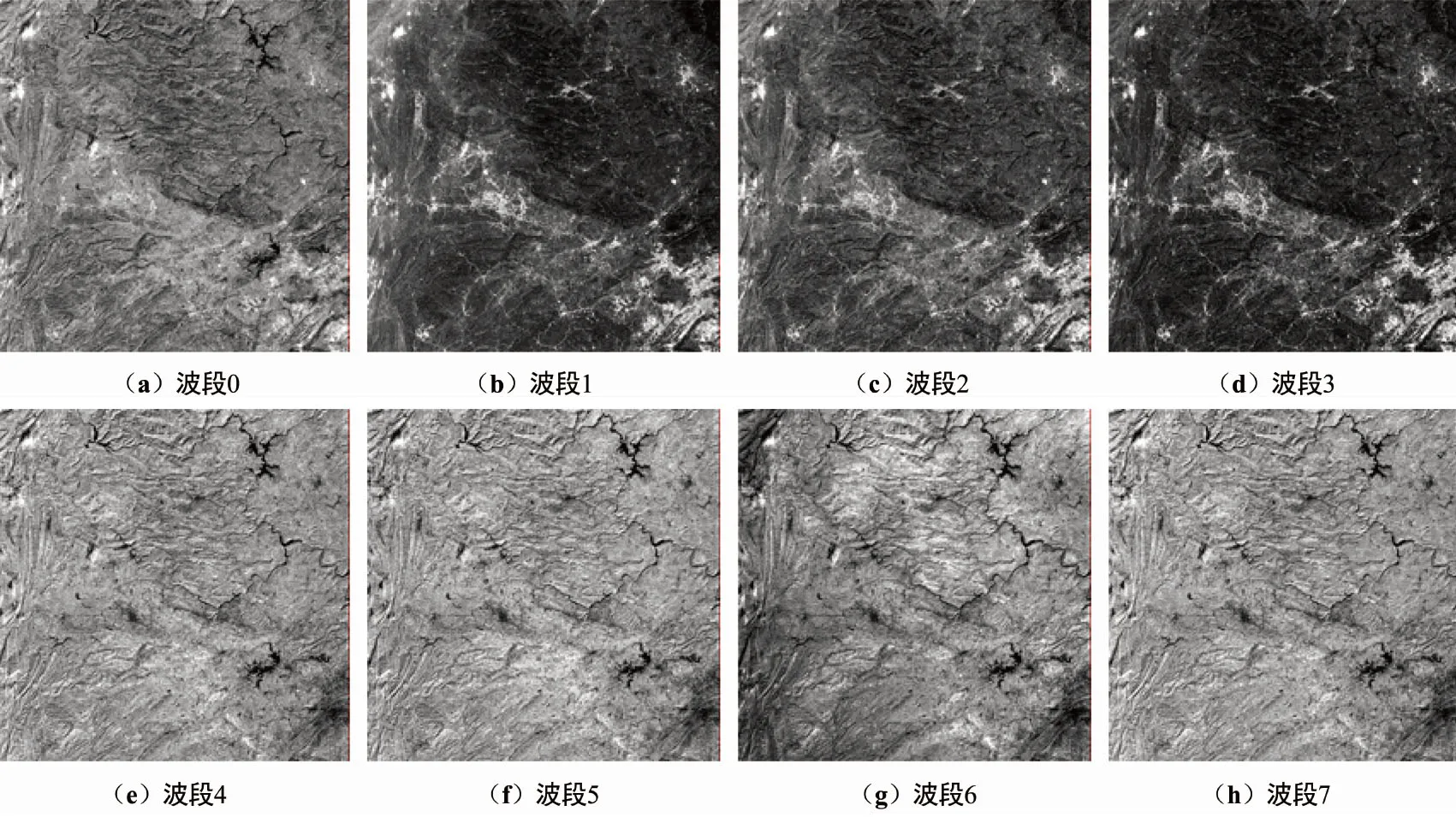
图2 网通卫星图像Fig.2 Images of WT satellite

这一景图像共有8个波段，其中波段0的影像为12 000 pixel×12 000 pixel的全色图像，其余波段影像为3 000 pixel×3 000 pixel的多光谱图像。

高分二号某地区遥感图像如图3所示，其中全色图像尺寸为29 200 pixel×27 620 pixel，多光谱图像尺寸为7 300 pixel×6 908 pixel，限于篇幅本文取全色图像及其多光谱图像的波段1～3用于图像配准实验。从图2和图3所示的遥感图像可以看出，全色图像和多光谱图像之间不仅仅是分辨率不同，还存在复杂的辐射差异，造成不同波段的图像存在明显且非线性的灰度变化。

图3 高分二号卫星图像Fig.3 Images of GF-2 satellite

本文在Windows 10系统上基于QT64位开发平台，结合GDAL(Geospatial Data Abstraction Library)和OpenCV开源库搭建了遥感图像配准实验环境。由于遥感图像的位深是16 bit，在进行图像配准实验前采用最大值最小值拉伸算法将遥感图像位深转换为8 bit以方便之后实验。

首先验证基于迭代更新策略的SIFT算法获取基准图像与待配准图像之间最优映射关系的有效性。通过SIFT算法分别从基准图像和待配准图像提取1 000个特征点，接着使用欧拉距离作为评价准则，确定基准图像和待配准图像之间的同名点。由于SIFT算法完成粗匹配后可能会存在误匹配点，在计算基准图像与待配准图像间的单应性矩阵前使用RANSAC算法对同名点进行初步提纯。首先以网通卫星影像波段0作为基准图像，其他波段1～7作为待配准图像进行实验。限于篇幅，仅呈现波段0与波段1、波段0与波段2、波段0与波段4、波段0与波段7的实验结果，如图4～图7所示。

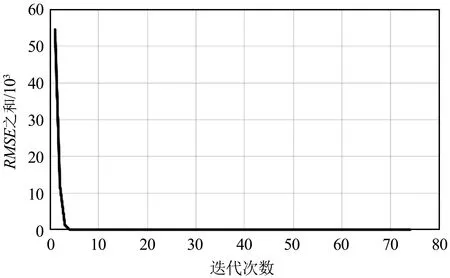
(a)整体实验结果

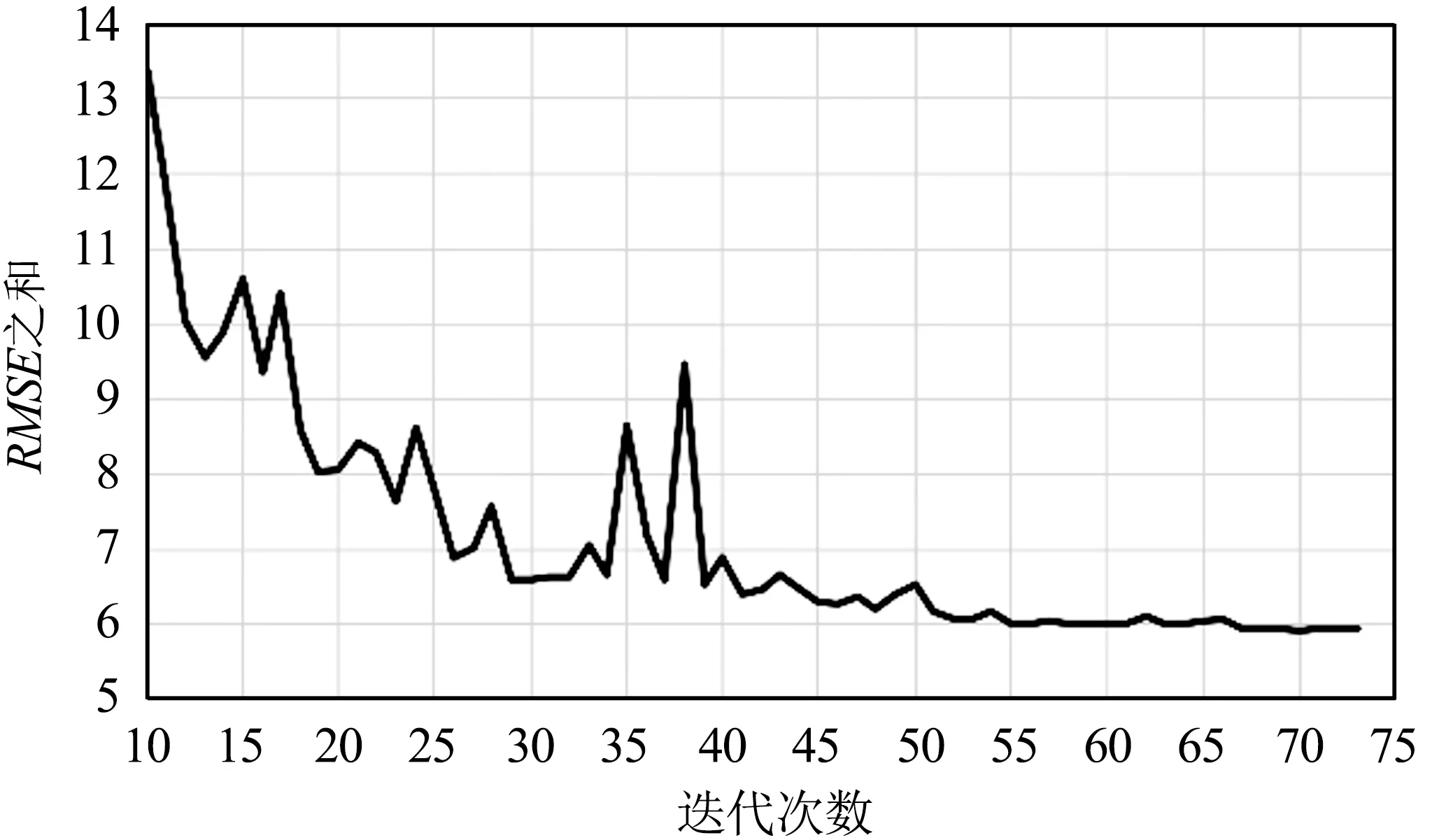
(b)迭代次数10～74的结果图4 波段0与波段1的RSME之和与迭代次数的实验结果Fig.4 Experimental results of the sum of RMSE and number of iterations for bands 0 and 1

(a)整体实验结果

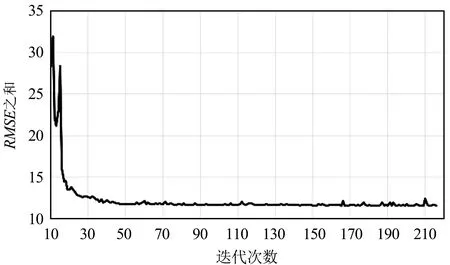
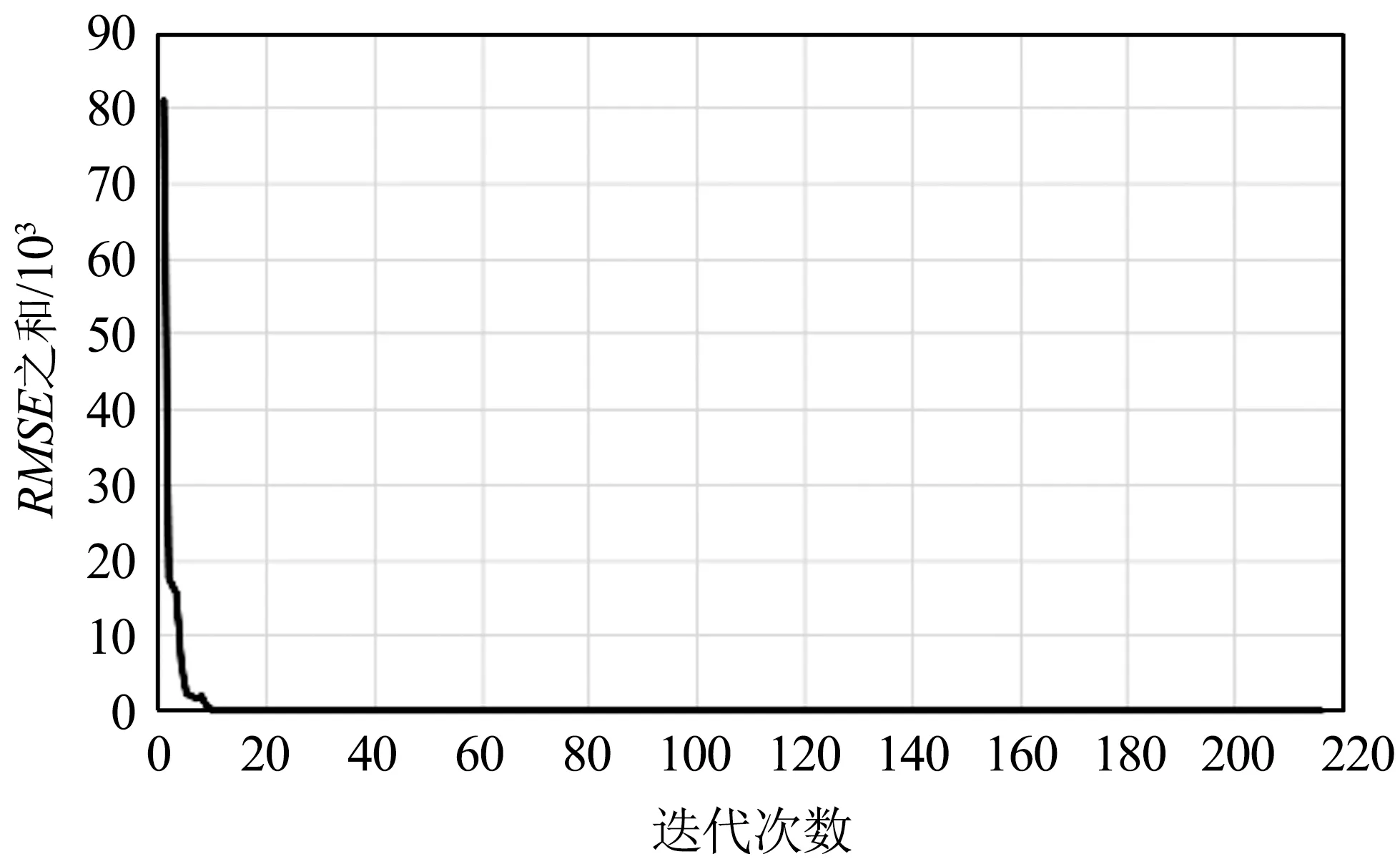
(b)迭代次数10～216的结果图5 波段0与波段2的RSME之和与迭代次数的实验结果Fig.5 Experimental results of the sum of RMSE and number of iterations for the bands 0 and 2

(a)整体实验结果

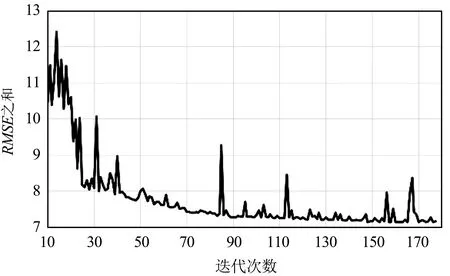
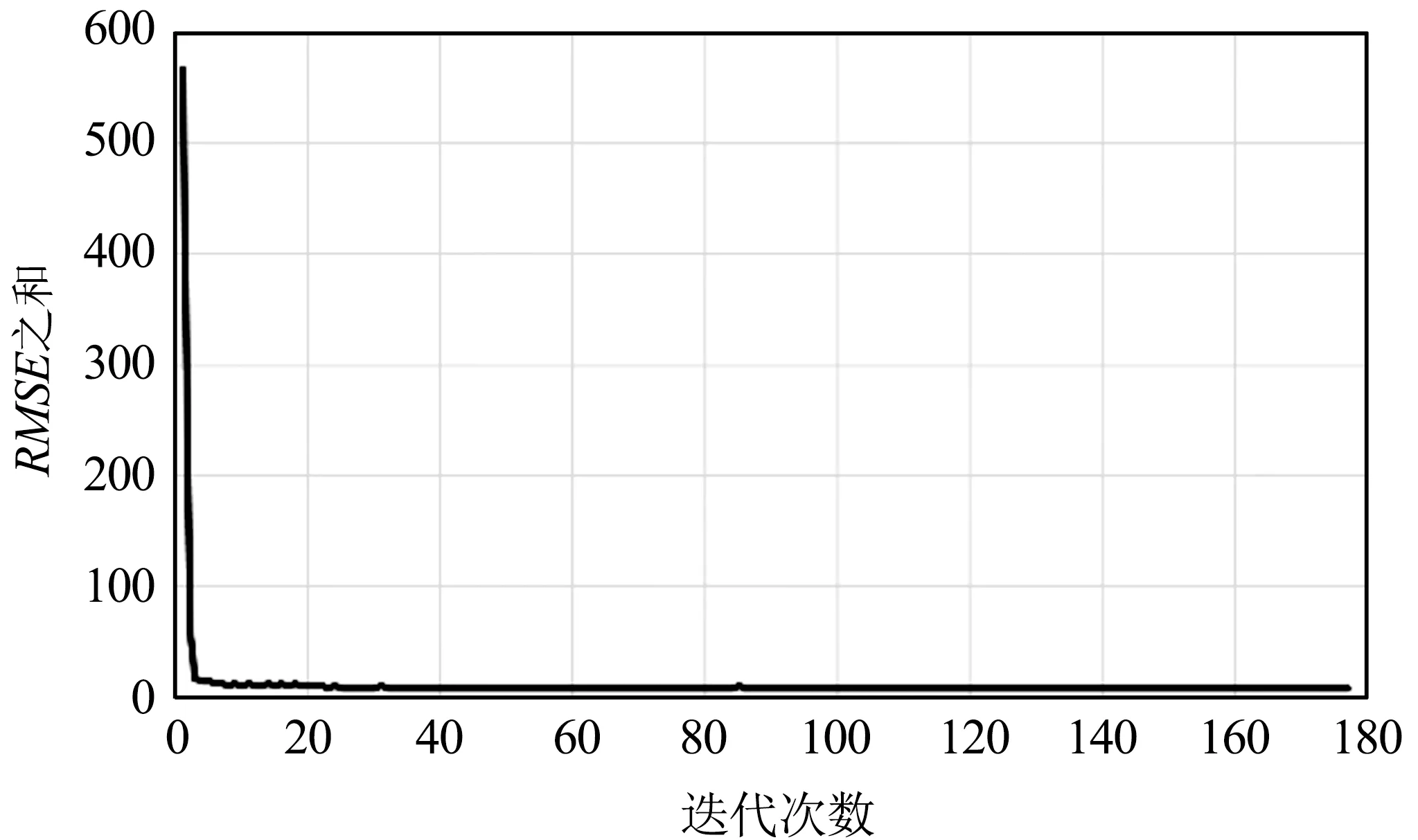
(b)迭代次数10～177的结果图6 波段0与波段4的RSME之和与迭代次数的实验结果Fig.6 Experimental results of the sum of RMSE and number of iterations for the bands 0 and 4

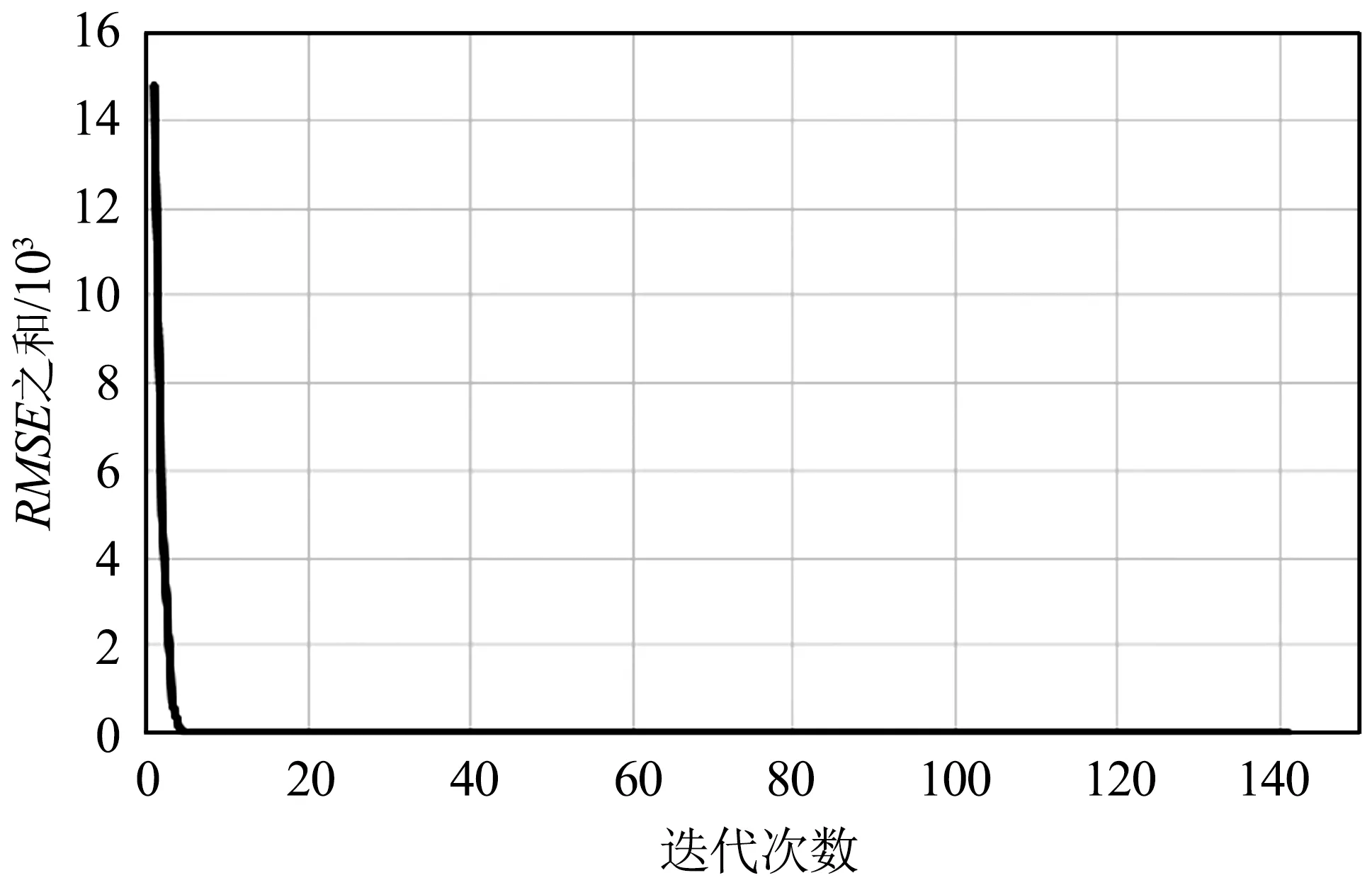
(a)整体实验结果

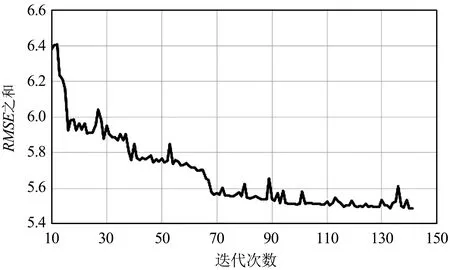
(b)迭代次数10～141的结果图7 波段0与波段7的RSME之和与迭代次数的实验结果Fig.7 Experimental results of the sum of RMSE and number of iterations for bands 0 and 7

接着，本文以高分二号全色图像作为基准图像，多光谱波段1～3作为待配准图像进行了图像配准实验，实验结果如图8～图10所示。

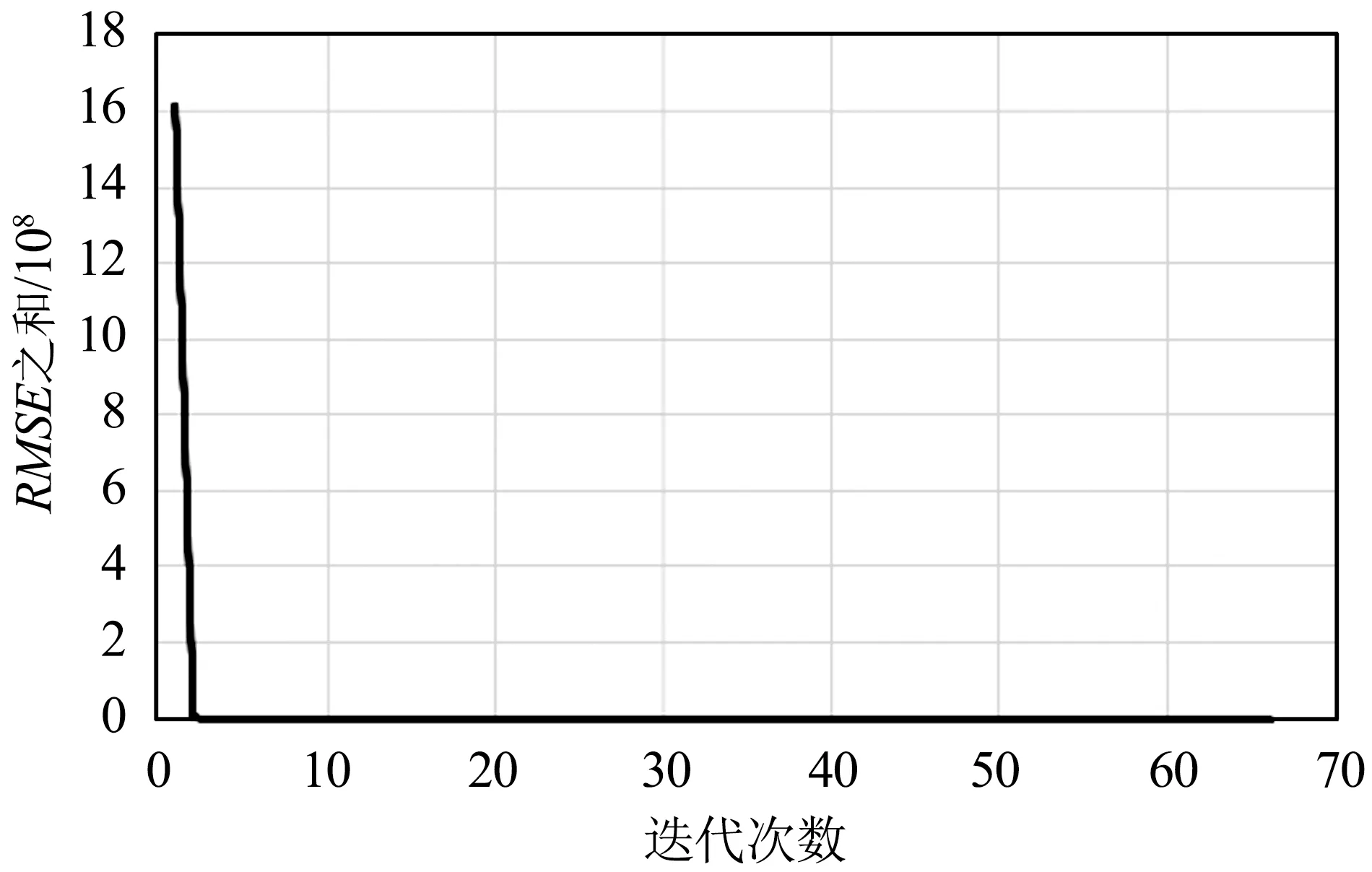
(a)整体实验结果

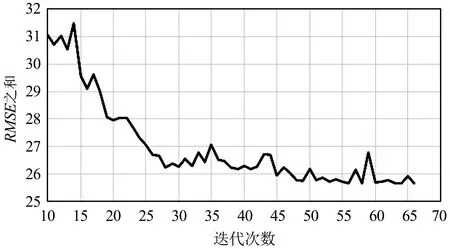
(b)迭代次数10～66的结果图8 全色图像与多光谱波段1的RSME之和与迭代次数的实验结果Fig.8 Experimental results of the sum of RMSE and number of iterations for panchromatic image and multi-spectral band 1

(a)整体实验结果

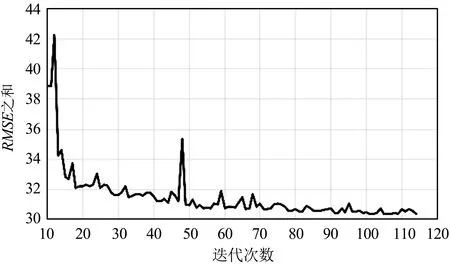
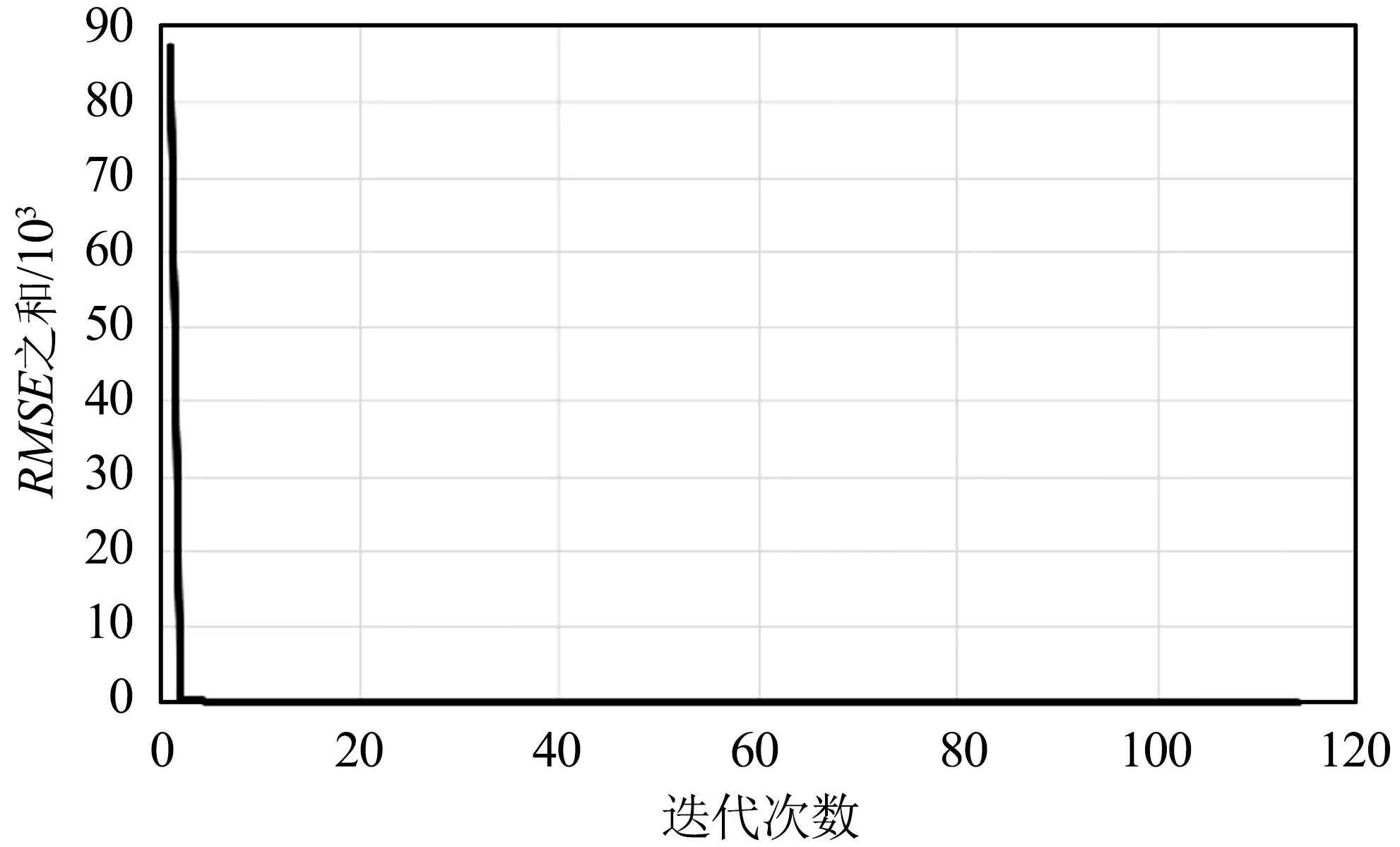
(b)迭代次数10～114的结果图9 全色图像与多光谱波段2的RSME之和与迭代次数的实验结果Fig.9 Experimental results of the sum of RMSE and number of iterations for panchromatic image and multi-spectral band 2

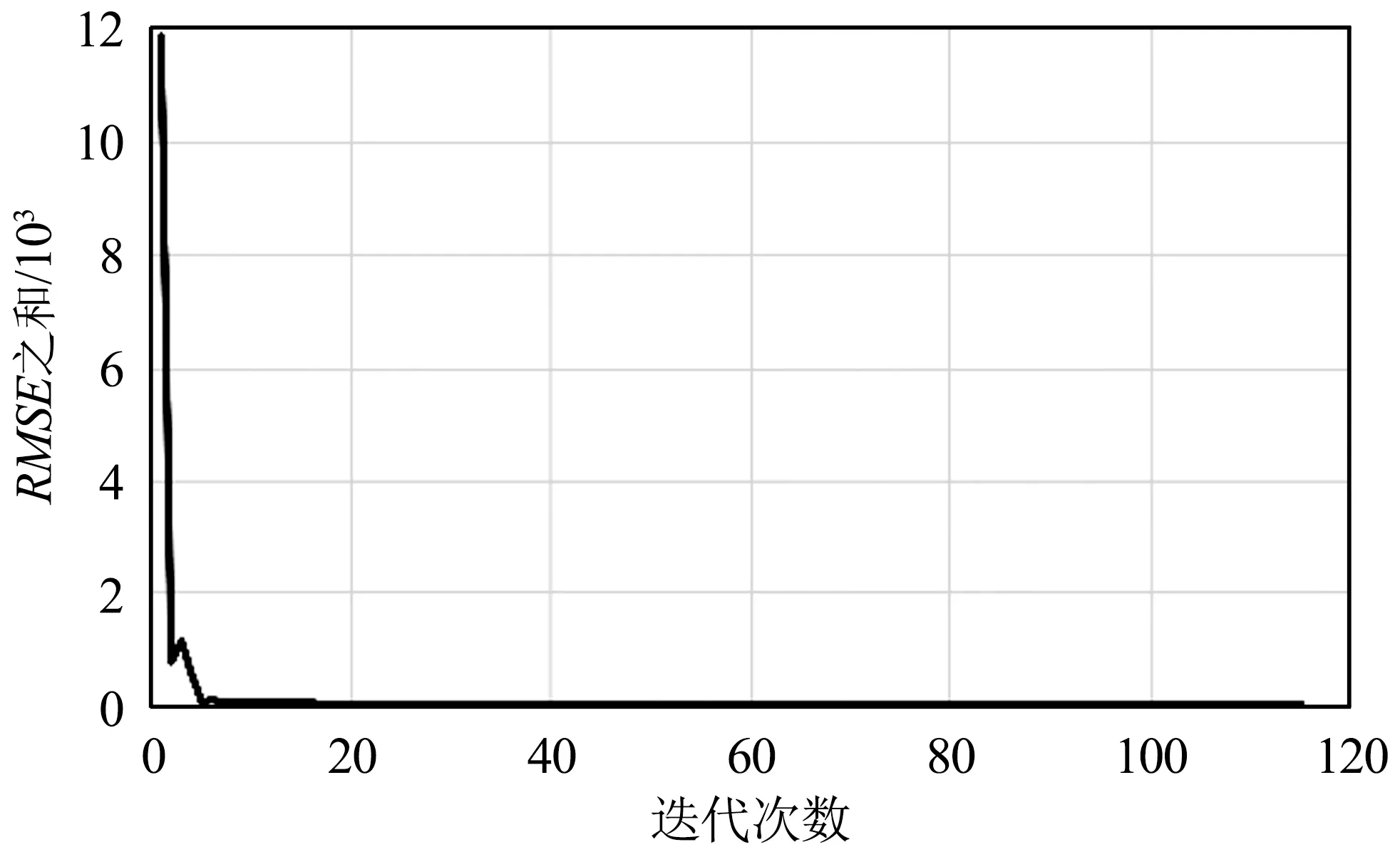
(a)整体实验结果

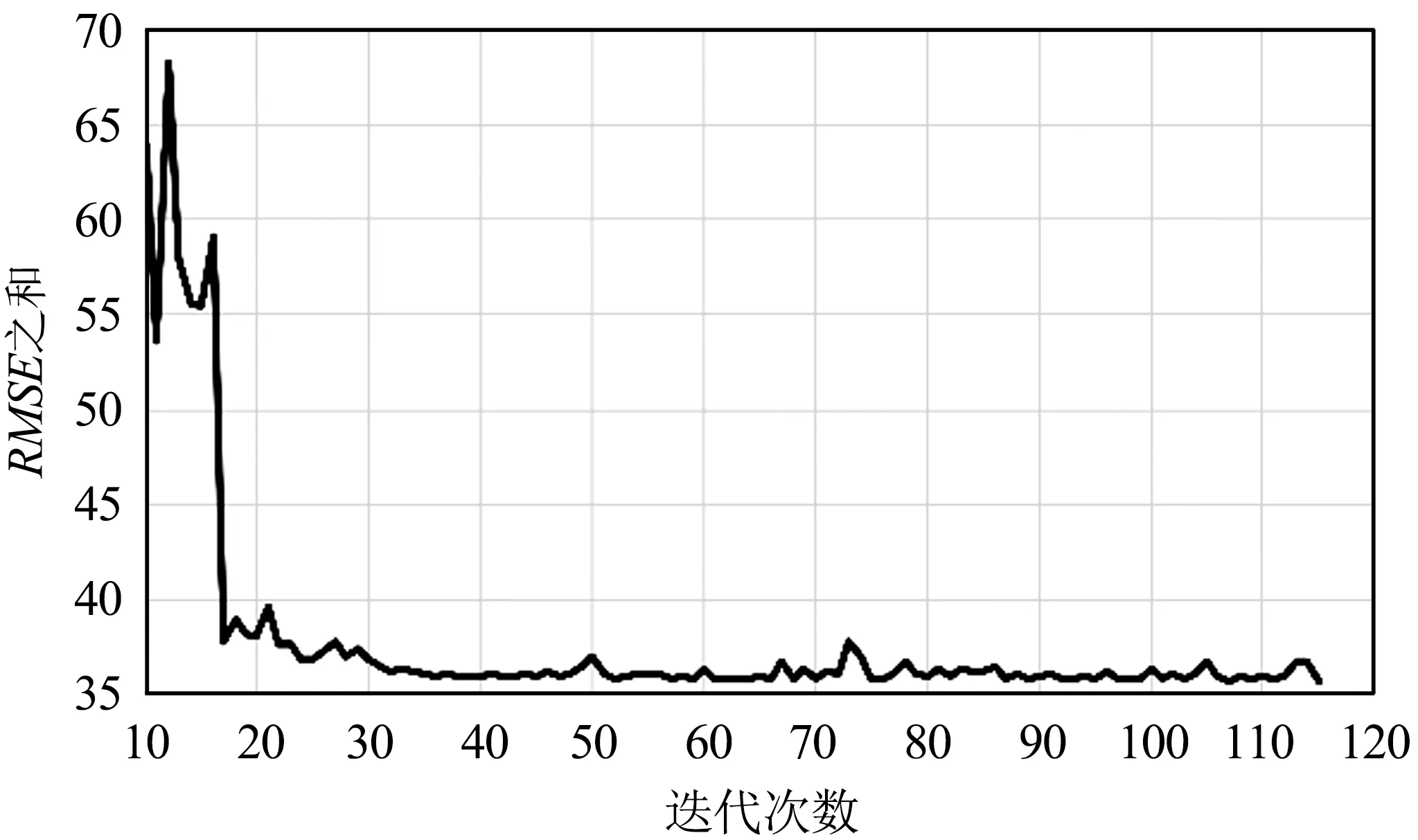
(b)迭代次数10～115的结果图10 全色图像与多光谱波段3的RSME之和与迭代次数的实验结果Fig.10 Experimental results of the sum of RMSE and number of iterations for panchromatic image and multi-spectral band 3

从图4～图10可以看出，迭代策略刚开始阶段RMSE之和会有非常明显的下降，说明同名点对的数量对求取基准图像与待配准图像之间的映射关系有非常大的影响。换句话说，虽然基准图像和待配准图像间的单应性矩阵仅有8个自由变量，理论上4对同名点便可将8个自由变量全部求解出来，但此时获得的单应性矩阵质量往往不太好。随着迭代次数进一步增加，RMSE之和下降的速度明显变缓，但总体仍是下降，说明单应性矩阵的质量在进一步提升，当遍历完所有同名点对后便可获得RMSE之和最小时基准图像与待配准图像之间的最优映射关系，即单应性矩阵。

获得基准图像与待配准图像之间的最优单应性矩阵后，利用单应性矩阵对待配准图像进行重采样和插值运算，生成分辨率与基准图像一致的配准图像。本部分仍将网通卫星图像的波段0作为基准图像，波段1～7作为待配准图像，通过之前部分获得的基准图像与待配准图像间最优映射关系对波段1～7的图像进行重采样插值运算，生成与基准图像波段0同样尺寸的配准结果图。限于篇幅，图11～图14分别展示波段0-1、波段0-2、波段0-4和波段0-7的图像配准结果图与基准图像制成的棋盘图。

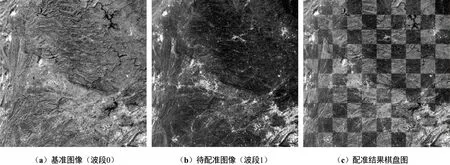
图11 波段0与波段1的图像配准结果Fig.11 Image registration results of band 0 and band 1

图12 波段0与波段2的图像配准结果Fig.12 Image registration results of band 0 and band 2

图13 波段0与波段4的图像配准结果Fig.13 Image registration results of band 0 and band 4

图14 波段0与波段7的图像配准结果Fig.14 Image registration results of band 0 and band 7

同样，本部分仍将之前高分二号的全色图像作为基准图像，使用得到的最优单应性矩阵对多光谱的波段1～波段3图像进行重采样和插值计算，生成与全色图像尺寸一致的配准结果图，配准结果棋盘图如图15～图17所示。从配准结果棋盘图可以看出，虽然待配准图像与基准图像之间的辐射差异不尽相同，但通过迭代更新策略的SIFT算法均能实现良好的图像配准，进一步提升了SIFT算法在不同遥感图像配准场景下的鲁棒性。

图15 全色图像与多光谱波段1的图像配准结果Fig.15 Image registration results of panchromatic image and multi-spectral band 1

综上所述，实验结果表明，基于迭代更新策略的SIFT算法不仅可以得到基准图像与待配准图像之间的最优映射关系，实现高精度的图像配准，还进一步提升了SIFT算法应对不同遥感图像配准场景的鲁棒性。

4 结束语

本文提出一种基于迭代更新策略的SIFT算法用于遥感图像配准，该算法通过迭代更新求解基准图像与待配准图像之间的映射关系，即求解单应性矩阵，最后得到RMSE之和最小的单应性矩阵即基准图像与待配准图像间的最优映射关系矩阵。实验结果表明，基于迭代更新策略的SIFT算法不仅可以得到基准图像与待配准图像之间的最优映射关系矩阵，同时也进一步提升了SIFT算法在不同遥感图像配准场景下的鲁棒性。由于图像特征点提取的均匀性也会对图像配准的精度产生影响，以后将对本文算法进行改进和优化，提升特征点提取的均匀度，进一步提升图像配准的精度。