基于改进粒子群算法的无人机三维航迹规划

陈明强，李奇峰，冯树娟，徐开俊

(中国民用航空飞行学院 飞行技术学院，四川 广汉 618307)

0 引言

随着航空技术与智能技术的不断进步，无人机在各个领域都有着良好的应用前景。无人机航迹规划是实现无人机自主飞行的关键一步，得到了世界的广泛关注和研究，目前仍是研究热点之一。在考虑各种环境威胁和自身性能下，如何在当前环境中规划出一条最佳的飞行路径，是一项非常重要并复杂的任务[1-2]。

无人机航迹规划算法可以大致分为2类:传统规划算法和智能规划算法。传统规划算法包括A*算法[3]、快速扩展随机数算法[4]、人工势场算法[5]和概率图算法[6]等。智能规划算法包括遗传算法[7]、粒子群(Particle Swarm Optimization，PSO)算法、蚁群算法[8]、动态窗口算法[9]和灰狼优化算法[10]等。PSO算法[11]是一种仿生智能算法，基本原理是利用群体与个体之间的协作和信息共享，得到最优解，具有搜索速度快和收敛速度快的特点，但是具有容易产生早熟和陷入局部最优值的缺点。

刘科等[12]利用Dijkstra算法粗略求得最短路径后使用PSO算法和最小二乘法拟合出最优路径。该算法虽然规划出了最优路径，但是只能适用于威胁和空间较小的环境。Zeng等[13]提出了一种基于非齐次马尔可夫链和差分进化的PSO优化算法，用于智能机器人在环境中遇到障碍物时的路径规划。通过利用非齐次马尔可夫链将PSO速度更新方程从一种模式跳跃到另外一种模式，加快了收敛的速度，同时差分进化增强了粒子全局搜索的能力，但是计算非常复杂且规划路径不够平滑。罗阳阳等[14]提出了一种使用突变算子更新粒子位置的方法。在PSO算法迭代的过程中，使用突变算子使得算法能快速收敛并摆脱局部最优值。朱佳莹等[15]提出了PSO与蚁群算法相结合的路径规划算法，利用PSO算法优化蚁群算法初始信息素，再使用改进后的蚁群算法进行全局路径规划。2种算法结合后全局搜索能力得到了较大提升，并且迭代次数更少，但是算法拐点较多，导致规划路径多为折线，不利于运行在实际环境中。

本文针对PSO算法的缺点，提出了一种将PSO算法搜索空间由原始的笛卡尔坐标系改为球坐标系，使得PSO算法能直接与无人机自身性能相关联。同时引入天牛须(Beetle Antennae Search，BAS)算法，克服传统PSO算法易陷入早熟、收敛速度慢的特点。

1 目标函数

对于无人机航迹规划问题，目标函数是用来评估规划航迹的质量，多是由一系列的约束条件和优化条件组成，目标函数值越小时，得到的航迹质量越好。为了确定目标函数，必须要考虑所有可能影响规划航迹质量的因素，例如：航迹距离、飞行高度、障碍物限制和航迹平滑度等[16]。假设航迹是由n个航迹点组成，(xi,yi,zi)表示第i个航迹点的位置。

1.1 航迹距离

航迹长度是判断规划航迹质量的重要指标，考虑无人机的续航能力，规划航迹越短越有利于无人机的实际飞行，因此航迹成本函数为：

(1)

1.2 飞行高度

无人机飞行过程中受自身性能的影响和任务的需要，一般飞行高度限制在最低飞行高度和最高飞行高度之间，无人机航迹飞行高度成本函数定义为：

(2)

1.3 障碍物限制

无人机飞行时需要距离障碍物一定的距离，假设空间中存在圆柱体障碍物，障碍物数量为T，无人机距障碍物距离为d，障碍物半径为R，无人机尺寸为S，为了提升飞行时的安全，设定碰撞危险区距离为D，障碍物模型如图1所示。

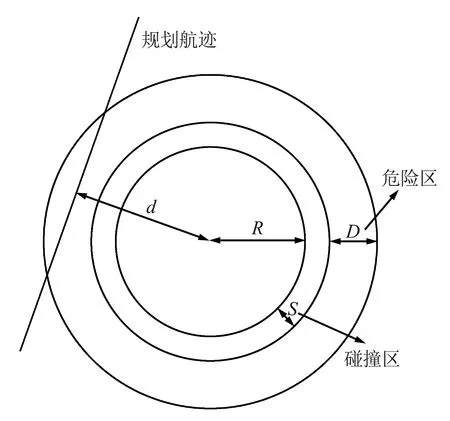
图1 障碍物模型Fig.1 Obstacle model

障碍物成本函数可以定义为：

(3)

(4)

1.4 航迹平滑度

规划航迹应该尽量少的偏航和高度切换，需要保持航迹的平滑，li表示2个航迹点之间的距离，式(5)和式(6)分别表示偏转角ai和俯仰角bi，航迹平滑度成本函数可以定义为式(7)：

(5)

(6)

(7)

1.5 总目标函数

无人机在执行任务的过程中需要考虑自身性能限制与地形性质，因此对无人机俯仰角、偏转角和飞行高度进行约束。以上约束条件参数均与成本函数参数有关，因此将飞行高度约束加入式(2)中，偏转角和俯仰角约束在SPSO算法中对粒子更新时已经做出了约束，所以无需对其设置额外的约束条件。

根据以上成本函数，可以构建无人机规划航迹的目标函数，由于无人机执行任务种类较多，并且每种任务所要求的航迹均不相同，所以定义wi，i=(1,2,3,4)分别为每种成本函数的系数，wi之间的关系如式(8)所示，根据任务的需求可以动态地调整权重，因此目标函数如式(9)所示：

(8)

F=w1Fl+w2Fa+w3Fo+w4Fs。

(9)

本文目标函数参数设定为：最高飞行高度hmax为300 m；最低飞行高度hmin为20 m；无人机尺寸S为2 m；危险区距离D为20 m；w1为0.4；w2，w3和w4均为0.2。

2 改进PSO算法设计

2.1 SPSO算法

PSO算法是由Kennedy和Russell提出，是基于鸟群和鱼群聚集行为的启发式优化算法。PSO算法具有认知和社会一致性，根据这2个特性，可以使得PSO中的粒子根据自己的经验和种群的经验自行搜索求解，从而摆脱了原始的进化算子。与其他的启发式算法相比，PSO算法对初始条件和目标函数的变化并不敏感，能够在适应多种环境的同时使用少量的参数，在较短的时间内获得具有收敛的全局解。

为了满足无人机飞行的实际条件，在规划无人机航迹的过程中应当考虑无人机的性能参数。在传统的PSO坐标下，通常需要根据无人机最大偏转角和俯仰角在目标函数设置约束条件。而SPSO将粒子的搜索空间由笛卡尔坐标系转换到球坐标系，在球坐标系(ρ,θ,φ)下，ρ表示航迹段的距离，θ表示俯仰角，φ表示偏转角，PSO的搜索空间可以与无人机偏转角和俯仰角之间产生相互关系，不仅增加了规划航迹的安全性也对无人机偏转角和俯仰角进行了约束。

在SPSO下，粒子i对应D维向量的一条航迹，每个向量代表了从一个航迹点到另一个航迹点的移动，粒子位置Ωi表示为Ωi=(Ωi1,Ωi2,…,ΩiD)，其中Ωij表示为(ρij,θij,φij)，速度ΔΩi可以表示为ΔΩi=(ΔΩi1,ΔΩi2,…,ΔΩiD),其中ΔΩij表示为(Δρij,Δθij,Δφij)。

SPSO算法获取到粒子在球坐标下的坐标点后，需要根据目标函数来判定粒子质量，获得粒子个体最优位置Pb和全局最佳位置Gb。因此，需要将粒子位置Ωi映射到笛卡尔坐标系下粒子位置Xi，Xi=(Xi1,Xi2,…,XiD),其中Xij表示为(xij,yij,zij)，粒子在笛卡尔坐标系下的更新方式为：

(10)

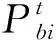
(11)

(12)

SPSO迭代过程中位置和速度更新公式为：

(13)

(14)

式中，w为惯性权重；C1和C2分别表示个体学习因子和群体学习因子；r1和r2均为0～1的均匀随机数。

2.2 BAS算法

BAS算法[17]是一种生物启发式优化算法，与PSO算法都是基于不断更新迭代获得最优解，但BAS算法是基于个体求解而非群体。BAS算法的优点在于算法复杂度低，只需要少量参数就能求解最优解[18]。

BAS算法是根据天牛的觅食行为而建立，将食物位置定义为最优解位置，食物的气味在空间中每个位置的浓度不同，将气味浓度定义为目标函数，当天牛的2根触须获取食物气味浓度存在差别时，其会随着气味浓度高的一侧移动，直至目标点，这样就可以建立起数学模型。

对于多维优化问题，首先需要确定天牛2根触须的坐标和触须之间的距离，其基本模型如图2所示，x表示天牛位置，xl表示左须坐标，xr表示右须坐标，d表示两须之间的距离。算法基本步骤如下：

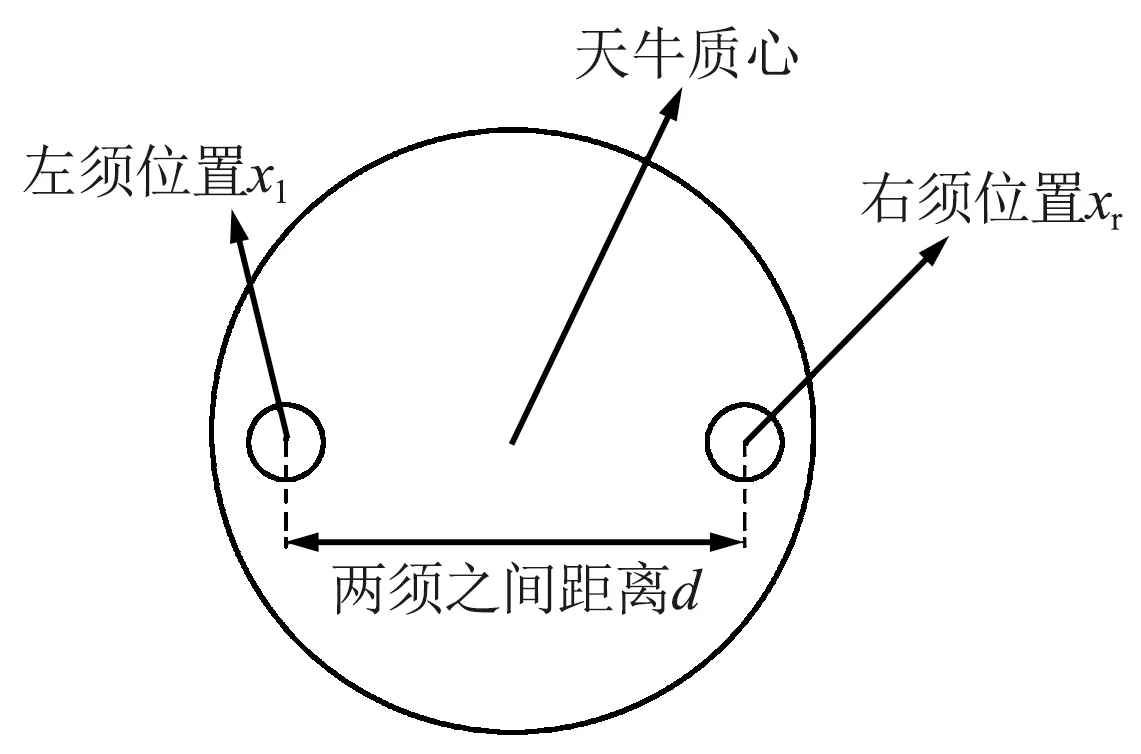
图2 天牛模型Fig.2 Beetle model

① 根据式(15)给出的归一化随机向量确定天牛个体的朝向：

(15)

式中，k代表待优化问题维数。

② 更新第t次迭代天牛左右须位置：

(16)

③ 获取到的天牛左右须位置后，计算目标函数值，分别用F(xl)和F(xr)表示左须和右须的目标函数值，根据天牛两须探测到的浓度差异决定下一步移动方向。

④ 迭代更新天牛位置：

xt+1=xt+δtbsign(F(xr)-F(xl))，

(17)

式中，δt为第t次迭代时天牛向下一个方向移动的步长；sign为符号函数。

⑤ 更新步长：

δt+1=ηδδt，

(18)

式中，ηδ表示步长衰减系数。

⑥ 判断是否可以终止迭代，如不满足，则回到步骤③，直至满足迭代终止条件，跳出迭代。

2.3 SPSO与BAS算法相结合

PSO算法着重于群体对单个粒子的影响，所以具有很强的全局寻优能力，但是也很容易陷入局部最优解，当粒子均趋向于全局最优解时，可能失去粒子的多样性。而BAS算法是只考虑个体，不考虑群体的影响，因此本文将PSO算法与BAS算法相结合，提出一种基于BAS算法的SPSO优化算法，在每一次迭代的过程中，利用BAS算法对环境空间进行判断，有利于跳出局部最优解，使得规划路径更加合理。

改进的算法将每个粒子也看作一个天牛，其整体步骤和PSO算法相似，在对粒子位置和速度进行更新的过程中加入BAS算法，改进后算法粒子的速度和位置更新公式为：

C3r3δtbsign(f(xr)-f(xl))，

(19)

(20)

改进后的算法，根据PSO算法的速度影响因子和BAS算法步长和触须的思想得到新的位置，算法的具体流程为：

① 初始化PSO参数，设置粒子维度D,学习因子c1，c2和c3，惯性权重W，以及天牛须两须距离d0。

② 随机化粒子初始位置和速度，并且计算适应度函数，使用初始化的位置作为个体最优解Pb，得到全局最优解Gb。

③ 按照式(16)计算天牛左右须位置，并且计算左右须位置的适应度函数，利用式(19)和式(20)更新粒子位置和速度。

④ 计算更新后粒子的适应度函数，更新粒子个体最优值、全局最优值和天牛须步长。

⑤ 判断是否满足终止条件，如满足，则输出最优值；否则，回到步骤③，继续迭代。

3 仿真分析

3.1 实验环境设置

为了验证改进算法的有效性，在Matlab环境下对无人机路径规划进行仿真建模。设计了2种仿真环境：一种环境中只有圆柱形障碍物，对应于地形较为平坦的城市环境；另一种环境是在第1种环境中加上了真实的地形数据，对应于地形较复杂的山区[19]。真实地形数据根据数字高程地图(Digital Elevation Model，DEM)获得，本文DEM数据由ALOS PALSAR数据库得到，根据DEM得到高程点，将其均匀地离散化在1 000×1 000的坐标空间中。

DEM数据选择31°04′56″N～31°11′37″N，103°50′58″E～103°57′47″E，离散在坐标空间后用x轴表示东经，x∈[0,1 000]，y轴表示北纬，y∈[0,1 000]，z轴表示高度，为每一个坐标点的真实高度。在环境1中设置起点为(330,40,50)，终点为(780,800,200)。环境2中设置起点为(1,1,50)，终点为(800,900,200)。

3.2 算法参数设置

SPSO算法参数设置为：最大迭代次数为300，粒子维数为10，惯性权重为1，自我认知和社会认知均为1.5。BAS算法参数设置为：天牛两须宽度为1，初始步长为0.1，天牛须认知为1.2，步长衰减系数为0.95。

3.3 仿真分析

本文分别采用标准PSO，SPSO和天牛须球坐标粒子群(BSPSO)三种算法对无人机航迹规划进行仿真验证，得到的仿真结果如表1和图3～图5所示。表1中所示数据是在环境1和环境2下分别运行10次所得到的仿真结果，其中数据为求得的平均值。图3是在仿真环境1中规划的航迹图，图4是在仿真环境2中规划的航迹图，图5是目标函数变化曲线图。

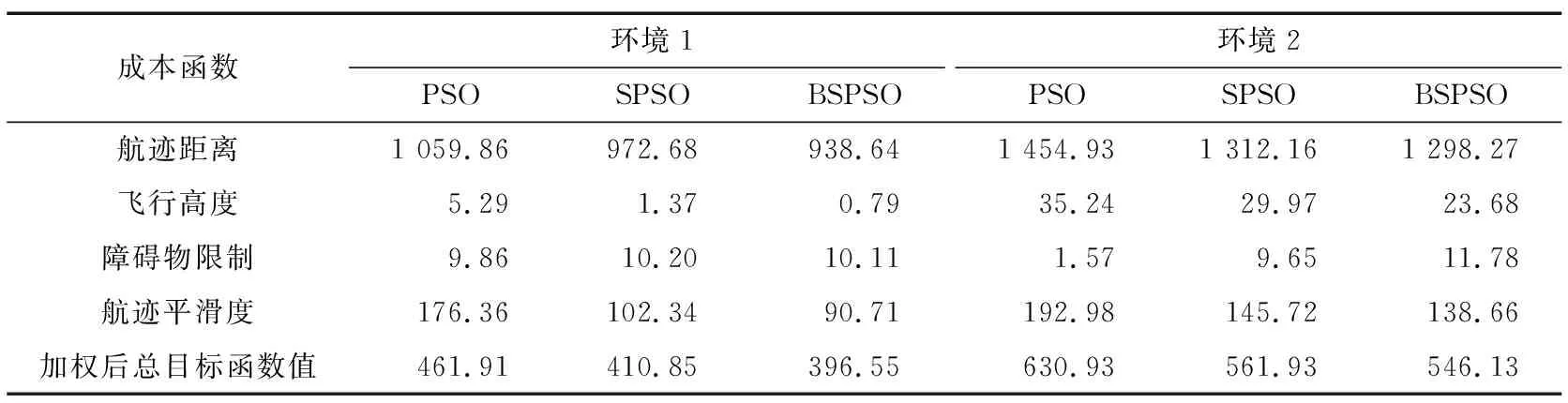
表1 3种算法在2种环境中的仿真结果对比Tab.1 Comparison of simulation results of three algorithms in two environments

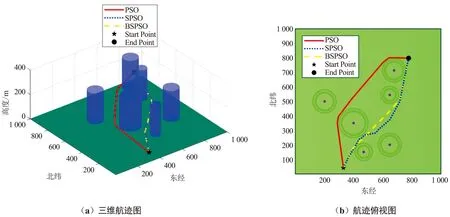
图3 仿真环境1规划航迹Fig.3 The planned trajectory in simulation environment 1

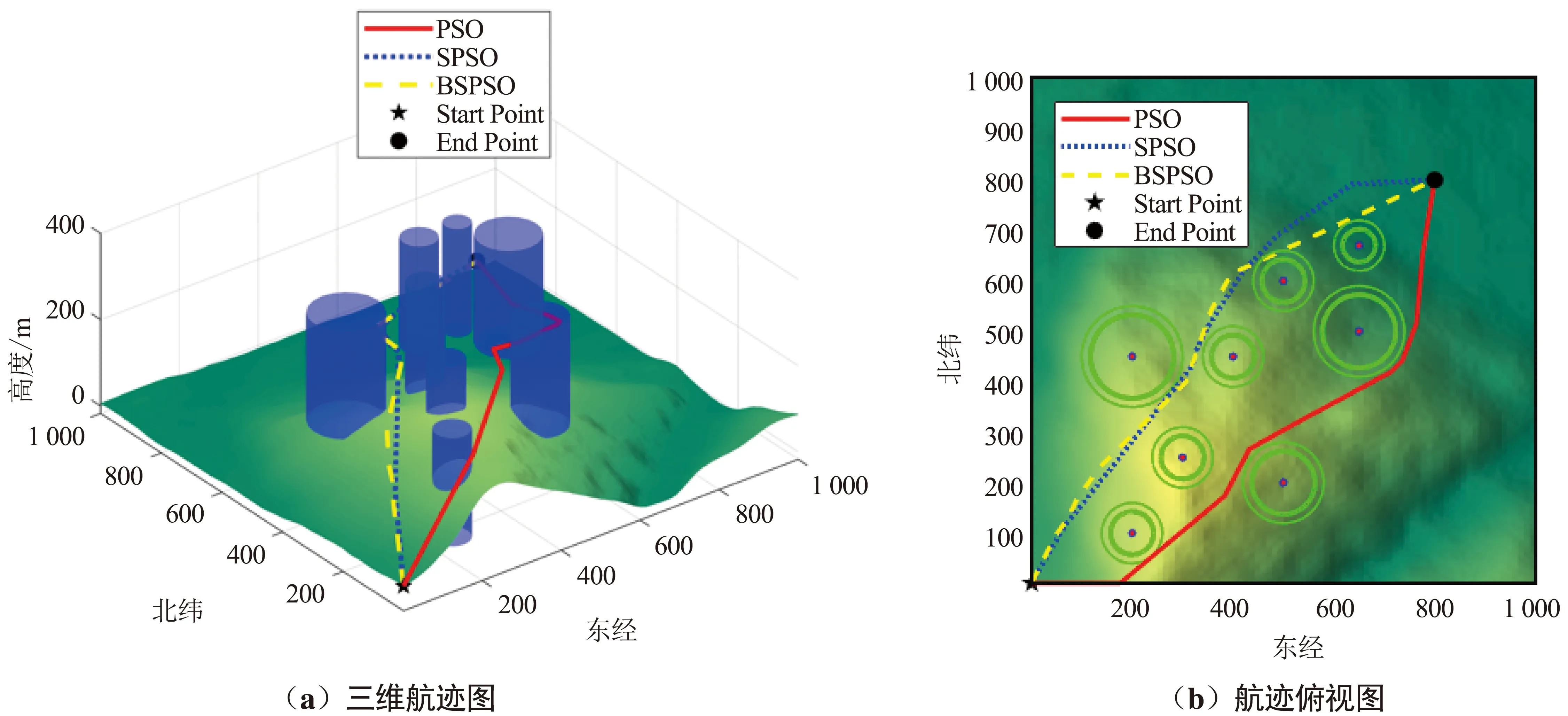
图4 仿真环境2规划航迹Fig.4 The planned trajectory in simulation environment 2

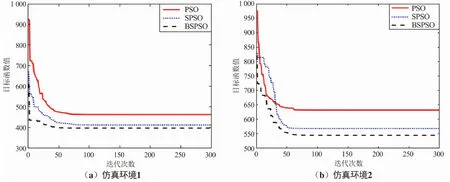
图5 目标函数曲线变化Fig.5 Change of the objective function curve

环境1为不带地形数据的简单环境，根据图3和表1可知，BSPSO规划的航迹长度明显低于PSO和SPSO，其航迹长度相比PSO和SPSO缩短了11.43%和3.5%。航迹平滑度BSPSO相比PSO和SPSO下降了48.57%和11.36%。飞行高度和障碍物限制上，3种算法的差距均不大，在加权后对应的总目标函数值均可忽略不计。在障碍物限制上PSO优于SPSO和BSPSO，这是由于BSPSO规划出的最优路线需要穿过障碍物，会进入障碍物危险区，而PSO规划的航迹选择绕过障碍物，增加了航迹长度。结合所有因数，加权总目标函数值BSPSO比PSO和SPSO分别降低了14.15%和3.5%，BSPSO规划航迹为最优航迹。

环境2为带地形数据的复杂山区环境，根据图4和表1可知，BSPSO规划的航迹长度明显低于PSO和SPSO，其航迹长度相比PSO和SPSO缩短了10.77%和1.59%。航迹平滑度BSPSO相比PSO和SPSO下降了28.15%和4.83%，这表明BSPSO算法规划的航迹更加平滑，偏转和俯仰的次数更少或者变化角度越少。由于山区地形复杂，无人机机动次数越少，不仅有利于节约能耗也有利于飞行安全。在障碍物限制上PSO明显优于SPSO和BSPSO，还是因为BSPSO在确保相对安全的情况下穿过障碍物，牺牲了部分障碍物限制，降低航迹长度。结合所有因数，加权总目标函数值BSPSO比PSO和SPSO分别降低了13.44%和2.81%。因此，BSPSO算法规划航迹在复杂地形中可以与地形的变化保持一致，满足了山区等复杂地形的航迹规划要求并且规划航迹最优。

根据图5可知，3种算法的总目标函数随着迭代次数的增加都在减小，但是PSO和SPSO算法目标函数值均大于BSPSO算法目标函数值，显然PSO和SPSO算法规划的航迹不是最优航迹，均陷入了局部最优值。而改进后的算法具有跳出局部最优值的能力，是由于PSO算法更新后，不是直接进入下一轮的搜索，而是利用BAS算法的更新规则，使粒子不再盲目地按照当前速度向发现的全局最优点聚拢，从而增加了对全体极值的搜索，使得局部搜索能力得到增强。因此验证BAS算法能够帮助PSO算法跳出局部最优值，证明了改进后算法的有效性。

本文通过空间复杂度和时间复杂度分析改进后算法的复杂度。改进后的算法通过BAS算法更新了粒子，其只是将原有粒子替换，并未占用新的运算空间，因此空间复杂度并未增加。由3种算法在仿真环境2下多次运行后得到迭代总耗时的平均值可知，SPSO耗时最短为165 s，PSO耗时最长为186 s，这是由于SPSO能对无人机性能条件直接约束，减少了计算量，而BSPSO在SPSO的基础上引入了BAS算法，增加了一定的计算量，总耗时为178 s，但仍比PSO算法少。

4 结束语

本文考虑了无人机飞行航迹长度、飞行高度约束、障碍物约束和航迹平滑度约束，建立了无人机航迹规划模型。通过提出了一种SPSO算法结合BAS算法对航迹规划模型求解，将传统PSO的搜索空间从笛卡尔坐标系转换到球坐标系，利用球坐标系直接与无人机飞行航向角和俯仰角产生约束，同时结合BAS算法有助于帮助PSO算法跳出局部最优解，获得最优航迹。通过Matlab仿真将改进算法与SPSO和传统PSO算法进行仿真测试，测试结果表明改进后的算法具有更强的全局搜索能力，并且规划出的航迹更短、更平滑，提高了无人机规划航迹的质量。