结合正交补空间反向学习策略的自然计算方法
2023-03-06季伟东
黄 亮,张 军,季伟东
(哈尔滨师范大学 计算机科学与信息工程学院,哈尔滨 150025)
1 引 言
自然计算(Natural Computation)通常代指从自然中获取灵感而发展起来的算法,主要研究领域包括人工神经网络,群体智能,进化计算,人工免疫系统等[1].自然计算方法具有自学习、自组织和自适应的特点,在传统优化算法难以求解的各类复杂问题中发挥重要作用.例如将粒子群算法(Particle Swarm Optimization,PSO)用于电力系统经济调度问题以优化燃料成本[2],将差分进化算法用于光电精跟踪系统以提高收敛速度与辨识准确度[3],将遗传算法用于求解标签印刷车间的排产问题以提高加工效率[4],将蚁群算法用于求解带时间窗的车辆路径规划问题以优化物流配送效率[5]等.
各种自然计算方法均将候选解当作不同个体,并通过模拟不同的自然行为来设计候选解的迭代方式,以期找到问题的最优解.然而随着算法迭代进行,种群可能会陷入局部最优区域,导致算法效果变差.因次,设计有效策略使群体跳出局部极值区域仍是自然计算的重要研究方向.
针对自然计算陷入局部最优问题已提出许多优化策略,如将种群分组[6]或对种群数据增加变异偏置[7,8]来增加多样性,将易陷入局部极值的算法与全局搜索能力强的算法结合来增强搜索能力[9],其中反向学习相关研究较多.Wang[10]等人将反向学习策略及柯西变异算子应用于粒子群算法,提出了基于反向学习的粒子群算法(Opposition-based Particle Swarm Optimization,OPSO),算法在8个测试函数上相较原始PSO有所提升;在随后的研究中,Wang[11]等人改进反向位置的计算公式,扩大反向粒子搜索范围,实验结果表明改进算法在部分测试函数上表现优异.反向学习策略易于应用,可与多种算法结合.Zhou[12]等人将反向学习策略应用于竞争粒子群算法,在竞争过程中部分粒子利用反向学习更新位置;钱晓宇[13]等人由此启发,提出一种基于Solis&Wets局部搜索的反向学习竞争粒子群优化算法.So-Youn Park[14]等人将反向学习策略与Beta分布结合应用于差分进化以提高算法收敛速度与搜索能力;Yu[15]等人将反向学习策略应用于差分进化以解决多任务优化问题;Azam Asilian Bidgoli[16]等人基于反向学习差分进化提出一种二进制差分进化算法,解决多分类模型的特征选择问题.Verma[17]等人利用反向学习策略为萤火虫算法获得更好的初始种群并提高算法收敛速度;Yu[18]等人将反向学习策略应用于萤火虫算法以帮助个体跳出局部极值范围;周凌云[19]等人将正交实验设计与反向学习结合应用于萤火虫算法,利用正交设计寻找个体与反向个体最优的维度组合.Long[20]等人将随机反向学习策略应用于灰狼算法帮助种群跳出局部最优.王坚浩[21]等人用混沌反向学习策略初始化种群解,为鲸鱼优化算法全局搜索奠定多样性基础.以上反向学习策略均用粒子关于解空间中心的对称点作为反向解,缺少探索粒子当前位置正交空间的能力,增强种群多样性能力有限.
本文基于线性空间的正交补空间理论,提出一种新颖的反向学习策略,增强种群多样性使算法能够探索群体最优粒子的正交空间.本策略不依赖具体的算法操作,因而具有普适性.
2 基于正交补空间反向学习策略的自然计算方法
2.1 正交补空间
为了说明策略的思想,先引入正交补空间的定义及相应定理.
定义.设W是欧式空间V的子空间,记W⊥为一切与W中向量都正交的向量所成的集合,称为W在V中的正交补空间[22].
定理1.设W是欧式空间V的子空间,则V有直和分解V=W⊕W⊥[22].
依据定理1,任何欧式空间V都可以分解为1个属于此空间的子空间W及其正交补空间W⊥.设线性方程组对应矩阵记为Am×n,此矩阵的行向量生成的向量空间记为R(A),此线性方程组的解所组成的空间记为N(A),则R(A)与N(A)构成Rn的一对正交补空间.
例如,设有线性方程组:
(1)
其对应矩阵:
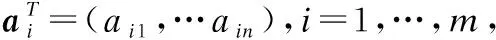
R(A)=c1a1+…+cmam,c1…cm∈R
(2)
R(A)共有r个线性无关向量.


(3)
其中c′1,c′2,…,c′m为a在式(2)中的相应值.由式(3)可得R(A)中的向量均正交于N(A)中的向量,特别的有r个R(A)中线性无关向量与n-r个N(A)中线性无关向量正交,则可得到n个线性无关的n维向量,并以此生成整个Rn空间,因此证得R(A)与N(A)构成Rn的一对正交补空间.
2.2 策略基本原理
本文提出一种反向学习策略,根据种群当前最优解,计算其正交补空间的基(basis),并以此生成新的个体.
设所求问题维度为D,将问题解空间记为RD,种群最优解记为gbest=(g1,g2,…,gD),对应正交补空间记为gbest⊥.建立方程组:
g1x1+g2x2+…+gDxD=0
(4)
可求得D-1个线性无关的解向量x1,x2…xD-1,应用Gram-Schmidt将解向量组正交单位化,得到gbest⊥内的正交单位化的解向量组u1,u2,…,uD-1,根据这组解能生成gbest⊥内的任意向量,且由u1,u2,…,uD-1,gbest可以生成RD内的任意向量,即可以生成任意候选解.
整个解空间RD的信息可分为两部分,一部分为gbest所在直线空间的信息,另一部分为gbest⊥空间信息,当群体陷入局部最优时,可通过组合两部分信息生成新个体以跳出局部极值范围.设:
s=g/G
(5)
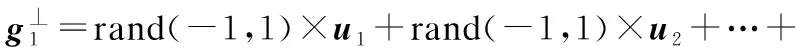
(6)
(7)
(8)
x⊥=(1-s)×g⊥+b×g,b~N(s,1)
(9)
其中g表示当前迭代次数,G表示总迭代次数,rand(-1,1)表示在[-1,1]上服从均匀分布的随机数,norm表示向量求模长运算,Mnorm表示gbest⊥空间内向量的最大模长,xmax、xmin分别表示解空间的取值上下限,g表示当前种群的最优解,由式(7)可知g⊥位于gbest⊥中,其模长服从均值从1至0变化的高斯分布.使用式(9)式来计算反向解,迭代初期,生成的反向解接近gbest⊥空间,随着迭代进行,反向解散布在整个空间中,充分探索潜在最优解,后期反向解靠近gbest所在空间.
2.3 正交补空间反向学习策略分析
为了说明策略有效性,设问题维数D=2,gbest=[2,2],解空间取值范围为[-5,5].则当s分别为0.1、0.5及0.9时,根据gbest计算其正交补空间的正交单位化的解向量组u1=[-0.707,0.707],根据公式(8)计算Mnorm=5,根据公式(6)、公式(7)生成gbest补空间内的随机个体,最后根据公式(9)计算反向解.生成的反向解(Opposition-Based Solution,OPS)分布如图1所示.
由图1可知当s值较小时,反向解多数分布在gbest⊥内,且模长较长,离gbest位置较远;当s值适中时,反向解分布在整个解空间,模长适中,充分探索空间中潜在的最优解;当s较大时,反向解多数分布在gbest所在直线空间,模长与gbest相似,充分探索gbest附近的空间.可见算法前期探索远离gbest的区域,种群多样性强,后期侧重开发gbest区域,寻找更高精度解的同时保持多样性.

图1 s为不同值时反向解分布Fig.1 Distribution of opposition-based solution with different s
2.4 算法的实现策略
本节给出算法具体实现步骤,算法流程图如图2所示.其伪代码如算法1所示:

图2 算法流程图Fig.2 Flow chart of algorithm
算法1.基于正交补空间反向学习策略的自然计算方法
步骤1.初始化种群数N,群体位置矩阵X等参数,计算个体对应适应度值f(X);
步骤2.forg=1 toG;
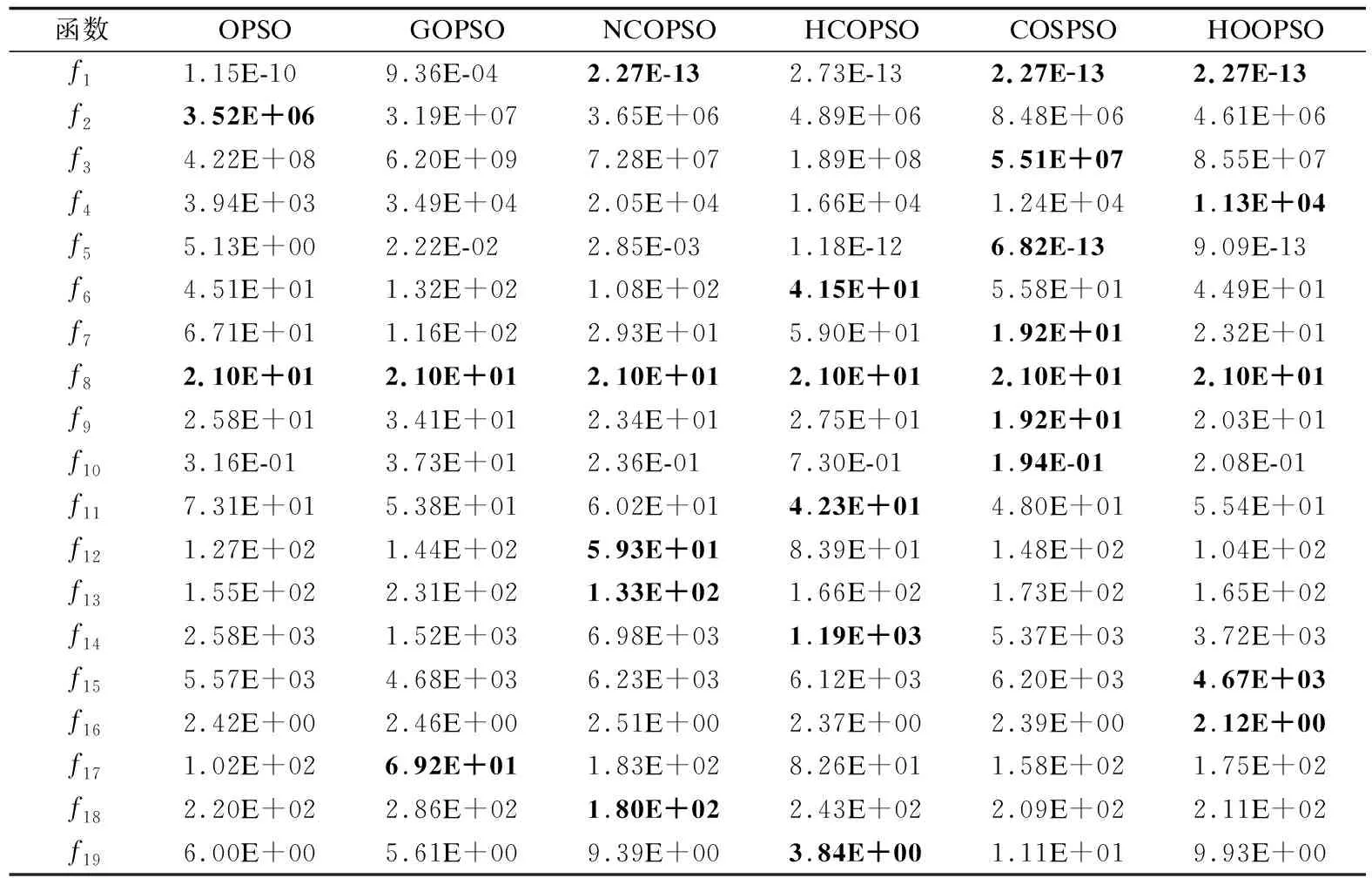
步骤3. ifrand 步骤4. 根据式(4)计算gbest⊥的正交单位化解向量组; 步骤5. 根据式(5)、(8)分别计算s、Mnorm; 步骤6. 根据式(6)、(7)、(9)计算N个当前gbest反向解,记为X⊥; 步骤7. 对X⊥中的N个反向解进行越界处理; 步骤8. fori=1 toN; 步骤12. end if; 步骤13. end for; 步骤14. else; 步骤15. 种群按照原始自然计算方法进化; 步骤16. end if; 步骤17.end for; 算法1中G表示种群总迭代次数,rand表示在[0,1]上服从均匀分布的随机数,Pc表示使用反向策略的概率,依据文献[10]的实验结果,Pc在0.3~0.5范围内取值可以提高反向算法寻优精度.为了更精确的对比原始反向策略与本文所提反向策略的性能差异,避免因超参数值的不同而导致的实验结果差异,采用原始反向策略的Pc值,即Pc=0.3,对越界个体采用吸收墙的处理方式,用解空间的边界值替换越界值.步骤4的具体实现依托仿真平台,以matlab环境为例,可用null函数计算方程组的正交单位化解向量组. 3.1.1 实验设置及结果分析 为了验证本文策略的有效性和普适性,将其分别应用到标准PSO与标准遗传算法(Genetic Algorithm,GA)中,记为正交补空间反向学习粒子群算法(Orthogonal Complementary Space Opposition-Based Learning Particle Swarm Optimization,OCOPSO)及正交补空间反向学习遗传算法(Orthogonal Complementary Space Opposition-Based Learning Genetic Algorithm,OCOGA).仿真平台为Windows10,MatlabR2020b. 将OCOPSO与PSO及OPSO[10]进行对比实验,比较两种反向策略的性能差异.参数设置:学习因子c1=c2=1.49618,惯性权重线性减小,ωmax=0.9,ωmin=0.4.将OCOGA与GA进行对比实验,参数设置:交叉概率为0.7,变异概率为0.05. 实验适应度函数为当前位置对应函数值.公共参数设置:种群数N=20,算法迭代次数G=1000,维数D=30.选取15个经典测试函数测试算法性能,其中f2~f6为多模函数,剩余函数为单模函数,因f13在30维上的最小值缺乏精准数据,暂定为-100作为衡量不同算法表现的标准,各函数表达式如表1所示.每个函数重复运行20次,取运行结果平均值与全局最小值的误差(mean)作为评价标准,计算20次运行结果的标准差(std),进行Friedman检验,结果如表2所示.碍于篇幅限制,选取算法在多模函数f2、f4、f5及单模函数f1、f8、f11上的收敛图比较算法性能,结果如图3所示. 表1 标准测试函数Table 1 Standard test functions 续表1 表2 算法在15个标准测试函数上优化结果Table 2 Algorithm optimization results of 16 standard test functions 图3 算法在6个函数上的收敛曲线Fig.3 Convergence curve for six functions of algorithm 由实验结果可知,OCOPSO相较PSO、OPSO而言,在f1-f5、f7-f13、f14函数上求得的解的精度较高.尤其对于f2、f8、f14,精度提高明显.OCOGA在除f5、f13以外的函数上寻得解的精度均高于标准GA,但精度提升相较PSO并不明显,这是因为GA本身并不易于陷入局部极值,反向策略对其性能提升有限.对于f2-f5多模函数,应用反向策略的算法寻得解的精度普遍高于原始算法,f6的全局极值点靠近解空间边界,且边界上存在许多局部极值点,OCOPSO前期大范围探索解空间,易陷入远离全局极值点的局部极值点,随着迭代进行探索范围减小,算法偏向开发当前群体最优点周边区域,因此最终找到局部极值.因此对多模函数而言,反向策略能帮助算法跳出局部极值区域继续搜寻全局最优解,而本文策略所生成的反向解相比OPSO生成的反向解更加多样化,能探索更大解空间范围,因而更有可能找到全局最优解.根据“没有免费午餐”定理,反向策略算法没能在所有类型函数上都寻得最高精度的解,但在大部分函数上其解的精度高于对比算法,且剩余函数上解的精度相近,表明本文所提策略的有效性. 从收敛曲线图3中可以看出,在相同的迭代次数时,OCOPSO不论在单模函数还是多模函数上均寻得精度高于PSO与OPSO的解,因此其收敛速度快于对比算法.尤其对于f2、f4、f8而言,对比算法收敛曲线在后期趋于平缓,而OCOPSO收敛曲线在后期仍有明显的下降趋势,说明正交补空间反向学习策略相比OPSO的反向学习策略改善种群多样性能力更强,找到最优解的概率更大.OCOGA在除f5外的函数上收敛速度均快于GA,其收敛曲线在f2上呈阶梯状下降,在f2、f4、f8上末端仍有下降趋势,表明本文策略具有较强的探索能力,能加快算法收敛速度,有效提高算法寻优效率. 为进一步验证本文策略在高维问题下的性能,分别设置问题维数D=100、200,对PSO、OPSO、OCOPSO、GA、OCOGA5种算法进行仿真实验.f7在高维度下计算适应度值溢出,因此选用剩余的14个函数作为测试函数,其他参数设置同上.取运行结果平均值与全局最小值的误差作为评价标准,如表3所示. 表3 算法在高维问题上优化结果Table 3 Algorithm optimization results of high dimension problem 由表3可知,在D=100、200时,OCOPSO与PSO、OPSO相比在除f6、f13、f15的测试函数上均取得精度最高的解,OCOGA与GA相比在除f6、f13、f15的测试函数上取得高精度解.两种问题维度下,OCOPSO在f1-f4、f8、f10、f11、f14上均寻得精度相似的最优解,说明本文策略能应用于高维问题求解,对其有较好的鲁棒性. 3.1.2 时间复杂度 运行时间是衡量算法性能的重要指标,且随问题维度增大而延长.因此,在D=100、200条件下,将结合本文策略的算法运行时间绘制成图,结果如图4所示.由图可知,两种维度下OCOPSO相较原始PSO算法运行时间增加约5%~10%;OPSO相较PSO运行时间增加越200%~250%;OCOGA相比GA运行时间增加约20%~70%,特别的当D=200时,在f9~f11上运行时间增加近100%.OPSO运行时间高的原因在于其柯西变异算子计算复杂,而本策略因计算正交反向解增加的时间在可接受范围内.结果表明相较GA,本策略更适用于PSO算法,并且能在略微增加运行时间的代价下寻得精度更高的解,具有较为优异的性能. 图4 不同维度下算法仿真时间对比Fig.4 Operational time of comparative algorithm with different dimension 为了进一步验证本文策略的性能,选用CEC13函数集作为测试函数[23],其中f1~f5为单模函数,f6~f20为多模函数,f21~f28为组合函数.选择4种结合反向学习策略的改进PSO作为对比算法,分别为OPSO[10]、GOPSO[11]、NCOPSO[24]、HCOPSO[25],其中OPSO及GOPSO为经典的基于反向学习策略的PSO算法,NCOPSO及HCOPSO是近年来提出的性能优异的反向学习PSO算法. 由于正交补空间反向学习策略后期开发能力不足及鲁棒性较差,为了弥补其缺点,将其与重心反向学习策略[26]及随机拓扑结构粒子群[27]结合.重心反向学习策略计算个体基于群体重心的反向解,将反向解限制在重心一定范围内,提高算法开发能力.在不清楚具体问题的情况下,随机拓扑粒子群往往优于固定拓扑粒子群[24],其鲁棒性较强.个体重心反向解[24]计算如下: (10) (11) 本文将结合两种反向学习策略的随机拓扑结构粒子群算法称为混合正交反向学习粒子群优化算法(Hybrid Orthogonal Opposition-Based Particle Swarm Optimization,HOOPSO),为了验证本文策略的有效性,将结合重心反向学习策略的随机拓扑结构粒子群算法作为对比算法,称为重心反向学习随机拓扑粒子群算法(Centroid Opposition-Based Learning Stochastic Topological Particle Swarm Optimization,COSPSO). 3.2.1 HOOPSO算法 (12) (13) (14) 其中l表示当前粒子的最优邻居粒子,其他符号含义同2.2节.随机拓扑PSO速度及位置更新公式如下: vid(t+1)=ωvid(t)+c1r1(pbestid-xid(t))+ (15) xid(t+1)=xid(t)+vid(t+1) (16) 其中vid(t)、xid(t+1)分别表示第i个粒子在第t、t+1次迭代时d维方向上的速度与位置大小,pbestid表示第i个粒子的历史最优位置在d维方向上的大小,r1、r2为服从[0,1]均匀分布的随机数,ω、c1、c2的设置同3.1节. HOOPSO先使用正交补空间反向学习策略生成反向解,若当前最优解没有提升,则使用重心反向策略,越界粒子采用吸收墙处理方式.算法迭代一次群体最优解没有提升时,重新选择个体邻居.其伪代码如算法2所示. 算法2.HOOPSO算法 步骤1.初始化种群数N,种群邻居矩阵L,位置矩阵X,速度矩阵V,计算个体对应适应度值f(X),flag=0; 步骤2.forg=1 toG; 步骤3. ifrand 步骤4. ifflag==0; 步骤5. fori=1 toN; 步骤7. end for; 步骤8. 对X⊥粒子进行越界处理; 步骤9. fori=1 toN; 步骤13. end if; 步骤14. end for; 步骤15. 更新相应的pbest; 步骤16. 若种群最优值没有提升,则flag=1; 步骤17. else; 步骤18. 根据式(10)、式(11)计算X*; 步骤19. 对X*的粒子进行越界处理; 步骤20. 计算f(X*); 步骤21. fori=1 toN; 步骤24. end if; 步骤25. end for; 步骤26. 更新相应的pbest; 步骤27. 若种群最优值没有提升,则flag=0; 步骤28. end if; 步骤29.else; 步骤30. 根据式(15)、式(16)式更新粒子的速度与位置; 步骤31. 对粒子进行越界处理; 步骤32. 计算适应度值,更新相应的pbest; 步骤33.end if; 步骤34. 更新相应的lbest; 步骤35. 若种群最优值无提升,则重构邻居矩阵L; 步骤36.end for; 3.2.2 实验结果与分析 参数设置:种群规模N=20,问题维度D=30,最大函数评估次数为100000,算法每轮计算20次函数值,因此迭代次数设为5000.其他参数设置同3.1节.所有算法运行25次,取25次均值与全局最小值的误差作为最终结果,GOPSO、NCOPSO、HCOPSO实验数据参照文献[25],使用Friedman检验分析所得结果. 实验结果如表4所示,将HOOPSO与OPSO、GOPSO、NCOPSO、HCOPSO进行对比,HOOPSO共在11个函数上寻得精度最高的解,其中包含单模函数f1、f4、f5,多模函数f7~f10、f15、f16,组合函数f23、f25,表明HOOPSO处理单模函数问题的能力更强,并且在多模及组合函数问题的优化性能上也有一定的竞争力.两两比较算法,HOOPSO相比OPSO、GOPSO、NCOPSO、HCOPSO分别在20、21、17、19个函数上寻得精度更高的解,Friedman检验表明HOOPSO具有最强的性能,应用正交补空间反向学习策略能有效提升算法寻优能力. 表4 算法在CEC13上优化结果Table 4 Algorithm optimization results of CEC13 续表4 为了验证本文策略的有效性,将HOOPSO与没有应用正交补空间反向学习策略的COSPSO进行对比,前者在18个函数上解的精度更高.对于单模函数,两个算法均有3个函数寻得精度最高解,在15个多模函数实验结果中,有8个较高精度解为HOOPSO所得,表明正交补空间反向学习策略能部分提高算法在单模函数及多模函数上的性能.应用策略后的算法没能在所有多模函数上寻得精度最高的解,可能是因为本文策略侧重探索与群体最优解相距较远的解空间,若算法在前期就寻得全局最优区域,策略所生成的反向解远离最优区域,造成评估次数的浪费,导致算法性能下降.对于组合函数,HOOPSO在7个函数上寻得精度最高解,表明正交补空间反向学习策略适用于解决此类函数优化问题.Friedman检验分析显示HOOPSO所得秩均值较小,表明正交补空间反向学习策略能够有效提升算法性能. 本文提出了一种新颖的反向学习策略,根据种群最优粒子计算其正交补空间的一组基,并依此生成反向解,提高种群多样性并增加找到全局最优解的概率.将本文策略应用于PSO及GA并在经典测试函数上与原始算法对比,实验结果表明算法寻优精度与收敛速度均有提升,策略具有良好的普适性.将其与重心反向学习策略结合应用于随机拓扑粒子群算法并用CEC13函数集进行测试,通过实验结果与理论分析表明,应用本文策略能提高算法性能.然而该策略在算法迭代后期开发能力不足,后续研究将集中于提高其开发能力,并将其应用于其他自然计算方法.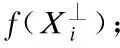


3 仿真实验与结果分析
3.1 经典函数测试实验





3.2 CEC13函数测试实验
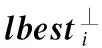
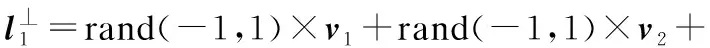
c2r2(lbestd-xid(t))



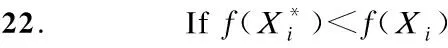
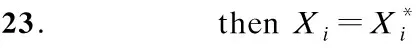

4 结 论
